基于视觉信息增强的服役燃机控制系统传感器故障分类方法研究
2023-09-26杨喜连王玉璋杨志鹏程侃如赵群飞
杨喜连, 王玉璋, 杨志鹏, 程侃如, 赵群飞
(1.上海交通大学 电子信息与电气工程学院, 上海 200240;2.上海交通大学 机械与动力工程学院, 上海 200240;3.上海发电设备成套设计研究院有限责任公司, 上海 200240)
随着全球能源消耗量的增加,能源与环境问题日益严重[1-2]。能源系统智能化能有效提升能源系统的调控水平,提高能源系统效率,是实现双碳双控目标行之有效的措施[3]。进行能源系统智能化时需要大量传感器在线实时检测能源系统的关键参数,从而实时感知能源系统中各关键部件的状态,实现能源系统的实时调控、健康评估和故障诊断[4-5]。传感器经常在高温、高压、高湿度、强磁场等恶劣环境下工作,因此传感器不可避免地会出现信号异常、老化等现象。状态监测通常分为4个步骤:异常检测、故障分类、故障隔离和故障缓解,故障检测是其中第1步。此外,故障检测还有助于实现智能控制。由此可见,开展燃机控制系统传感器故障诊断研究对于保障燃机的安全运行具有重要意义。
传感器采集的原始信号通常含有噪声,直接进行故障分类会导致效果不好,且原始数据的特征不明显。常用的基于数据的故障分类流程是先提取信号特征[6],然后再使用分类器。常用的提取信号特征的方法为信号分解[7-10],但针对小幅值故障信号及变工况的情况,通过信号分解得到的特征受限。在迁移学习中,基于数据的模型(如长短期记忆法、卷积神经网络)也可以用来提取特征进而进行故障分类,但小故障分类准确度会受到重构值准确度的影响[11]。
受计算机视觉中监督和无监督学习技术的启发[12],考虑将时间序列编码为图像,以允许基于机器视觉的算法识别、分类以及学习图像特征,充分利用卷积神经网络的优势。最近,研究人员试图从时间序列中构建不同的网络结构,用于视觉检查或设计距离的测量,如递归网络被用于分析来自复杂系统的时间序列的结构特性,时间序列的递归矩阵被解释为相关复杂网络的邻接矩阵,使用压缩距离来表示可扩展时间序列分类的递归图(Recurrence plot,RP)。构建加权邻接矩阵的另一种方法是从一阶马尔可夫矩阵中提取转换动态。尽管这些映射在不同的时间序列中表现出不同的拓扑特性,但由于没有精确的逆运算,这些拓扑特性与原始时间序列之间的关系仍不明确。
笔者利用格拉姆角和/差场以及马尔可夫转换场(MTF)将时间序列编码为图像,对包含5种典型故障(阶跃、短路、漂移、噪声、周期)的数据集上的时间序列进行二维图像转换,采用方向梯度直方图提取图像特征,再采用支持多分类的支持向量机对提取的图像特征进行分类。最后,通过混淆矩阵可视化分类结果来分析故障信号分类结果的误差来源。
1 燃机本体及问题定义
图1为各类状态传感器在燃机本体上的安装位置示意图。燃机系统中所安装的大量状态感知传感器大体上可以分为物理冗余和空间冗余2种类型。物理冗余是指在同一部件安装不同类型的传感器,由于安装在相同部件上,其具有一定的物理关系。空间冗余是指在同一空间内安装多个相同类型的传感器。传感器发生故障的原因主要有2个:一是燃机系统本身故障;二是传感元件发生故障。由于在燃机系统中燃烧室所处环境最恶劣,因此需要对指示燃烧状态的排气温度传感器(EGT)进行故障检测和分类。在涡轮出口安装多个传感器也会增加传感器故障的概率。
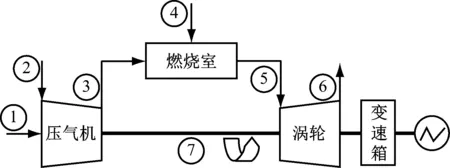
图1 各类状态传感器在燃机本体安装位置示意图
传感器故障分类的目标是根据传感器的历史观测值建模,然后及时对异常状态进行分类。记录的排气温度信号序列表示为时间序列X,目标是对故障信号分类问题进行建模。
(1)
式中:X为输入子序列;F为数据结构转换器;H为变换为二维图像后提取的图像描述子;G(ϑ)为带有参数ϑ的分类器;p为故障分类结果。
2 故障分类方法
真实燃机控制系统采集的传感器信号会伴有白噪声,故障信号的特征提取既要不受噪声干扰,同时又能反映出故障信号的特征,但很多工况下故障信号的幅值很小,较难区分其与变工况下正常信号的变化趋势。故障信号分类流程如图2所示。
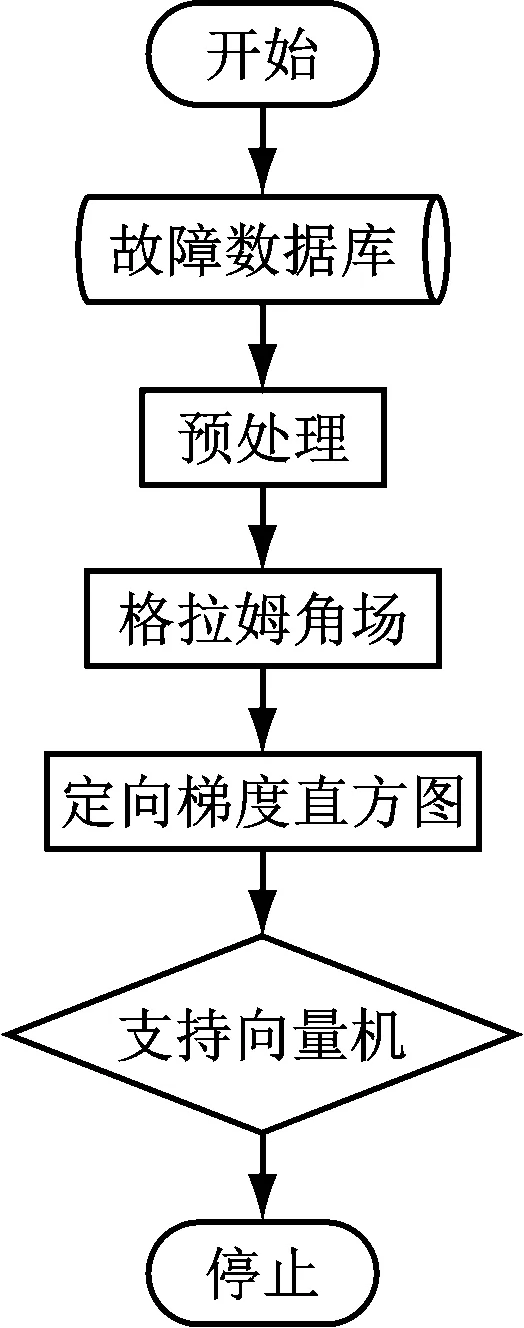
图2 故障信号分类流程
2.1 格拉姆角场(Gramian Angular Field,GAF)
将一段长为L的时间序列表示为X={xt}t=1,2,…,L,其中xt为时间序列中t时刻的值,然后将其缩放到统一的尺度区间[-1,1]或[0,1]中。
(2)
或
(3)
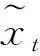
因此,可以将时间序列编码为角余弦,并将时间戳记为半径,使用式(4)在极坐标中表示重新缩放的时间序列。
(4)
式中:θ和r分别为极坐标中的角度和半径;ti为时间戳;N为常数因子,用于规范极坐标系的跨度。
随着时间的增加,时间序列对应的极坐标值在跨越圆上的不同角度点之间发生扭曲。式(4)的编码图有2个重要的性质。首先,极坐标编码图具有双射性质,这是由于θ∈[0,π]时cos(θ) 为单调函数。给定一个时间序列,所提出的映射在极坐标系中只产生一个结果,具有唯一的逆映射。其次,与笛卡尔坐标相反,极坐标保留绝对时间关系。
不同间隔的重新缩放数据具有不同的角度界限,继而在格拉姆角场中为分类任务提供不同的信息粒度。将重新缩放的时间序列转换至极坐标系后,可以通过考虑每个点之间的三角和/差并利用角度透视来识别不同时间间隔内的时间相关性。一段时间序列起始点对应的极坐标角度为θi和θj,格拉姆求和角场GS,(i,j)和格拉姆差分角场GD,(i,j)定义如下:
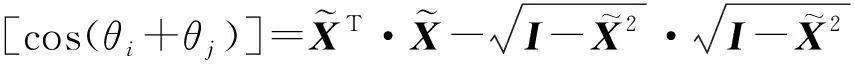
(5)
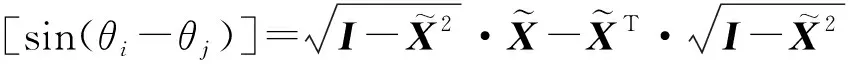
(6)
式中:I为单位行向量。
将时间序列转换至极坐标系后,将每个时间步的时间序列作为一维度量空间。由于G(i,j|(|i-j|=k))表示相对于时间间隔k的相对相关性,因此格拉姆角场具有时间相关性。主对角线Gi,i是k=0时的特例,其包含原始值/角度信息。然而,GAF矩阵很大,因为当原始时间序列的长度为L时,格拉姆矩阵的大小为L×L。为了减小GAF的矩阵大小,应用分段聚合方法来近似平滑时间序列,同时保留其趋势。生成 GAF 的完整过程如图3所示。
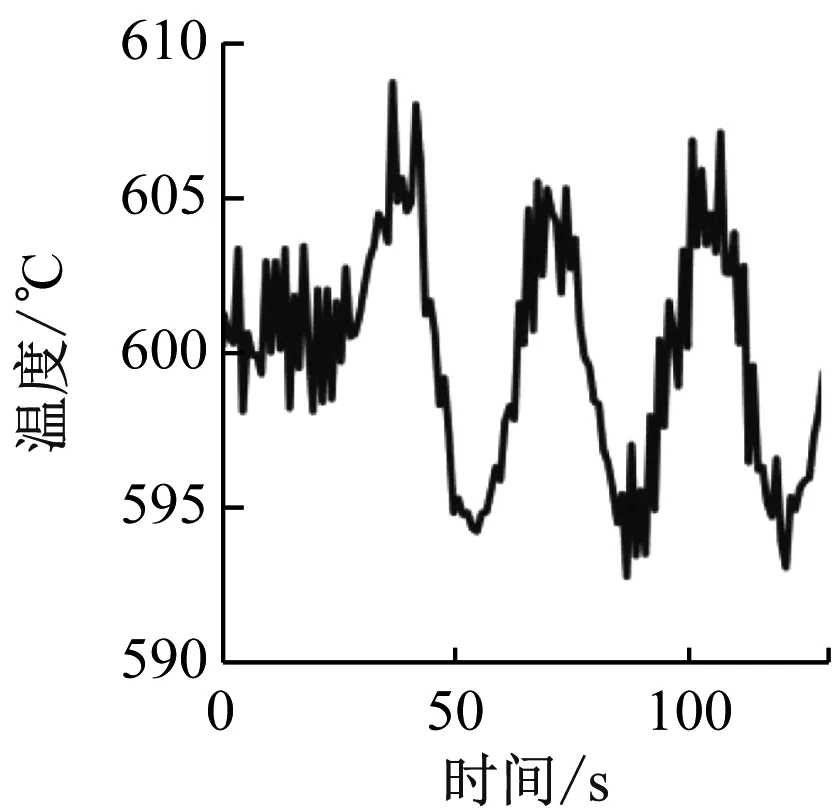
(a) 一维时间故障序列
2.2 方向梯度直方图
通过以下步骤计算方向梯度 (HOG) 的直方图:(1) 灰度化;(2) 全局图像归一化;(3) 计算每个像素的梯度(包含大小和方向);(4) 计算梯度直方图;(5) 跨块标准化,获取图像特征向量。步骤1是应用一个可选的全局图像归一化实现像素的均衡,旨在降低光照效果的影响,可使用伽马幂律压缩像素分布,计算像素的平方根或每个颜色通道的对数。步骤2是计算一阶图像梯度,捕捉边界、轮廓和纹理信息,同时进一步抵抗光照变化。计算梯度的变体方法还可能包括二阶图像导数,将像素的梯度充当原始条形检测器,用于捕获有用特征,如阶跃故障的格拉姆角场中的梯度变化,如图4所示。步骤3旨在产生一种对局部图像内容敏感的编码,同时其对噪声或外观的微小变化具有抵抗力,其主要目的是在本地汇集梯度方向信息。步骤4需计算归一化,采用局部单元组并在传递到下一阶段前对其整体响应进行对比归一化。归一化为照明、阴影和边缘对比度引入了更好的不变性,将归一化的块描述符称为HOG描述符。步骤5是从覆盖检测窗口的密集重叠网格的所有块中收集 HOG 描述符到组合特征向量中,以用于分类器的输入。

图4 短路故障下采用格拉姆角场变换得到二维图像后的灰度化图及对应的HOG
2.3 支持向量机
折页损失L为:
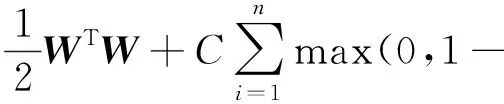
yi(WTφ(xi)+b))
(7)
式中:n为训练集的数据量;xi为输入数据;yi为标签数据;W和b分别为超平面的法向量和截距;C为调节系数;φ为核函数。
该分类估计器使用随机梯度下降 (SGD) 学习实现正则化线性模型,即每次估计各样本的损失梯度,且模型随着学习率的递减不断更新。SGD 允许通过部分拟合方法进行小批量在线学习。为使用默认学习率计划获得最佳结果,输入数据需具有零均值和单位方差。
3 结果与分析
以深圳某电厂的一台9F燃气轮机的运行数据作为实验数据,选取3个168小时段运行数据,每1 min采样一次,每段运行数据采集量为10 079个。由TimeSynth生成短路、阶跃、漂移、噪声、周期等故障信号,并将其叠加在真实运行数据上。
图5为小幅值故障信号的可视化结果,以检查格拉姆角场的纹理显示能力,可视化结果表明图像纹理质量可以接受。图5(a)为正常运行下的数据,从格拉姆角场中可以看出,原始信号有微小的负斜率。当施加微小的正漂移时,格拉姆角场正好变成更加均匀的分布场,如图5(d)所示。图5(b)为施加微小负阶跃后的曲线,对应的二维编码图也印证了负斜率的纹理特征。这说明格拉姆角场分布图可以放大微小信号的特征,将一维时序图转换为二维图后,原本不容易观察出的特征能够轻易地被发现。图5(c)为施加微小正阶跃的曲线,其变化与施加微小负阶跃的曲线正好相反。图5(e)为施加微小噪声故障后的曲线,可以看出,与正常信号相比,其所带噪声更大。图5(f)为施加微小周期故障后的曲线,其变化具有周期性。
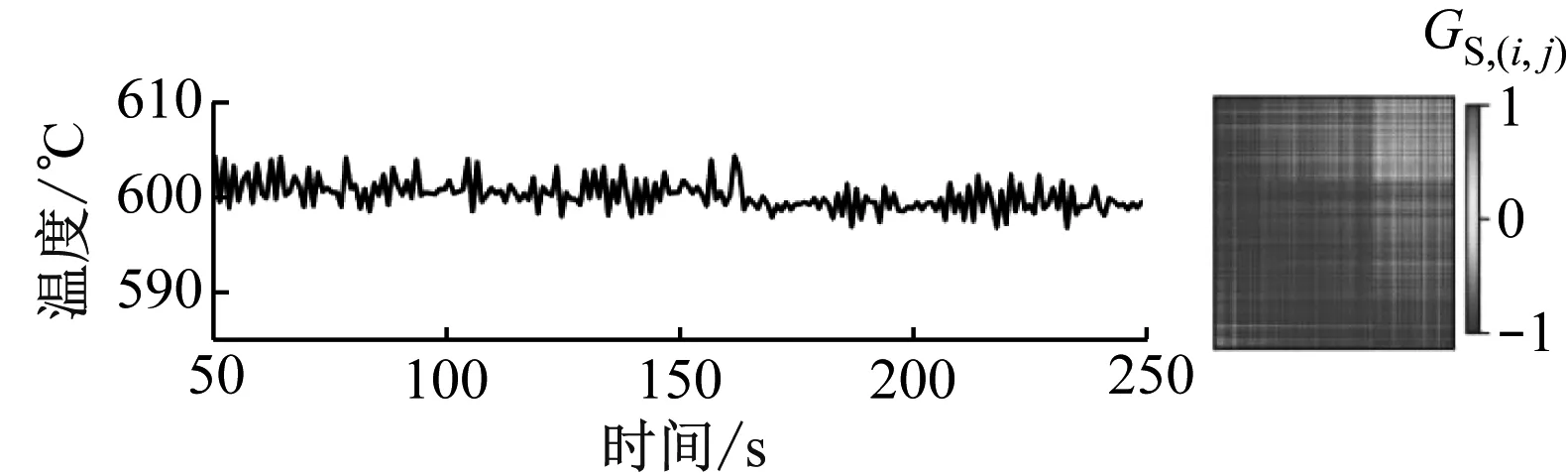
(a) 正常信号
结合图6和图7可以看出,随着故障幅值的增加,二维像素的颜色变深。其中,施加正阶跃和负阶跃后可视化结果区别不大。由图6和图7(a)可知,漂移故障与其他故障相比有比较明显的纹理区别,但是对于小漂移故障,GAF的纹理更明显,而马尔可夫转换场M(i,j)的纹理则与小噪声故障下的纹理相似。对于小噪声故障,MTF的纹理比GAF更丰富。在小噪声和小周期故障下GAF的纹理较相似。
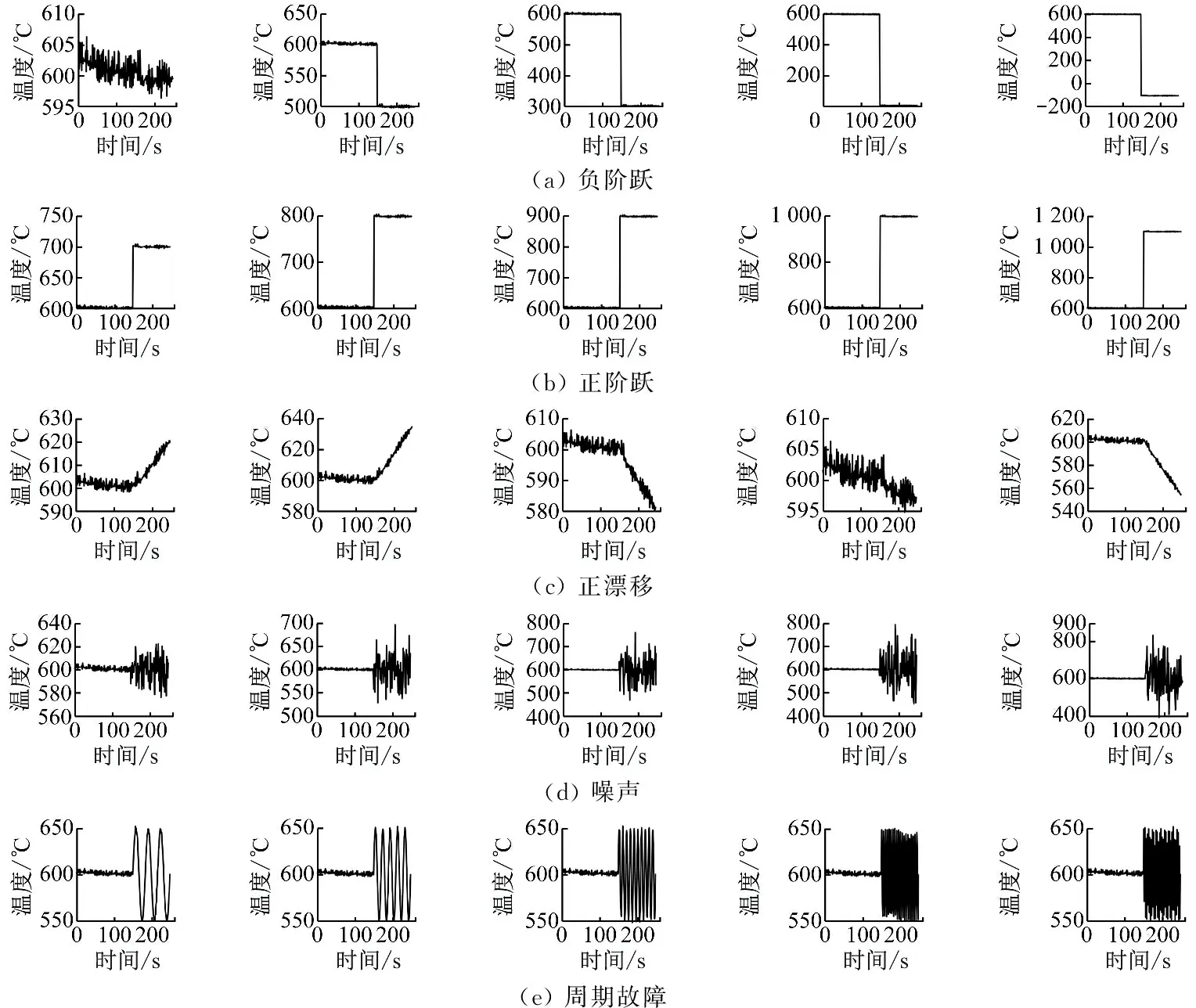
图6 大幅值故障下原始线框图

(a) 格拉姆角场GAF
在相同的故障数据集下对比了不同可视化方法的分类准确率及运行时间,如表1所示。该数据集包含5类故障信号的幅值情况。采用格拉姆求和角场和MTF时结果最好,分类准确率达到96.6%,但其分类混淆矩阵可视化结果并不完全一致。图8给出了基于格拉姆角场故障分类结果的混淆矩阵。其中,nt表示各类故障的数量,p表示某类故障数量与该类真实样本数量的比值。使用格拉姆求和角场将一维故障信号可视化后,其中21%的噪声故障被误检测为周期故障。图9给出了基于马尔可夫转换场故障分类结果的混淆矩阵,使用MTF将一维故障信号可视化后,12%的漂移故障被误检测为噪声故障。图8和图9中的数字1~5均分别代表漂移、噪声、周期、短路、阶跃。

表1 不同可视化方法下的故障分类准确率及运行时间

(a) nt
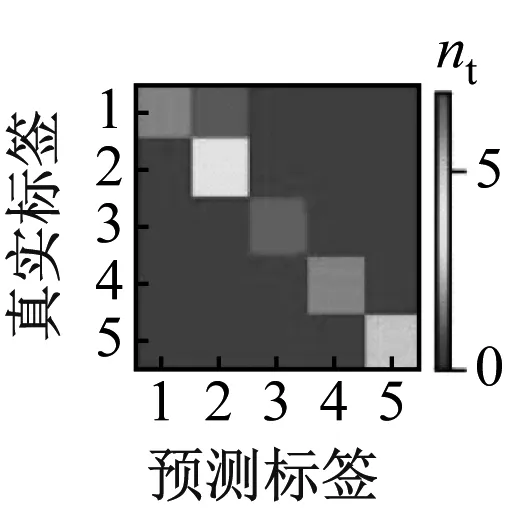
(a) nt
4 结 论
(1) 将幅值较小、不易被检测的时序数据转换为可视化图像后,图像纹理特征明显,有利于特征提取。
(2) 所提出的传感器故障诊断和分类方法的准确率能达到96.6%,格拉姆求和角场与马尔可夫转换场的故障分类准确率相同,但由于其特性不同,两者误差的来源也不相同。
