数形结合，探索数概念的一致性——《真分数、假分数和带分数》教学实践与思考

○衡水市教育科学研究所 赵红生

课前思考：

冀教版小学数学三年级下册学生初步认识分数，定义为：把一个物体或一个图形看作单位“1”平均分成若干份，表示这样的一份或几份的数；四年级下册分数的内涵有所扩充，“一捆小棒”“一筐西红柿”“一束鲜花”也可以描述成一个整体用单位“1”表示。在此基础上，五年级下册教材安排了《真分数、假分数和带分数》的教学。

本课的教学是仅仅停留于观察比较分子和分母的大小，将分数分为真分数和假分数两类，还是需要把分数意义进一步拓展和延伸，让学生准确把握真分数和假分数的本质特征，体会数的一致性呢？答案无疑是后者。

基于对教材的研读和学生对分数的认知，把本课学习目标定为：结合具体图形和分苹果的事例、分数与除法的关系，经历真分数、假分数的产生过程；学生理解真分数、假分数、带分数的意义，利用数形结合探索三种数之间的关系；感受真分数、假分数都是分数单位累加产生的，逐步养成利用几何直观解决问题的意识。

课堂展示：

一、激活经验，提出问题

课件出示：把5 个苹果平均分给4 个小朋友，每人分几个？

生：5÷4=1.25（个）。

生：5÷4=1（个）……1（个）。

师：对，这是假分数。看到这个分数，你们有什么想法？

生：分子怎么比分母大？

生：把一个苹果平均分成4 份，最多取4 份，多出的1 份怎么取呢？

二、自主探究，发现本质

1.假分数的产生。

师：每个苹果都太大了，一个人根本吃不完，除了“每个人分一个再分余下的”之外，还有别的分法吗？

生：把5 个苹果都平均分成4 份，每人得到5小份。

教师示范画一个圆代替苹果，平均分成4 份，取其中的1 份，板书：（1 个），并强调单位“1”是一个苹果；接着分第2 个苹果，平均分成4 份，取其中的1 份，这时每人共分得2 个，板书：）。

师：请学生来分剩下的苹果。

生：把第3 个苹果平均分成4 份，取其中的1份，每人共分得3 个

生：把第4 个苹果平均分成4 份，取其中的1份，每人共分得4 个

生：把第5 个苹果平均分成4 份，取其中的1份，每人共分得5 个

生：把每个苹果都平均分成4 份，取其中的1份，每人共分得5 个

师：如果平均分6 个苹果呢？

2.揭示真分数和假分数的意义。

师：我们一起数一数刚刚分得的这些分数，你能给它们分分类吗？

学生觉得这种分法有道理，但与数学的规定不同。教师按照数学上的规定圈出真分数（）和假分数（），让学生说一说真分数和假分数的意义，并举几个假分数的例子。

师：仔细观察这些真分数和假分数，它们有什么共同点？

师：真分数和假分数都是分数单位累加产生的。关于假分数，你想了解它的哪些知识呢？

生：为什么叫假分数？

生：假分数与带分数、真分数有什么联系？

三、数形结合，构建联系

活动要求：先想一想，再写一写，也可以画一画，让别人一眼就能明白你的想法。教师选出有代表性的作品进行展示。

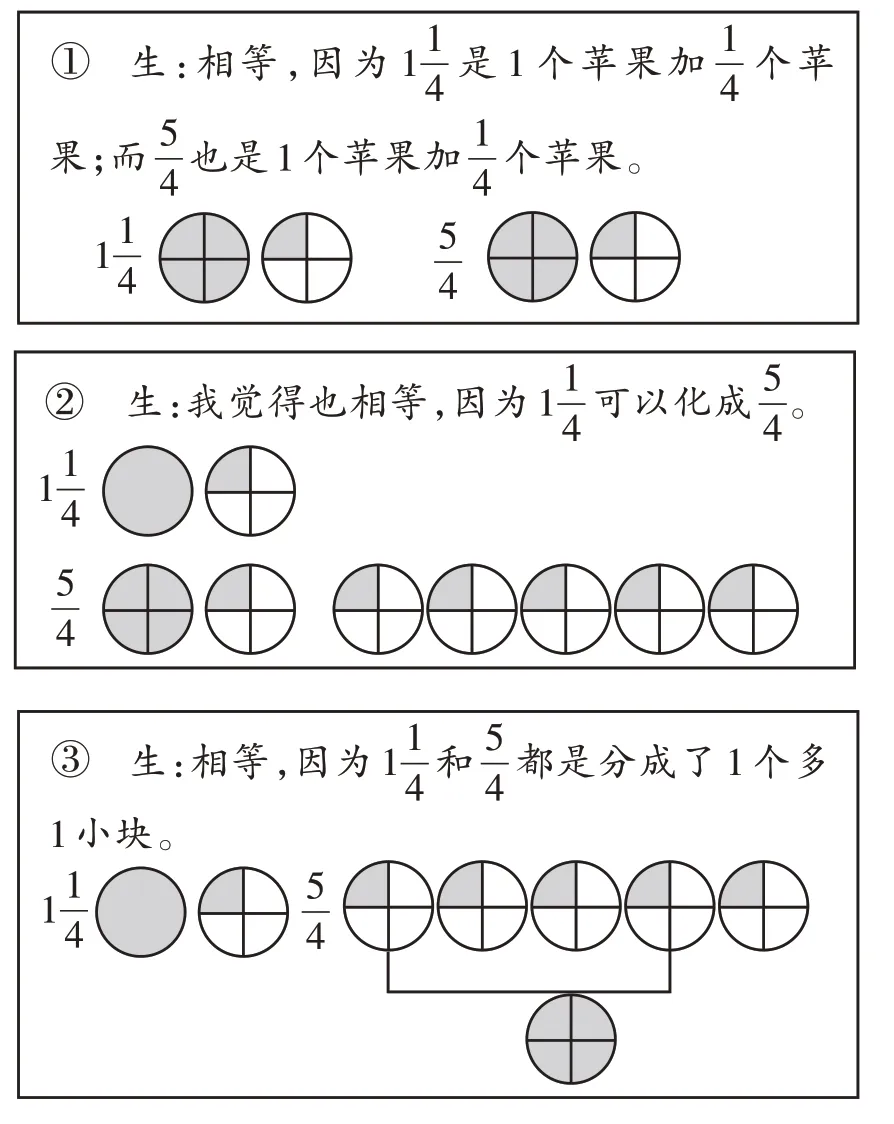
师：你能看懂哪个，请说一说。

2.为什么叫假分数？

师：如果把苹果增加到8 个、9 个呢？结果又该怎样表示？请写在第二个框里，完成后，同桌说一说结果是怎么得到的。

教师选出有代表性的作品进行展示（如图），并让学生说明理由。

师：仔细观察这些答案，你们知道为什么叫假分数了吗？

生：假分数变来变去的，怪不得叫它假分数呢！

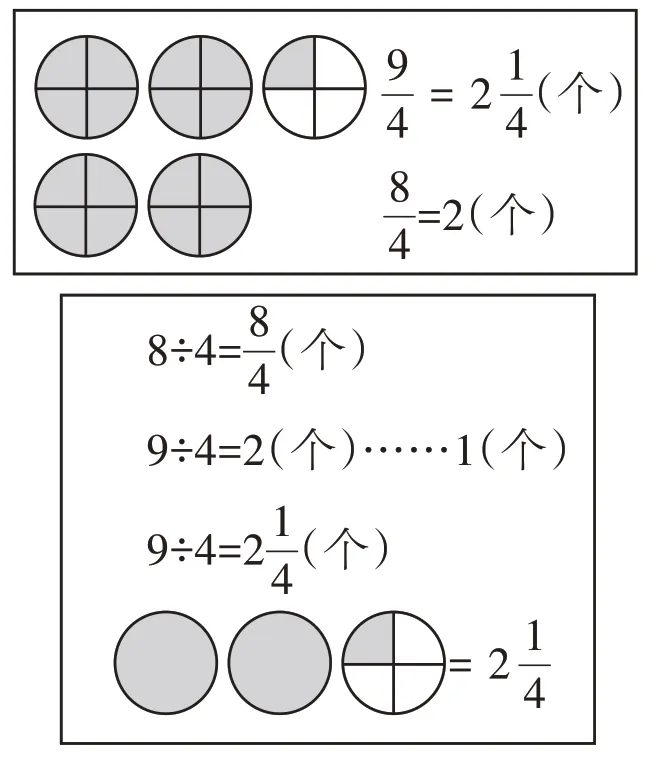
师：说得对，所以假分数既包含分子比分母大的分数，还包含分子和分母相等的分数。

师：大家仔细观察（如图），你们有什么想说的？

生：不是，带分数应该是由整数和真分数合成的。

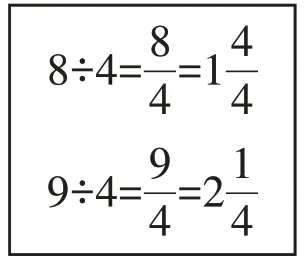
教学反思：

对多数学生而言，理解假分数的意义是本课的重难点。假分数的出现，无疑刷新了学生对分数的认知。

1.感悟数的概念本质上的一致性。

分数单位就是分数的计数单位，它随着单位“1”被平均分成的份数的变化而变化。学生在已有计数经验的基础上，明白了“几个几分之一就是几分之几”。分数单位不断地累加凸显了真分数的局限性与引入假分数的现实意义，由此帮助学生建立新的认知，无论是整数、小数，还是分数，都是计数单位的累加，以及数的概念本质上的一致性。

2.通过数形结合建立分数间的联系。

认识了假分数，学生自然也接受了利用分数与除法的关系得到的结果，但是它与带分数之间有怎样的关系呢？这又是困扰学生的一个问题。于是教师提出了“相 等 吗”“如 果把苹果增加到8 个、9 个呢”这些关键问题，学生利用数形结合的多样表达诠释了分数之间的相等关系和假分数的概念，感受将复杂问题变直观和简单的过程，进一步培养了几何直观能力。