库水位降落与降雨耦合作用下鸡脑壳包滑坡变形分析

江俊杰，刘东泽，卢应发

（1. 湖北工业大学土木建筑与环境学院，湖北 武汉 430068； 2. 中冶武勘工程技术有限公司，湖北 武汉 430080）

0 引 言

自2003年三峡水库开始周期性蓄水以来，由于库区的地质条件被极大地改变，三峡库区沿岸产生大量涉水滑坡［1］，这些滑坡一旦发生大规模失稳，将对人民的生命财产安全造成巨大威胁［2］。

由于滑坡变形是一个复杂、作用机理不明确的过程，因此诸多学者对滑坡的变形情况与稳定性影响因素进行了研究，如唐军峰等［3］利用SEEP/W 软件对库水位升降和降雨进行模拟，并计算不同条件下的稳定性系数，以此来研究不同库水位波动速率及降雨强度作用下滑坡体的渗流特征和稳定性变化规律；曾刚等［4］采用Geo-studio 软件得到滑坡的安全系数变化规律。分析了在库水位变动和最危险库水位变动叠加降雨两种工况下滑坡的稳定性。谢林冲等［5］在滑坡的地表位移监测数据、库水位变动及降雨资料的基础上分析了滑坡的时空演化过程，并通过耦合分析确定了库水位下降和降雨是滑坡变形的关键因素。王乐等［6］根据非饱和渗流原理利用有限元软件对不同降雨类型联合库水位骤降情况下的滑坡稳定性进行分析。雷德鑫等［7］采用蒙特卡罗随机抽样法，分析了滑坡在不同环境下的稳定性，同时分析了滑坡的稳定性系数对滑体物理力学参数的敏感性。胡致远等［8］通过建立滑坡多滑带地质模型，来研究库水位联合降雨作用下滑坡的变形和稳定性。张夏冉等［9］采用极限平衡的定量计算与破坏概率的定性分析，分析了不同库水降速及不同降雨条件下的滑坡稳定性。肖先煊等［10］通过建立滑坡的地质力学模型，来分析滑坡体在降雨及库水位升降作用下滑体内水压力、土压力的变化规律及稳定性。

诸多研究表明库水位波动和降雨是三峡库区滑坡发生变形的主要诱因［11］。为分析库水位降落联合降雨耦合作用下的滑坡破坏机理，本研究以鸡脑壳包滑坡为例，通过建立二维、三维库水位联合降雨的耦合数值分析模型，分析滑坡在不同环境下的变形演变规律，同时建立滑坡变形破坏的数值预测模型，预测最危险情况下鸡脑壳包滑坡的变形特征，再采用Morgenstern-Prince 法计算不同库水位降速率、不同降雨强度及降雨历时组成的降雨过程对应的稳定系数，为三峡库区水位变化及降雨条件下沿岸滑坡的监测防治提供参考。

1 数值分析模型

1.1 工程概况

鸡脑壳包滑坡位于巫山县曲尺乡柑园村，长江干流长江左岸，滑坡前缘涉水，距三峡大坝141.30 km，滑坡体处于巫山县向斜南冀，附近无大的断层，裂隙不发育。

鸡脑壳包滑坡体长600 m，宽500 m，后缘高程355 m，滑坡前缘直抵长江河边，剪出口位于135 m 处，在库区蓄水水位以下，滑坡全貌如图1所示。整个滑坡以下伏基岩为滑床，左右两侧分别以沟谷、冲沟为界，呈横长形，滑坡中部和后缘稍陡，前缘较缓，平均坡度30°，坡向150°，后缘陡壁坡度35°，高10 m。滑坡体厚50 m，滑体面积30 万m2，体积1 500 万m3。

图1 鸡脑壳包滑坡全貌Fig.1 General view of Jinaokebao landslide

鸡脑壳包滑坡所处的巫山县年降雨分布图如图2 所示，其中强降雨主要集中在4 月份至10 月份，其余月份降雨相对较少。

图2 巫山县年降雨量Fig.2 Annual rainfall in Wushan County

1.2 计算参数

根据鸡脑壳包滑坡地勘资料确定计算相关参数，具体数值见表1，二维计算剖面的地质剖面图如图3所示。

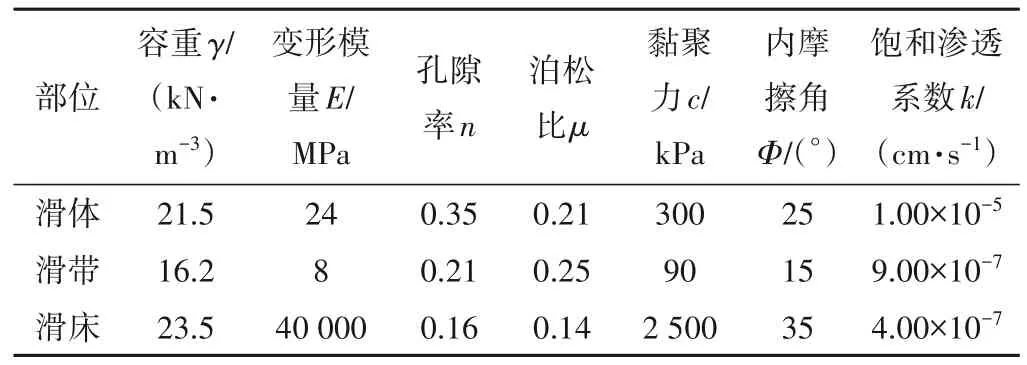
表1 鸡脑壳包滑坡数值计算参数取值表Tab.1 The value table of numerical calculation parameters of Jinaokebao landslide

图3 滑坡剖面图Fig.3 Landslide profile map

1.3 边界条件

降雨和库水位变化时滑坡渗流的边界条件如图4 所示，其中滑坡前缘库水浸没部分为水头边界。斜坡表面处降雨引起的入渗为流量边界，当降雨强度大于岩土体入渗速度时，边界流量值取岩土体入渗速度值，反之则取降雨强度值。模型底面和两侧为自由渗透边界且基岩的渗透性较小，可视为不渗透边界。

图4 边界条件示意图Fig.4 Schematic diagram of boundary conditions

1.4 计算模型

通过地质剖面建立二维计算模型，利用GEO-SLOPE 有限元软件对鸡脑壳包滑坡主纵剖面进行四边形单元网格剖分，节点数为8 130，单元数为8 035，网格图如图5所示。

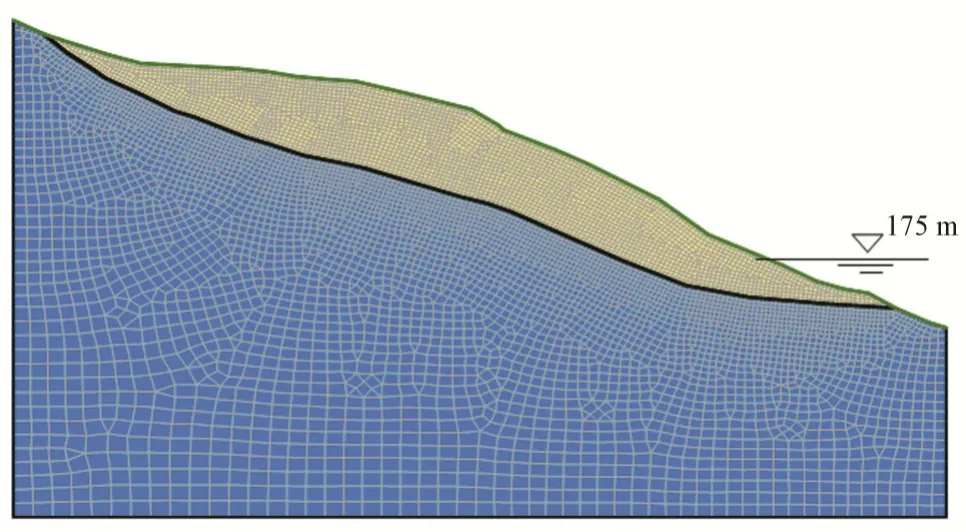
图5 二维计算网格模型图Fig.5 2D computational grid model diagram

根据鸡脑壳包滑坡的实际地貌特征建立思维三维数值计算模型，取值范围为分别平行、垂直长江水流方向886、850 m，模型底面高程为0 m，滑体、滑带、基岩均包含在计算域，该计算域剖分了36 864 个六面体单元，共计42 250 个节点，三维计算模型与网格如图6所示。

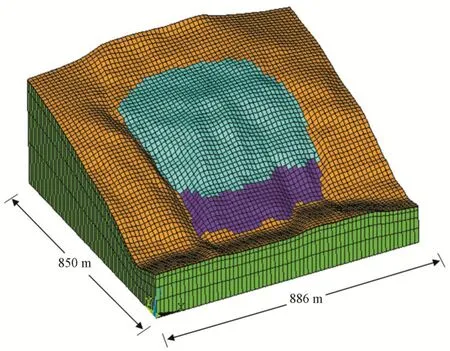
图6 三维计算网格模型图Fig.6 3D computational grid model diagram

1.5 工况设计

三峡工程全年水位调度图如图7 所示。其中6 月至9 月为汛期，此期间是强降雨的高发期，因此三峡库区为满足蓄洪要求，会将库水位从162 m 快速下降至145 m。而在10月至次年5月为非汛期，在此期间内降雨量相对较少，库水位变成为缓慢消落方式，水库水位从175 m缓慢下降至145 m。所以在计算中考虑快慢两种消落方式。

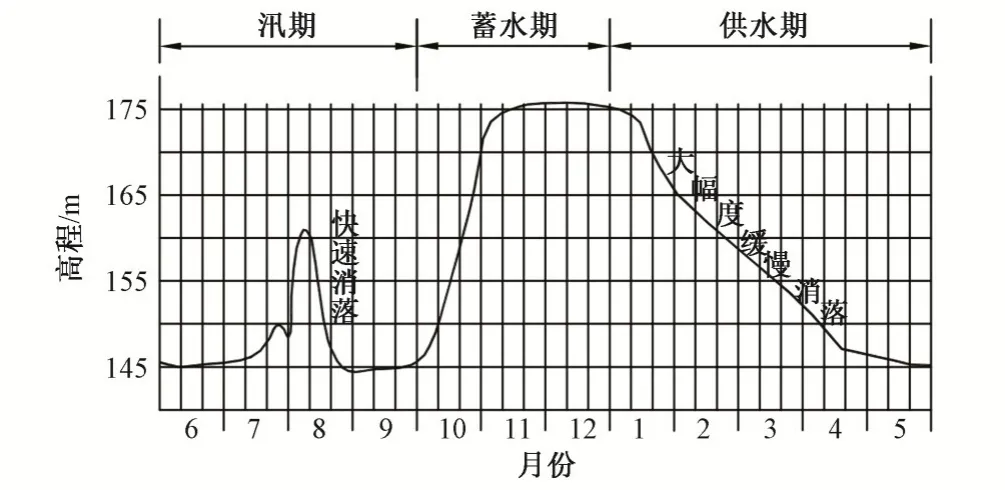
图7 三峡水库运行水位曲线图Fig.7 Chart of operating water level of Three Gorges Reservoir

由于汛期与非汛期的降雨强度并不一致，所以依据降雨资料，总结不同时期的20 年一遇与50 年一遇的区域降雨强度，如表2 所示。结合水位调动情况，在二维计算时设置7 种工况对滑坡的稳定性进行分析，具体工况如表3所示，在三维分析时设置5种工况，具体工况分析如表4所示。

表2 鸡脑壳包滑坡所在区域降雨强度 mm/dTab.2 Rainfall intensity in the area where Jinaokebao landslide is located

表3 二维计算工况Tab.3 2D calculation conditions

表4 三维计算工况Tab.4 3D calculation conditions

2 滑坡二维稳定性分析

2.1 滑坡稳定性计算结果

二维计算采用Morgenstern-Prince 法计算鸡脑壳包滑坡的稳定性，其中静水时的稳定系数为1.091。按照“三峡库区地质灾害防治工程地质勘查技术要求”，当稳定性系数f≥1.10 为“稳定”，介于1.05≤f＜1.10之间为“基本稳定”，介于1.00≤f＜1.05之间为“欠稳定”，当稳定性系数f＜1.00 时为“不稳定”，所以库水位静止时滑坡基本稳定。在库水降落与不同强度降雨耦合情况下的滑坡稳定系数变化曲线如图8所示。

2.2 二维稳定性分析

由图8 可知在仅有库水位变化的情况下，不论快速下降还是缓慢下降，滑坡的稳定性都会降低，但在高落差情况（175 m降至145 m）的稳定性明显要低于低落差情况（162 m 降至145 m），即在仅有水位调度时，供水期滑坡会更加危险。

在叠加不同强度降雨时，滑坡稳定性会出现明显的降低，由图8（a）可知，在50年一遇降雨强度下的稳定系数直接由无降雨的1.091 降至1.086，说明强降雨在滑坡体前期就作用明显，结合图8（b）可知，20年的降雨条件下滑坡前期也会明显导致滑坡的稳定性降低，但随着时间的持续，开始与无降雨条件下的稳定性开始接近，所以主要影响滑坡的稳定性的因子是水位变化和强降雨。

根据稳定系数变化曲线可知工况3（库水位从175 m水位缓降至145 m+50 年一遇暴雨）为鸡脑壳包滑坡最危险工况，此时由于库水位下降和降雨影响，滑坡的稳定系数最小值为1.032，滑坡处于欠稳定状态。

3 滑坡三维稳定性分析

采用Abaqus对鸡脑壳包滑坡在表4中确定的工况1～工况5的滑坡变形破坏过程进行模拟。

3.1 孔隙水压力计算结果分析

当水库蓄水至175 m 时，工况1 条件下孔隙水压力计算结果如图9（a）所示，此时库水位直接影响滑坡涉水区域的孔隙水压力。

图9 鸡脑壳包滑坡三维模型不同工况下孔隙水压力计算结果分布图（单位：kPa）Fig.9 Distribution diagram of pore water pressure calculation results under different working conditions of 3D model of Jinaokebao landslidte

在库水位下降且没有降雨影响时，工况2 和工况4 孔隙水压力计算结果如图9（b）、（d）所示，此时滑坡前缘地下水分布受库水位变化直接影响，当库水位下降时，滑坡前缘的地下水位相应下降，但由于滑坡前缘孔隙水压力消散需要时间，因此存在滞后性。由于滑坡后缘离库水位变化带的距离相对较远，所以滑坡后缘的孔隙水压力基本未发生变化。

在库水位下降且遭遇50 年一遇降雨影响时，工况3 与工况5 孔隙水压力计算结果如图9（c）、（e）所示，此时库水位变化和降雨联合作用直接影响滑坡前缘地下水分布，当库水位下降时，地下水位也有滞后性下降。由于滑坡后缘离库水位变化带的距离相对较远，所以滑坡后缘的孔隙水压力主要受降雨影响，而滑坡后缘的孔隙水压力受降雨影响时的变化对于滑坡整体而言并不大。

由图9 可知，涉水库岸的孔隙水压力受库水位下降的影响较大，降雨主要影响滑坡表层。

3.2 应力计算结果分析

水库蓄水至175 m水位后，大部分区域拉、压应力分布变化较小。工况1 应力分布云图如图10 所示，此时拉应力主要分布在滑体下部；滑体上部压应力值较大，中部压应力值较小。

在库水位下降且没有降雨影响时，结合应力最值统计表（表5）可知，工况2 和工况4 拉应力值减小，压应力值的绝对值增大，当库水位由175 m 缓降至145 m 时，拉应力最大值由938.3 kPa 减小为551.9 kPa，压应力最大值的绝对值由1 459 kPa 增大为1 515 kPa。拉应力主要分布在滑体下部，滑体上部压应力值较大，滑体中部压应力值较小。当库水位由162 m 水位骤降到145 m 时，拉应力主要分布在滑体下部，最大值为558.8 kPa；滑体上部压应力值较大，其绝对值的最大值为1 516 kPa；滑体中部压应力值较小。由于库水位下降使渗流场发生改变，通过渗流场与应力场的耦合作用，导致应力场的改变，这是应力场发生改变的重要原因。

在库水位下降且遭遇50年一遇降雨影响时，结合应力最值统计表（表5）可知，工况3 和工况5 拉应力值有所增大，压应力值的绝对值有所减小，当库水位由175 m 缓降到145 m 且遭遇50 年一遇降雨影响时，拉应力最大值由551.9 kPa 增大到603.9 kPa，压应力最大值的绝对值由1 515 kPa 减小到1 510 kPa。拉应力主要分布在滑体下部，滑体上部压应力值较大，滑体中部压应力值较小。当库水位由162 m 突降到145 m 且遭遇50年一遇降雨影响时，拉应力最大值由558.8 kPa 增大到635.2 kPa，压应力最大值的绝对值由1 516 kPa 减小到1 421 kPa，拉应力主要分布在滑体下部，滑体上部压应力值较大，滑体中部压应力值较小。在渗流场与应力场相互耦合作用下，库水下降和降雨的共同作用引起渗流场的改变，是应力场发生变化的主要原因。

结合孔隙水压力变化可知，水位变化与降雨作用导致渗流场变化，而渗流场与应力场相互影响，因此不同工况下应力场的改变主要是渗流场的变化。

3.3 位移计算结果分析

图11 为工况1 条件下位移分布图，此时滑体上部发生较大水平位移，滑体中下部水平位移相对较小。这是由于该滑坡为推移式滑坡，而推移式滑坡是从滑坡后缘发生变形而产生破坏。在滑体中部发生较大的向下垂直位移，滑体上部和下部向下垂直位移相对较小。这是由于滑体中部较为陡峭，使其在自重作用下产生较大的向下垂直位移，而上部和下部相对较为平缓，垂直位移相对较小。

汇总滑坡位移最大值得到表6，对比工况2～5 的水平位移，4 种工况下较大水平位移均发生在滑体上部，在库水位下降且没有降雨影响时，工况2和工况4的水平位移均大于工况1时的水平位移，这是由于库水下降，滑体内产生向外的渗透力，使滑体下滑力增大，导致滑体水平位移增大，但水位下降速率对水平位移影响不大。在库水位下降且遭遇50年一遇降雨影响时，由于滑坡的渗透力进一步增大，滑动力也随之增大，导致工况3和工况5 的水平位移大于工况2 和工况4，其中工况3 条件下滑坡的水平位移最大。

表6 滑坡位移最大值统计表Tab.6 Landslide displacement maximum statistical table

对比工况2～工况5 垂直位移，滑坡中部均发生较大的向下垂直位移，而滑坡上部和下部向下垂直位移相对较小。在库水位下降且遭遇50 年一遇降雨影响时，垂直位移最为明显，其中工况3 时垂直位移最大，这是由于库水位下降导致滑体向下滑移，同时在自重和降雨作用下，使滑体产生的向下垂直位移增大。当库水位下降且没有降雨影响时，对比工况2 和工况4 的垂直位移场分布，此时工况2 滑体中部的垂直位移量为4.35～26.55 mm，滑体上部垂直位移相对较小，量值为0～19.81 mm，滑体下部垂直位移较小，量值为0～13.08 mm；而工况4 滑体中部的垂直位移量值为6.55～26.44 mm，滑体上部垂直位移相对较小，量值为0～19.73 mm，滑体下部垂直位移较小，量值为0～13.02 mm。结果表明水位下降速率对滑坡的垂直位移有影响。

4 数值预测模拟

由数值计算分析结果可知工况3（库水位由175 m水位缓降到145 m 水位+50 年一遇降雨）为鸡脑壳包滑坡最不利工况。提取滑坡主滑剖面上地表位移监测点WS07-04、WS07-05 和WS07-06，如图12 所示。在最不利工况（工况3）下各监测点的位移变化如图13所示。

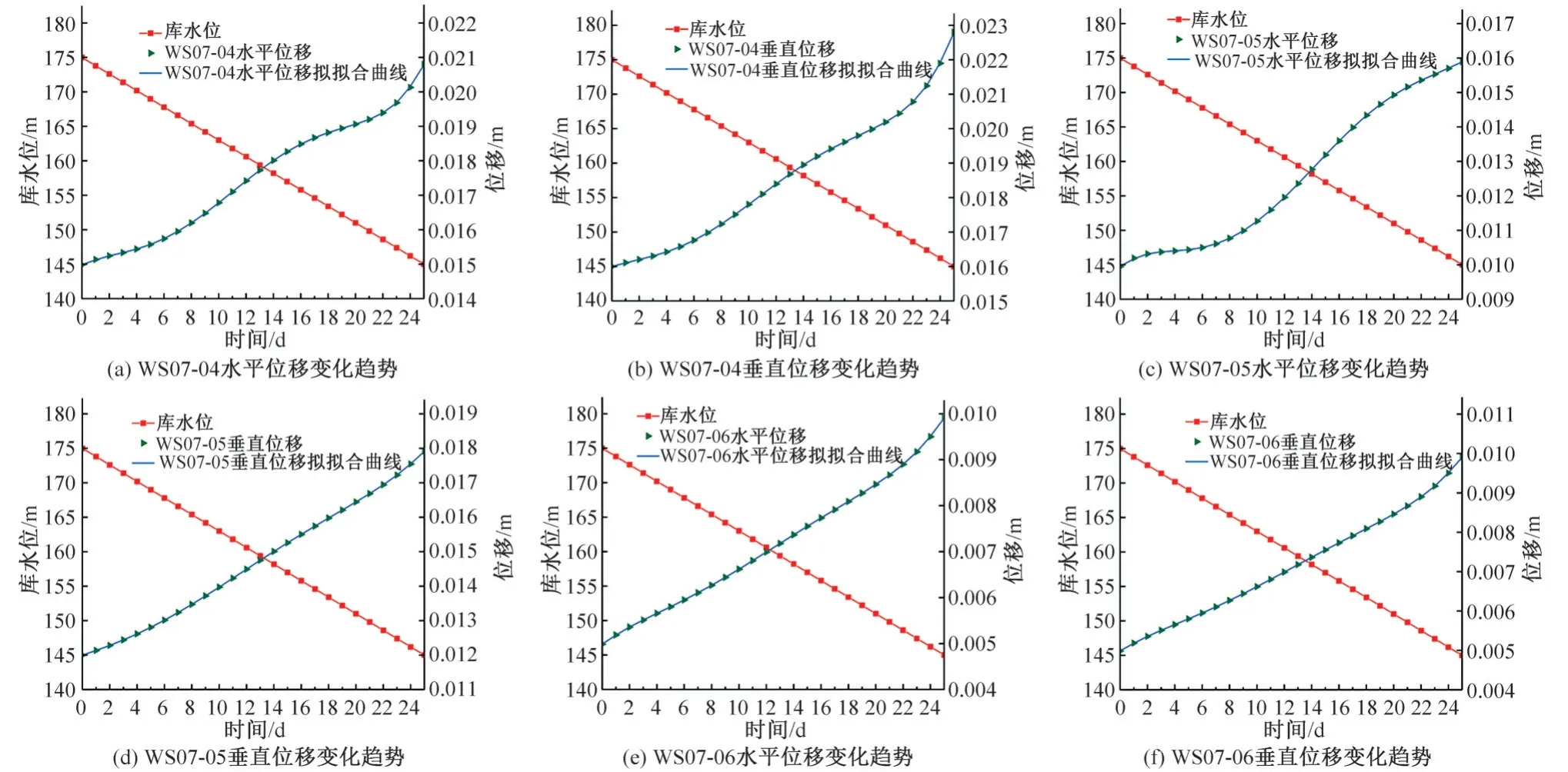
图13 监测点WS07-04、WS07-05、WS07-06位移变化趋势Fig.13 Change trend of displacement in monitoring points WS07-04， WS07-05 and WS07-06

根据监测点位移变化趋势可知工况3（库水位由175 m水位缓降到145 m 水位+50 年一遇降雨）条件下，处于滑坡中后部的地表变形监测点WS07-04 和WS07-05 的位移远大于滑坡前部的地表变形监测点WS07-06位移，说明滑坡的位移主要发生在中后部。

5 库水位下降速率、降雨与滑坡稳定性关系

5.1 库水位下降速率与滑坡稳定性关系

为进一步分析库水位下降速率与滑坡稳定性关系，取不同库水位下降速率进行滑坡渗流计算，由于二维计算结果表明工况3（库水位从175 m 水位缓降至145 m+50年一遇暴雨）时滑坡最危险，所以基于此条件下仅改变库水位下降速率作为变量对滑坡进行分析，计算时以1.2m/d 为初始下降速率逐渐增加，每增加0.2 m/d 为一档，采用Morgenstern-Prince 法计算滑坡在不同库水降速下的稳定系数，计算结果见表7。

表7 不同库水降速下滑坡稳定系数Tab.7 Stability coefficient of downhill slope of different reservoir water slowdowns

由表7可知，随着库水下降速率的增大，滑坡的稳定系数逐渐减小，库水下降速率从1.2 m/d 增加到4.2 m/d 时，稳定系数从1.032降至0.997，处于失稳状态。

从图14 可知，随着库水下降速率的增大，滑坡的稳定性逐渐降低，主要是由于库水位下降对滑坡产生渗流作用，渗流场受降速的影响很大，库水位下降速率越大，渗透力也越大，滑坡稳定性系数越低。所以应加强滑坡地表位移的监测，做好灾前预报和准备工作，及时防治可以有效减少及避免滑坡的发生。

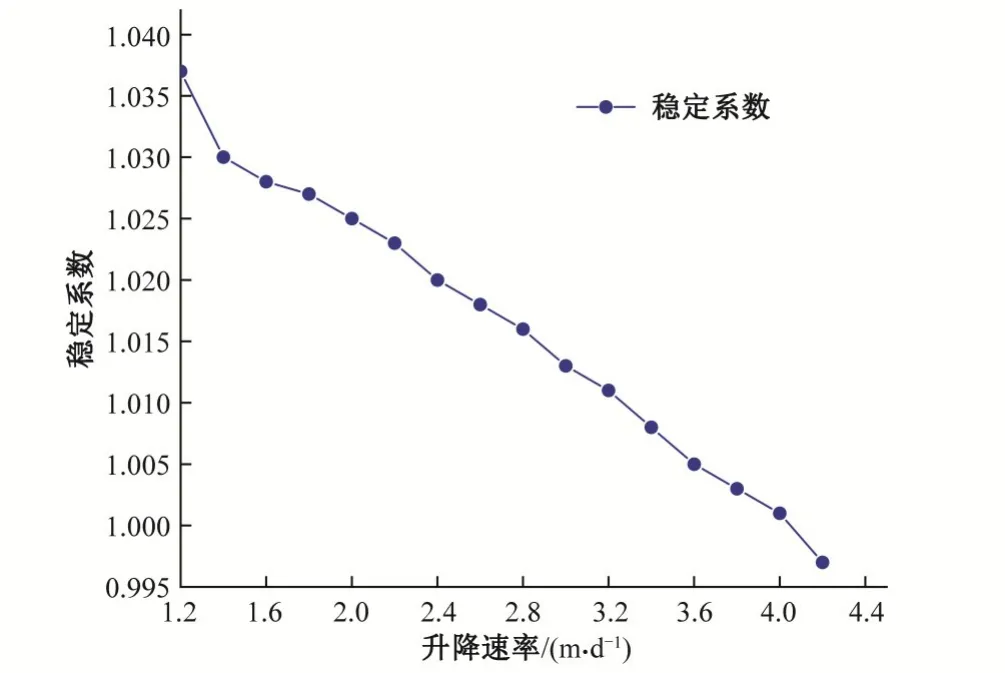
图14 不同库水降速下滑坡稳定系数Fig.14 Stability coefficient of downhill slope of different reservoir water slowdowns

5.2 降雨与滑坡稳定性关系

为了分析降雨与滑坡稳定性关系，取100 年一遇暴雨和50年一遇暴雨对应的降雨强度和3 天、4 天、5 天的降雨历时进行组合。采用Morgenstern-Prince 法，计算滑坡在不同降雨条件下的稳定系数，计算结果见表8。

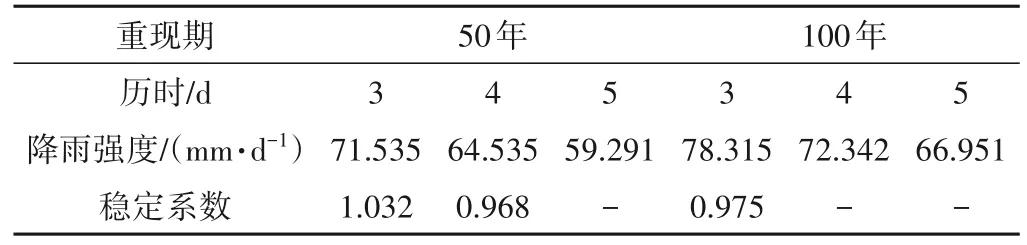
表8 不同降雨条件下滑坡稳定系数Tab.8 Landslide stability coefficient under different rainfall conditions

由表8可知，随着降雨时间和降雨强度的不断增加，滑坡的稳定系数不断减小；当降雨过程为重现期100 年、历时3 天（降雨强度为78.315 mm/d）时，滑坡稳定系数为0.975，处于失稳状态；当降雨过程为重现期50 年、历时4 天（降雨强度为64.535 mm/d）时，滑坡稳定性系数降至0.968，处于失稳状态。

6 结 论

（1）根据二维稳定性分析可知，主要影响滑坡的稳定性的因子是水位变化和强降雨，其中库水位从175 m 缓降至145 m且遭遇50 年一遇暴雨时，为鸡脑壳包滑坡最危险工况，此时滑坡的稳定系数最小值为1.032，滑坡处于欠稳定状态。

（2）根据三维变形破坏分析可知，库水位下降与强降雨造成滑体内渗流场发生很大变化，使坡体内的渗透力发生很大的改变，进而引起位移发生很大的变化；鸡脑壳包滑坡在库水位由175 m 水位缓降至145 m 水位并且叠加50年一遇降雨条件下位移最大。因此，工况3为鸡脑壳包滑坡最不利工况，此时滑坡位移主要发生在滑坡中后部。

（3）库水位下降速率与滑坡稳定性关系的分析表明，滑坡的稳定系数随着库水降速的增大而减小，当库水下降速率为4.2 m/d 时，滑坡的稳定性系数为0.997，此时滑坡处于失稳状态。降雨与滑坡稳定性关系的分析表明，滑坡的稳定系数随着降雨强度和降雨时长的增大而减小。因此，库水位下降速率越大、降雨强度越大、降雨时长越长，滑坡越容易失稳。

（4）综合以上分析，库水位下降和降雨对鸡脑壳包滑坡的稳定性影响较大。鉴于滑坡岩土体物理力学参数在经历多次水库水位波动和降雨过程会发生变化的现实，建议加强观测，并根据观测结果及时反演更新滑坡物理力学参数。以此为基础，对滑坡在后续蓄水和降雨条件下的变形破坏过程进行及时预测分析，为该滑坡的监测预警提供合理可靠的依据。