阀门类型对离心泵输水系统停泵特性影响研究

2023-09-22刘跃飞

中国农村水利水电 2023年9期

张醒，刘跃飞，姜劲

（1. 施耐德电气（中国）有限公司，江苏南京 210019； 2. 金陵科技学院机电工程学院，江苏南京 211169）

0 引言

停泵过渡过程为泵站运行中常见的大波动过渡过程，其历时较短且常伴随着剧烈的压力波动和频繁流态转换［1］。出口阀门在停泵开始后迅速动水关闭，起到关键断流作用，同时其关闭过程中常伴随流场的剧烈变化［2］，甚至出现漩涡、空化和水击等威胁水泵和输水系统运行安全的现象，因而针对停泵过渡过程中出口阀门的研究对水泵输水系统的安全运行十分重要［3，4］。

模型试验是研究水泵输水系统特性的基础［5，6］，但一方面水泵过渡过程的模型试验难度大，成本高，部分工况具有危险性［7］；另一方面，输水系统模型试验的比尺选择主要依据水泵及管道的几何特性，很难做到模型阀门的等比例还原，若要实现阀门部件与原型相似，会大幅增加模型试验难度［8］，已有模型试验研究较少探究阀门偏差，以及阀门类型对停泵特性的影响。数值计算中的一维特征线法（MOC）以实验获得的水泵特性曲线为求解边界条件，结合一维离散管道水锤方程求解含水泵输水系统瞬态特性，其对阀门部件多为简化处理，采用通用经验模型处理阀门边界，较难体现不同阀门特性对系统瞬态过程的影响［9］。

随着计算流体力学（CFD）数值模拟方法的广泛运用，水力过渡过程问题中应用CFD 方法进行数值分析愈发成熟，三维数值模拟方法不仅能直观反映水泵内流特性，同时能体现阀门部件的流场特性［10，11］。蝶阀、球阀与闸阀是泵站出口阀门的3 种常见型式。在泵站及水电站过渡过程的数值模拟研究中，由于3 种阀门几何结构不同且阀体运动方式有所差异，在CFD 数值模拟中采用的不同模拟方法如下：通常而言，球阀的启闭模拟最简便，Moujaes S F［12］等人使用STAR-CD 软件对不同开度下的球阀进行三维CFD 模拟分析，张亚武［13］等人采用滑移网格（Moving Mesh）方法控制阀芯运动，模拟甩负荷工况下主进水阀关阀过程；蝶阀在CFD 数值模拟可以采用滑移网格的方式，Leutwyler Z［14］等人采用三维CFD 方法对蝶阀的流量、转矩、压力等参数进行三维模拟预测，周大庆［15］等人滑移网格法控制转轮与蝶阀转速的改变，完成混流泵站开机过程数值模拟；蝶阀模拟也可以采用几何重构的动网格方法，何庆中［16］等人采用几何重构的动网格方法对三偏心蝶阀开启过程出现的涡街现象进行数值模拟；闸阀可采用动网格中的铺层方法实现，夏鹤鹏［17］利用动网格的铺层方法模拟快速闸门的启闭。可见，针对不同的阀门类型的CFD 模拟方法有差异，在数值模拟中的难易程度也不尽相同，而已有研究较少针对不同类型阀门对系统停泵特性影响进行研究，且基于三维瞬态CFD 方法对系统中阀门类型差异的研究更少［18］。若能厘清不同阀门类型对水泵输水系统过渡工况影响的异同点，一方面可实现CFD 数值模拟中不同阀门类型的相互替换从而使模拟过程简化，另一方面对模型实验中阀门部件的选择，对改善模型试验中阀门部件的相似性误差具有理论指导意义。

本文构建含离心泵输水系统的三维数值模型，基于CFD 商用软件及动网格方法提出了含不同类型出口阀门的输水系统停泵过渡过程数值仿真方法。分析不同出口阀型式对停泵过渡过程的水泵特性参数变化的影响及对应参数极值间的差异，结合流场内特性揭示差异形成的原因，并探究不同关阀时间对阀门间差异的影响。

1 数值计算方法及模型

1.1 基本方程

水泵输水系统的停泵过渡过程中，工作介质为水，热量交换较小，因而可不考虑能量方程的影响［19］，其求解的连续性方程和动量守恒方程分别为：

由于停泵工况常伴随着压力的剧烈波动及压力波在输水管道内传播，水体的压缩性需要考虑。结合软件FLUENT 中用户自定义方法（UDF），在设置水体的压缩性时将流场内计算节点处的密度和波速表示为节点压强的函数，体积弹性系数及波速表示为公式如下：

将初始压强与密度值代入公式（3）得公式（5），进一步求解得节点波速与节点压强的关系为公式（6）：

式中：p为水压强；p0为环境压强，取值0；ρ为水密度；a为水锤波速；ρ0为初始水密度，为1 000 kg/m3；K为水体积弹性系数，为2.2×109Pa。将公式（6）应用于管道的水锤计算时，其与实际水锤波速有轻微偏差，但本文的关注点主要为数值模拟中不同阀门型式对停泵过渡过程的影响，在同样的参数设置下，管道水锤波速的轻微偏差可忽略。

1.2 计算模型及网格

计算模型为含离心泵输水系统，其整体三维几何模型如图1 所示，模型包含离心泵，液控出口阀，压力箱，输水管道等部件。计算模型与原型比尺为1∶1，额定流量为13 m3/s，水泵的额定扬程为48.0 m，水泵额定转速为300 r/min，转动惯量为2 500 kg·m2，电机功率为9 000 kW，叶轮直径为2.8 m，叶片数为6，叶轮中心高程为-16.3 m，阀门直径为2.6 m，水泵前后输水管道总长度为200 m左右。数值计算中出口阀有蝶阀，球阀，闸阀三种型式，配置不同类型阀门时仅阀门部件模型发生替换，其他部件如水泵、管道的几何模型均相同。额定运行状态下，水由恒定水位的上游水库流入上游进口，经管道、水泵、出口阀门、压力箱等部件后经下游出口进入恒定水位的高位水池。

图1 离心泵输水系统三维几何模型Fig.1 3D model of water delivery system with centrifugal pump

采用结构化网格划分管道、压力箱、球阀和闸阀部件，对于空间扭曲较大的离心泵和蝶阀部件采用非结构化网格划分，图1 中展示了三种阀门的局部网格结构。通常而言，更多的网格数量对应更精确的计算结果，但增加网格数量会相应地增加数值计算的时间成本，因而在计算精度与计算速度之间寻找平衡十分必要［20］。选取网格总数为158.4 万、259.5 万和335.8 万的方案1、2、3 三种网格划分方案，3 种网格划分方案对数值模拟结果局部略有影响，但不改变总体趋势。在停机瞬态工况下，方案2 与3 的最大反向转速极值相差小于1.3%，综合考量计算精度与时间成本，选择方案2为最终的网格划分方式，其网格总数为259.5万。

1.3 数值解法及边界条件

计算采用三维CFD 商用软件FLUENT 16.0，数值计算模型为：对流项为二阶迎风格式；扩散项为中心差分格式；速度压力的耦合方式为压力的隐式算子分割算法（PISO）；湍流模型为Realizablek-ε湍流模型［21，22］。模型边界条件主要为上下游进出口、叶轮转动和阀门关闭过程，管道进口和出口采用压力进出口边界条件［23］，进出口剖面网格节点上的压力值呈梯形分布，由各个节点几何高程与水面距离换算得到，并由UDF 输入关于节点高程的函数表达式后赋值，上游水面高程-1.3 m，下游水面高程43.7 m。叶轮转动基于滑移网格（Moving Mesh）方法［24，25］，其控制规律通过UDF 功能控制，具体为：水泵正常运行工况下，设置叶轮的转速n恒定为300 r/min，在2 s开始停泵后，叶轮转速由公式（7）控制，并在每个时间步进行更新。

式中：M为停泵叶轮叶片力矩；J为转动部件转动惯量；dt为时间步长；dω为角速度差，ωn表示当前步角速度；ωn+1表示下一步角速度。为了简化模型，公式（7）中省略了叶轮转动机械摩擦力矩和发电机转子阻力矩。

出口阀门采用直线关闭规律，额定停泵工况下阀门开度随时间的变化规律如图2 所示，离心泵叶轮于2 s 断电，出口阀门同时开始关闭，经20 s 后于22 s 时完全关闭。3 种不同类型阀门的关闭过程如图3 所示，其中蝶阀与球阀模型采用滑移网格方法控制阀体的转动，闸阀模型采用铺层网格方法控制阀体关闭。

图2 额定工况停泵时阀门与叶轮控制规律Fig.2 Control law of valve and impeller under rated stopping condition

图3 3种不同类型阀门的关闭过程Fig.3 Closing process of different types of valves

2 结果与分析

2.1 不同阀门类型对水泵外特性的影响

图4为额定关阀时间下出口阀门类型不同时停泵过程中各参数变化图，主要为流量Q、转速n、扬程H与轴向水推力Fz的变化规律，其中叶片轴向力的正方向为向下。当出口阀为蝶阀时的停泵过渡过程如下：在离心泵断电同时，出口阀门开始关闭，机组流量于4.38 s 时降为0，转速于5.23 s 时降为0，因而停泵过程的3 个工况阶段为：2～4.38 s 为停泵水泵工况，4.38～5.23 s 为停泵制动工况，5.23 s 之后为停泵水轮机工况，且各参数于22 s后逐渐趋于稳定值；在停泵水泵工况期间：水泵流量、转速迅速下降，水泵扬程H先迅速下降，之后在0 值附近小幅振荡；叶轮的轴向力水推力Fz于2.59 s 时达到反向最大值-20.83 kN；在停泵制动工况期间：机组流量倒流，叶轮转速方向为正且转速值减小；在5.23 s之后的停泵水轮机工况期间：水泵机组流量和转速均为反向，且水泵流量与转速的反向最大值均出现在停泵水轮机工况，反向流量于10.49 s 时达到反向最大值-12.9 m3/s，反向转速于10.64 s时达到反向极值-327.56 r/min。

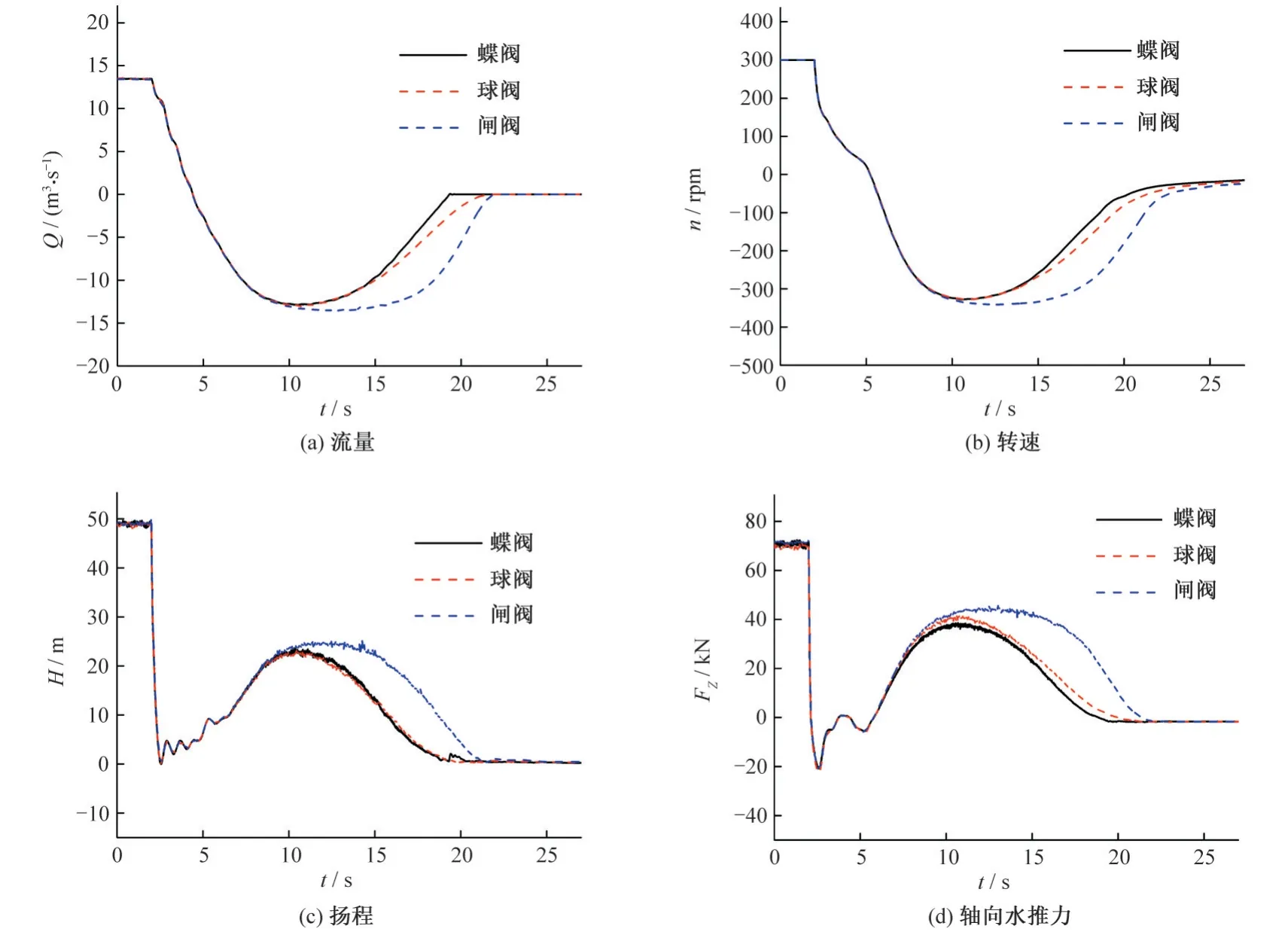
图4 设置不同类型阀门停泵过程的参数变化Fig.4 The changing laws of parameters with different valves

水泵出口阀为球阀时，停泵过程中的参数变化曲线与蝶阀时的差异较小。此时水泵流量在4.40 s 时降为0，转速在5.24 s时降为0，流量和转速的变化在15 s 之前与出口阀为蝶阀时的曲线近乎重合。在15～22 s，配置球阀时的流量减小速率相较蝶阀略缓慢，原因是蝶阀阀体在关阀后期对流量有更强的截断效应。

水泵出口阀为闸阀时，其停泵过程的前半段与前二者差别较小，而其后半段有较大差异。在停泵前半段水泵流量于4.37 s 时降为0，转速于5.21 s 时降为0，数值与其他阀门类型近似。水泵流量、转速、扬程与叶片轴向力变化曲线的差别主要集中在关阀的后半部分，在10～22 s 时间段内，流量及转速的反向极值略大于出口阀为蝶阀和球阀的工况，而其反向流量与转速的减小速率远小于配置蝶阀与球阀时的情况，可见当出口阀门为闸阀时，在同样的关阀控制规律下，闸阀的截流能力在三者中最小，且远小于其余二者。

表1 为出口阀门为蝶阀、球阀和闸阀的水泵停泵过程中反向流量、反向转速及反向轴向力的最大值，其中配置蝶阀与球阀时的反向极值数值相近，而配置闸阀时的反向极值差别明显。由于轴向水推力在反向极值时刻处于小幅正当状态，因而3种阀门下的轴向水推力的反向极值有小幅区别。配置闸阀对参数反向极值的影响主要体现在流量和转速上，配置闸阀时的反向流量及反向转速均增加，且由图4 可知配置闸阀时发生反向流量与转速极值的时间点均大幅延后于配置蝶阀与球阀时的工况。

表1 停泵过程中各参数的反向极值Tab.1 Reverse extreme values of parameters

综上可知，配置3 种不同类型出口阀门水泵按相同直线关闭规律停泵后，配置闸阀的水泵停泵特性与其他二者差异明显，其中参数的反向极值差异主要体现在流量和转速上，相较于蝶阀，配置闸阀时最大反向流量增加5.2%，最大反向转速增加4.1%。

2.2 不同阀门类型对流场内特性的影响

停泵过程中，伴随着流量与叶轮转速的迅速变化，输水系统内流场变化频繁，其中更以叶轮及阀门区域为最，不同阀门类型对流场变化的影响可与外特性参数的变化规律相互印证。初始0 s时的叶轮旋转方向为顺时针，图5为停泵过程中配置不同出口阀门时叶轮叶片压力分布对比图，压力分布所在时间点均为13 s，叶片外侧为压力面，内侧为吸力面。在13 s 时，各工况水泵均处于停泵水轮机工况，水流反向且反向流量较大，叶轮旋转方向转换至逆时针，原先叶片出口变为水流进口，水流进入叶轮区域产生的撞击与脱流造成了13 s 时叶片上的局部高压与负压区域，易出现负压空化的不利现象。当出口阀门类型不同时，其压力分布的差异与内特性参数之间的差异规律相似，即配置蝶阀与球阀工时叶片压力分布差异较小，而配置闸阀与前二者的差别增加，主要体现为叶片压力面上的低压区范围更小，其吸力面上的高压区范围更大，而这与图4中配置闸阀的扬程在13 s时更大的结果相一致。

图5 停泵过程中叶轮叶片上的压力分布Fig.5 Pressure distribution on blades during shutdown

由图4 与图5 已知在停泵过程中，水泵外特征参数变化曲线及叶片压力分布在配置蝶阀与球阀时差异较小，因而在分析配置不同阀门类型的停泵过程阀门区域流场差异时，仅选取蝶阀与闸阀为对比对象，省略球阀。图6 为额定停泵工况下阀门区域的压力与速度变化对比图，由图2 阀门关闭控制规律可知不同类型阀门关闭时间均为2 s至22 s，图中的方向标识为额定运行状态下的水流流向。在停泵过程中，阀门左侧水泵侧的压力呈现逐渐减小趋势，阀门右侧压力箱侧的压力呈现先减小后增大趋势。比较配置蝶阀与闸阀时的压力及速度分布变化可见两者有较大的不同：在阀门关闭过程中，蝶阀水泵侧的压力变化减小速度较闸阀更快，且蝶阀压力箱侧的压力上升速度也更快。比较不同阀门类型对管道内流速的影响可见，在11 s时，蝶阀的上下侧均出现因流道急速收缩而出现的高速区域，而闸阀管道内的高速区域在13 s 时才出现，即在相同的直线关闭规律下，由阀门处的内特性流场变化可知，蝶阀对水流的截断效应更强，这与图4 中参数特性变化所反映出来的规律相一致。

图6 蝶阀与球阀部件处的流场变化Fig.6 Variation of flow field for butterfly valve and ball valve

2.3 缩短关阀时间对配置不同阀门时差异的影响

额定工况下的阀门控制方式为2 s 至22 s 历时20 s 的直线关闭规律，为探究不同关阀时间下配置不同阀门时的差异，缩短直线关阀时间至5 s，此时停泵参数的变化曲线如图7 所示。与额定20 s 停泵工况相似，当关阀时间为5 s 时，水泵内依旧有倒流现象，转速同样发生反转，但是反向流量及反向转速的极值大幅减小。对比扬程变化曲线可见，在20 s 关阀工况时，扬程曲线后段为平缓降至0，而在5 s 关阀工况时，扬程曲线后段伴有强烈振荡。这是由于在两种工况的关阀后段，流量均为倒流，20 s工况的关阀时间更长，流量减小时间较5 s工况更长，在5 s 的关阀工况中，倒流流量在极短时间内降为0，导致水泵出口处压力的迅速减小及之后的压力振荡，同时体现为扬程曲线上的减小及振荡。

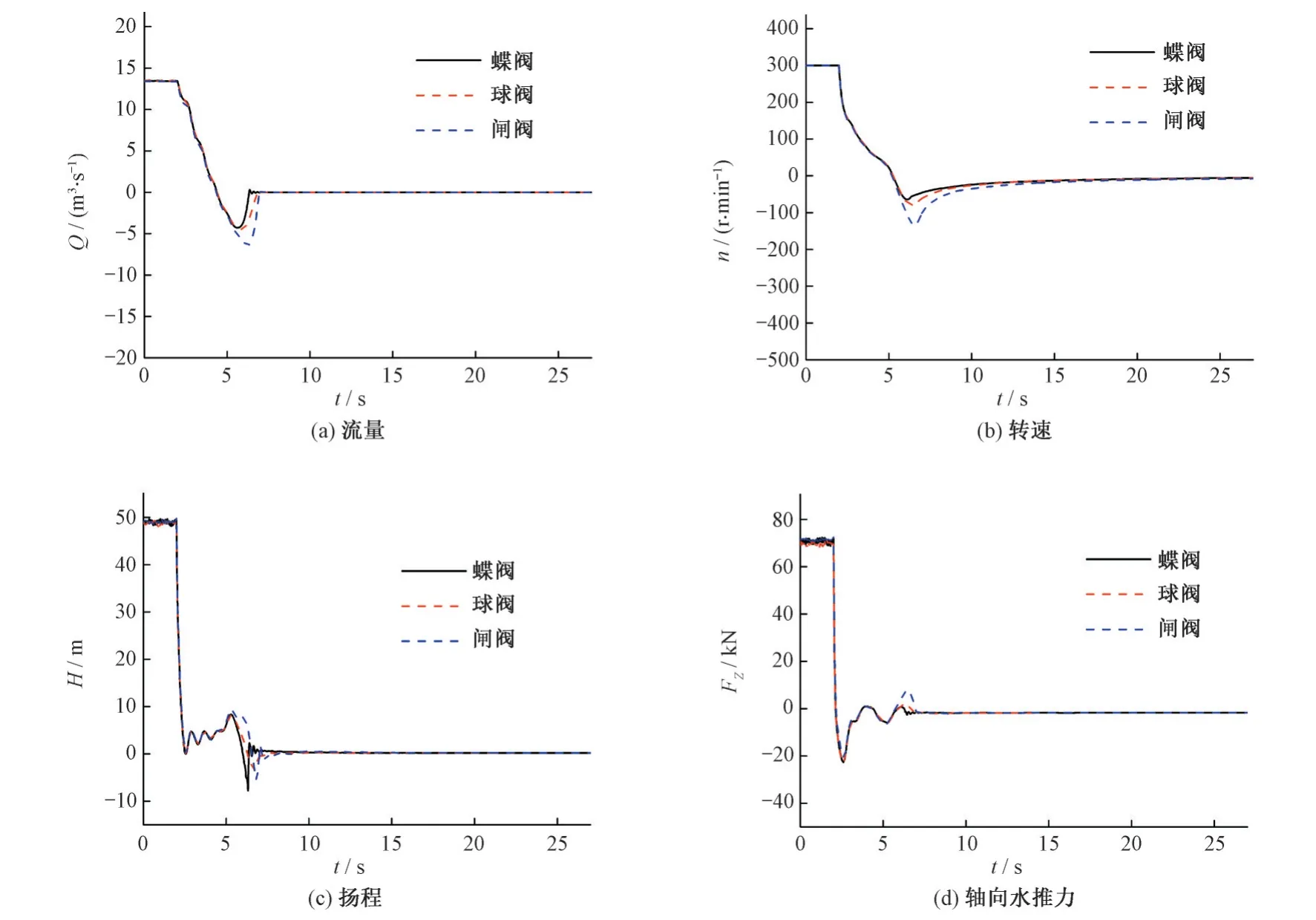
图7 关阀时间为5 s时的停泵参数变化Fig.7 Changes of parameters when valve′s closing time is 5 s

在5 s 之前，配置不同阀门的停泵参数变化曲线是相似的，轴向水推力的反向极值发生在停泵刚开始时刻，因而配置不同阀门类型的轴向水推力反向极值在5 s 关阀时同样差别不大。配置不同类型阀门的停泵扬程曲线变化整体是相似的，均为关阀开始时的迅速下降，及关阀末期的小幅振荡。比较流量与转速变化曲线，可见配置蝶阀与球阀时的停泵参数曲线较闸阀更加接近，配置闸阀的停泵参数曲线较前二者有较大差别，且其流量与转速在倒流时段内的差别较20 s 关阀工况的差别显著增加。

表2 为关阀时间为5 s 时，出口阀门为蝶阀、球阀和闸阀的停泵过程中反向流量、反向转速及反向轴向力的最大值，而配置闸阀时的反向极值百分比差别显著大于时间为20 s 的情形。配置闸阀的5 s 关阀工况下时，其流量的反向极值超出配置蝶阀工况的50%，其转速的反向极值超出配置蝶阀工况的100%，而这两个数值在关阀时刻为20 s时均小于10%。产生这一差异的原因是在20 s关阀时反向极值出现在关阀中间时段，而在5 s关阀时反向极值出现在关阀的末端，由章节2.1 及2.2 的分析已知闸阀与其余二阀门的差异主要集中于关阀后段，因而在5 s关阀工况中，配置闸阀停泵参数的反向极值与其余二阀门的差异增大。