长距离调水工程渠道裂隙岩质边坡渗流模拟

2023-09-22黄兆虎方攀博韩延成邓晓川宋广增赵嘉诚

中国农村水利水电 2023年9期

黄兆虎，方攀博，韩延成，王栋，邓晓川，宋广增，赵嘉诚

（1. 济南大学，山东济南 250022； 2. 山东省水利勘测设计院有限公司，山东济南 250013；3. 山东省调水工程运行维护中心潍坊分中心，山东潍坊 261000）

0 引言

明渠输水工程是实现我国水资源调度，保证水资源平衡的重要举措，例如南水北调中、东线，引黄济青工程、胶东调水工程等均采用明渠形式。然而，由于长距离调水工程距离长，经常会经过裂隙发育地区。裂隙发育地区的岩质边坡，其渗流特性和与土质边坡渠道不同［1］。裂隙的复杂分布以及地下水在裂隙岩体中的分布和渗流的不均匀性致使裂隙岩体渗流问题研究极其复杂。由于裂隙渗流的复杂性，以往长距离调水工程渠道渗流都是按孔隙模型进行渗流计算的，忽略了裂隙对渗流场的影响，而实际运行中渗透破坏时常发生，进而影响供水安全甚至发生严重的输水事故。

渗流对大坝、渠道等水工建筑物边坡稳定性、渗透破坏具有重要影响［2］，国内学者在渠道边坡渗流方面进行了广泛的研究。高丹盈等［3］用有限元方法进行了南水北调工程大沙河段渠道排水非稳定渗流计算分析；朱国胜等［4］对逆止式排水系统对南水北调中线渠道边坡渗流控制效果进行了研究；钟登华等［5］构建了南水北调中线工程某渠段的工程地质信息三维可视化模型，运用耦合方程，对研究区域进行渗流模拟，并采用流固耦合进行渠道稳定性计算，结果表明渠道渗流对其稳定性影响较大；左海凤、王光谦等［6］建立了南水北调中线磁县段三维水文地质结构模型，进行了地下水排水数值模拟；方攀博等［7］研究了渠道排水管的不同布设位置对渠道渗流及扬压力的影响；陈思涵等［8］研究了高地下水位地区管、井相结合的复合排水方案及渗流场的模拟、减压效果研究。

国内外学者在裂隙渗流方面也进行了广泛的研究，在裂隙岩体渠道边坡渗流方面，上世纪四五十年代前苏联的一些学者Волоэько 和Ломизе 等就对裂隙介质（岩体）的水力学问题进行了试验研究，并最早提出了单裂隙岩体地下水运动的立方定律［9］。但在1963年法国Malpasset拱坝失事事故发生后，岩体裂隙渗流开始了更充分的研究。1965 年Snow［10］创立了岩体裂隙渗透率张量理论。李定方、万力［11］采用有限元法分析渗流对岩体高边坡的影响。张家发、李思慎、叶自桐［12］采用有限元分析法模拟分析了多年平均降雨条件下高边坡岩体的稳定渗流状态。在岩体饱和-非饱和流的渗透规律方面，Brooks-Corey 在1964 年提出了适用多孔介质的渗透特性的Brooks-Corey 模型。Mualem 于1976 年首次提出了适用于多孔介质的Mualem 模型，并验证了此模型的适用性［13］。Van Genuchten［14］于1980 采用物理实验法拟合孔隙介质模型得出非饱和裂隙渗流的重要模型Van Genuchten（VG）模型。黄涛等［15］将VG 模型和Mualem 模型结合在一起提出适用于两相多孔介质的VG-Mualem 模型，经计算VG-M 模型与试验结果的拟合效果最佳。平扬等［16］基于压水试验分析了不同自重应力以及岩性等因素对裂隙岩体渗透性的影响；鲁志强等［17］进行了裂隙水作用下水利岩质边坡抗倾覆动力稳定性研究，胡小昕等［18］进行了基于裂隙网络有限元的地下洞室围岩位移反演分析。

综上所述，学者们分别对渠道边坡渗流、裂隙渗流进行了广泛的研究，目前在渠道设计时，渗流分析通常采用孔隙模型，在裂隙对渠道边坡渗流的影响及孔隙模型与裂隙模型对渠道渗流影响对比方面缺乏研究。

山东省胶东调水工程是南水北调东线工程中山东“T”字型调水大动脉的重要组成部分，是缓解胶东地区水资源供需矛盾的重要水利基础设施。但该工程莱州段部分渠段裂隙较多，所以通水以来每次停水检查时均会出现大量的渗透破坏（见图1），严重影响工程安全和供水安全。换言而知，在远小于设计地下水位的情况下，仍然产生了大量的渗透破坏。破坏位置呈现点状分布，开展渠道裂隙渗流的研究具有十分重要的现实意义。

图1 渠道衬砌渗透破坏情况Fig.1 Seepage damage of channel lining

1 研究区概况及水文地质勘探

研究区位于胶东引黄调水工程莱州段，莱州市境西南部沿海低缓丘陵区，地处趴埠周家桥（桩号62+509）至后趴埠东交通桥段（桩号64+909）之间。东经119°49′33.213″～119°51′20.358″，北纬37°10′10.380″～37°11′19.691″。研究区西北为渤海，直线距离2.0 km。距离莱州市城区9 km，属于温暖带季风区大陆性气候，四季分明气候温和湿润（图2），多年平均气温12.4 ℃。1990-2019 年多年平均降水量为638.80 mm，最大年降水量为907.0 mm（2001 年）。研究区内地表水体不丰富，在研究区西侧有朱流河经过，为季节性河流，常年水量短缺。研究区地层岩性简单，主要为古元古界粉子山群岗箭组二云片岩、黑云片岩夹黑云变粒岩，巨屯组含石墨黑云斜长变粒岩及石墨大理岩等（图3）。

图2 莱州市1990-2019年降水量图Fig.2 Precipitation map of Laizhou City from 1990 to 2019

图3 研究区地质图Fig.3 Geological map of study area

根据项目研究需要，在研究区布设了三眼勘测井（渠左南SK1 井、渠右南SK2 井、渠右北SK3 井），得到了岩芯，进行了渗水试验［19］，安装3 套水位自动观测设备和1 套渠道水位观测设备。在济南大学进行了相关渗水实验，渗水实验所得渗透系数如表2所示。

2 模型计算原理

2.1 裂隙生成原理

目前直接获取整体岩体边坡的裂隙几何分布是十分困难的，研究者通常采用钻探得到的岩芯，采用统计方法来获取裂隙几何信息［20］。但这种方法所研究的范围较小，覆盖面不足，不能很好体现岩体内大范围的裂隙几何特征。本文通过钻探获取岩芯（图4）统计裂隙几何基本信息，基于蒙特卡罗法，利用MATLAB 语言编制二维离散化裂隙网络程序生成渠道边坡裂隙分布。

图4 研究区域明渠两岸钻孔岩心Fig.4 Borehole cores on both sides of open channels in the study area

2.1.1 随机裂隙网络基本假定

对于要生成的裂隙网络，进行如下5条假定［23］。

（1）裂隙网络中裂隙的主要几何参数有：迹长L、裂隙宽度、裂隙的分布密度和裂隙的倾角θ（即迹线与X轴方向的夹角）。

（2）对于生成裂隙，主要由裂隙的中心点（X0，Y0）、裂隙的迹长L、倾角θ、裂隙的两端端点确定。裂隙两端点的坐标表达式为：

端点1（X1，Y1）：

端点2（X2，Y2）：

（3）生成裂隙结构面的迹线为直线段，结构面的长度为裂隙的迹长、宽度为裂隙的张开度，结构面的产状由裂隙的倾角确定。

（4）裂隙的数量由生成域的面积乘该组的裂隙密度得到。

（5）若有裂隙不位于和不完全位于研究边界，位于研究域外的裂隙部分进行删除。

2.1.2 裂隙网络几何参数确定

裂隙的生成需要对裂隙的各参数进行确定。具研究表明［21，22］，一般情况裂隙中心点服从均匀分布，裂隙迹长服从负指数分布或对数正态分布，裂隙倾角服从正态分布或对数正态分布，裂隙的密度服从负指数分布，裂隙的张开度服从负指数分布或对数正态分布。本文通过钻孔调查、根据裂隙各参数分布规律进行计算分析，将研究区的裂隙组分为两组，得到各组裂隙的初始几何参数如下表1所示。

表1 裂隙初始几何参数Tab.1 Initial geometrical parameters of fracture

2.2 饱和-非饱和渗流微分方程

由于渠道两侧降雨入渗对渠道边坡渗流有影响。因此本文采用饱和-非饱和渗流微分方程进行渗流计算。

Darcy 定律是用来描述多孔介质中流体流动的方程，以孔隙水压力为自变量，其微分形式如下［24］：

式中：K(θ)为土壤含水率函数；Hm为土水势。

饱和渗流微分方程为：

式中：ε为孔隙率；ks为饱和渗透系数；p为孔隙水压力；ρ为流体密度；g为重力加速度；D为纵坐标（方向同纵坐标z）。

非饱和渗流用Richards方程表示，以压力水头为自变量，其偏微分方程如下［25］：

式中：C为比水容量（dθ/dh）；Ss为储水率也叫贮水率，1/m；θ为体积含水率；Se为有效饱和度；hp为压力水头（p）；Kr为非饱和渗透系数。其中非饱和水力参数C、Se、θ等用Van Genuchten 模型模拟。

Van Genuchten模型其原理表达式如下［26］：

式中：θ为体积含水率；h为负压，m，取正值；θs，θr分别表示饱和体积含水率和残余体积含水率；α、m、n为模型参数。

Kr的表达式为［27］：

式中：Se为有效饱和度；d为孔隙分布的分维。

3 研究区模型构建

为对比分析，本文分别建立考虑裂隙的模型（裂隙流模型）和不考虑裂隙的模型（孔隙模型）进行研究与对比。

3.1 研究区选取与模型生成

本文选取研究区域桩号62+809 位置处的局部渠道断面作为此次的模拟计算区域，区域长高分别为55 和23 m。利用MATLAB 编制算法，以裂隙初始参数为依据，生成裂隙网络模型如图5所示。

图5 随机裂隙网络图Fig.5 Random fracture network diagram

将图5 与渠道断面叠加，并根据2.1.1 节所述假设，对不位于研究区域内的裂隙进行删除和截取；采用三角形网络剖分法进行有限元网格剖分（对研究重点区域进行网格加密），最终得到的裂隙流有限单元网格如图6 所示，裂隙的开度则在COMSOL裂隙流模块中设置。不考虑裂隙流的孔隙模型有限单元网格如图7所示。

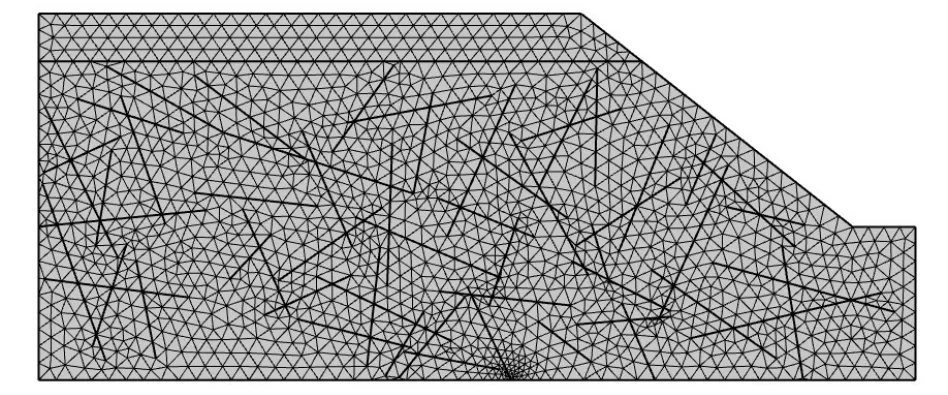
图6 裂隙模型有限单元网格划分Fig.6 Finite element meshing of fracture model

图7 孔隙模型有限单元网格划分Fig.7 Finite element meshing of pore model

3.2 模型相关参数设置

数值模拟采用COMSOL 软件的Darcy 定律模块进行数值模拟。在渗流计算中，采用Darcy 定律匹配Richards 方程作为渗流计算的基本方；非饱和水力参数采用Van Genuchten 模型计算；渗流相关参数采用野外实验并参考原渠道设计渗流参数（见表2）。

表2 相关渗流计算参数Tab.2 Related seepage calculation parameters

3.3 模型边界条件设置

在渗流模型中，上边界与边坡坡面为大气降水边界，左侧设置水头边界。同等地下水位时渠道不输水时扬压力最大，为最不利工况，因此渠道底部设置为无流动边界。右侧按年庚乾［28］研究的渗流边界设置（如图8 所示），即当边坡体内非饱和时，水不会向外渗出；当边坡体内达到饱和时，水则不断向外渗出，渗流边界方程可表示为：

式中：n表示边界外的法向量；u表示边界的流速；ρ为液体密度；Ks为岩体饱和渗透系数；p为孔隙水压力；L为耦合长度尺度（近似代表渗流边界厚度）。

4 渠道边坡渗流模拟及结果

4.1 不同降雨条件下模拟

在2013 年7 月，莱州连续降雨5 d，累计市平均降雨量达到500 mm 以上；在2022 年由于烟台地区受第12 号台风“梅花”影响，9 月14 日6 时-16 时，烟台市发生一次强降水过程。据市水文中心统计，全市平均降水量208.7 mm，最大点为蓬莱区村里集镇南官山站490.5 mm。因此本次模拟参考这两次极端降雨的时段平均降雨量作为降雨过程。固定地下水水位（9.6 m），设置降雨强度分别为5 和20 mm/h，降雨时长分别为96 和24 h，并且在降雨停止后继续模拟40 h的入渗时长（见表3），采用COMSOL 软件分别构建孔隙模型和裂隙模型，采用Darcy 渗流模块模拟，模拟方案如表3所示。

4.1.1 体积含水率随降雨的变化过程

在自然界的渠道边坡中，地下水位线以下的土体均处于饱和状态，地下水位线以上的部分即为非饱和土体，并且含水率会随着高程的增加而减少。对表3 中的4 种工况分别进行模拟，得到不同降雨强度条件下孔隙模型和裂隙模型在不同时刻的体积含水率分布图。图9 为初始时刻体积含水率图，即深红色部分为地下水位以下部分，图10、图11为雨强为20和5 mm/h不同时刻的体积含水率分布图。

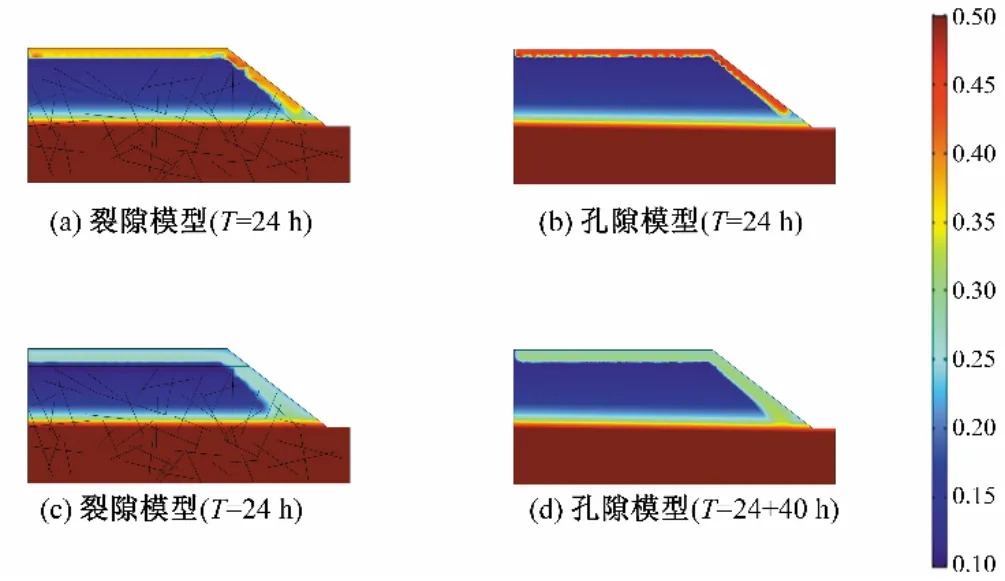
图10 降雨强度20 mm/h下的模型体积含水率（地下水位9.6 m）Fig.10 Model volumetric moisture content at rainfall intensity of 20 mm/h（The water table is 9.6 m）

图11 降雨强度5 mm/h下模型体积含水率（地下水位9.6 m）Fig.11 Moisture content of model volume under rainfall intensity of 5 mm/h（The water table is 9.6 m）

从模拟结果可以明显看出，图10 所示为降雨强度20 mm/h时，当降雨时长T=24 h 时，孔隙模型的湿润峰最低点高程为12 m，而裂隙模型的湿润峰最低点高程为11.5 m；此时孔隙模型入渗区体积含水率达到0.45 以上，裂隙模型入渗区体积含水率仅有0.35～0.4 左右。当降雨停止继续入渗40 h 后，两模型的入渗面积均达到最大，同时部分入渗水补充地下水，裂隙模型的入渗区体积含水率维持在0.25 左右，孔隙模型的入渗区体积含水率维持在0.3。

图11 表明，降雨5 mm/h 的条件下，当T=96 h 时裂隙模型的湿润峰运移速度比孔隙模型要快（裂隙模型湿润峰最低点11 m，孔隙模型湿润峰最低点11.6 m），此时裂隙模型入渗区体积含水率在0.3，而孔隙模型入渗区体积含水率在0.35；当降雨停止继续入渗40 h 后，两模型的入渗面积均达到最大，同时部分入渗水补充地下水，裂隙模型的入渗区体积含水率维持在0.25左右，孔隙模型的入渗区体积含水率维持在0.3。

对比孔隙模型和裂隙模型，可以看出，降雨强度一定情况下，两种模型的湿润峰运移速度有明显的不同，裂隙模型的湿润峰会比孔隙模型快，即时间相同时，湿润峰深入深度更大，易造成地下水位的上涨。裂隙模型的体积含水率略小于孔隙模型；这是因为裂隙的存在，雨水进入裂隙后迅速下渗，入渗深度增加较快，同时裂隙内的入渗水量随着裂隙下渗至地下水位，部分水分补充地下水导致入渗区内的体积含水率略小于孔隙模型。

模拟同时表明，降雨强度的改变对两模型的入渗区域的体积含水率影响较大，入渗区体积含水率与雨强呈正比。

4.1.2 边坡内水压力模拟结果分析

在自然情况下的降雨入渗会造成边坡内水压力的变化，特别是坡脚处水压力的变化容易造成渠道衬砌板鼓胀和脱落。本节选取表3 中工况1、2，针对裂隙的存在与否对边坡内部水压力变化的影响进行数值模拟，得到结果如图12-14所示。

图12 初始条件下边坡内水压力分布云图（地下水位9.6 m）Fig.12 Distribution cloud diagram of pressure in slope under initial conditions（The water table is 9.6 m）

图13 裂隙模型降雨20 mm/h边坡内及坡脚处水压力分布云图（地下水位9.6 m）Fig.13 Cloud image of water pressure distribution in slope and foot of slope with 20 mm/h rainfall in fracture model （The water table is 9.6 m）

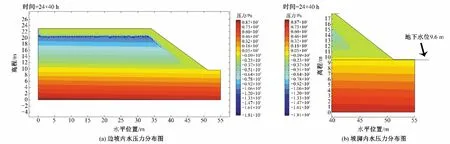
图14 孔隙模型降雨20 mm/h边坡内及坡脚处水压力分布云图（地下水位9.6 m）Fig.14 Cloud map of water pressure distribution in the slope and at the foot of the slope with rainfall of 20 mm/h for pore model（The water table is 9.6 m）

图12所示为两种模型初始时刻水压力分布云图，地下水位以下的压力值呈现大于0 的数值。图13（a）是采用裂隙模型在降雨强度为20 mm/h、降雨历时为24 h 的下渗过程模拟40 h（降雨过程24 h、持续入渗40 h）得到的水压力分布云图；图13（b）为坡脚处水压力分布的局部放大图。图14（a）、图14（b）采用孔隙模型模拟24 h+40 h 的边坡水压力分布云图和坡脚处水压力分布的局部放大图。可以看出，在降雨下渗过程结束后，裂隙模型其压力分布图中部分区域的等值线呈现凸起，这说明此时地下水位已经上升至凸起部位（高程12 m处），而孔隙模型这种现象则不明显。这是由于裂隙模型的湿润锋提前到达地下水位，补充地下水位，易导致地下水位提前上涨，而孔隙模型的湿润峰运移速度比裂隙模型慢，地下水位上涨滞后于裂隙模型。但随着地下水位的上升可能会导致衬砌板附近的压力值会变大，从而对衬砌板产生一定的影响破坏。

4.2 衬砌板所受压力分析

研究区此渠段自通水以来，渠道受扬压力影响衬砌板遭到破坏，其破坏形式主要表现为塌板、鼓板以及脱落。衬砌的破坏导致渠道的输水能力下降，严重影响工程安全运行。为研究渠道衬砌板受压情况的变化情况，选取正常地下水水位情况（地下水位9.6 m），对孔隙和裂隙模型的衬砌板压力情况进行对比分析。

若判断衬砌板所受压力是否达到安全压力值，首先应先对安全压力值进行计算判断，衬砌板抗浮稳定性系数可表示为：

按照最不利情况进行计算：检修期时假设衬砌板顶面水压力为零，水压力直接作用于衬砌板底面，此时采用混凝土衬砌板的饱和容重25 kN/m3，衬砌板厚度为0.06 m，查阅规范可知，当安全系数满足Kf≥1.05 时，得出Δh≤0.14 m（即安全压力最大值为1.4 kPa）。

取地下水位为9.6 m，根据COMSOL 模拟结果，可得到衬砌板所受压力如图15、图16 和表4 所示。图中横坐标X=46.75 m至X=51 m 为渠道衬砌边坡，X=51 m 至X=55 m 为渠道衬砌底板。

图15 降雨强度20 mm/h下衬砌板压力变化曲线Fig.15 Pressure curve of lining plate under rainfall intensity of 20 mm/h

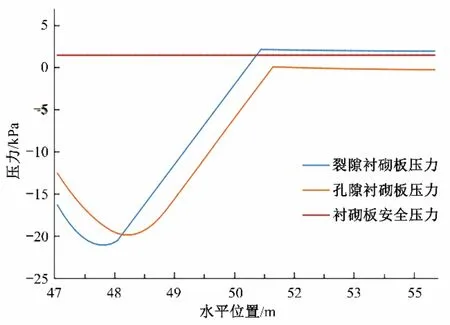
图16 降雨强度5 mm/h下衬砌板压力变化曲线Fig.16 Pressure change curve of lining plate under rainfall intensity 5 mm/h

表4 衬砌板所受压力分析表Tab.4 Pressure analysis table of lining plate

由图表分析，可以看出对于存在裂隙的渠道，其裂隙的存在会对边坡衬砌板的安全有影响。同一次降雨，裂隙模型的衬砌板压力出现最大值处始终提前于孔隙模型，且最大值始终大于孔隙模型，这说明了裂隙的存在使得衬砌板的破坏不仅时间上提前也会发生空间上的扩大。当降雨条件改变时，可以看出高雨强条件下破坏位置比低雨强条件下偏左了0.6 m 左右，说明强降雨条件下衬砌板破坏的范围更广。