库水可压缩性对重力坝动力特性和地震响应的影响
2021-04-29刘明志杜成斌孙立国
刘明志 杜成斌 孙立国
(河海大学 力学与材料学院,南京 211100)
重力坝作为重要的挡水建筑物,强烈地震会给大坝与库水区带来严重的破坏后果.影响大坝地震响应的因素很多,其中水体与坝体间的动力相互作用是一个非常重要的方面[1].
早在1933年,美国学者Westergaard[2]对刚性直立坝面的动水压力进行了开创性的研究,提出了不考虑库水可压缩性的附加质量模型,诸多学者对这一模型在试验和数值模拟方面做了大量的研究[3-5].虽然这一模型能够很好地模拟坝水相互作用,反映出一定的动水压力的本质特征,但是附加质量模型过于理想化,主要是未计入坝体的弹性变形和库水的压缩性影响,这是不符合实际情况的,不能真实地反映坝体-库水相互作用问题.在坝水相互作用的过程中,是否需要考虑库水可压缩性的影响一直是一个有争议的问题,近年来,众多学者对这一问题做了大量的研究.1972年Selby A.等[6]建立了由混凝土材料组成的库水系统,使用钢丝网水泥墙布置压力传感器测量动水压力,实验结果表明,在忽略库水可压缩性时,实验所得的动水压力值与不考虑压缩性时的拉普拉斯方程解较为一致,表明不考虑库水可压缩性更能反映实际情况.但Chakrabarti和Chopra[7-8]在研究重力坝-库水相互作用时指出,是否考虑库水可压缩性与外界激励频率有关,当激励频率比坝体第一阶频率小得多时,可以不考虑库水可压缩性的作用;当外界激励频率较大时,水体的可压缩性对结果有较大的影响.王毅等[9]研究了考虑坝体、库底柔性时库水可压缩性对于坝面动水压力的影响,计算结果表明不考虑库水可压缩性时,坝面所受到的动水压力与地震动激励的频率无关.在考虑库水可压缩性时,在低频阶段,坝体柔性能够增大系统的响应,相反在高频阶段其能降低系统响应;王铭明等[10]建立了5种不同高度重力坝的坝体-库水流固耦合模型,研究重力坝在地震作用下的地震响应,结果表明流固耦合作用会导致重力坝坝面动水压力呈上部偏大、下部偏小的趋势.吴超[11]建立了拱坝-地基-库水系统非线性耦合分析模型,考虑不同库水模型模拟地震动水压力,结果表明动水附加质量模型比可压缩库水模型计算得到的拱坝响应偏大,具体表现为拱坝横缝开度增加,上下游位移极值增加,坝体应力值较大,计算结果偏于保守.李渤等[12]使用有限元模拟了可压缩库水对于坝体动力特性的影响,结果表明可压缩库水相较于空库模型明显降低了坝体的自振频率,且可压缩库水模型自振频率低于不可压缩库水模型自振频率.
本文采用ABAQUS中的声学单元模拟库水,在对库水单元模型充分验证的基础上,以Koyna重力坝为例建立了坝体-库水-地基流固耦合模型,探讨了库水可压缩性对大坝动力特性和地震响应的影响,并探讨了不同坝高和不同卓越频率的地震荷载对重力坝动水压力的影响.
1 流固耦合方程及算例验证
1.1 库水有限元耦合模型
基于无旋、无黏和均质的假定,可以得到以压力为未知量的波动方程:

式中:∇2为拉普拉斯算子;p为动水压力;c为水中声速.
图1为简化坝体-库水-地基力学模型.满足上式的边界条件为:
S1:流固耦合面,满足应力连续边界条件

式中:n为坝库交界面法线方向;ρ为流体密度;an为加速度.

图1 坝体-库水-地基力学模型
S2:底面,采用吸收边界条件

式中:m为库水底面法线方向;q为边界阻抗系数;α为库底反射系数,其范围为[0,1].当α=0时,表示库底为全反射状态;当α=1时,表示库底为完全吸收状态.
S3:无限远处,采用无反射边界条件

式中:l为库尾无限远处法线方向.
S4:自由表面处,无压力作用,不计表面波影响

考虑库水可压缩性时结构位移和流体速度势组成的混合未知量的有限元方程为:

式中:Ms、Ks、Fs分别为与结构有关的质量、刚度和荷载矩阵;Mp、Kp分别为与流体有关的质量、刚度矩阵;Q为流固交界面上的耦合矩阵;Q1、Q2分别为与流体流速相关的耦合矩阵分别为结构加速度、速度、位移分别为流体加速度、速度、位移.
1.2 模型验证
1.2.1 算例1:刚性坝体
为验证声学单元模拟库水的正确性,建立上游坝面竖直的坝体-库水模型[13],坝体高180 m,宽15 m,如图2所示.坝体设为刚性,弹性模量取为3.43×1016Pa,假设库水可压缩并忽略其黏性,水中声速c=1 439 m/s,水体密度ρ=1 000 kg/m3.

图2 上游坝面竖直的坝体-库水模型
Tasi等[14]于1990年基于半解析解提出了一种有效的时域分析方法,考虑到库水的可压缩性,得到了适用于坝体-库水相互作用的动水压力公式:

式中:λk=(2k-1)π/2H,H为水体高度;J0为第一类贝塞尔函数;an和c同前.
定义无量纲的动水压力为:

对模型施加地面斜坡加速度如图3所示,取a=0.2g,研究其动水压力分布,将结果与解析解进行对比.当水体动水压力在底部达到峰值时,绘制坝体表面上的动水压力包络线分布如图4所示,其与解析解吻合较好.绘制坝踵位置动水压力时程曲线如图5所示,与解析解对比,在2 s前曲线趋势较为一致;在2 s后,不同长度的库水区域对于动水压力有一定的影响,随着库水区域的增大,无量纲动水压力最小值逐渐增大,但整体趋势接近相同.

图3 地面斜坡加速度

图4 坝面动水压力包络线比较

图5 坝踵处动水压力时程曲线
1.2.2 算例2:柔性坝体
此时,上游坝面竖直的坝体-库水有限元模型仍如图1所示,施加地震荷载EL Centro如图6所示.坝体弹性模量取为3.43×1011Pa,密度为2 400 kg/m3,泊松比为0.假设库水可压缩并忽略其黏性,水体区域长度取为900 m[13],水中声速和水体密度同前.将计算结果与Lee[15]和Tasi[16]于1991年提出的柔性坝体-库水相互作用的时域解析解进行对比,绘制坝踵位置动水压力时程曲线如图7所示,图中纵坐标为无量纲动水压力,可见整体趋势与解析解较为一致,无量纲动水压力峰值接近相同.因此采用声学单元模拟库水是合理的.

图6 南北向EL Centro地震时程曲线

图7 坝踵坝面动水压力比较
2 库水压缩性对Koyna重力坝动力特性的影响
2.1 工程概况及计算模型
本文以印度Koyna大坝为例进行计算,Koyna坝为混凝土重力坝,位于印度西南部,最大坝高103 m,坝底宽度为70 m.坝体剖面图如图8所示,坝体-库水-地基系统有限元网格模型如图9所示.水体区域向上游取3倍坝高,坝基深度取2倍坝高,地基向下游延伸2倍坝高,地基按无质量考虑[17].模型共有6 923个结点、6 632个单元.其中坝体、坝基采用CPS4R4单元,即4结点减缩单元,共计4 832个;库水采用AC2D4声学单元,共计1 800个.

图8 Koyna重力坝坝体剖面图

图9 Koyna重力坝-库水-地基系统有限元模型
水体表面不考虑表面波作用.水体截断边界设置为吸收边界(无反射平面),不考虑地震波在库尾方向上的返回波.对于坝体-库水和地基-库水之间的接触面,均使用ABAQUS中的TIE进行约束,以模拟接触面之间的耦合作用.
2.2 计算工况及材料属性
建立了3种有限元数值模型:①不考虑坝前库水作用,即空库模型;②满库可压缩库水模型;③满库不可压缩库水模型.当考虑水体可压缩性时,体积模量取为2.07 GPa,当不考虑水体可压缩性时,库水的体积模量取为2.07×1020Pa[18],库水满库水位深度取为90 m.在计算中,坝体混凝土材料、坝基部分均采用弹性模型.坝体动弹性模量为31.03 GPa,密度为2 643 kg/m3,泊松比为0.167;坝基弹性模量取为20 GPa,泊松比为0.25;水体密度取为1 000 kg/m3,考虑库水可压缩性时,水中声速取为1 439 m/s.本文采用Rayleigh阻尼理论[19]来反映混凝土的阻尼,阻尼比取为5%.
计算时采用Koyna实测地震波作为输入地震荷载,地震波时程曲线如图10所示.Koyna地震波地震总时程为10 s,时间间隔0.02 s,地震加速度峰值为0.5g.

图10 Koyna地震波加速度时程曲线
2.3 库水压缩性对大坝自振频率的影响
对比不同模型坝体第一阶自振频率,空库模型的第一阶自振频率最大,为2.48 Hz;不可压缩库水模型第一阶自振频率次之,为2.25 Hz;可压缩库水模型第一阶自振频率最小,为2.18 Hz.考虑库水可压缩性时坝体自振频率略低于忽略库水可压缩性的坝体第一阶自振频率,降幅为3.1%,可见库水的可压缩性对坝体自振频率有一定的影响.
绘制3种有限元模型的前8阶频率如图11所示.
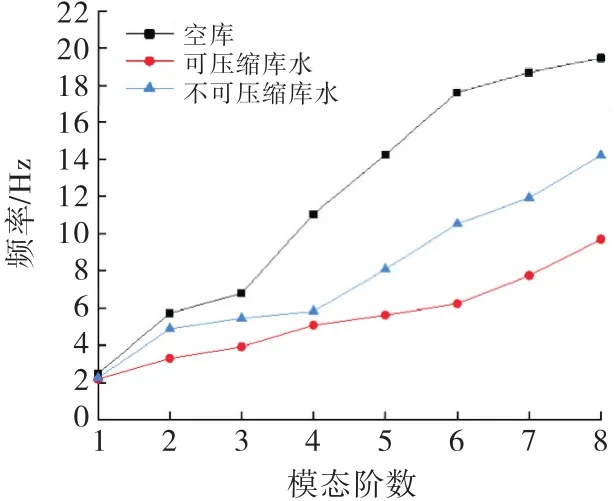
图11 3种不同模型的前8阶频率
由图11可见,前8阶频率空库模型的频率最大,可压缩库水模型频率低于不可压缩库水模型;3种模型低阶频率相差不大,但随着模态阶数的增加,对高阶频率影响较为明显;考虑库水可压缩性模型坝体频率相较于不考虑库水可压缩性模型坝体频率下降约3.1%~34.9%,可见库水可压缩性对坝体动力特性有一定的影响,且在4阶模态后随着模态阶数的增加,相对下降幅度逐渐增大,因此在进行流固耦合计算时不能忽视库水可压缩性对于坝体与库水之间相互作用的影响.
3 库水可压缩性对大坝地震响应的影响
3.1 库水可压缩性对坝体位移响应的影响
对于103 m坝高模型,在Koyna地震荷载下,选取坝顶A点、下游坝面折点B点两个关键部位(见图8),绘制其水平位移时程曲线如图12所示.由图12可知,两种模型的水平位移时程曲线较为一致,水平位移峰值出现位置相同.

图12 关键部位水平位移时程曲线对比
选取坝顶A点、下游坝面折点B点两个关键部位(见图8),其水平位移峰值见表1,可见由于地震对坝体顶部的放大作用,使得其顶部地震动位移较大,下游坝面折点位置水平位移略小.相较于不可压缩库水模型,当考虑库水可压缩性时,所选取特征点水平位移峰值均大于不可压缩库水模型.坝顶位置可压缩库水模型水平位移峰值相较于不可压缩库水模型增大约8.8%、下游坝面折点增大约5.8%.因此考虑库水可压缩性时会增大坝体的水平向位移.

表1 坝体关键部位水平位移峰值 (单位:mm)
3.2 库水可压缩性对坝体应力响应的影响
对于103 m坝高模型,在Koyna地震荷载下,选取坝体关键部位下游坝面折点B点、坝踵D点(如图8所示),在地震作用下主拉应力峰值见表2.

表2 坝体关键部位主拉应力峰值
由表2可知,最大主拉应力出现于坝踵处,且大于下游坝面折点处主拉应力峰值.应该注意到坝踵位置出现了一定程度的应力集中,是抗震薄弱部位,在重力坝设计中应该得到重视.可压缩库水模型相较于不可压缩库水模型会增大主拉应力响应,下游坝面折点处增大幅度约为3.2%,坝踵处增大幅度约为5.2%.
4 不同大坝高度、不同地震卓越频率对大坝动水压力的影响
4.1 不同大坝高度对动水压力的影响
为研究可压缩库水对不同高度大坝动水压力的影响,在保持坝体上下游坡度不变的情况下分别按0.7、1.0、1.3、1.6的比例建立了大坝高度分别为72 m、103 m、134 m、164 m流固耦合模型,库前水位分别为63 m、90 m、117 m、144 m.地震波仍然采用前述的Koyna地震波.图13为4种不同大坝高度的坝面动水压力峰值沿高程的变化曲线,可见库水可压缩性模型动水压力均大于不可压缩库水模型.72 m坝高时,动水压力峰值出现在坝高约39.8%处;103 m坝高动水压力峰值出现在坝高约51.0%处;134 m坝高动水压力峰值出现在坝高约41.6%处;164 m坝高动水压力峰值出现在坝高约43.9%处.可见坝面动水压力峰值出现在上游坝面中部位置,而不是在坝踵位置.

图13 4种不同大坝高度坝面动水压力峰值
表3给出了不同高度大坝动水压力峰值,由表3可见72 m坝高动水压力峰值为0.08 MPa;103 m坝高动水压力峰值为0.19 MPa;134 m坝高动水压力峰值为0.36 MPa;164 m坝高动水压力峰值为0.43 MPa.对比不同高度大坝动水压力,坝面动水压力峰值随着大坝的增高而逐渐增大;库水可压缩性对动水压力有一定放大作用,4种工况下动水压力峰值相较于忽略库水可压缩性时增幅分别约为14.3%、18.8%、20.0%、13.2%.可见库水可压缩性在坝水相互作用时对动水压力有较大的影响,在计算中不能忽略.

表3 不同高度大坝动水压力峰值 (单位:MPa)
4.2 地震激励频率对动水压力的影响
根据畑野正[20]对于库水可压缩性的研究,动水压力与地震输入频率是紧密相关的.本文对103 m坝高模型,选取Kocaeli、EL Centro、Trinidad
3条典型地震波,探究不同地震激励频率对于动水压力的影响.Kocaeli、EL Centro、Trinidad地震波卓越频率分别为0.29 Hz、1.79 Hz、2.76 Hz,加速度峰值取为0.35g,其水平方向地震时程曲线和频谱幅值如图14所示,竖直方向地震波取水平方向的2/3.

图14 3种地震波加速度时程曲线以及频谱幅值
对于可压缩库水模型,选取上游坝面中部C点、坝踵D点两个位置(见图8),绘制其动水压力时程曲线分别如图15、16所示.当地震卓越频率小于可压缩库水模型一阶频率(2.18 Hz)时,上游坝面中部、坝踵处的动水压力是最小的;当地震卓越频率远大于可压缩库水模型基频时,动水压力会略大于上一种情况动水压力;当地震卓越频率和可压缩库水模型基频相接近时,上游坝面中部、坝踵处动水压力是最大的,此时地震荷载对动水压力的影响最为明显.

图15 上游坝面中部动水压力比较

图16 坝踵动水压力比较
表4给出了考虑库水可压缩性时和忽略库水可压缩性时,在不同地震荷载下上游坝面中部C点、坝踵D点位置(见图8)的动水压力峰值.

表4 坝体关键部位动水压力峰值
可见当地震波卓越频率和可压缩库水模型一阶频率(2.18 Hz)相接近时,考虑库水压缩性与不考虑库水压缩性坝体动水压力峰值差别是最大的,考虑库水的压缩性时上游坝面中部位置动水压力峰值相较于忽略库水可压缩性增大约81.8%,坝踵位置增大约75.0%;当地震卓越频率小于和大于可压缩库水模型基频时,两种情况下库水可压缩性对动水压力峰值的影响并不明显.由于地震波是一个随机波,在传播的时候没有固定的频率,所以在计算地震荷载下作用于坝体的动水压力时,不能忽视库水可压缩性的影响,尤其当地震卓越频率与库水基频相接近时,库水可压缩性对于动水压力的影响更为显著.
5 结 论
本文采用ABAQUS中的声学单元模拟库水,研究了库水可压缩性对于坝体动力特性、地震响应和动水压力的影响,得出了以下结论:
1)库水对于坝体自振频率影响显著,库水区域的增加降低了坝体的自振频率,其中可压缩库水模型自振频率略低于不可压缩库水模型自振频率.
2)考虑库水可压缩性时,相较于忽略库水可压缩性会增大坝顶、上游坝面中点等位置的水平位移响应,并且会增大下游坝面折点、坝踵位置的主拉应力响应.
3)对比不同高度大坝模型,动水压力随着大坝高程的增加逐渐增加,坝面动水压力峰值出现于上游坝面中部位置附近;可压缩库水模型相较于不可压缩库水模型会增大坝前动水压力,在计算中不能忽略库水可压缩性的影响.
4)对比不同卓越频率地震荷载下的动水压力,当地震卓越频率与可压缩库水模型自振频率相接近时,可压缩库水模型相较于不可压缩库水模型,在坝踵、上游坝面中部的动水压力峰值相差最为显著,库水可压缩性对动水压力有一定放大作用.
