泵站从长距离明流隧洞引水的水力过渡过程

李甲振，王 涛，郭永鑫，薛兴祖，纪昌知

（1. 中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038； 2. 吉林省水利水电勘测设计研究院，吉林 长春 130021； 3. 中国三峡建工（集团）有限公司，浙江 杭州 310052）

0 引 言

长距离调水是优化水资源空间配置、缓解局部地区或农业灌溉水资源短缺的工程措施，输水方式一般有管、涵、隧有压和渠、隧无压两种［1］。一般情况下，调水工程沿线会设置若干分水口，通过泵站加压或重力自流方式向城镇、工农业供水，如引汉济渭［2］、滇中引水［3，4］、大伙房水库输水［5］等工程。当计算分水口的水力过渡过程时，多数工程需对干线和支线同时求解，这就会碰到有压、无压输水耦合的问题。

针对有压、无压耦合输水系统的水力过渡过程，一种常见的求解方法是采用明渠非恒定流方程和窄缝法描述管道的有压流。杨开林［6］采用Preissmann 四点隐式差分算法进行求解，并给出了保证计算收敛的措施和方法；刘梅清等［7］则采用特征线方法进行求解，万五一等［8］给出了最优时间步长和管、渠空间步长的确定方法。王衍超等［9］在处理南水北调北京段的明满流耦合问题时，也是采用了窄缝法进行计算。莫铁祥和李国栋［10］针对管流负压工况，提出了一种结合CFL 约束条件的流态判别方式。另一种求解方法则是分别计算有压、无压耦合系统的水力过渡过程，连接处的边界条件进行特殊处理。李占松等［11］区分管渠、渠管两种情形，给出了断面结合处特征线法内边界的处理方式。

对于有压、无压耦合的长距离调水工程，无压输水系统的计算时长一般为数小时至数天，时间步长一般为数秒至数分；有压输水系统考虑特征线方法的计算稳定性和计算精度，时间步长一般小于0.1 s，甚至是0.001 s。如果两者采用同一时间步长，会占用大量的CPU，降低计算效率。因此，有必要对无压输水系统和有压输水系统采用不同的时间步长进行求解。

本文以某长距离调水工程为例，研究给出无压、有压输水系统耦合的求解算法，分析泵站事故断电、正常启动、停机的控制策略和水力特性，供类似工程的水力过渡过程计算参考。

1 数学模型

某调水工程从上游水库引水，通过长224 km的无压隧洞输送至下游水库。无压隧洞底坡为1/4010，断面为马蹄形，尺寸为6.56 m×6.56 m，设计流量为50.0 m3/s。在输水隧洞126 km处，向下开挖稳压调节池，侧向引水进入泵站，设计流量为10.2 m3/s。隧洞底高程为242.20 m，稳压调节池深6.44 m，两侧边坡1∶10，底长30.00 m，顶长158.80 m，与明流隧洞同宽6.56 m［图1（a）］。

图1 工程布置图（单位：m）Fig.1 Structure layout of pump station diversion

侧向引水通过有压隧洞进入闸门井，隧洞长273.00 m，底坡为1/54；断面为圆形，直径为3.00 m。闸门井的顺水流长度为8.00 m，宽度为3.00 m。闸门井后接集管进行分流，两侧对称布置4 根进水管，长度分别为45.00 m、31.00 m；断面为圆形，直径为2.00 m［图1（b）］。

该泵站引水系统包括了无压输水和有压输水，控制方程和求解算法如下。

1.1 控制方程

无压输水系统的控制方程为圣维南方程组，包括连续性方程和动量方程：

式中：A为过流面积，m2；t为时间变量，s；Q为流量，m3/s；x为空间变量，m；q为单位渠道长度的侧向流量，m3/s；β为断面流速分布不均引入的修正系数；g为重力加速度，m2/s；h为水深，m；S0为河床底坡；Sf为摩阻比降，计算公式为：

式中：K为流量模数，；n为糙率；R为水力半径，m。

有压输水系统的控制方程包括运动方程和连续方程：

式中：H为从基准线算起的测压管水头，m；V为管道中平均流速，m/s；f为Darcy-Weisbach 沿程水力损失系数；D为管道直径，m；a为水锤波速，m/s；θ为管轴倾角。

1.2 求解算法

无压输水系统的控制方程组，常采用Preissmann 四点隐式差分法格式求解；有压输水系统的控制方程组，常采用特征线方法进行求解。文献［12-14］均对离散方法、计算程序以及基本的水库、调压塔等边界条件进行了详细介绍，此处不再赘述。数值计算的难点在于，如何联立求解无压输水系统和有压输水系统的水力过渡过程。

在无压输水系统的一个时间步长ΔT内，稳压调节池水深的改变量Δh相对于水泵扬程是一个小量，对有压输水系统的水力过渡过程影响很小，可忽略不计。但管道系统与稳压调节池之间的水量交换，对明流隧洞的水力过渡过程影响较大，必须考虑。因此，本文采用了一种弱耦合的方式进行求解，即，①计算有压输水系统T～T+ ΔT的水力过渡过程，计算步数为N=ΔT/Δt，稳压调节池水位恒定为时间T的数值。② 计算N个Δt时间步长，有压隧洞首断面的流入/流出的流量。将N个流量的平均值作为该节点（岔点）的边界条件，求解T+ ΔT时刻的水位和流量。③ 转入步骤①、②继续求解。

数值求解的计算流程如图2所示。

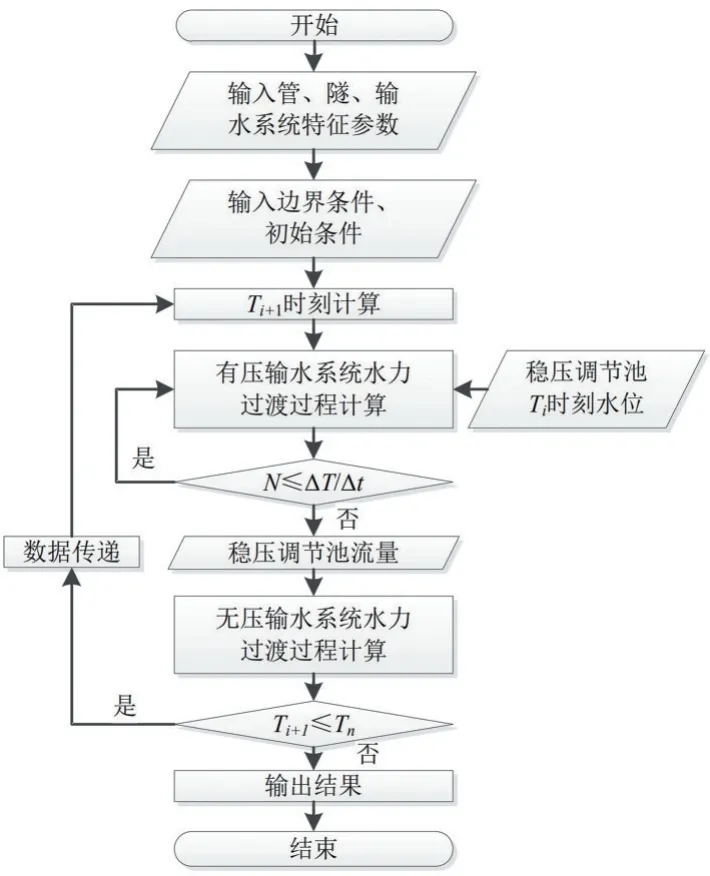
图2 计算流程图Fig.2 Standard calculation procedure

1.3 典型建筑物处理问题

泵站从无压输水隧洞的中间部分引水，通过有压隧洞、闸门井、集管、进水管后进入水泵。工程中的闸门前后均为有压隧洞，规划的功能是截断水流，正常运行时处于全开位置。当发生事故断电、水泵正常启动或停运时，由于闸门井具有自由水面，起到了调压井的作用。因此，闸门井需作为双向调压塔考虑。当水位高于244.60 m 时，调压塔水面面积为3.00 m×8.00 m；当水位为239.60～244.60 m时，调压塔水面面积线性变化。

1.4 模型校验

青草沙水库的原水通过2 根长13 650 m、直径5.5 m 的输水隧洞输送至五号沟泵站前池，继而向下游各用户配水。某次水泵调试运行时，李静毅等［15］观察到配水池异常的水位波动，振幅高达1m。本文对该过程进行了仿真计算，关键参数如表1所示。仿真计算的水位波动、峰谷值和周期与现场实测结果一致，如图3所示，说明模型能够较好地模拟输水系统的水力过渡过程特性。

表1 算例参数Tab.1 Parameters of case study

图3 仿真计算与现场实测对比Fig.3 Comparisons between numerical simulation and field test

2 结果与讨论

2.1 水泵事故断电的水力过渡过程

设计工况下，稳压调节池的上游流量为50.0 m3/s，下游流量为39.8 m3/s，泵站的取水流量为10.2 m3/s。发生事故断电后，水泵出口阀门两段关阀，第一段快关15 s，第二段时间45 s，拐点20%全开度；上游水库的放水流量在100 s内由50.0 m3/s减小为39.8 m3/s。

闸门井水位波动如图4 所示。泵站正常运行时，闸门井水位为246.20 m。事故断电后，水泵出口的阀门两阶段关闭，闸门井水位迅速增加，32 s 达到最高值247.65 m，水位升高0.45 m；之后闸门井水位降低，82 s 达到极小值246.42 m。0～40 h 内，闸门井水位在0～9 h 内振荡上升，9～30 h 内逐渐降低，之后稳定为246.40 m。主要原因是，水库下泄50.0 m3/s、泵站取用10.2 m3/s时，上游126 km 隧洞基本为50.0 m3/s 对应的设计水深4.75 m，下游98 km 隧洞基本为39.8 m3/s 对应的设计水深3.99 m。水泵事故断电、阀门关闭后，泵站停止取水，上游126 km隧洞内的水向稳压调节池及下游输送，致使稳压调节池、闸门井的水位逐渐增加；9 h 后，上游水库下泄水量减小产生的减压波传播至稳压调节池，闸门井水位开始降低。

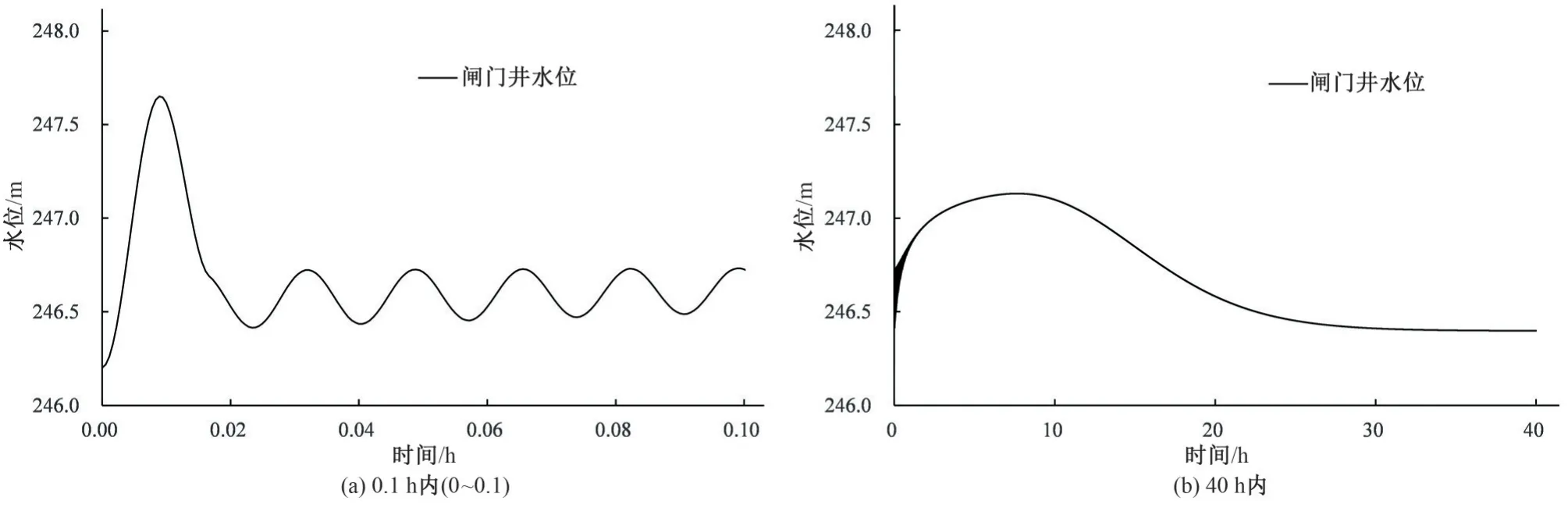
图4 闸门井水位波动Fig.4 Water level variation of gate shaft

稳压调节池上、下游明流隧洞的流量过程如图5 所示。水泵事故断电后，上游水库的放水流量在100 s 内减小，隧洞20、40、60、80 和100 km 处的流量逐渐减小，水位逐渐降低，约22 h后，100 km 处的流量达到40.2 m3/s［图5（a）］。由于水泵出口阀门关闭，侧向引水减小为零，稳压调节池上游隧洞3.99～4.75 m（39.8、50.0 m3/s 对应的设计水深）之间的水体只能输送至下游，致使下游隧洞的流量逐渐增加。当上游水库下泄水量减小产生的减压波传播至相应位置时，流量开始减小［图5（b）］。稳压调节池、下游20 km、下游40 km、下游60 km 和出口的流量最大值分别为49.6、49.3、48.9、48.6 和48.2 m3/s。相对比设计流量39.8 m3/s，40 h内多输送至下游水库的流量为55.2 万m3。

图5 明流隧洞流量波动Fig.5 Discharge variation of free-flow tunnel

稳压调节池上、下游明流隧洞的水位波动如图6 所示。水泵事故断电后，随着阀门两阶段关闭，稳压调节池的水位在36 s（0.01 h）迅速抬升，72 s（0.02 h）升高0.17 m［图6（a）］。稳压调节池侧向分水减小引起的水位增高，致使上游200 m 处水位略降低后增加。与闸门井水位波动类似，0～40 h 内，稳压调节池水位在0～9 h 内振荡上升，9～30 h 内逐渐降低，之后稳定［图6（b）］。数值计算过程中，一个时间步长ΔT=2 s内稳压调节池的最大水位变幅为0.02 m，对有压隧洞水力过渡过程的影响可忽略，这也说明了本文提出的数值计算方法是可行的。

2.2 水泵正常启停的水力过渡过程

水泵正常启动时，输水系统的初始状态为：稳压调节池的上游流量、下游流量均为39.8 m3/s；输水系统的最终状态为：稳压调节池的上游流量为50.0 m3/s，下游流量为39.8 m3/s，泵站的取水流量为10.2 m3/s。经研究给出的控制策略为：上游水库的放水流量在100 s内由39.8 m3/s 调整为50.0 m3/s；三台机组的泵后阀门在20 h开始动作，100 s内线性开启。

阀门未开启时，闸门井水位为246.95 m。阀门开启后，水泵吸水产生的压力波动在稳压调节池、闸门井之间传播，使闸门井水位产生一定的波动，最大值为247.11 m，最小值为246.00 m，振幅为1.11 m［图7（a）］。泵后阀门开启所产生的闸门井水位波动，15 min 后振幅趋于0。0～20 h 内，上游放水增加使闸门井水位增加；20～25 h，闸门井水位逐渐降低，之后趋于稳定水位246.20 m［图7（b）］。

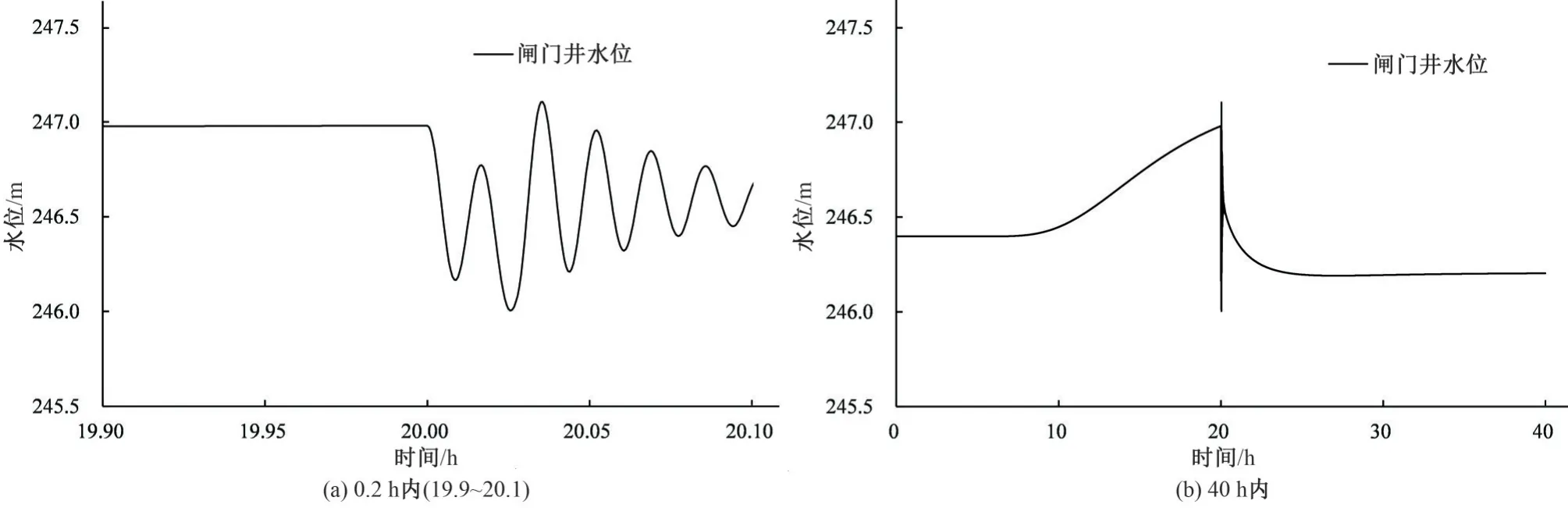
图7 闸门井水位波动Fig.7 Water level variation of gate shaft

上游水库的放水流量增加，隧洞20、40、60、80 和100 km 处的流量逐渐增大，水位逐渐升高，约22 h后，100 km 处的流量达到49.5 m3/s［图8（a）］。阀门开启后，水泵取水，稳压调节池流量迅速减小至设计流量39.8 m3/s。下游20 km、下游40 km、下游60 km 和出口的流量最大值分别为46.9、45.8、45.0 和44.3 m3/s。37 h 后，下游出口流量恢复为40.2 m3/s［图8（b）］。相对比设计流量39.8 m3/s，40 h内多输送至下游水库的流量为17.61 万m3。

图8 明流隧洞流量波动Fig.8 Discharge variation of free-flow tunnel

水泵正常停机时，经研究给出的控制策略为：上游水库的放水流量在100 s内由50.0 m3/s 调整为39.8 m3/s；三台机组的泵后阀门在20 h 后开始动作，第一段快关15 s，第二段时间45 s，拐点20%全开度。其水力过渡过程与正常启动类似，不再赘述。

3 结 论

针对某泵站从长距离明流隧洞中间部分引水的水力过渡过程计算问题，提出了一种弱耦合的求解方式，即，认为连接处的水位在ΔT（无压输水系统的时间步长）内是恒定的，计算有压输水系统N个时间步（N=ΔT/Δt，Δt为有压输水系统的时间步长）的水力瞬变过程，有压输水系统的进出流量影响无压输水系统。给出了水泵事故断电、正常启动和正常停机工况下，泵后阀门、上游水库的控制策略及其对下游水库的影响。

上述工程中，闸门井具有自由水面，前后为长度较短的有压输水隧洞（273.00 m）和进水管（45.00 m、31.00 m），在水力过渡过程中起到了调压塔的功能。虽然命名闸门井，但不能仅作为截流建筑，需具体问题具体分析，还应考虑其调压作用。