具有非惯量负载转矩补偿功能的伺服永磁同步电机控制方法*
2023-09-22刁晓飞王先强
毛 帅, 刁晓飞, 王 晓, 王先强, 周 辉
(1.山东理工大学 电气与电子工程学院,山东 淄博 255000;2.中国计量科学研究院 几何量计量科学研究所,北京 100029;3.中电装备山东电子有限公司, 山东 济南 250101)
0 引 言
永磁同步电机(PMSM)伺服系统的负载一般为转动惯量值固定的惯性负载,对于较为精密的永磁伺服运动系统来说,一般不会有外界扰动,不用考虑外界扰动造成的负载转矩[1-2],比如激光跟踪仪的伺服运动旋转系统。因为负载的重心不是准确地位于旋转轴线上,所以在不同旋转位置上重力会引起不同的负载转矩,如图1所示。

图1 负载重力转矩示意图
图1所示的电机负载在伺服控制中惯量不变,其重力引起的负载转矩随旋转位置不断变化而变化,因此要精确控制该负载旋转运动,需要实现抗扰动控制。目前学者们主要研究了抗阶跃突变式转矩扰动的控制方法[3-4],研究思路是在控制系统中加入扰动观测器,观测出扰动量,从而对其进行补偿[5-8]。当然扰动观测器也可以观测出时变的扰动转矩[9-10],但是观测时一般不考虑黏性阻尼并且由于扰动观测器有观测收敛过程,在电机处于稳定运行状态自转速恒定时观测出的扰动转矩才准确,如果转速不断变化(例如处于伺服运动中),则会造成所观测出的扰动与实际值存在偏差,当该观测扰动加入控制对其补偿抑制时,可能会导致扰动补偿抑制的过冲和不足。针对图1的伺服控制过程,本文在考虑黏性阻尼系数和实时扰动补偿准确性的前提下,设计了一种基于负载辨识的永磁同步电机负载转矩补偿的控制方法。
1 负载转矩辨识
理想伺服旋转系统中,负载质心位于转轴轴线上,因此旋转运动中不用考虑重力引起的负载转矩,但实际上负载质心不可能准确位于转轴上,其与转轴必然会存在一个力臂距离,负载质心与转轴对应的运动学关系如图2所示。

图2 负载质心不位于转轴上对应的运动学关系
伺服电机的运动学方程式为

(1)
式(1)中的负载转矩TL需要按照图2所示替换为不同旋转位置上重力引起的负载转矩,因此可得图2所示的伺服电机运动学方程式为

(2)
式中:Te为电机输出转矩;J为转动惯量;Bm为黏性阻尼系数;ωm为电机的机械角速度;F为负载的重力力矩;θo为负载初始旋转时的位置角度;θm为电机的机械旋转角位移。
若为表贴式永磁同步电机,并满足最大转矩电流比控制时,电机输出转矩表示为
Te=Kt×Iq
(3)
式中:Kt为电机转动常数;Iq为电机的q轴电流。
式(2)中,J、Bm、F和θo为需要辨识的参数,其他参数为已知或可测量。为便于使用拟合方法,将式(2)改写为
Fsinθosinθm=KtIq
(4)
建立如式(4)所示的拟合模型函数式,J、Bm、Fcosθo和Fsinθo为需要辨识的参数。Fcosθo和Fsinθo这两个参数进行平方和运算然后开根号便可得参数F,进行比例运算求反正切角便可得参数θo。给予永磁电机伺服电机系统一组单调递增或递减线性速度命令,便可得到Iq、ωm和θm各自对应的一组测量数据。最后,便可以通过基于模型函数式(4)的非线性回归拟合方法得到四个需要辨识的参数。
这里所用的非线性拟合方法为(Levenberg-Marquardt)方法[11]。其伪代码如下:
Begin
k=0;v=2;θ=θo
H=JTJ;g=JTr

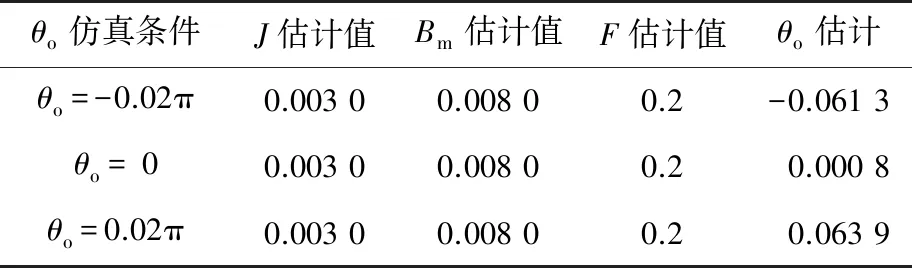
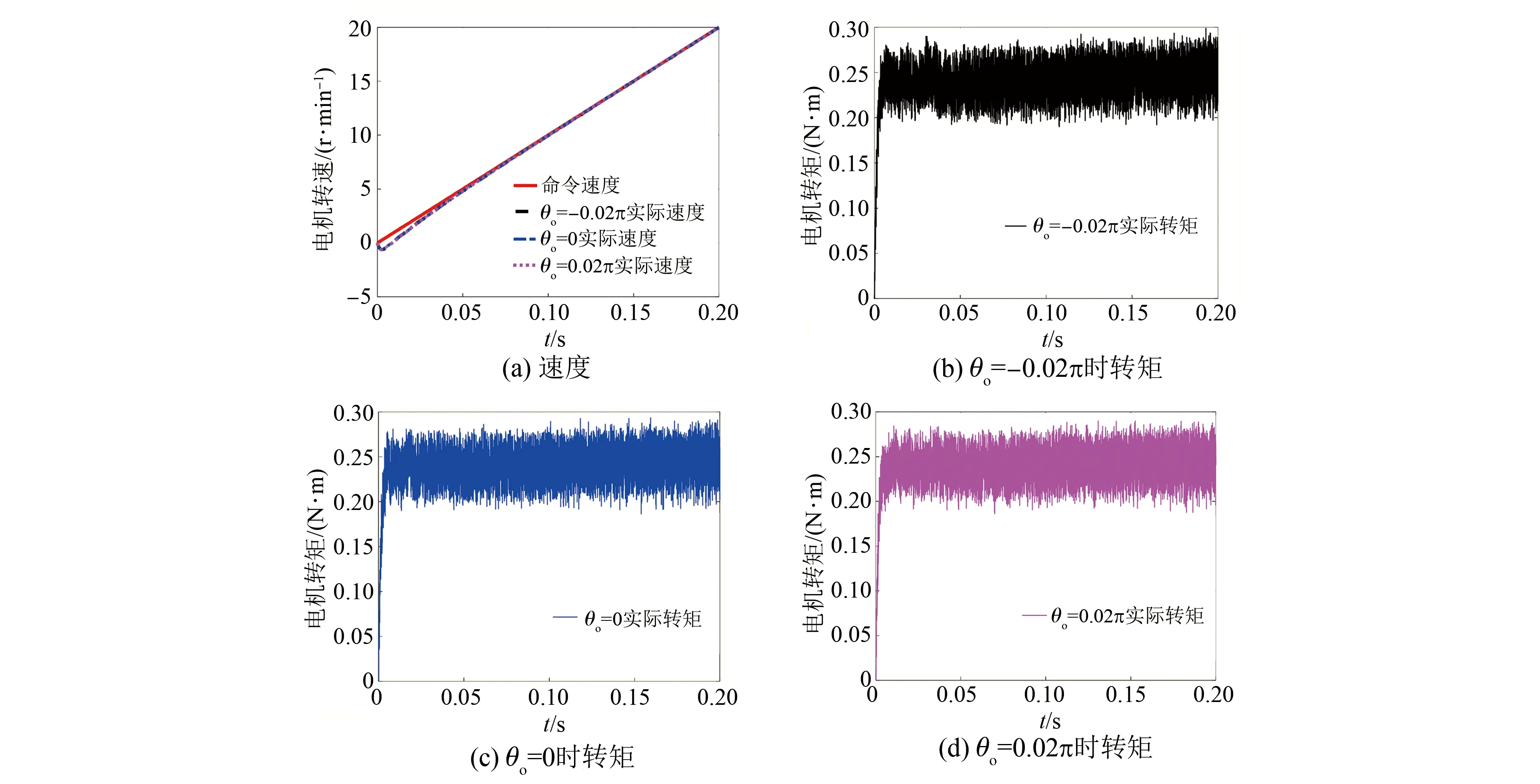
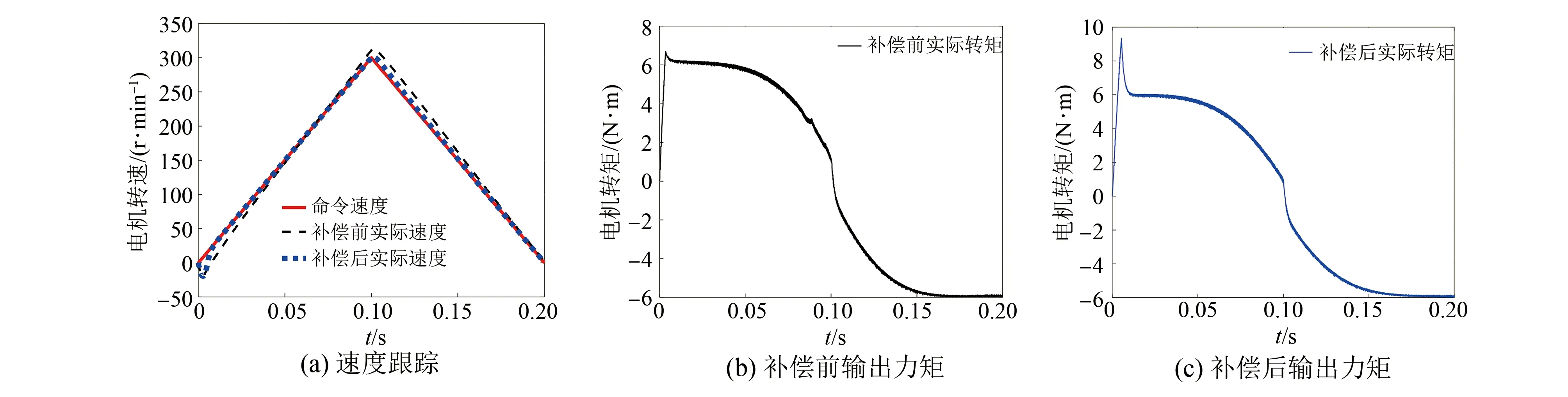
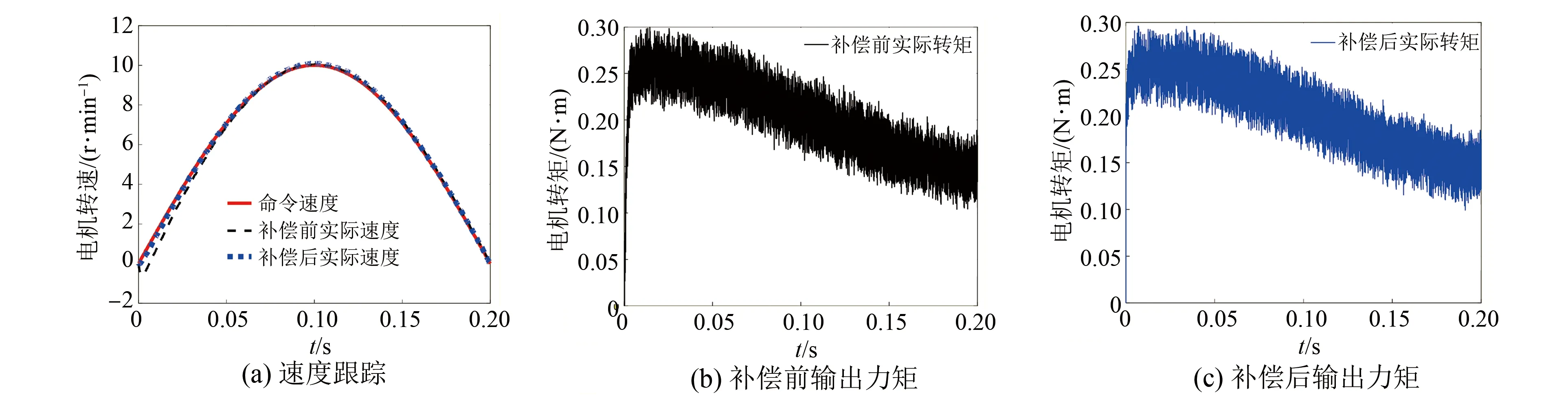
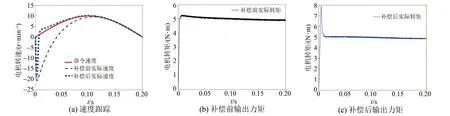
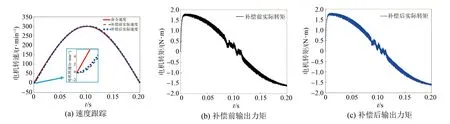
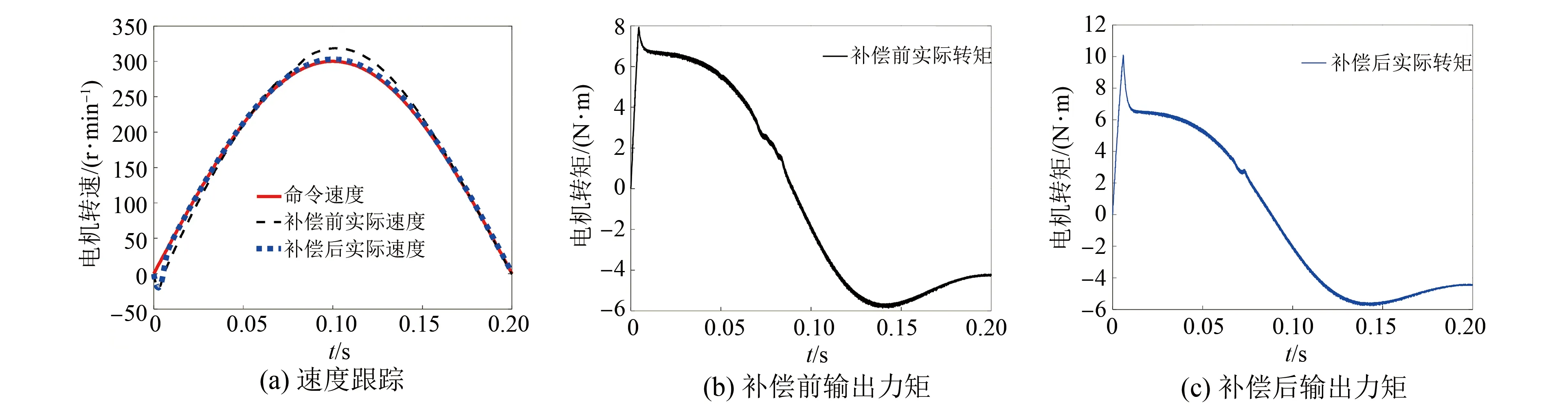
while (notfound) and (k k=k+1; found:=true else θnew=θ+λ ρ=2(F(θ)-F(θnew))/λT(μλ-g) ifρ>0 θ=θnew;H=JTJ;g=JTr v=2 else μ=μ*v;v=2*v End 其中:k为迭代计算次数;τ,1和2分别为微小常量值;hjj为矩阵H的对角元素值;θo是θ的初始估计值。 假设测量的数据组数为m,其组号i≤m,需要辨识的参数为四个,所以参数编号j≤4。每次测量后得到一个向量和一个标量,其表达式为 (5) yi=(KtIq)i (6) θ为需要辨识参数的估计向量,其表达为 (7) 每次测量数据对应的残差ri的表达式为 ri=yi-θTxi (8) 式中:x为残差向量r,r=[r1r2r3…ri…rm]T。 Jacobian矩阵J为m行4列的矩阵,其中每行数据是以θ为自变量的函数行向量表达式: (9) 另外,伪代码中F(θ)可表示为 (10) 经典电机控制即主要通过PI调节的电流环和速度环实现电机的控制[12-13],如图3所示。其中,电流环可以等效为一个一阶惯性环节1/(1+Tis)(Ti为电流环带宽倒数),该等效的前提是不考虑非惯量的负载转矩,并且要求d轴和q轴的电压值是电流完全解耦后的电压值。 图3 电流环和速度环结构框图 电流环d轴和q轴的电流完全解耦可以采用前馈解耦控制策略来实现。不考虑非惯量的负载转矩表达式为 (11) 在实际工程中不能不考虑非惯量的负载转矩对控制的影响,此时需从机械运动学角度来考虑,则需要满足等式: (12) (13) (14) 整体模型图如图3中虚线框模块所示。 整体的控制模型(Simulink模型)如图4所示。其中的(Load torque caused by gravity)和(Load torque estimation)模块输出分别为Fcos(θo+θm)仿真结果和参数辨识后得到的估计值,Load compensation模块输出为参数辨识后的[Bmωm+Fcos(θo+θm)] ×(1+Tis)/Kt。图4中的参数flux、L和Pn分别为磁链、定子电感和极对数,电流环采用前馈解耦控制策略。参数辨识阶段,Load compensation模块输出不用加入到电流环的前端,只使用经典的PI电机控制;负载补偿阶段,Load compensation模块输出加入到电流环的前端。仿真参数设置取值:极对数为4,定子电感为12 mH,定子电阻为0.958 Ω,磁链为0.182 7 Wb (可得电机转动常数Kt=1.096 2),转动惯量J为0.003 kg·m2,阻尼系数Bm为0.008 N·m·s,负载的重力力矩F分别设置为0.2 N·m和5 N·m,电机母线电压为81 V。 图4 具有负载重力转矩补偿功能的整体模型图 仿真θo分别为±0.02π rad和0 rad三种条件下对应的参数辨识结果。给予图4系统的速度命令函数为100 t,通过非线性回归拟合方法辨识重力力矩0.2 N·m和5 N·m条件下的参数,参数辨识对应的速度和输出转矩情况如图5和图6所示,结果如表1和表2所示。 表1 重力力矩0.2 N·m参数辨识结果 表2 重力力矩5 N·m参数辨识结果 图5 力矩为0.2 N·m条件下辨识对应的速度和力矩 图6 力矩为5 N·m条件下辨识对应的速度和力矩 由表1和表2可知,通过回归拟合可以比较准确地辨识出相应参数,除了θo外其他参数都为其仿真值。图7~图14是在三角波和正弦速度函数命令输入情况下负载补偿前和补偿后对应的速度跟踪情况和输出力矩结果(注:三种不同θo值输出情况一致,所以未特意说明结果所对应的θo值)。 图7 力矩为0.2 N·m条件下三角波低速度函数命令输入时速度跟踪情况和输出力矩结果 图8 力矩为5 N·m条件下三角波低速度函数命令输入时速度跟踪情况和输出力矩结果 图10 力矩为5 N·m条件下三角波高速度函数命令输入时速度跟踪情况和输出力矩结果 图11 力矩为0.2 N·m条件下正弦低速度函数命令输入时速度跟踪情况和输出力矩结果 图12 力矩为5 N·m条件下正弦低速度函数命令输入时速度跟踪情况和输出力矩结果 图13 力矩为0.2 N·m条件下正弦高速度函数命令输入时速度跟踪情况和输出力矩结果 图14 力矩为5 N·m条件下正弦高速度函数命令输入时速度跟踪情况和输出力矩结果 由图7~图14可看出,无论是低速还是高速情况下,负载补偿能够比未补偿更好地跟踪速度命令,特别是在初始阶段的初始时刻,输出力矩相对所加初始负载力矩非常小,负载补偿能够使因所加初始负载力矩致使速度产生的负变化更快地变为正值。从整体效果上看,负载补偿控制相较未补偿时能较快地响应所输入的速度命令,因此可以避免速度误差。 本文通过非线性回归拟合方法对电机运动学方程中的负载惯量、黏性阻尼系数、 负载重力力矩和负载初始位置角度等四个参数进行辨识,从而得到非惯量的负载转矩。然后对经典电机PI控制方法中的电流环进行前馈转矩补偿,实现对时变负载转矩的补偿。仿真结果验证了该补偿可使速度响应能较快地跟踪输入的速度命令,避免了较大速度误差的出现。
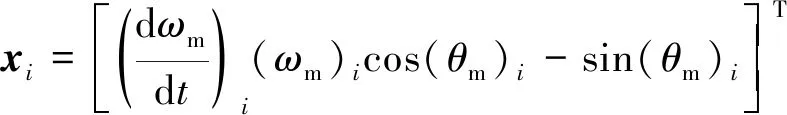
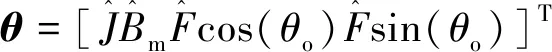
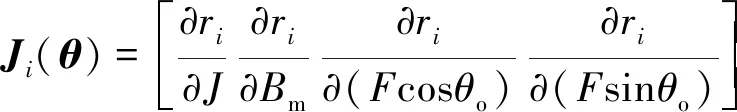
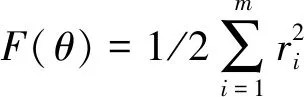
2 负载转矩补偿
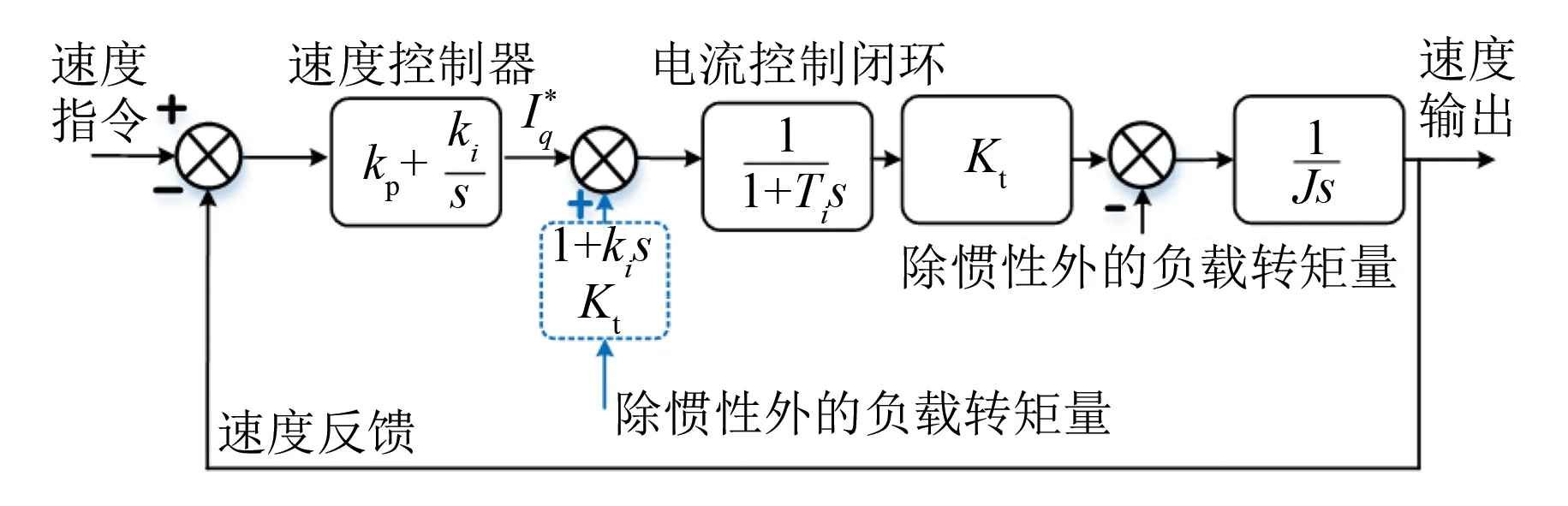
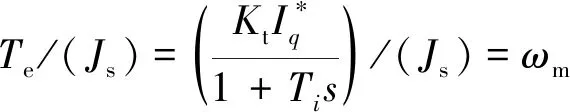
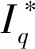
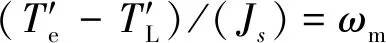
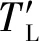

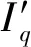
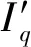
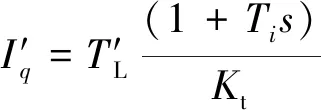
3 仿真分析





4 结 语
