基于时变滤波经验模态分解和SSA-LSSVM的变压器内部机械故障诊断方法*

2023-09-22张甜瑾邵心悦陈子豪吴金利

电机与控制应用 2023年9期

臧旭, 张甜瑾, 邵心悦, 杨嵩, 陈子豪, 吴金利

(1.国网江苏省电力有限公司镇江供电分公司,江苏镇江 212000;2.河海大学能源与电气学院,江苏南京 211100)

0 引言

变压器作为电力系统的关键设备,对保障供电可靠性具有重要意义。然而,随着其投入运行的时间越来越长,变压器内部往往会产生铁心松动等潜伏性机械故障[1],故障一旦累积严重,将会危及电力系统的整体安全。因此,对变压器内部的机械故障进行诊断,对防止电力系统可能发生的危害有非常重要的意义。目前,振动分析法已经被大量运用于变压器铁心或绕组等内部机械故障的检测中,成为当下的研究热点[2-4]。

变压器振动信号是通过吸附于箱体表面的振动传感器采集来获得,该方法实施简单、操作方便,且采集的全过程不会影响变压器的运行状态。变压器铁心受磁致伸缩效应的影响产生振动,而铁心发生松动故障等缺陷时变压器的振动状态必定发生改变[5-6],因此利用振动分析法进行变压器内部机械故障诊断是可行的。

文献[7]利用变压器振动信号频谱变化以辨别铁心与绕组的故障,指出变压器高次谐波分量主要由铁心振动产生,而基频同时受铁心与绕组振动影响,其为判别铁心和绕组等变压器主要故障奠定了理论基础。文献[8]将经验模态分解(EMD)运用于可分离变压器铁心与绕组各自的振动信号中,所得分离信号频谱与正常状态下一致,取得了一定的效果。文献[9]将集合经验模态分解(EEMD)应用于变压器振动、声音信号的模态分量峭度特征提取上,试验结果表明该方法提取出的特征量能够反映时域和频域特征,有利于变压器状态的判定。上述方法均在各自场合实现了一定效果,但是EMD方法本身存在模态混叠的问题, 这会影响信号处理的准确性,EEMD方法虽然引入白噪声减弱了模态混叠的严重程度,但是可能会掩盖掉原始信号的某些信息。虽然目前已有相关改进方法,但是仍存在较多不足。文献[10]提出采用互补集合经验模态分解提取气体绝缘金属封闭输电线路(GIL)机械故障特征的方法,虽然解决了EEMD中白噪声遗留的问题,但仍存在分解过剩的问题。时变滤波经验模态分解(TVFEMD)是在EMD的基础上引入时变滤波技术的一种信号处理方法,该方法能够提高频率分离性能,解决EMD过程中产生的模态混叠问题。

麻雀搜索算法作为新型智能优化算法,具有出色的寻优能力,已成功应用于故障诊断、状态评估和预测等方面。文献[11]采用麻雀搜索算法优化了详尽可能性模型(ELM)的输入权值并隐藏层节点偏置,提高了油浸式变压器故障诊断模型的准确率。

综上所述,本文提出一种基于时变滤波经验模态分解和麻雀搜索算法优化最小二乘支持向量机(SSA-LSSVM)的变压器内部机械故障诊断方法,对变压器铁心不同程度的松动进行诊断识别。首先,采用TVFEMD对振动信号进行分解获取多个模态分量(IMF);然后,选取相关性最优的IMF分量,并计算其样本熵;进一步地,利用所求熵值构建特征向量集;最后,利用SSA优化的LSSVM模型实现变压器铁心内部潜伏性机械故障的诊断。试验结果表明,相较于传统的故障分类模型,所提方法能够更加准确地识别变压器内部的机械故障和不同故障程度。

1 基于TVFEMD的变压器振动信号特征提取

1.1 TVFEMD基本原理

TVFEMD算法设计时充分考虑了EMD方法的不足,其最大特点在于采用非均匀B样条近似作为时变滤波器从而完成筛选过程,同时,充分利用瞬时幅度和频率信息,自适应地设计了局部截止频率[12],TVFEMD方法具体实现过程如下。

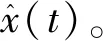
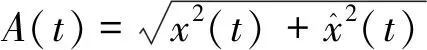
(1)

瞬时相位可表示为

(2)

考虑由N个窄带分量组成的多分量信号可表示为

(3)

式中:am(t)为第m个分量瞬时幅值;φm(t)为相位。

当N=2时,可得:

cos[φ1(t)-φ2(t)]

(4)

a1(t)a2(t)·cos[φ1(t)-φ2(t)])}+

(5)

假设a1(t)和a2(t)的变化速度比cos[φ1(t)-φ2(t)]慢得多,那么当cos[φ1(t)-φ2(t)]= -1时,A(t)取最小值。此时的关系为

cos[φ1(tmin)-φ2(tmin)]=-1

(6)

将式(6)代入式(4)和式(5)中,可得:

Amin(t)=|a1(tmin)-a2(tmin)|

(7)

φ′(tmin)A2(tmin)=

(8)

又由于:

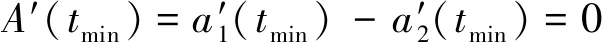
(9)

通过联立式(6)～(9),可解得a1(tmin)、a2(tmin)、φ1(tmin)和φ2(tmin);同理,类似的方法可求得a1(tmax)、a2(tmax)、φ1(tmax)和φ2(tmax)。随后,通过插值可以求得a1(t)、a2(t)、φ1(t)和φ2(t),但求解上述方程十分困难。因此,利用下列方法进行替代,具体为

(10)

因为a1(t)和a2(t)波动较小,所以b1(t)和b2(t)可依次利用A({tmin})和A({tmax})插值得到。假设a1(t)≥a2(t),则

a1(t)=[β1(t)+β2(t)]/2

(11)

a2(t)=[β2(t)-β1(t)]/2

(12)

进一步地,令:

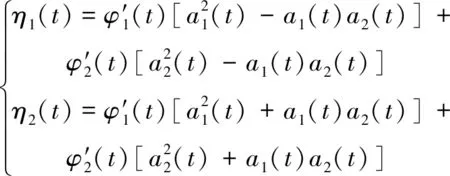
(13)

联合式(5),可得:

η1(tmin)=φ′(tmin)A2(tmin)

(14)

η2(tmax)=φ′(tmax)A2(tmax)

(15)

h1(t)和h2(t)可通过φ′({tmin})A2({tmin})和φ′({tmax})A2({tmax})插值求得。有如下表达式:

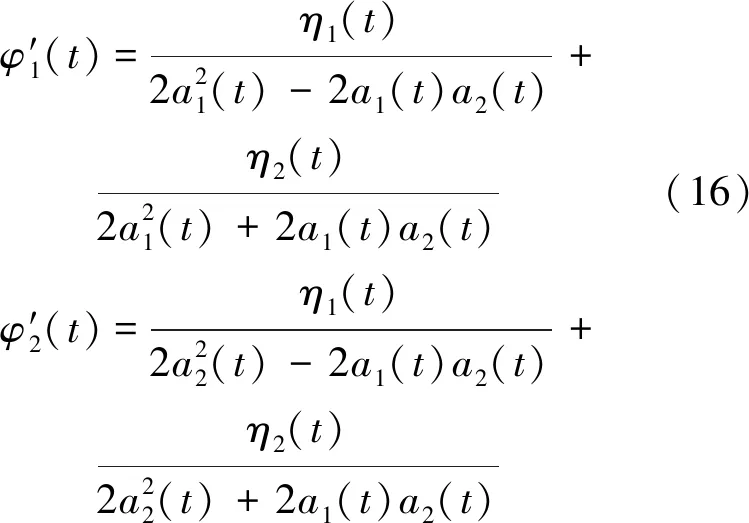
(17)

可得局部截止频率为

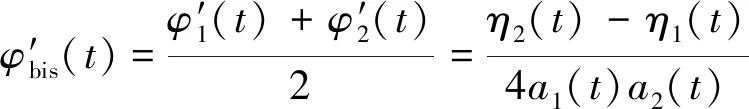
(18)

由此可得:

(19)

对x(t)应用该B样条近似滤波器,即将h(t)极值点作为节点,近似结果为m(t)。该方法设置的终止条件为

(20)

式中:BLoughlin(t)为瞬时带宽;φavg(t)为瞬时平均频率。

当θ(t)≤ξ时,x(t)即为一个IMF分量;否则,将x(t)-m(t)重新按照上述过程进行试验直到符合条件为止。

1.2 相关系数法

相关系数可以衡量分解后的信号与原始信号的相关性,从而剔除相关性较小的信号分量。首先计算原始信号自相关函数与各IMF分量自相关函数的相关系数,然后确定阈值标准,选取相关性最大的IMF分量,从而提高特征向量建立的准确性。相关系数计算表达式如下

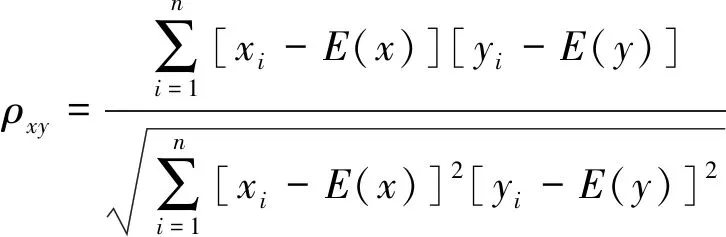
(21)

式中:E(x)、E(y)为两种信号x、y的均值。

相关性最大的阈值标准求解表达式为

(22)

式中:ρmax为相关系数的最大值。

1.3 样本熵

样本熵常用于衡量系统时间序列的复杂度[13]。通过对经TVFEMD后的变压器振动信号的各IMF分量分别计算样本熵,可定量描述每种故障程度下变压器的振动特征。计算样本熵的具体步骤如下。

(1) 将时间序列分为n-m+1个序列:

Xi(t)=[xi(t),xi+1(t),…,xi+m-1(t)]

(23)

式中:m为维数,1≤i≤n-m+1;n为序列数据个数。

(2) 计算dij=max|xi+k(t)-xj+k(t)|,该式表示Xi(t)与Xj(t)中元素距离的最大值,其中0≤k≤m-1。

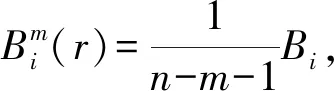
(4) 维数为m+1时,重复步骤(a)～(c)。

(5) 所求样本熵可表示为

SampEn(m,r,n)=lnφm(r)-lnφm+1(r)

(24)

2 基于麻雀搜索算法优化的LSSVM算法

2.1 麻雀搜索算法

麻雀搜索算法(SSA)启发于麻雀觅食与逃避捕食者的行为,是一种新型智能优化算法[14]。下面简要介绍SSA的具体过程。

在麻雀群体中,每只麻雀的行为大致可分为下列情况。

(1) 充当发现者,搜索食物;

(2) 充当跟随者,追踪某发现者;

(3) 侦察危险,若危险则弃食。

假设共有N个麻雀,每次迭代计算的过程中,选取P个位置最优的麻雀作为发现者,其他的(N-P)个则作为跟随者。

在d维解空间中,每只麻雀位置为X=(x1,x2,…,xd)。每代发现者的位置更新公式为

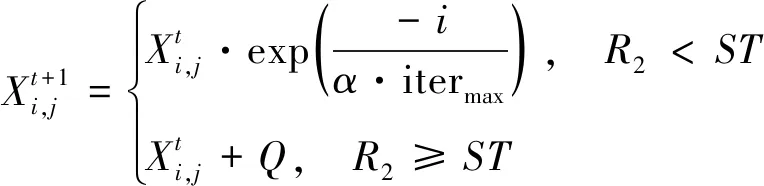
(25)

式中:Xi,j为第i个麻雀第j维信息,j=1,2,…,d;t为当前迭代次数;itermax为最大迭代次数;α∈(0,1];R2∈[0,1]为安全值;ST∈[0.5,1]为预警值;Q为标准正态分布随机数。

每代跟随者位置更新公式为

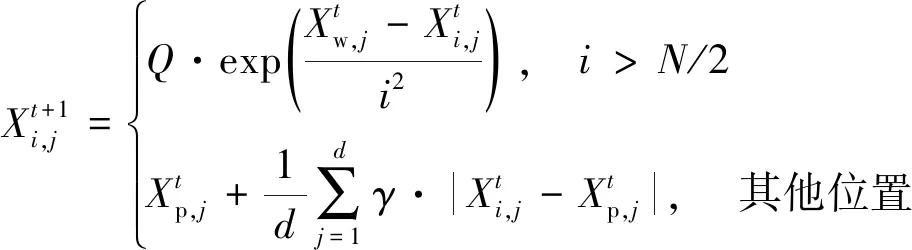
(26)

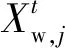
每代中随机选取10%～20%个体意识到危险,位置更新公式为

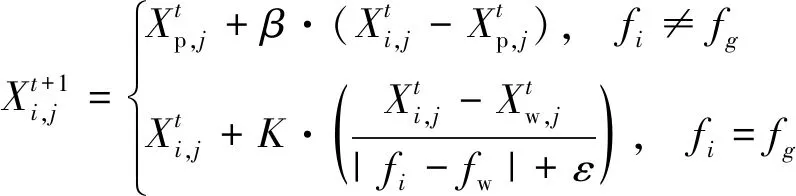
(27)

式中:b为标准正态分布的随机数;K∈[-1,1];e为较小数,防止分母为零;fi为当前麻雀的个体适应度值;fw为最差位置的适应度值;fg为最佳位置的适应度值。

因此,SSA寻优的步骤即先将种群分为发现者和跟随者,再根据式(27)～式(29)更新种群位置,在此基础上更新当前全局最差和最佳个体的位置,在达到最大迭代次数前重复上述步骤,直至最后获得最佳位置。

2.2 SSA-LSSVM诊断模型

LSSVM是一种广泛使用的机器学习算法,主要用于模式分类识别等领域[15-18]。该算法是传统支持向量机(SVM)的一种扩展,其将支持向量机中松弛变量的不等式约束改为等式约束,从而可以通过求解线性方程组的方式来求解LSSVM的值。其中,具有径向基函数(RBF)核函数的LSSVM的两个参数——正则化参数c和核函数参数s对SVM模型的性能影响很大,直接关系到最终的分类精度。因此,本文选择将SSA应用于LSSVM的c、s参数寻优中,以获得最佳的模型识别精度。采用SVM诊断过程中的准确率作为适应度函数可表示为

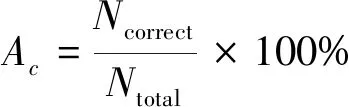
(28)

式中:Ncorrect为识别正确的样本数;Ntotal为全部样本个数。

3 基于TVFEMD和SSA-LSSVM的变压器内部机械故障诊断模型

本文所提基于TVFEMD和SSA-LSSVM的变压器内部机械故障的诊断步骤具体如下。

(1) 采集变压器振动信号,并将振动信号数据分为训练样本数据与测试样本数据两类;

(2) 对原始变压器振动信号进行降噪处理,并利用所提TVFEMD方法对处理后的振动信号进行分解;

(3) 获取分解得到的模态分量;

(4) 利用相关系数法选取与原始振动信号相关性最高的IMF,并求其样本熵值;

(5) 利用步骤(4)所得到的样本熵值构建特征量;

(6) 根据上述步骤(1)～步骤(5)分别得到训练样本与测试样本的特征向量,并将其输入SSA-LSSVM模型中进行识别诊断。

综上所述,所提变压器内部机械故障诊断方法的流程图如图1所示。

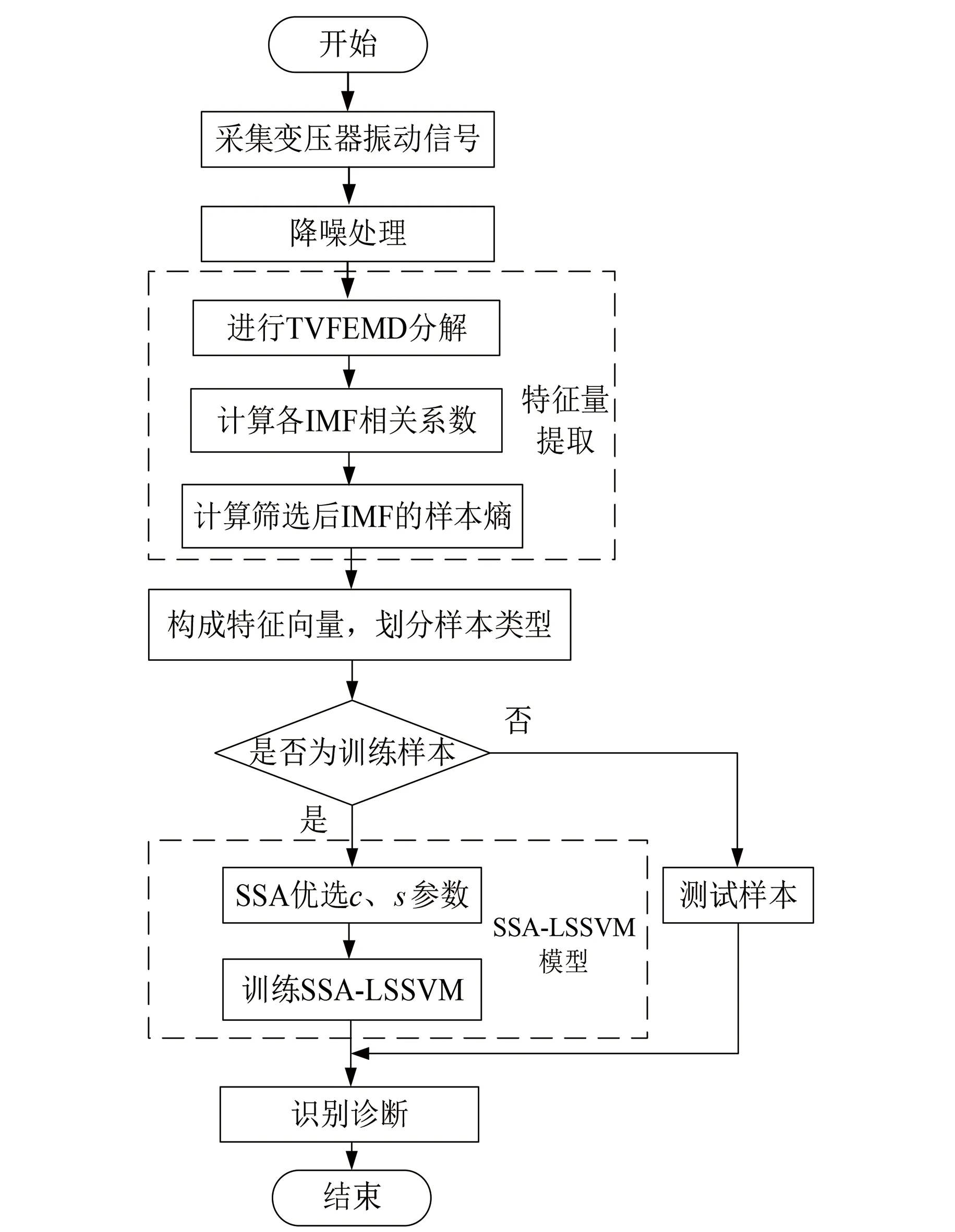
图1 故障诊断流程图

4 试验结果验证与分析

本文对一台10 kV变压器进行铁心松动故障模拟试验。具体地,通过改变变压器铁心松动程度来模拟变压器内部机械状态的变化,将采集到的振动信号用于后续的故障诊断过程中。试验时将三个振动传感器置于变压器油箱顶部,分别记为测点1、测点2和测点3,具体测点位置如图2所示。需要说明的是,传感器采用型号为1A212E的IEPE型压电式加速度传感器,采样频率为20 kHz。

图2 变压器测点布设图

在试验开始前,对变压器进行抽油、吊罩操作,通过改变铁心的压紧螺母预紧力来实现铁心松动故障过程的模拟。本试验主要模拟了正常状态、铁心松动25%状态和铁心松动50%状态这三种典型故障状态。整体试验原理示意图如图3所示。调压器输入380 V额定电压,变压器空载运行,振动传感器采集的数据经采集仪被计算机接收。其中,采集仪的型号为DH5922D。

以测点2位置的数据为例,本文测得的变压器三种不同状态的振动信号如图4所示。

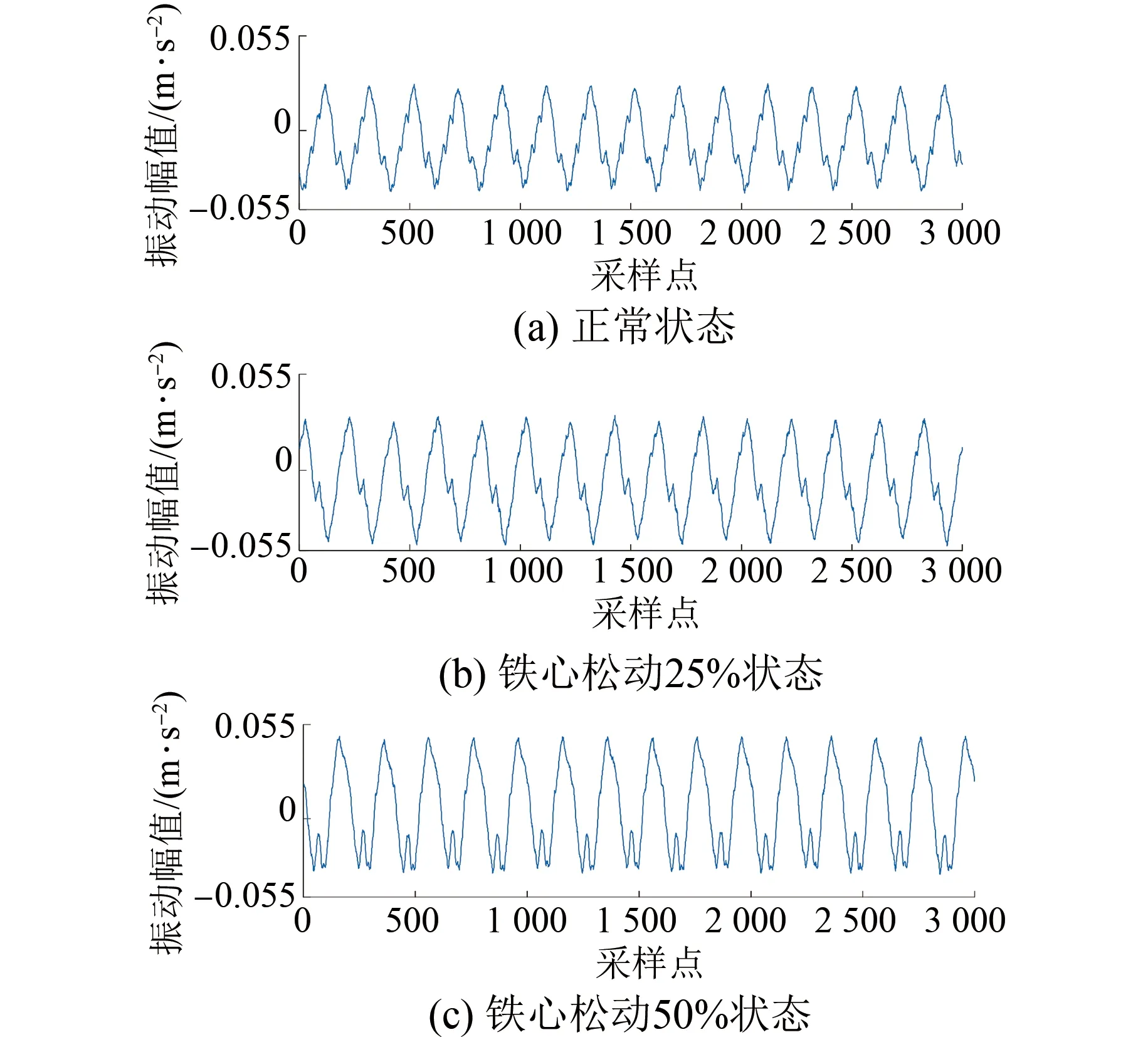
图4 变压器不同状态2号测点位置振动信号

本文进一步利用TVFEMD对上述三种变压器的振动信号分解,所得IMF分量如图5所示。需要说明的是,为了充分有效地提取振动信号特征信息,避免出现模态混叠和分解过剩的情况,本文选择模态分量个数为6。

图5 TVFEMD分解图

为避免特征冗余,采用相关系数法确定分解后所得6层IMF分量与原始信号的相关性。变压器三种状态下每个IMF分量的相关系数值如表1所示。值的注意的是,表1中的状态1、状态2和状态3分别表示正常状态、铁心松动25%状态和铁心松动50%状态。

表1 三种状态下每个IMF分量相关系数值

根据式(24)得到阈值标准为0.060 8,由表1可知,6层IMF分量中只有IMF2与IMF3符合标准,其余分量应在特征提取时被剔除。因此,计算各状态下IMF2与IMF3的样本熵,计算结果如表2所示。

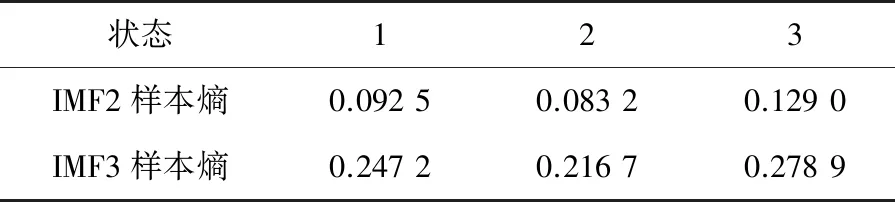
表2 IMF2与IMF3样本熵计算结果

由此,即构成一组特征向量,该特征向量由IMF2与IMF3的样本熵组成, 将其分别输入到LSSVM、PSO-LSSVM和SSA-LSSVM模型中进行分类识别。其中,训练样本为200组,测试样本为120组。各模型的测试分类准确率如图6所示,其中状态1、状态2和状态3分别表示正常状态、铁心松动25%状态和铁心松动50%状态。

图6 不同方法的分类结果

由图6可知,传统LSSVM模型与PSO-LSSVM模型在识别三类变压器铁心状态特征时均出现了识别错误的情况,而SSA-LSSVM模型仅出现了一次识别出错。这表明本文所提方法的分类识别效果更优。

为了进一步说明本文所提方法的优越性,计算了上述三种识别模型在识别变压器铁心松动故障时的单一诊断准确率和整体诊断准确率,其结果如图7所示。

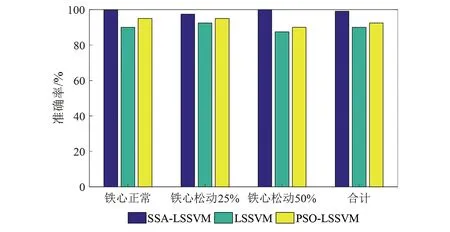
图7 三种识别模型诊断准确率的对比

由图7可知,文中所提基于TVFEMD和SSA-LSSVM的变压器内部机械故障诊断方法对各程度的铁心松动故障均有较高的诊断准确率,且所提算法的诊断准确率均高于其他算法。整体来看,基于SSA-LSSVM模型的诊断准确率达到99.17%,而其他两种对比模型的诊断准确率分别为90%和92.5%。这也表明SSA对LSSVM的参数优化效果更好,构建的故障诊断模型准确率更高,可为变压器检修策略的制定提供相应指导。