基于命令滤波反步法的双电机离散同步控制*

何建华, 宋润生, 蔡明洁,2, 王保防,2

(1.青岛大学 自动化学院,山东 青岛 266071;2.山东省工业控制技术重点实验室,山东 青岛 266071)

0 引 言

近年来,“智能制造2025”国家发展战略对伺服电机高速、高精度、高可靠性等指标提出了新的要求与挑战[1]。随着要求的不断提高,电机自身的参数和电机在驱动时不可避免的摩擦等扰动更易影响伺服电机的控制[2]。为了使电机能够高效平稳运行,滑模控制[3]、轨迹跟踪控制[4]、摩擦补偿控制[5]、鲁棒控制[6]、模糊自适应控制[7]等控制方法应运而生,在控制领域获得了高度认可。

目前,针对伺服电机高精度控制问题,文献[8]提出了鲁棒跟踪控制,该方法在反馈线性化的基础上降低不确定项对驱动系统的影响。文献[9]提出了一种自适应模糊控制,该方法不要求控制对象有具体的数学模型,当出现不确定因素时仍能保持较好的性能。文献[10]提出了一种有效时间控制方法,使系统收敛更快,减小了跟踪误差,该方法大规模应用于机器人、船舶、车辆等领域[11]。然而上述文献采用的方法大都应用于连续系统模型,但伺服电机在实际工程中绝大多数使用的是离散系统模型,该模型更具有现实应用价值[12]。受采样时间离散化的影响,电机的追踪性能和同步追踪精度可能会降低,因此离散伺服电机控制亟待研究。

随着研究的深入,文献[13]提出了事件触发指令滤波离散控制方法,系统的自适应律和控制律将由设定的触发条件来判断。文献[14]在命令滤波的基础上结合神经网络技术,对具有多输入约束的离散系统有较好的跟踪效果。文献[15]设计了动态面模糊离散速度调节器,降低计算难度的同时有效减轻控制器设计的复杂性。目前对于离散的研究多数针对单电机系统,单电机的功率相较于双电机有明显的差距[16],而现实工程中的大惯量负载多数采用双电机来操控[17]。目前双电机离散控制仍然有许多不足之处,例如电机之间不同的电机参数[18]导致的电机转速不同步、多电机带来的多轴摩擦动态[19]和转矩扰动[20]导致的电机过载问题等。因此实现双电机系统的离散高跟踪性能控制是一个巨大的挑战。

本文针对双电机同步驱动伺服系统进行离散化建模,在忽略齿隙的影响下建立双电机离散模型和动力学方程。设计基于双电机离散控制下的命令滤波反步法,设计补偿系统消除误差,减轻计算负担。利用神经网络技术逼近多电机轴转矩等非线性扰动函数,使得控制器在考虑非线性扰动的影响下仍具有良好的追踪性能。

1 双电机伺服系统建模

在双电机伺服系统中,两台电机通过减速器、小齿轮和大齿圈一起带动旋转负载,使得负载以相同的速度运行。忽略齿隙的影响,其离散模型如下:

(1)

式中:字母j为电机参数组(j=1,2);θj为电机的角位置;ωj为角速度;KTj为电磁转矩常数;Jmj为电机转动惯量;bL为电机负载侧摩擦因数;bj为电机的黏滞摩擦因数;uj为输入电流;KL为刚度系数;Fmj为系统的非线性扰动;Δt为采样周期。

双电机离散同步驱动系统控制策略框图如图1所示。由图1可知,在双电机伺服系统中,利用电机实际位置与给定的期望位置之间的差值得到误差信号,构建虚拟控制信号,并将虚拟控制信号输入到命令滤波器中得到输出信号。该输出信号一方面作为模糊反步控制器的输入,另一方面输入到误差补偿信号模块产生误差补偿信号输入到控制器中。

图1 双电机同步控制策略框图

双电机同步驱动伺服系统结构图如图2所示。选择变量如下:

图2 双电机同步驱动伺服系统结构图

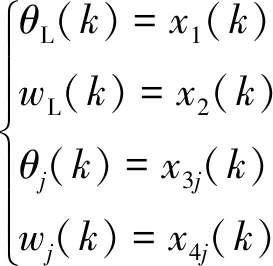
(2)

双电机离散模型表示为

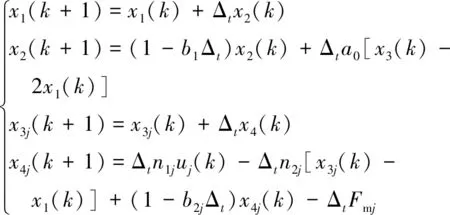
(3)

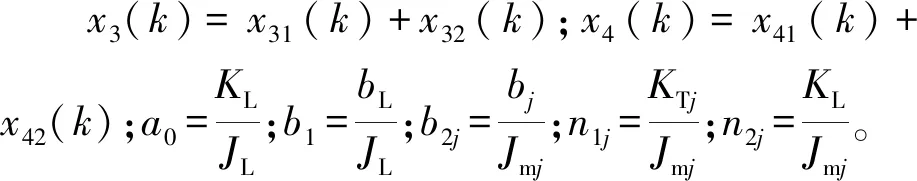
2 控制器设计

定义系统误差为

(4)

定义系统补偿信号可表示为

(5)

式中:xd为给定的期望信号;x2,c、x3,c、x4,c分别为x2、x3、x4滤波后的期望虚拟信号;x4j的期望虚拟控制信号设置为x4,c/2;另外用es表示两个电机的速度误差;ej(k)为系统误差;ζj(k)为补偿信号,j=1,2,3,4。

步骤一:由式(3)的第一个方程以及式(4)、式(5)得出:

v1(k+1)=e1(k+1)-ζ1(k+1)=

x1(k)+Δtx2(k)-xd(k+1)-ζ1(k+1)

(6)

(7)

分别构造虚拟控制律α1(k)和误差补偿ζ1(k)可得如下表达式:

(8)

ζ1(k+1)=Δt[ζ2(k)+x2,c(k)-α1(k)+

t1ζ1(k)]

(9)

式中:|t1|≤1。

结合式(8)、式(9)得:

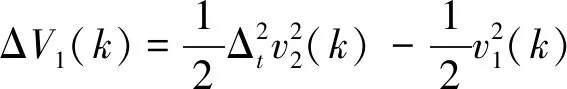
(10)

步骤二:由式(3)的第二个方程以及式(4)、式(5)得出:

v2(k+1)=e2(k+1)-ζ2(k+1)=

(1-b1Δt)x2(k)+Δta0[x3(k)-2x1(k)]-

x2,c(k+1)-ζ2(k+1)

(11)

2x1(k)]-x2,c(k+1)-ζ2(k+1)}2-

(12)

分别构造α2(k)、ζ2(k):

t2ζ2(k)

(13)

ζ2(k+1)=Δta0[ζ3(k)+x3,c(k)-α2(k)+

t2ζ2(k)]

(14)

式中:|t2|≤1。

由式(13)、式(14)得:

(15)

v3(k+1)=e3(k+1)-ζ3(k+1)=

x3(k)+Δt[x41(k)+x42(k)]-

x3,c(k+1)-ζ3(k+1)

(16)

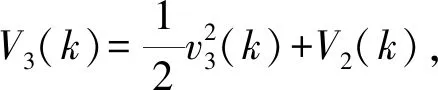
x3,c(k+1)-ζ3(k+1)}2-

(17)

分别构造α3(k)、ζ3(k):

(18)

ζ3(k+1)=Δt[ζ4(k)+x4,c(k)-α3(k)+

t3ζ3(k)]

(19)

式中:|t3|≤1。由式(18)、式(19)得:

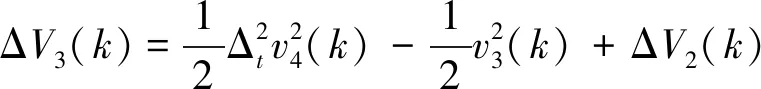
(20)

步骤四:由式(3)的第四个方程以及式(4)、式(5)可得:

v4(k+1)=e4(k+1)-ζ4(k+1)=

(21)

(22)

其中,令f3(k)=Δtn21[x31(k)-x1(k)]-(1-b21Δt)x41(k),f4(k)=Δtn22[x32(k)-x1(k)]-(1-b22Δt)x42(k)。

由于式(22)中含有非线性扰动,定义一个新函数

(23)

(24)

式中:ΔtFmj为系统设定的非线性扰动函数;Z2j(k)=[x1(k),x2(k),x3(k),x4(k),x5(k),x6(k)]T;τ2j为逼近误差,并满足不等式|τ2j|≤ε2j;‖W2j‖为向量W2j的范数。

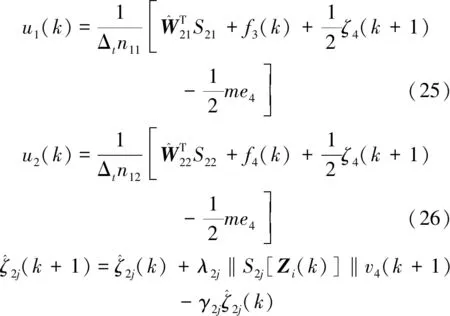
(27)

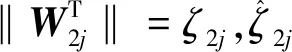
(28)

3 稳定性分析

考虑同步误差的情况下,选取Lyapunov函数:

(29)

求取V(k)的一阶差分,可得:

(30)

在Lyapunov函数中考虑速度同步误差,在保证跟踪性能的同时能提高电机间的同步度。

神经网络权值自适应律:

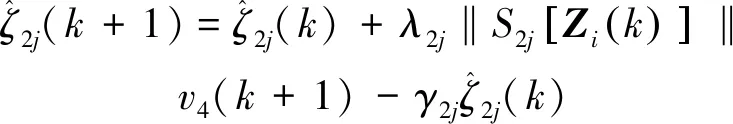
(31)

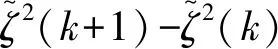
(-λ2j)2ζ2j(k+1)‖S2j[Zi(k)]‖v4(k+1)+

(32)

神经网络基函数满足‖S2j[Zi(k)]‖2≤li,根据杨不等式可得:

(33)

由离散模型式(3)以及式(4)得出:

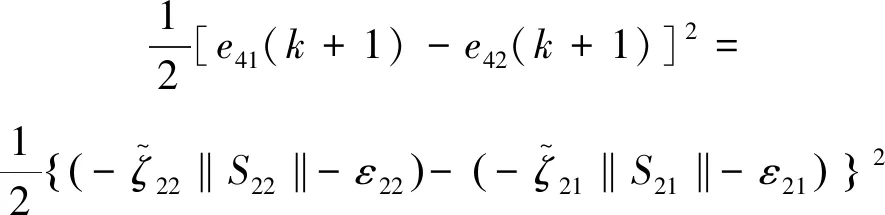
(34)

将式(33)代入式(30),其中:

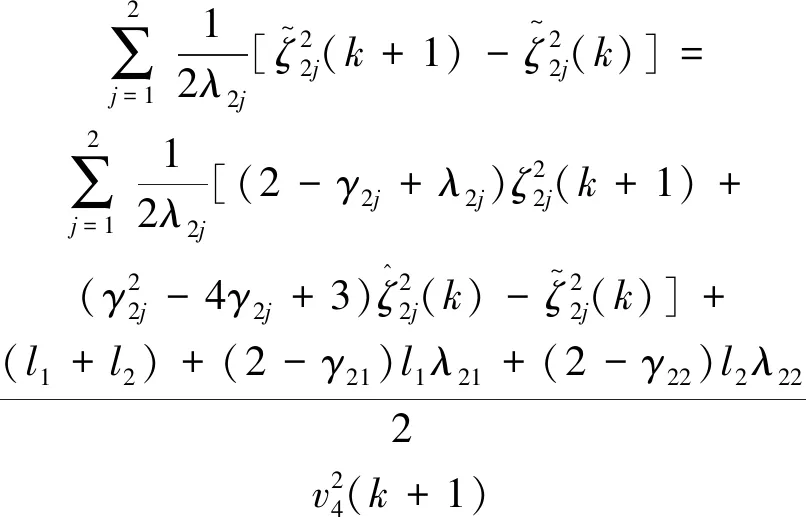
(35)

取ζ4(k)=0,由于v4(k)=e4(k)-ζ4(k),可得v4(k)=e4(k),将式(34)、式(35)代入式(30),由杨不等式得:

ΔV(k)≤[3(l1+l2)+3(2-γ21)l1λ21+

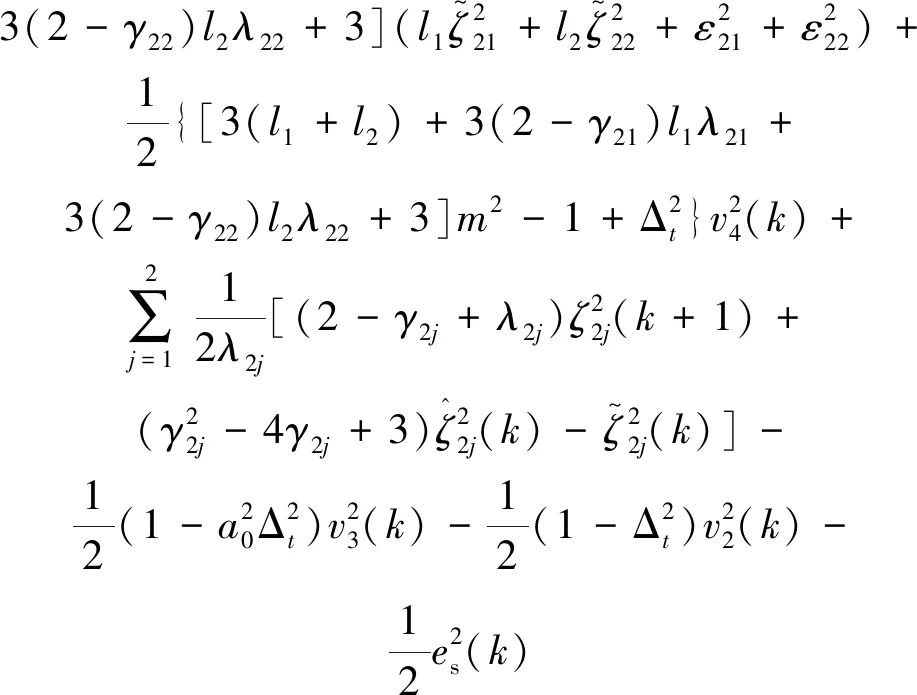
(36)

4 仿真分析

为了验证该离散同步控制方法的可行性,在MATLAB环境中进行仿真分析。选取采样周期Δt=0.002 5 s,采样次数为12 000。

电机的参数如下:Jm1=0.4 kg·m2;Ke1=0.76 V/rad,Ke2=0.1 V/rad;KT1=1.1 N·m/A,KT2=0.9 N·m/A;R1=2.5 Ω,R2=3 Ω;L1=0.05 H,L2=0.04 H;b1=b2=0.001 158 N·m·s/rad。

负载为JL=2(Jm1+Jm2)=2.4 kg/m2,同时KL=50 N·m/rad,bL=0.03 N·m·s/rad。控制器参数和滤波器参数选择为ks=10,kc=10;w1=30,w2=0.08。

期望信号选为yd(k)=cos[t(k-1)π/2]。选择相同的参数,比较命令滤波反步法(CFC)和动态面控制方法(DSC),从而验证CFC方法的优越性。仿真结果如图2～图6所示。

图3(a)和(b)分别为DSC和CFC控制方法下的位置跟踪曲线,图4为DSC和CFC控制方法下的追踪误差信号,图5(a)和(b)分别为DSC和CFC控制方法下的电机输入信号,图6(a)和(b)分别为DSC和CFC控制方法下的电机转速,图7为DSC和CFC控制方法下的同步误差信号。

图3 位置跟踪曲线

图4 追踪误差信号

图5 电机输入信号

图6 电机转速

图7 同步误差信号

将DSC方法和CFC方法进行对比,根据图3可以看出CFC方法具有更好的追踪效果。图4分别显示了两种控制方法下的追踪误差,相较于DSC方法,本文采用的CFC方法误差更小,可以保持在-0.13～0.13 rad以内,跟踪性能较好。图5分别显示两种控制方法下的电机输入电压,DSC方法下的电机输入电压波动较大;CFC方法下两个电机之间的电压更加稳定,波动较小,电机运行更加平稳。图6显示了DSC方法和CFC方法下的两个电机的转速,对比之下不难发现CFC方法下的两个电机速度更为接近,波动更小,运行更平稳。图7可以看出CFC方法下电机之间转速误差保持在-0.08～0.08 rad之间,且同步性能良好。根据仿真结果得出所设计的控制器具有较好的追踪效果,误差收敛到非常小的邻域内,表现出很好的跟踪性能与同步性能。

为了验证突加负载扰动时双电机系统在所提控制方法下的抗扰性能,在仿真第15 s时突加10 N·m的转矩。图8为负载扰动下的位置跟踪误差,图9为负载扰动下的电机转速,图10负载扰动下的同步误差信号。

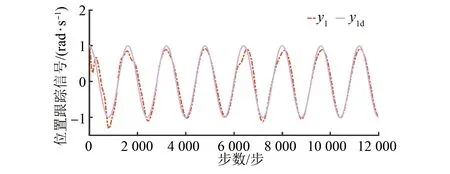
图8 负载扰动下位置跟踪信号

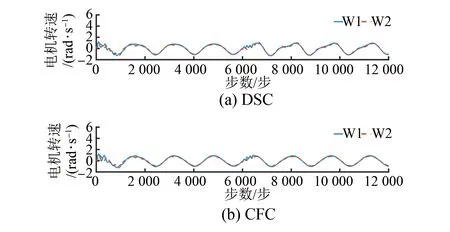
图9 负载扰动下电机转速

图10 负载扰动下同步误差信号

由图8可以看出,在突加负载扰动后,电机的位置跟踪曲线出现波动,相较于突加扰动前误差增加了0.12 rad;图9显示了突加负载扰动后电机转速,相较于突加扰动前,电机转速下降0.04 rad/s;图10为突加扰动后的同步误差信号,扰动后电机的同步误差增加了0.05 rad/s,仍能保持较好的同步性能。

5 结 语

本文研究了双电机离散模型下的同步控制方法,设计的控制器能够有效地减少两个电机在离散状态下的追踪误差和同步误差,使得两个电机在相对平稳的状态下运行。该控制器使用命令滤波技术,结合神经网络技术逼近多电机轴转矩等非线性扰动函数在反步法的基础上减轻了计算负担。二阶滤波器消除了滤波误差带来的不良影响,使得误差控制在合理的区间范围,在保证控制性能的同时仍具有较高的控制精度。此仿真结果验证了上述方法的可行性。