基于ALE算法的高速水射流对船体表面冲击特性研究

熊 庭,康 丁,方珍龙

(1.武汉理工大学 交通与物流工程学院,武汉 430063;2.武汉理工大学 三亚科教创新园,三亚 572025;3.武汉理工大学 国家水运安全工程技术研究中心,武汉 430063;4.武汉理工大学 船海与能源动力工程学院,武汉 430063)

近年来,我国大力推进海洋强国战略,海洋经济在社会经济发展比重逐年上升。海洋生物会吸附在船舶表面,导致其表面粗糙度和航行阻力增大、航行成本及碳排放增加[1],同时海生物黏液会对金属造成腐蚀,影响安全性[2],需定期进行清洗。非接触式清洗如合适水压保护涂层的高压水射流清洗法[3]近几年得到更多研究。高压水射流清洗作为船舶表面清洗新技术,通过射流的冲击动能清除表面污染物,其具有效率高、清洁环保等优点[4]。但高压水射流清洗附着物同时也对附着物基体钢板进行持续性冲击,钢板内部应力变化可能会对钢板材料脆性、抗拉强度等性能造成影响[5]。因此研究高压水射流对附着物基体钢板的影响将对优化水射流清洗船体附着物技术具有重要意义。

目前国内外学者进行了大量的理论研究、试验测试和数值模拟来了解水射流对靶件(工件)材料的破坏作用过程及其机理。周正[6]基于磨料水射流的材料冲蚀去除机理分析了磨料粒子作用力,结合流体冲蚀仿真和单因素试验验证了磨料水射流抛光钛合金的可行性。葛兆龙等[7]开展了水射流破岩试验,采用扫描电镜和核磁共振技术分析了煤岩的破坏形式、微观形貌和孔隙结构的变化。程书铭等[8]使用200 MPa的超高压水对船用A级钢进行射流冲蚀试验建立了水射流冲蚀剥离模型,阐明了水射流冲蚀作用机理。胡东等[9]利用自制喷嘴形成脉冲气液射流冲蚀混凝土件,与自振脉冲水射流比较进气方式对冲蚀效果的影响规律。刘佳亮等[10]对射流冲击混凝土进行了试验研究,其结果表明混凝土破碎区演进过程分为水锤压缩区和非压缩区扩展以及侵彻贯通后扩展三个阶段。Lu等[11]进行了纯水射流冲击岩石试验,认为水射流冲击按时间顺序主要分为水锤压力和滞止压力阶段。Srivastava等[12]研究了脉冲射流加工处理不锈钢工艺效果,并根据残余应力和强化效应来评价脉动水射流性能。

随着计算机技术的发展,数值模拟逐渐被应用于模拟高速水射流冲击固体靶板的过程。Hsu等[13]釆用欧拉-拉格朗日耦合法建立了水射流冲击固体表面的三维有限元模型,研究了工件结构变形和冲击表面压力特征。Gong等[14]使用ALE(arbitrary Lagrange-Euler)算法进行模拟,得出磨粒直径等参数与切削深度之间的关系。黄璐云等[15]利用计算流体动力学(computational fluid dynamics,CFD)模拟可压缩性空化水射流,对超高压水射流除锈喷嘴进行了三维仿真计算。司鹄等[16]利用平滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法建立了脉冲射流破岩的数值计算模型,对脉冲射流在破岩过程中应力波的产生、传播及衰减过程进行了模拟。潘越等[17]基于SPH-FEM耦合算法,建立了截断式脉冲水射流冲蚀煤岩的数值模型,分析了围压、脉冲长度及流速等因素对其冲蚀深度和速度的影响规律及破坏机理。Ren等[18]以SPH-FEM 耦合算法来构建水射流冲击模型,分析岩石在受到水射流强力冲击时的损伤表现,结果显示岩石破坏形式表现为剪切裂纹和拉伸裂纹两个部分。

综上所述,目前国内外对高压水射流冲击损伤的研究对象主要是高压水射流冲击岩样和磨料水射流冲蚀金属,而高压水射流对附着物基体钢板的应力损伤研究较少。近年来利用数值模拟技术使用简化模型对复杂运动变化规律进行研究的手段得到大量应用。基于拉格朗日网格的有限单元法在处理大变形时容易出现网格畸变从而降低计算精度[19],而任意拉格朗日-欧拉方法(ALE)将欧拉网格和拉格朗日网格耦合起来,有效解决了大变形计算精度低的缺点[20]。因此本文从流固耦合理论出发,基于任意拉格朗日-欧拉流固耦合算法(ALE)建立了水射流冲击船体表面的有限元模型,模拟了不同入射速度v和入射角θ条件下的水射流冲击钢板过程,分析了高压水射流冲击压力特征以及应力影响,为水射流清洗船体附着物过程中对船体基体损伤和水射流清洗参数的选取提供理论依据。

1 数值模拟

1.1 基本原理

1.1.1 控制方程

基于ALE算法的控制方程可表示为[21]

(1)

(2)

(3)

(4)

式(1)为质量守恒方程,式(2)为动量守恒方程,式(3)和(4)为能量守恒方程。其中:ρ为物质密度;fi为单位质量的体力;σij为柯西应力张量;e为单位质量的内能;qi为热通量;下标i=1,2,3,j=1,2,3分别为坐标轴的方向;wi为相对速度,wi=u-v,u为物质的运动速度,v为空间网格运动速度。

1.1.2 数值方法

ALE计算过程的核心算法是对流算法,它是控制新网格与旧网格之间物质传递的一种映射关系。当网格单元达到一定的变形量后需要通过一定的光滑算法进行自我重新构置网格,能量、应力等传递在新旧网格单元之间进行。本文采用半指数漂移算法(half index shift algorithm)和共体细胞算法(donor cell algorithm)[22],假设对流算法中需要传递的物质名称为f,则可以通过共体细胞算法来计算需要运输的量值

(5)

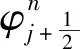
(6)

式中:Δt为时间步长;Δx为单元特征长度。式(6)与式(7)是针对ALE算法中的一维对流情况,如果要求解三维对流量,则需要采用一阶精度的半指数漂移算法[23]

(7)

(8)

式中:a,b,c与d为矩阵常数;f为需要运输的物质名称;φ为某节点的初始量;j为节点数。

1.2 计算模型

1.2.1 水与空气模型

水与空气设定为完全塑性材料。采用NULL本构模型来模拟流体介质。采用POLYNOMIAL状态方程提供空气介质压力P,如式(9)

(9)

式中:E为空气的初始单位体积内的内能;μ为空气的比体积,μ=ρ/ρ0-1,其中ρ/ρ0为压缩(膨胀)后与压缩(膨胀)前的空气密度之比。假设空气为理想空气,因此常数项C0=C1=C2=C3=C6=0,常数项C4=C5=γ-1,其中γ表示为

γ=CP/CV

(10)

式中,CP和CV分别为空气定压比热容和定容比热容。因此本文中的空气状态方程可表示为

(11)

本文采用GRUNEISEN状态方程来提供水介质压力P,可表示为

(12)

式中:Cs为冲击波速度;S1,S2和S3为us-uP关系曲线的斜率系数;γ0为Mie-Gruneisen常数;a为对γ0的一阶体积修正系数;E为初始单位体积的内能。空气和水的密度分别为1.293×10-3g/cm3和1 g/cm3,方程系数数值如表1所示。

表1 状态方程系数Tab.1 State equation coefficients

1.2.2 钢板模型

本文忽略水射流冲击过程中靶板的形变,因此采用普通钢材作为试验靶板,钢材材料属性如表2所示。采用PLASTICITY材料作为钢制靶板的本构模型。

表2 钢板材料参数Tab.2 Material parameters of steel plate

1.2.3 网格划分与求解设置

图1为水射流冲击靶件1/2简化模型。水射流简化为一根直径Φ=2 mm,长度L=2 mm的均匀水柱。由于水射流直径只有2 mm,与船鼻艏、螺旋桨这些大尺度弯曲件相比,水射流冲击的部位相对于水射流可近似看成规则的平面。靶件长l=10 mm,宽d=5 mm,高h=5 mm。整个模型分为A、B、C三个域,A为射流源;B为空气域;C为靶件域。水射流冲击方向与靶件表面法线的夹角为入射角θ。A、B域由ALE网格划分网格。C域由拉格朗日网格划分。

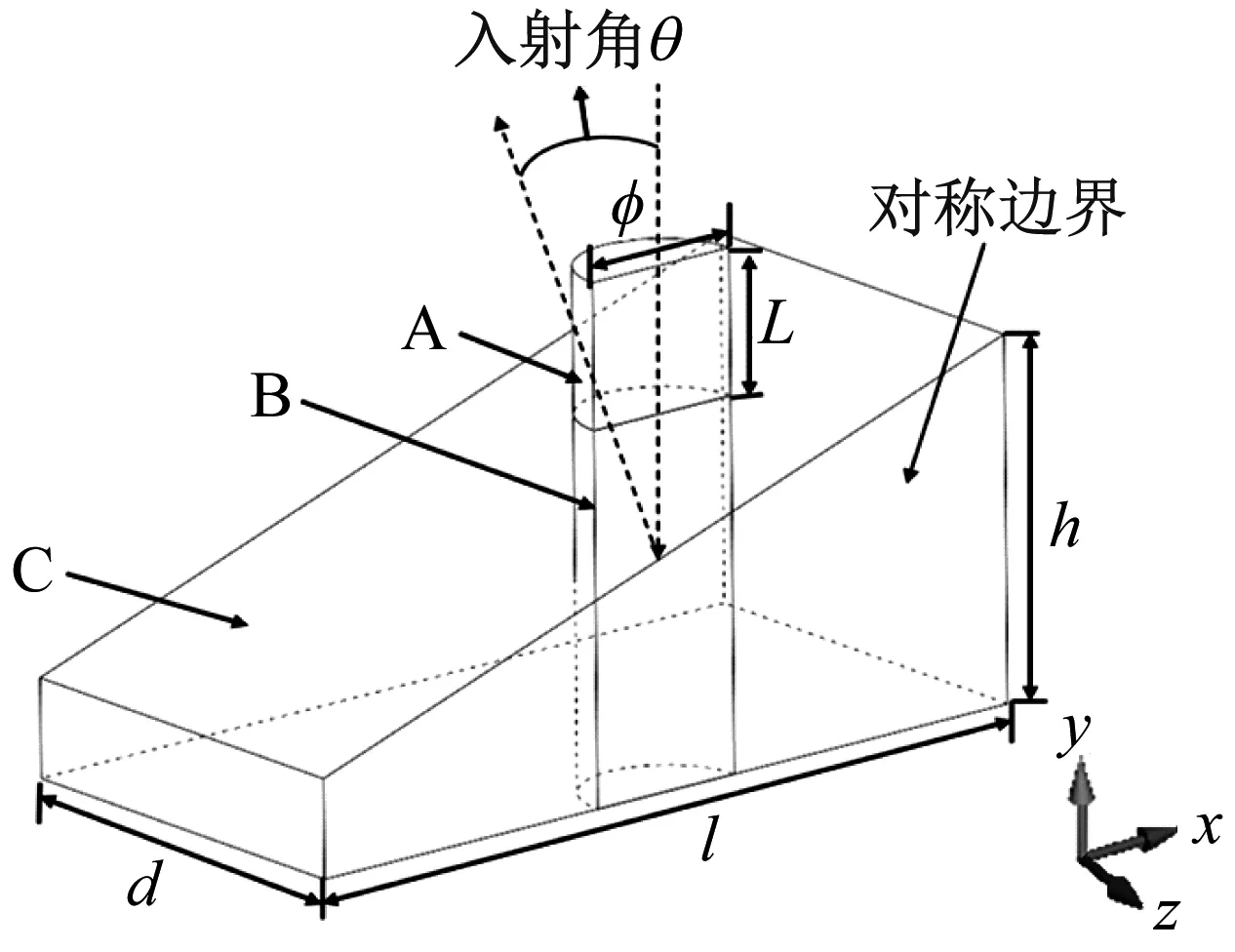
图1 水射流冲击数学模型Fig.1 Mathematical model of water jet impact

射流对工件的影响是通过耦合ALE和Lagrange的网格来实现的,因此在该模拟中B和C网格需要重叠,如图2所示。应力变化集中在射流和工件的接触区域附近,因此需要在C的中心区域进行网格加密。B与C通过LS-DYNA中的关键字*CONSTRAINED-LAGRANGE-IN-SOLID实现结构与流体的耦合。靶件域C的底部为固定位移边界,除对称边界外其余三个面采用无反射边界,以模拟无限边界,减少初始材料网格域。XOY面为对称边界。

(a) θ=0°

1.2.4 网格无关性验证

本文分别进行入射角θ=0°、10°、15°、20°条件下网格无关性验证,选择了不同入射角θ下对应的最佳网格数量,由于篇幅限制,在入射角θ=0°时水射流速度为375 m/s的工况条件进行网格收敛性验证。以冲击后靶件中心稳定压力为对比结果,逐步加密网格,结果如图3所示。当模型网格数大于230万,计算结果变化很小,可认为此时计算结果与网格疏密相关性很小。因此,本文模型入射角θ=0°时网格数目取230万。

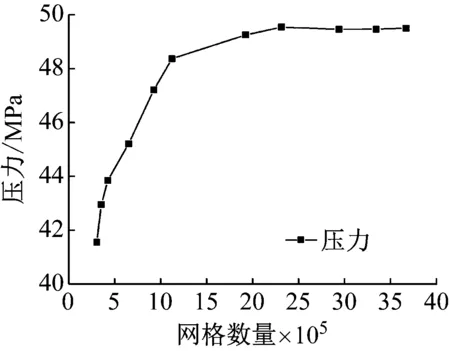
图3 不同网格数目下靶件中心稳态压力变化图Fig.3 Variation of steady-state pressure at the center of the target under different grid number

1.2.5 模拟验证

为验证LS-DYNA高压水射流冲击有限元仿真在五种不同流速下的模拟准确性,因此使用相同尺寸水射流模型与采用ABAQUS软件进行模拟计算的Hsu等得出的模拟数据进行比较,如图4所示。由图4可知,模拟结果与Hsu等模拟结果吻合度较高,因此该求解策略可较为准确的模拟在不同流速下的高压水射流冲击。

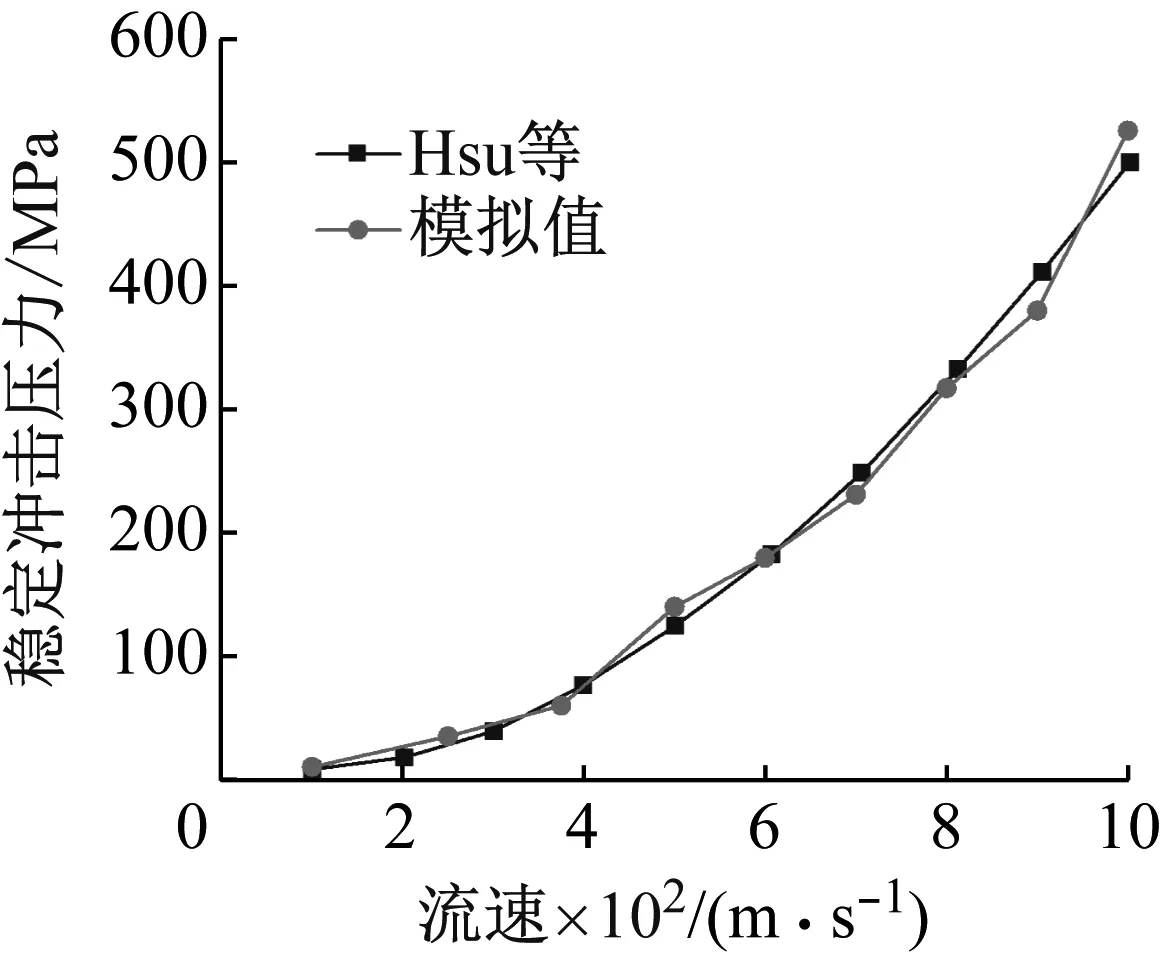
图4 不同流速下流动稳态冲击压力模拟值与Hsu等模拟值比较Fig.4 Comparison of simulated and Hsu etc simulation values of flow steady-state shock pressure at different flow rates

2 数值计算结果分析

为了模拟不同流动状态下的水射流,选取100 m/s,250 m/s,375 m/s,500 m/s,600 m/s五种速度作为水射流速度,在该速度范围内水射流从亚音速到超音速状态,模拟结果更全面。

2.1 不同入射角θ冲击钢板的压力特征

图5为入射角θ=0°,10°,15°,20°下水射流以不同速度冲击下靶件中心的压力随时间变化曲线,线1～5分别代表射流流速v为100 m/s,250 m/s,375 m/s,500 m/s,600 m/s。

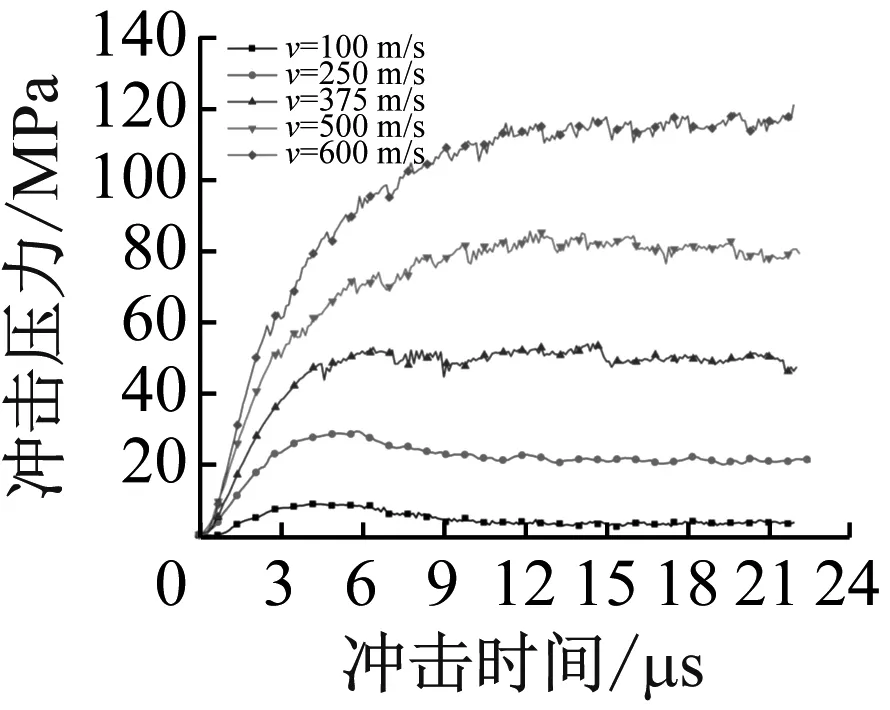
(a) θ=0°

如图5(a)所示,当水射流速度小于300 m/s时,水射流冲击到靶体瞬间,冲击压力逐渐升高达到压力峰值后逐渐降低至某一稳定值,随后冲击压力在这一稳定值上下波动,该稳定值与峰值压力差距较小。图5(b)与图5(a)相比,当射流速度小于300 m/s时,冲击压力曲线呈现出明显的水锤压力与滞止压力阶段:当水射流冲击到靶体的瞬间,冲击压力急剧升高,达到压力峰值后迅速降低至某一稳定值上下波动。由图5(c)可以看出,射流速度为375 m/s时滞止压力大小明显小于入射角θ=10°时射流速度为375 m/s所达到的稳定值大小,当速度为500 m/s和600 m/s时稳定值与入射角θ呈现正相关。图5(d)中100～600 m/s的冲击压力曲线都呈现出水锤压力与滞止压力阶段。滞止压力值随着水射流速度增大而增大,同时小于其他入射角θ下的稳定值。

可以得出,与垂直冲击靶件相比,以一定入射角θ冲击靶件会出现水锤压力与滞止压力阶段,同时随着入射角θ和水射流速度v增大,这种特征更明显。同时在相同速度条件下,当没有出现水锤压力与滞止压力阶段特征时,稳定值大小随着入射角增大而增大,而出现水锤压力与滞止压力阶段特征时,滞止压力值总是小于特定值。

2.2 入射角θ对峰值压力的影响规律

根据2.1节可以得出,不同入射角θ下靶体所受峰值压力的大小存在较大差异。入射角θ=0°、10°、15°、20°时靶件中心所受峰值冲击压力随射流速度的变化规律,如图6所示。

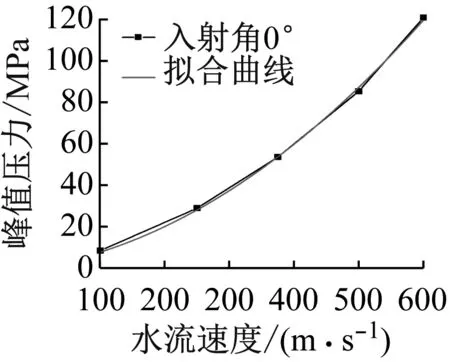
(a) θ=0°

采用数据拟合方法对数值结果进行处理,得到峰值压力大小P与射流速度v呈二次方关系

Pmax=av2+bv

(13)

式中:Pmax为峰值压力;v为水射流速度;a,b为拟合常数。在式(13)中,av2项表征动能大小,而bv项表征动量大小。通过式(13)可以看出,水射流以不同入射角θ冲击靶体时,其压力峰值均可表示为动能表征量与动量表征量之和[24]。

不同入射角θ下峰值压力回归分析系数a和b的大小变化如表3所示。不同角度下拟合系数R2均接近1,因此拟合优度高。由表3可以看出a在0°～15°时逐渐增大,而在入射角θ=20°时a值迅速降低至比垂直冲击时还小。而b随着入射角增大逐渐增大。

表3 不同入射角θ下峰值压力回归分析系数Tab.3 Regression analysis coefficients of peak pressure under different incident angles θ

由式(13)可知,a为高压水射流动能大小,而b为高压水射流动量大小。“动量”反映出使给定的物体得到一定速度需要多大的力,作用多长的时间。“动能”反映出使给定的物体得到一定速度需要在多大的力的作用下,沿着力的方向移动多长的距离[25]。由此看出适当的入射角冲击靶件能增加高压水射流动能,使冲击效果增强,而过大的入射角反而会降低水射流冲击动能,减弱冲击效果。而由于水射流动量大小随着入射角增大而增大,在水射流冲击方向上动量增大可以在极短时间内提供很大的力或者维持很大的力很长时间,因此增大入射角θ可以增大高压水射流的冲击影响范围。

2.3 钢板应力场模拟结果分析

2.3.1 靶体应力随冲击时间变化分析

水射流速度为375 m/s条件下入射角分别为0°和20°下冲击靶件时靶件表面和内部应力状态图,如图7所示。

(a) θ=0°

垂直冲击条件下靶体表面和内部应力分布较规律,如图8所示。靶体表面应力以水射流冲击点为中心呈现环形分布,图8(a)显示2 μs的状态,此时水射流开始冲击,加载时间较短,靶体中未形成足够的冲击载荷,因此靶体中产生的径向应力较小。高压首先出现在冲击区的边缘区域,然后扩散到周围区域,这可能是由于该水射流模型为平头圆柱形,冲击边缘区域相较冲击中心水流流动状态更复杂,因此应力变化更大。图8(c)显示在大约5 μs处,这种高强度应力以波浪的形式传播到周围区域。下一个时期,如图8(e)和图8(f)所示,随着冲击时间增大水射流达到稳定冲击靶件状态,同时射流沿靶体表面产生较大的径向流动,径向流动在靶体表面产生剪切效应。在拉应力和剪应力的共同作用下靶件表面应力大小提高且在冲击区域内应力大小中心低边缘高。

(a) θ=0°,t=2 μs

而以一定入射角θ冲击靶体时的应力场比垂直冲击时靶体应力场更复杂。图8(b)显示由于水射流模型为平头圆柱形,靶体表面在与水射流在首先接触区域出现应力集中,随着时间增大应力以该区域为起点扩散至冲击区域。图8对比θ=0°和θ=20°表面应力图片可看出以一定入射角θ冲击时,此时靶体表面同时受到水射流冲击产生的压应力和射流径向流动产生的剪应力的共同作用,由于存在入射角剪切效应更强从而靶体表面应力大小以及影响范围比垂直冲击时更大,同时靶体表面与水射流在首先接触区域应力更高,不像垂直冲击时应力分布呈现环形规律。

如图9所示,靶体内部的应力分布具有明显的局部性效应,沿射流中心向外传播,随着高压水射流的持续时间不断增大,靶体所承受的应力不断增大,应力影响范围不断扩大。值得注意的是图9(a)和(c)表明在水射流未达到稳定冲击状态时靶体内部会出现应力集中的现象,而随着时间增长水射流稳定冲击靶体内部应力增大且从上到下呈现先增大后减小的规律。以θ=20°冲击靶件时靶体内部应力从与水射流在首先接触区域扩散至周围区域,同时应力分布出现以冲击区域从上到下先增大后减小的分布规律。图9(d)和(f)显示θ=20°时5 μs和8 μs的状态,此时还未达到水射流稳定冲击状态,与图9(c)和(e)相比可知水射流未稳定时期以一定入射角θ冲击时靶体内部应力相比垂直冲击时增大,而图9(h)15 μs状态显示当水射流稳定冲击时以一定入射角θ冲击时靶体内部在水射流首先接触靶体区域附近出现应力集中,这与图9(g)展现的垂直冲击时水射流稳定冲击时靶体内部应力分布情况以yoz面对称分布不同,说明有一定入射角θ时,由于水射流流动状态相比垂直冲击时更复杂,靶体内部应力分布不规则。

(a) θ=0°,t=2 μs

2.3.2 稳定冲击时靶体内部有效应力分析

图10为四种不同入射角θ下水射流以不同速度冲击达到稳定冲击状态时靶体不同深度的有效应力变化趋势。由图10(a)～(c)所示,当入射角θ由0°增大到15°时,靶体表面有效应力在水射流速度大于等于375 m/s时随着入射角θ增大而增大,而入射角θ为20°时,靶体表面有效应力下降。这与2.2节得出的适当增加入射角θ提高冲击动能而过大入射角降低水射流冲击动能的规律相一致。观察到不同入射角下当速度小于等于375 m/s时,靶体内部有效应力大小分布相对均匀,没有明显应力集中现象。同时可看出不同入射角θ下靶体内部有效应力峰值出现在靶体深度1 mm左右,而θ=0°、10°、20°有效应力峰值更突出,意味着应力集中现象更明显,对靶体疲劳寿命影响较大。而入射角θ=15°时,靶体内部应力变化较为平缓,对靶体材料影响较小。

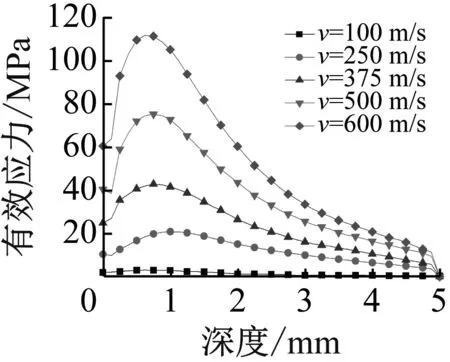
(a) θ=0°

将不同入射角下不同射流冲击下的靶体内部最大主应力进行比较,结果如图11所示,可以看出当速度小于375 m/s时,不同入射角下靶体内相似,当速度大于375 m/s时,在0°～15°内最大主应力随着入射角θ增大而增大,而入射角为20°时最大主应力随射流速度变化规律与入射角为0°时吻合度很高。

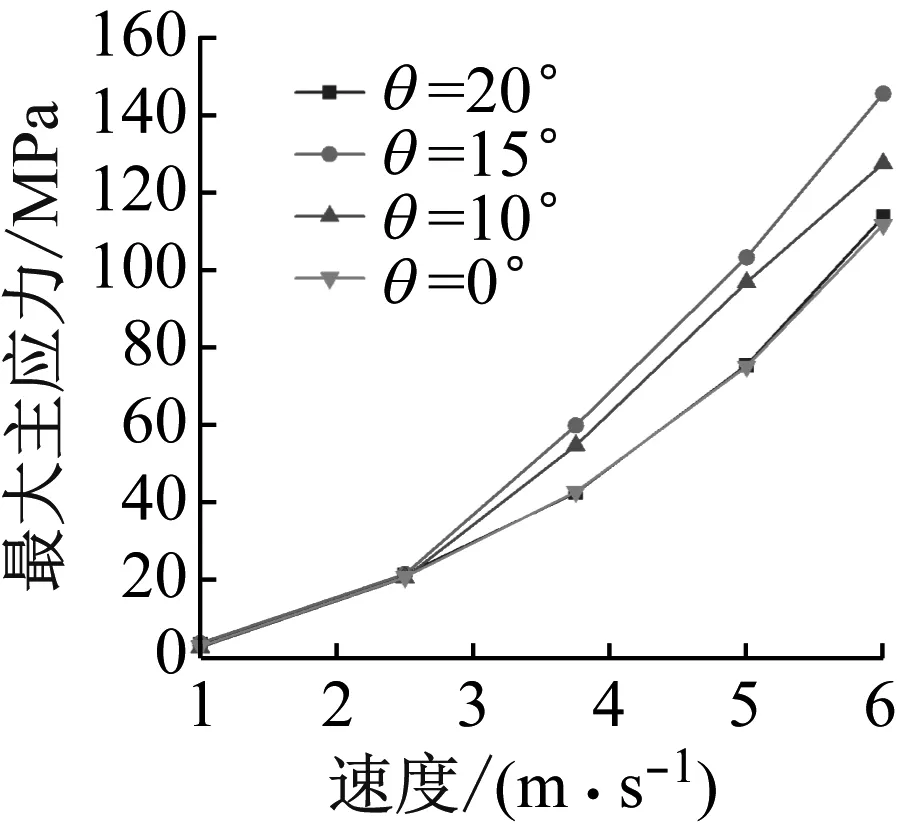
图11 稳定冲击时不同入射角θ冲击下靶体内部最大主应力应力随射流速度变化Fig.11 Variation of maximum principal stress inside the target with jet velocity under different incident angles θ during stable impact

为了更好地展现稳定冲击时射流速度v和入射角θ对靶体内部最大主应力影响的数量关系,绘制了以射流速度v和入射角θ为自变量,最大主应力为因变量的3D拟合曲面如图12所示。拟合公式形式如下

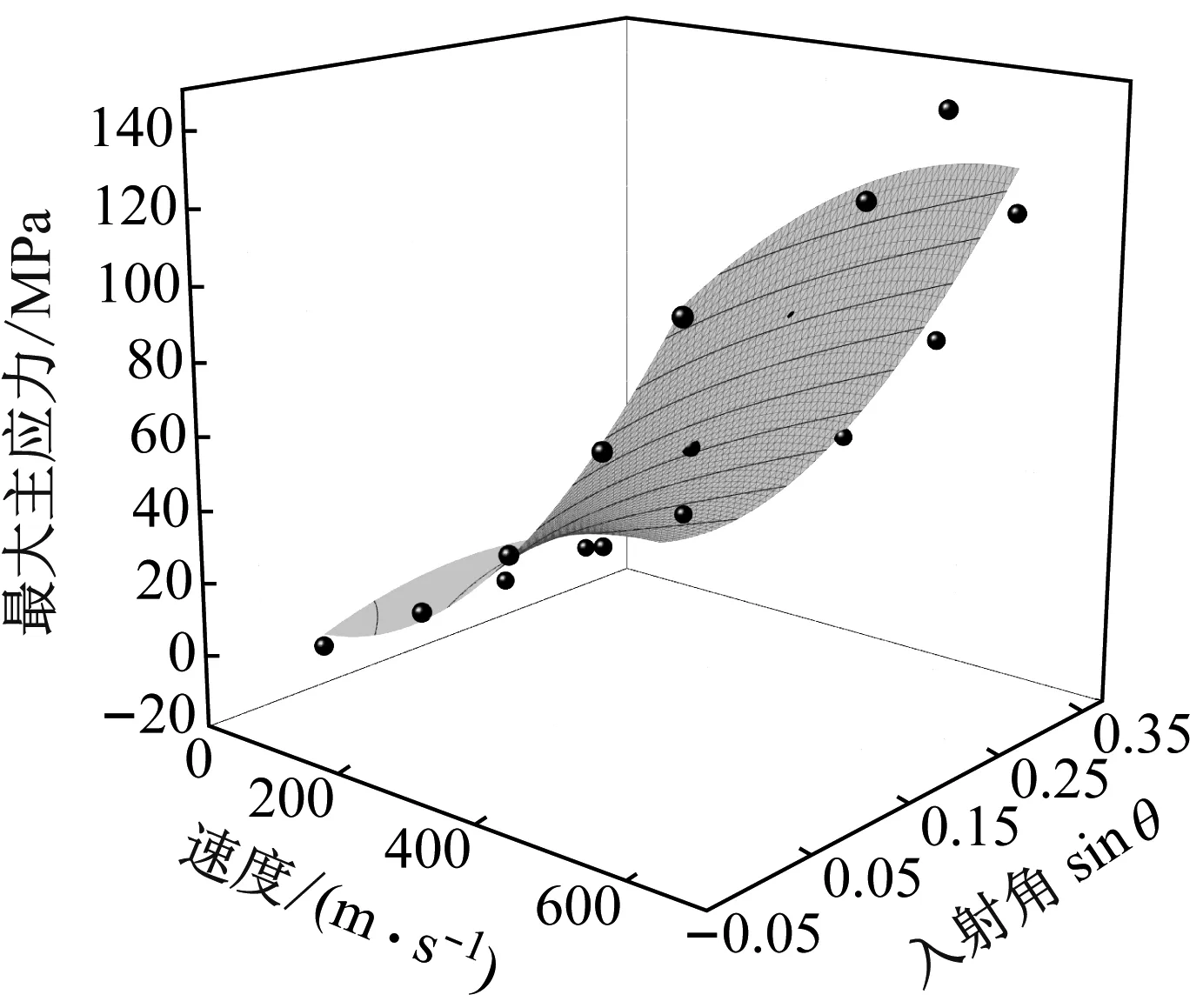
图12 稳定冲击时靶体内部最大主应力随着射流速度v和入射角θ变化关系Fig.12 The relationship between the maximum principal stress inside the target body as a function of the jet velocity v and the incident angle θ during stable impact

σ=Z0+Av+Bsinθ+Cv2+αsin2θ+βvsinθ

(14)

式中,σ为最大主应力。该公式拟合系数为0.970,接近于1,因此拟合优度高。拟合公式中拟合常数,如表4所示。

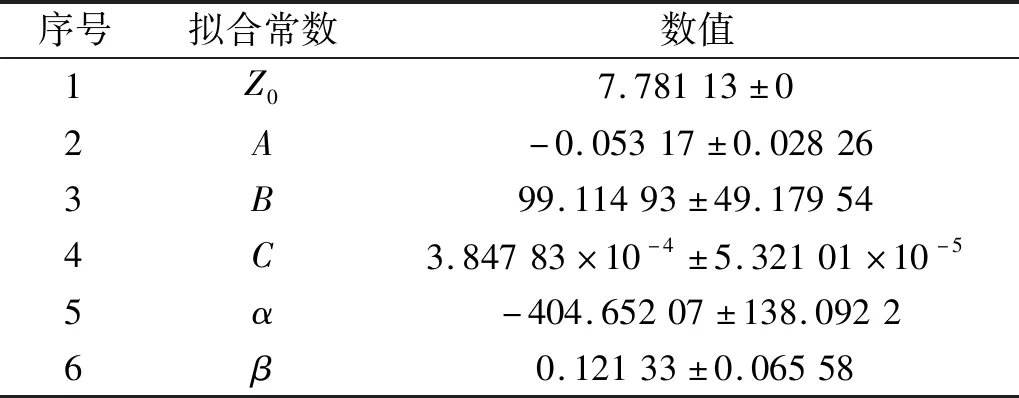
表4 最大主应力随着射流速度v和入射角θ变化拟合公式常数Tab.4 The maximum principal stress varies with the jet velocity v and the incident angle θ fitting formula constants

其中最大主应力关于射流速度射流速度v和入射角θ的导数为

(14)

(15)

(16)

3 结 论

以水射流冲击钢板为研究对象,利用有限元仿真方法进行了数值模拟研究,在0°,10°,15°,20°四个不同入射角θ下对v为100 m/s,250 m/s,375 m/s,500 m/s,600 m/s的五种不同流速进行数值模拟。与一般垂直冲击靶体情况不同,以一定入射角θ冲击靶体由于水流与壁面碰撞情况更复杂。主要结论如下:

(1) 随着入射角增大,靶件所受冲击压力会出现水锤压力与滞止压力阶段。随着水射流速度增大,稳定冲击状态下靶体所受冲击压力也随之增大。入射角θ=20°时水锤压力与滞止压力阶段特征最明显。

(2) 以适当的入射角θ冲击靶件能增加高压水射流动能,使冲击效果增强,而过大的入射角(θ=20°)反而会降低水射流冲击动能,减弱冲击效果。

(3) 以一定入射角θ冲击时由于剪切效应加强靶体表面应力分布更复杂且应力影响范围增大,内部应力场分布不规则,也出现随着深度增大应力先增大后减小的趋势。

(4) 入射角θ=15°,射流速度v≤375 m/s时,靶体内部应力变化较为平缓,对靶体材料疲劳寿命影响最小。射流速度每增大100 m/s,靶体内最大主应力出现最大值对应的入射角θ增加约2°。