顶部方形开洞对超高层建筑风荷载影响的大涡模拟研究

郑德乾,吴俊昊,马文勇,马志敏,潘钧俊

(1.河南工业大学 土木工程学院,郑州 450001;2.石家庄铁道大学 土木工程学院,石家庄 050043;3.广州富力地产(重庆)有限公司,重庆 400030;4.中国建筑第八工程局有限公司,上海 200135)

风荷载是超高层建筑设计的主要控制荷载之一[1]。对建筑局部形状修正或选取合理的建筑外型等气动措施,能以较低的成本有效减小建筑风荷载及风效应,节约造价并改善结构的舒适性,被广泛应用于超高层建筑设计中[2-3]。

角部处理是典型的局部外形修正的气动优化措施。采用风洞试验方法,国内外学者研究分析了斜切角、凹角、倒角及圆角等多种角部优化对方形截面超高层建筑气动力、横风向风致响应的影响,发现角部优化能够在不同程度上减小横风向基底气动力系数,特别是切角率大于5%或圆角率大于15%时,横风向风致响应位移显著降低[4-8]。此外,方形截面超高层建筑沿高度方向采用锥形化处理,能够通过减小迎风面积而增大竖向漩涡脱落频率,横风向升力系数功率谱谱峰也会小幅下降,从而可以有效降低结构的横风向风荷载和风致响应[9-11]。

超高层建筑立面开洞也是一种相对有效的气动措施。王春刚等[12-14]通过风洞试验和数值模拟,研究了不同开洞率高层建筑表面风压随风向角的变化规律,结果表明:立面开洞可以减弱结构的静力风荷载,然而并非开洞率越大对风荷载的减小就越明显,存在最优开洞率使得建筑物所受平均风荷载最小。李永贵等[15-17]研究了开洞高层建筑风荷载幅值和频域特性,认为开洞可以降低结构洞口附近风荷载,其中上部开洞的减荷效果优于下部开洞,双向开洞效果好于单向开洞;陈伏彬等[18-19]指出大的开洞形式对降低顺风向平均基底弯矩的效果较好。利用高频天平测力风洞试验方法,马文勇等[20-22]较系统地分析了7种不同顶部开洞样式对结构基底的顺、横风向气动力和功率谱,以及风致响应的影响,发现不同顶部开洞样式对超高层建筑的气动特性,以及弯矩功率谱的峰值大小、横风向的卓越频率及风致响应都有较大的影响。上述研究大多采用风洞试验方法,研究顶部开洞形式对结构风荷载的影响,在洞口对风荷载的影响机理方面的讨论则较少涉及。

与风洞试验方法相比,CFD(computational fluid dynamics)数值模拟便于流场可视化,能够通过不同顶部开洞形式周围流场的对比,探讨造成风荷载分布差异的原因。基于Fluent软件平台,本文采用大涡模拟(large eddy simulation,LES)方法,对湍流边界层风场内2种顶部开洞超高层建筑模型进行非定常绕流计算,通过与马文勇等对比,验证本文数值模拟方法及参数的有效性,研究分析了顶部无、有开洞,以及开洞形式对结构表面风压系数的影响,并着重从周围时均和瞬态流场对比分析,讨论其影响机理。

1 计算模型尺寸及参数设置

为获取结构周围的脉动特性和瞬态流场信息,CFD数值模拟计算采用基于空间平均的大涡模拟方法。方形截面超高层建筑模型的宽高比为D∶H=1∶6,边长D=100 mm,模型几何缩尺比1∶500。考虑2种顶部开洞工况:封闭式方形开洞(T1模型)和敞开式方形开洞(T2模型),其中方形洞口大小50 mm×50 mm;作为对比,还考虑了顶部无开洞的标准方柱模型工况(T0模型)。上述详细的洞口尺寸如图1所示;研究对象处于B类地貌。当来流沿洞口方向时,顶部开洞对结构总体平均风荷载和横风向基底弯矩均方根减弱效果最显著,本文选取该风向进行风荷载影响及机理分析。

(a) 风洞试验模型与测点布置

为验证本文数值模拟方法及参数的有效性,首先对封闭式方形开洞方柱T1模型分别进行了大涡模拟计算和风洞测压试验,其刚性模型测压试验风洞在石家庄铁道大学STDU-1风洞试验室低速试验段进行,试验段尺寸为24 m(长)×4.4 m(宽)×3 m(高),风洞试验模型及压力测点布置图如图1(a)所示,限于篇幅,下文仅给出用于本文对比分析的试验结果。

大涡模拟计算中,为确保绕流后的流动充分发展,计算域大小取为:98D×36D×36D(流向x×展向y×竖向z),阻塞率不超过3%。计算域的离散采用基于区域分块技术的非均匀结构化网格,计算域底面和建筑物表面的近壁区网格采用加密处理,网格伸展率不超过1.2;为验证LES结果的网格无关性,对封闭式方形开洞方柱T1模型考虑了3套不同分辨率的网格,具体参数如表1所示。

表1 计算工况及网格参数Tab.1 Case details and mesh scheme

采用速度入口(velocity-inlet)边界条件,大涡模拟入流脉动的合成通过将RANS自保持边界条件[23]引入STG(synthetic turbulence generator)方法[24]实现。与MDSRFG[25]、NSRFG[26]方法类似,STG方法也以Karman谱为目标谱,故模拟风速谱一致性更好。不同的是,前两种方法需要预先合成或复杂UDF编程施加,而STG则为Fluent内置方法,仅编写RANS自保持边界条件即可;此外,STG方法用于标定脉动风速场的修正参数又来自于作为LES大涡模拟初始流场的RANS定常计算,因此,STG方法更为快捷且精度相对较高。来流风速U(z)、湍动能k(z)和湍动能耗散率ε(z)分别为

(1)

(2)

(3)

式中:冯·卡门常数K=0.42;模型常数Cμ=0.09;其他风场参数值由风洞试验数据拟合得到,其中摩擦速度u*=0.577 m/s,地面粗糙高度z0=2.25×10-4,常数C1=-0.416 2、C2=0.186 7。出流面采用压力出口(pressure outlet)边界条件,侧面和顶面均采用对称(symmetry)边界条件,计算域底面和建筑物表面采用无滑移壁面(wall)。

首先,采用基于时间平均的RANS(Reynolds averaged Navier-Stokes)方法,对考虑工况采用Realizablek-ε湍流模型进行定常绕流数值模拟计算,近壁区采用非平衡壁面函数,动量方程、湍动能及湍动能耗散率方程均采用二阶精度离散格式,压力速度耦合方式采用SIMPLEC算法,控制方程收敛残差设置为5×10-4。然后,进入LES大涡模拟计算,采用Dynamic Smagorinsky-Lilly亚格子模型,空间离散格式为二阶精度Bounded central differencing;时间离散为二阶隐式格式,时间步长Δt=0.000 5 s,经计算,96%以上网格单元的柯朗数(Cell Courant number)不超过1.0,满足CFL准则要求。大涡模拟总时长6.5 s,共13 000个时间步,统计分析中选取后10 000个时间步数据。

2 结果与讨论

建筑表面风压均以模型高度H处来流平均风速无量纲化

(4)

式中:Cpi为测点i的风压系数;Pi为测点i的风压;ρ为空气密度,值为1.225 kg/m3;UH为模型高度H处的来流平均风速。风压系数均值Cp,mean和根方差值Cp,rms分别表示平均风压系数和脉动风压系数。

2.1 湍流边界层风场模拟结果比较

首先,将大涡模拟所得入流面与模型中间位置处风剖面和距离地面H高度处的脉动风速谱,分别与GB 50009—2012《建筑结构荷载规范》[27]、试验风剖面及Karman谱进行比较,如图2所示。

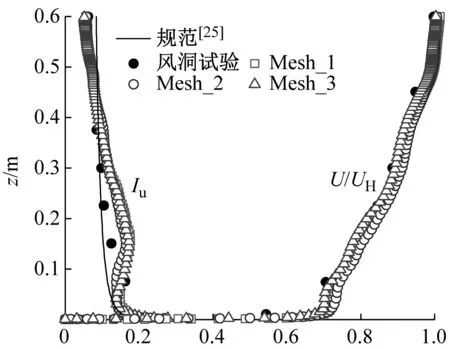
(a) 风剖面

由图2可见:大涡模拟所得B类风场平均风剖面与风洞试验和规范结果具有较好的一致性。湍流度剖面总体上能反映规范、风洞试验变化趋势,在0.3 m以下高度范围高于规范和试验值,这主要是由于近地面处大都为小尺度涡的复杂运动,对离散网格的要求更高,加之近地面处湍流度较大且梯度变化也较剧烈所致;但在0.3 m以上高度范围,大涡模拟所得湍流度剖面与规范、风洞试验值吻合较好。数值模拟所得脉动风速谱在低频处均能够与Karman谱较好吻合,在高频处也能够满足捕捉到工程中较关心的惯性子区段,无量纲频率超过1.0处的衰减是由于网格滤波效应所致。3套网格的风剖面和风速谱均比较接近,说明进一步加密网格对风场模拟精度的改善不明显。总的来说,本文大涡模拟方法及参数能够较好地重现湍流边界层风场,从而确保了风荷载模拟结果的可靠性。

2.2 模型风压系数大涡模拟与试验结果的比较

图3为3套不同分辨率网格情况下,封闭式方形开洞方柱T1模型在z=0.88H高度开洞位置处,测点平均和脉动风压系数的大涡模拟与风洞试验结果比较。

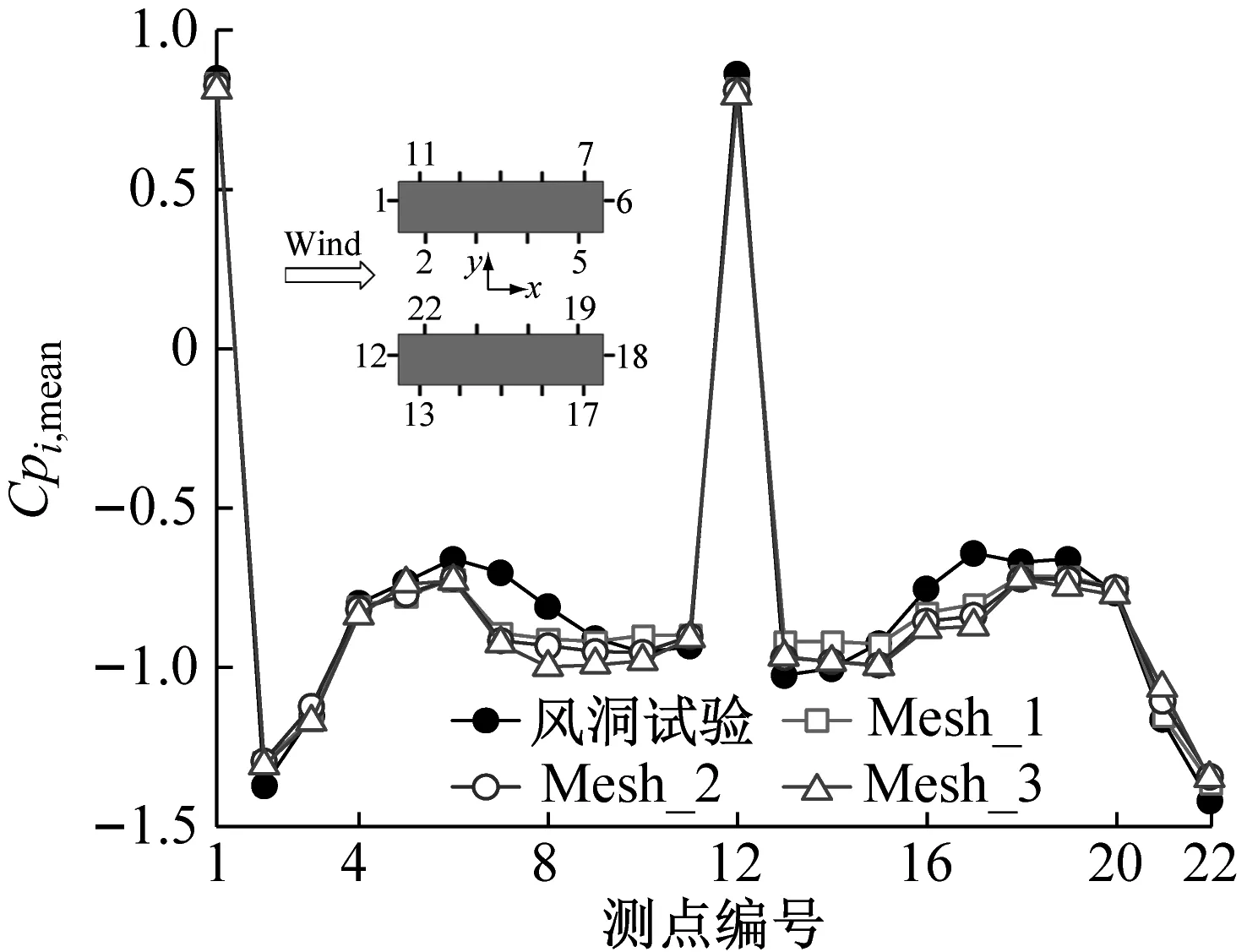
(a) 平均风压系数

由图3可见:在考虑的来流沿洞口方向情况下,基于3套网格大涡模拟所得结构表面平均风压系数与风洞试验结果均吻合相对较好;数值模拟所得脉动风压系数在洞口边角处(测点2～3、21～22)和洞口外侧(测点8～11)的复杂流动分离区与风洞试验结果偏差稍大,在其他位置测点的差别不大且总体变化趋势一致。上述偏差的产生是由于受建筑迎风边缘、洞口内壁和底面边缘处分离涡的共同作用,使得这些区域流动复杂、风压梯度变化剧烈所致。对比3套网格结果可知:采用近壁面首层网格无量纲距离y+较大(y+>5.0)的Mesh_3稀疏网格时,与试验结果的最大误差可达18.6%;加密网格至y+<5.0,Mesh_2中等网格和Mesh_1较密网格,最大误差可分别缩减至11.1%和10.0%。虽然理论上进一步加密网格至y+≈1.0(Fluent建议值)可更好地捕捉近壁面流动而提高模拟精度,但也将带来更为庞大的网格数量。因此,综合考虑湍流边界层风场和结构表面风压的预测精度及计算效率,本文后续工况均采用壁面y+<5.0的中等分辨率Mesh_2网格。

2.3 顶部开洞对方柱表面风压分布的影响

为了探究顶部开洞样式对建筑表面风压的影响,本节给出了来流方向与洞口朝向一致情况下,标准方柱T0(不开洞)、顶部封闭式开洞T1和敞开式开洞T2模型的平均和脉动风压系数等值线云图,分别如图4和图5所示,考虑到结构对称性,侧面风压系数分布仅给出右侧面结果。

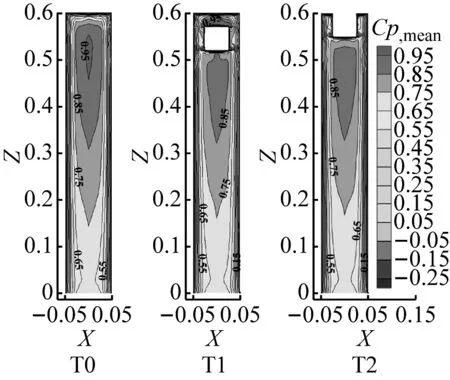
(a) 迎风面W

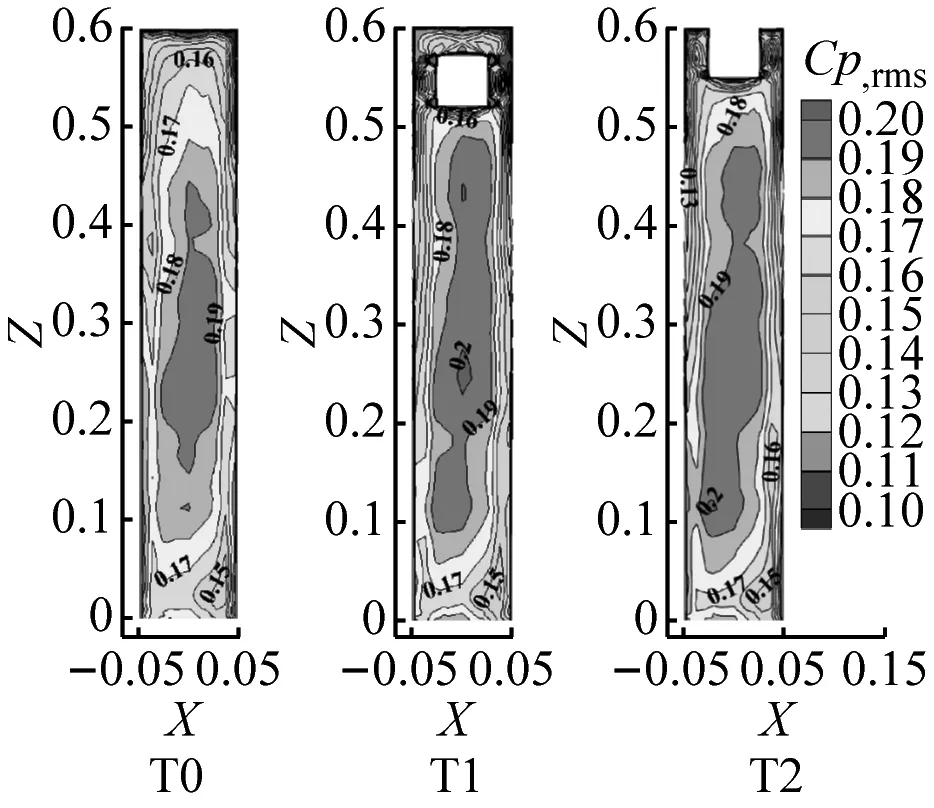
(a) 迎风面W

由图4可知平均风压系数比较可见,总体上,3种工况模型迎风面均以正压(风压力)为主,但在迎风面边缘位置(两侧、顶部、洞口周边)、建筑侧面和背风面则为负压(风吸力)。顶部开洞后,原本受洞口位置建筑表面阻挡的来流直接穿过洞口(见图6、图7),使得洞口边缘处因流动分离出现较大风压梯度,并主要影响了顶部洞口z=0.5～0.6 m高度局部区域的风压分布:

(a) 标准方柱T0

(a) 标准方柱T0

(1) 对于T0、T1和T2模型,上述洞口区域迎风面的面积加权平均风压系数值分别为0.65、0.49和0.58,背风面为-0.81、-0.73和-0.80,侧面分别为-0.96、-0.91和-0.90。可见,2种顶部开洞情况均能够减弱洞口附近局部风荷载,其中顶部封闭式开洞(T1)更为显著;此外,最大压力(吸力)作用点位置也发生了一定变化,封闭式开洞使得迎风面最大正压作用点位置上移,侧面最大负压位置变为集中在靠近背风侧的上部局部小范围区域(图4(c)右上角)。造成上述影响的主要原因是,当来流沿洞口直接被引入到背风面后,尾流区附近的大尺度涡被打散,并在背风面洞口附近形成小尺度旋涡,以及建筑侧面的分离涡尺度变小,且更贴近壁面,涡旋更加分散所致(见图6、图7)。

(2) 在洞口内表面的相同位置(洞口侧面、底面),T1和T2模型的负平均风压系数最值均靠近建筑迎风面(数值可达-1.2),但具体发生位置、作用范围及分布情况明显不同。在洞口侧面靠近建筑迎风面部位(图4(d)左侧区域),T1和T2模型产生了形状和面积大致相同的负风压系数最值,这是由于洞口处流动分离所致;不同的是,T1模型侧面下部也出现了较大面积的负压最值。在洞口底面,两个开洞模型的负压分布差异更为显著,其中T1模型的负压梯度较大,风压系数最值为-1.2,作用范围涵盖建筑迎风边缘至洞口底部1/2面积区域,而T2模型的负压值则仅为-0.85～-0.90。造成上述洞口内表面风压分布差异的原因,是由于T1模型洞口为封闭式,洞口顶盖的存在使得狭管效应引起的气流加速现象更为显著,洞口中心处最大风速可达相同高度来流风速的1.39倍,导致洞口内的4个壁面均承受较大的负压作用(见图7、图8)。

(a) 标准方柱T0

图5为脉动风压系数的比较结果,由图5可知,总体上,3种模型背风面均在中部高度范围内出现脉动风压最小值区域,方柱表面的两侧边缘处、洞口边缘位置受分离流的影响产生较大的风压脉动(最大值为0.35)。具体为:

(1) 顶部开洞总体上也是减弱了方柱表面的风压脉动,这与其对平均风压系数的影响类似。不同的是,迎风面洞口边缘处因流动分离出现了较大的风压脉动,尤其是封闭式开洞T1模型,这是由于洞口内的气流受上部洞口边缘的影响,狭管效应产生的加速效应明显(见图8);此外,开洞也使得侧面的分离涡形态及分离点位置发生了变化,导致侧面脉动风压系数最值区域及其位置有所不同。

(2) 对于2个开洞模型的洞口内表面来说,两侧的脉动风压系数最大值均可达0.35;在洞口底面,T1模型最大值为0.35且梯度较大,T2模型则仅为0.23,与图4的平均风压系数比较结果类似。2个顶部开洞方柱模型的洞口大小尺寸相同,而洞口顶部封闭情况不同,其内表面平均和脉动风压系数分布情况的异同,也反映了封闭式、敞开式洞口对穿过其内部气流流态的不同,下文将从时均和瞬态流场角度进行分析。

2.4 时均流场影响分析

根据上文分析可知,顶部开洞使得方柱表面风荷载有所减弱,尤其是T1模型更为明显。下面将通过对比3种模型典型位置处周围的时均流场来分析顶部开洞对风荷载的影响机理。

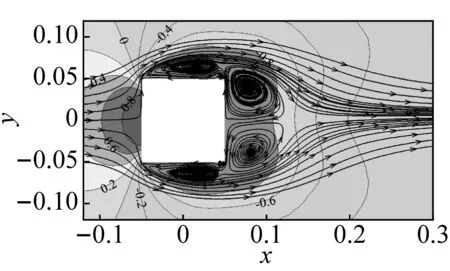
标准方柱T0与T1、T2模型z=0.93H高度(开洞位置)处水平截面的时均流线与平均风压系数云图,如图6所示。由图6可知,总体上,来流垂直作用于迎风面,均在迎风前缘边角处发生流动分离,形成的分离剪切层在湍流卷吸作用下于两侧面发生流动再附,产生对称的分离涡后,在背风面生成对称尾涡。具体来说,不同开洞形式方柱,其两侧分离涡大小、涡核心位置、分离再附位置,以及尾流区旋涡尺寸不尽相同,主要表现为:

(1) 在方柱的侧面位置,T0模型除形成剪切层外,还形成了1个与背风面分离涡连接的大尺度分离涡,涡核心距壁面0.16D,作用范围x=-0.05 m～0.04 m;在方柱下游角部近壁面位置,还形成了独立存在的小尺寸分离涡,涡核心距壁面0.05D,范围x=0.04 m～0.05 m,该分离涡的涡核心位置处也是图4(c)侧面最大负压处。

相比之下,顶部开洞2个模型侧面剪切流扩散角度变小,导致侧面均仅形成1个中小尺度分离涡(小于T0模型),涡核心更加贴近壁面,距离均减小为0.09D,比标准方柱T0模型减小了43.8%,使得z=0.5～0.6 m开洞区域的面积加权平均风压系数值均低于标准方柱T0模型。此外,2个模型侧面分离涡的范围差异也比较显著,封闭式开洞T1模型分离涡范围与标准方柱T0模型大致相当;而顶部敞开式T2模型分离涡范围仅为x=-0.05～0.001 3 m(比T0和T1模型缩小了43%),这是由于T2模型的顶部洞口的两侧与短边迎风的矩形断面类似,侧面分离泡直径被压缩,分离剪切层发生了明显再附现象,导致T2模型侧面洞口区域脉动风压梯度最明显,且下游位置(图5(c)右上角)的脉动风压系数值也最小(T0、T1和T2模型,脉动风压系数值分别为0.25、0.23和0.19)。

(2) 在背风面,标准方柱T0在背风面尾流区形成了两个对称的大尺度涡,涡核心距壁面为0.3D,距方柱中心处0.42D。顶部开洞后,部分气流由洞口流过,在洞口边缘处形成了流动分离,使得洞口边缘部位产生较大的负风且风压梯度也较大。顶部开洞处理减小了方柱的剪切流扩散角度,使得尾流区段变窄。T1模型洞口两侧的墙肢后均形成了尺度相当的2个分离涡,而T2模型则形成了1个较明显的分离涡。上述差异是由于封闭式开洞T1模型洞口顶盖的存在使得洞口内的风加速现象更加显著;而敞开式开洞T2模型则在距离迎风面0.2D处即发生了一定的回流(见图6(c)),导致T2模型洞口底面的风压梯度及数值均低于T1模型(见图4(d)、图5(d))。

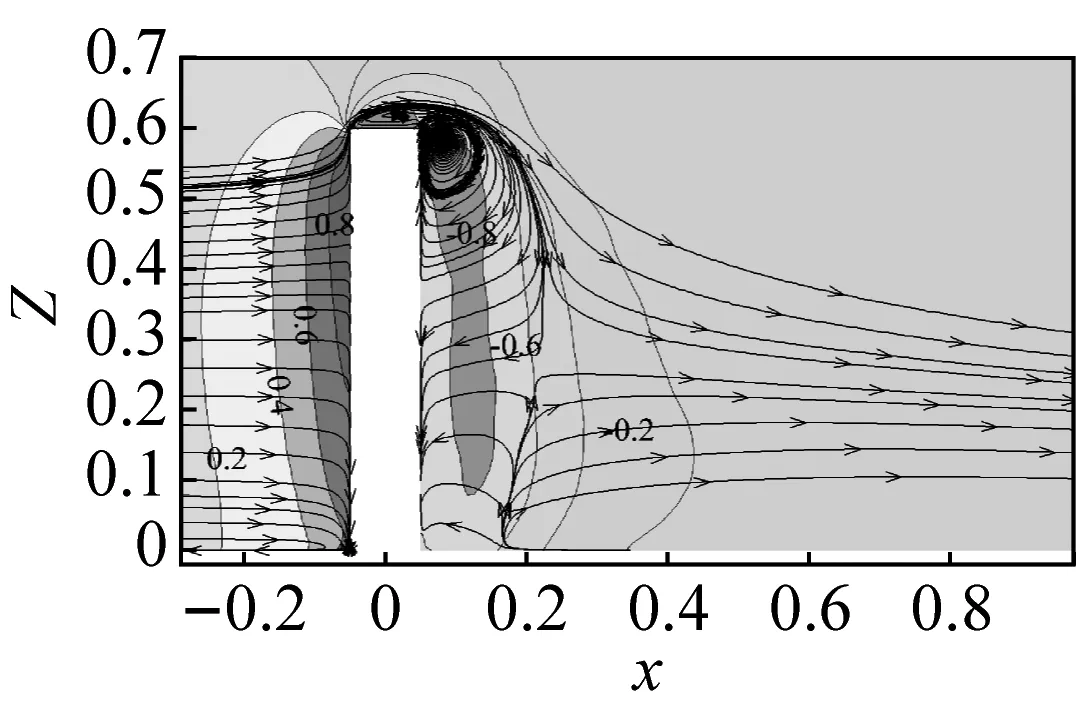
图7为3种模型在y=0纵剖面的时均流线与平均风压系数云图,可以看出,除建筑物顶部的时均流场局部稍有差别外,其他区域基本一致;下面分别从迎风面、顶部、背风面三个区域进行分析:

(1) 标准方柱T0大致以2/3H高度为分界点,迎风面上方气流在建筑物顶部形成流动分离,分界点以下气流趋向于下部流动,形成底部回流并生成小尺度的马蹄涡,分界点两侧气流沿水平向流动绕过侧面在建筑物尾流区形成两个反向的水平大尺度分离涡(结合图8可知)。与标准方柱T0模型相比,2种顶部开洞方柱的气流分界点均向下移动至距离地面7/12H高度处,这与顶部开洞后更多的上部气流可以从洞口处流过有关,底部回流区段缩减与(见图8)建筑物前方包络柱底部条状涡带变少现象相对应,这是导致顶部开洞方柱迎风面中上部区域的风压减小(见图4(a))的原因。

(2) 在方柱顶部区域,迎风面与背风面顶部两侧边角处各形成一个分离点。标准方柱T0的顶部和背风面顶部区域各自生成一个相互独立的分离泡,产生分离泡的区域对应图4a中最大负压值区。在背风面区域,受背风面顶部分离涡的影响,绕过方柱的气流均向下部流动,当方柱顶部开洞后,洞口流出的气流将背风面的旋涡打乱,对于封闭式开洞T1模型,其背风面顶部形成了2个不同尺寸分离泡,分别位于方柱顶面和洞口底面附近,使得方柱背风面开洞处的旋涡能量更加分散,相应区域的平均和脉动风压也明显减弱,在3个模型中其风吸力最小、脉动性最弱,而远离洞口的区域无影响;敞开式开洞T2模型类似于高度略低的标准方柱,其顶部和背风面上部区域2个分离泡与标准方柱T0类似,但尺度小于标准方柱,使得背风面同位置区域的风吸力略低于标准方柱T0模型。

2.5 瞬态流场影响分析

图8为流场Q值取3 000情况下,标准方柱T0、顶部开洞方柱T1和T2模型周围的三维瞬态涡量图,图8中采用流向平均风速(以模型顶部来流平均风速UH无量纲化)对涡结构进行着色。由图8可知,整体上,气流流经方柱后,沿方柱两侧和顶部边缘处发生分离,流动分离区域的风速显著增大,方柱侧面形成了不同尺度的条带状分离涡,在尾流区与来自顶部的分离涡相互掺混,构成了复杂的三维涡结构,且在方柱的尾流区均已形成了较明显的涡道。对比3个模型工况,其周围的涡形态、数量及运动趋势有所差别:

(1) 在迎风面底部区域,3种模型前方均出现条状涡带,绕过方柱两侧并生成紧贴壁面的分离涡,这是由于地面摩擦效应产生的逆压梯度,使得下部气流抵达方柱迎风面后反向运动而形成的底部回流所致,靠近方柱的条状涡带逐渐减小,呈现出一种包络方柱底部的现象,这是方柱迎风面底部出现较大风压的原因(见图4(a))。

(2) 方柱顶部开洞后,迎风面边缘的流动分离点向下移动,方柱顶部的涡量减小,原本受迎风面阻挡的气流从洞口位置穿过,使得开洞T1和T2模型侧面的分离涡尺度,以及流动分离产生的风速加速现象均低于无开洞的标准方柱T0模型,因此方柱侧面的平均和脉动风压最大值也均低于T0模型。此外,开洞后形成了狭管效应,使得穿过洞口的气流产生了加速,打乱了背风面的大尺度涡流,并在洞口附近及背风面形成了若干贴近壁面的小尺度涡,能量更加分散,使得2种开洞方柱背风面的整体风压均有所减弱。具体地,对于封闭式开洞T1模型,洞口的顶盖使得穿过洞口的风速加速效应更为显著,在洞口内壁产生较大负压;敞开式开洞T2模型在开洞处由于发生回流现象(见图6(c)),洞口内风速增大相对不显著,因此,内壁负压的增大也不明显,但背风面的尾流涡有向后上方运动的趋势,这是造成T2模型在开洞处顶部两角部区域的脉动风压增大的原因(见图5(b))。

3 结 论

(1) 采用基于自保持边界条件的STG方法合成大涡模拟入流脉动,数值模拟所得风剖面及脉动风速谱与目标风场基本吻合;大涡模拟所得封闭式方形开洞方柱的平均、脉动风压系数均能与风洞试验结果具有较好地一致性,说明本文大涡模拟方法及参数能够满足超高层建筑非定常绕流风场及风荷载预测的精度要求。

(2) 对于来流平行开洞方向的情况,方柱顶部开洞后,减小了方柱的迎风受风面积,部分来流经洞口进入尾流负压区,影响了流动分离点位置、剪切流扩散角度及流动再附现象,侧面分离涡更贴近壁面,尾流明显变窄;开洞处的狭管效应造成洞口内的风速急剧增大,尾流区大尺度旋涡被冲散,能量更加分散,减弱了方柱表面的风压,这对减小整体风荷载和风致振动尤其是涡激振动都有积极的意义。由于开洞边缘部位出现新的流动分离点,使得该位置处的平均及脉动风荷载变大,特别是顶部敞开式开洞在背风面存在显著的边缘效应现象,易引起围护结构的局部风致破坏,应引起注意。

(3) 对于顶部开洞方形截面超高层建筑,相同开洞面积和形状时,封闭式开洞对减弱表面风压的效果优于敞开式开洞,这与顶部敞开式开洞两侧类似于短边正迎风的矩形断面,侧面分离泡被压缩,分离剪切层发生再附,在开洞处出现回流现象有关。