安装座焊接结构双轴拉伸模拟件设计

2023-09-19吴振豪刘鹏飞

焊接 2023年9期

吴振豪,刘鹏飞

(中国航发贵阳发动机设计研究所，贵阳 550081)

0 前言

焊接工艺在航空发动机中具有广泛的应用，尤其是在航空发动机燃烧室机匣上存在着大量的安装座焊接结构。由于燃烧室在实际的工作当中，其机匣外壳承受着多种载荷的作用，如机匣内外压力差、气体轴向力、由机匣后安装边带来的扭矩、机匣外壁各种安装座接头载荷及外机匣上所有构件的质量惯性力等[1]，导致安装座周围有着复杂的应力应变状态，从而也使得安装座焊缝成为了多轴疲劳破坏的薄弱部位之一。研究安装座焊接结构的多轴疲劳性能，对于精准预测航空发动机焊接结构的疲劳寿命有着至关重要的意义。

目前，国内外针对航空发动机燃烧室机匣安装座焊缝疲劳性能的研究的方法大都是以有限元模拟和模型机匣结构件的试验相结合为主。杨眉等学者[2]学者通过有限元模拟与试验相结合的方式，研究了航空发动机燃烧室机匣上的安装座在极端工况下的破裂安全性。Sarangi等学者[3]对典型涡扇发动机的环形燃烧室机匣进行了有限元模拟和物理测试，研究了机匣上安装座构件的疲劳寿命情况。田海涛等学者[4]通过氩弧焊接机匣的疲劳试验研究了机匣及其安装座焊缝处的疲劳寿命。尽管采用接近真实比例的燃烧室机匣模型进行试验能够得到比较准确的安装座焊缝疲劳寿命结果，但是这样的试验成本较高，且一次性试验得到疲劳寿命具有偶然性。对此，很多学者采用常规的标准疲劳试件代替结构件。刘健[5]通过数值模拟和单轴疲劳试验，采用场强法和临界面法对某型发动机燃烧室机匣安装座焊缝疲劳寿命进行了预测。公维勇[6]运用蒙特卡罗法建立了疲劳寿命预测模型，并结合GH4169焊接接头单轴疲劳试验得到了燃烧室机匣安装座焊缝处的疲劳寿命。王金生[7]根据单轴静拉伸试验，单轴疲劳寿命试验及疲劳裂纹扩展试验的试验结果，结合有限元计算结果研究了燃烧室外机匣和轴承座2种焊接结构的疲劳性能。

标准疲劳试件并不能真实地反映安装座焊缝处疲劳损伤特征[8 - 9]。因而，国内外通常将标准疲劳试件和实际构件相结合，设计出特征结构模拟件对某一特定构件的疲劳寿命进行考核。使用模拟件进行试验能够令疲劳寿命预测结果有较高的可信度，根据航空发动机燃烧室机匣工作时的载荷工况，安装座焊接结构的受载特征主要是双轴拉伸载荷，其模拟件的设计将以双轴拉伸试件为基础。早在上世纪60年代，就有学者[10]开始使用十字形双向拉伸试件确定在双轴载荷作用下材料的初始和后继屈服面。此后，随着双轴拉伸试验机的发展，双轴拉伸试验开始逐渐应用广泛，十字形双向拉伸试件的设计也产生了很多分支，诸如十字花型，中心减薄型及十字臂上开缝型三类典型的十字形试件类型。第一类试件中，较为典型的有Kreiβig等学者[11]和Müller等学者[12]所设计的试验件，他们均在相邻十字臂之间倒角上进行更改，使其变更为一个向内凹的缺口，以此达到减小倒角的应力水平的效果。而对于第二类试件，较为典型的有Lin等学者[13]和Welsh等学者[14]所设计的试验件，均通过减薄中心试验区的厚度，来增大中心区域的应力水平，但是这类试验件往往达不到预期效果。目前，第三类试件被广泛应用在双轴拉伸试验件上，Makinde等学者[15]、Kuwabara等学者[16]、Ferron等学者[17]及Wu等学者[18]所设计的试验件都是典型的在十字臂上开缝的双向拉伸试验件，通过在十字臂上开设若干细缝来增大中心区域的应力水平同时降低相邻十字臂之间倒角处的应力。

综合上述，文中将以十字花型双轴拉伸试件为基础，根据航空发动机机匣安装座焊接结构的几何和受载特征，设计出一种用于预测安装座焊缝疲劳寿命的模拟件。

1 模拟件设计方案

1.1 模拟件设计原则

研究对象为航空发动机燃烧室机匣安装座的焊接结构，而在实际工作中机匣主要承受轴向力p0与内压力p，因此，外机匣上任意位置在这2种载荷的作用下受到的应力状态如图1所示。

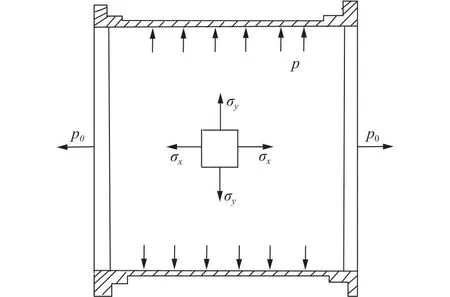
图1 机匣上一点应力状态

由应力状态示意图可以看出，机匣上任意位置均会受到2个应力分量σx和σy的作用，类似于双轴拉伸应力状态。因此，所设计的疲劳模拟件应尽可能实现相似的应力状态，故而采用十字形双轴拉伸试件作为模拟件的设计基础，能够使试件的十字中心试验区满足此应力状态。为研究机匣安装座焊缝的疲劳寿命，需要在试验区内加工一个类似安装座的焊接结构，以此达到模拟机匣安装座焊缝疲劳损伤状态的效果。此外，实际机匣安装座焊缝的疲劳破坏机理尤为复杂，基于安装座焊接结构特殊的几何特征和焊接工艺，模拟件的设计还需要满足以下3点设计原则：①模拟件的焊缝形式与机匣安装座几何相似，即均采用环焊缝；②模拟件焊缝加工的工艺条件与机匣安装座焊缝相同，即均采用电子束焊接。由于该文是针对燃烧室机匣安装座电子束焊接结构的疲劳寿命进行的研究，因此，模拟件的焊缝也采用电子束焊接工艺进行加工；③在试验条件下，模拟件焊缝的考核部位尽可能与机匣安装座环焊缝的应力分布规律接近。安装座焊缝的应力分布会随着燃烧室机匣工况及安装座几何结构的改变而随之改变，因此，模拟件焊缝需要参考机匣典型安装座的应力分布规律进行设计。

1.2 几何等效分析

航空发动机燃烧室机匣上安装座的焊缝大都为圆环形，如涡轮孔探仪座、燃烧室孔探仪座及CDP接嘴座等，结构均为圆柱形带通孔的双层凸台式结构，因此，模拟件的安装座焊接结构的设计应同样以圆柱形作为设计基础，以此保证几何特征对焊缝应力状态的影响是相同的。

1.3 模拟件尺寸设计

在传统的十字形双轴试件的基础上结合设计原则和几何等效分析，设计出的安装座焊接结构双轴拉伸模拟件结构及相应结构尺寸参数如图2所示，待定尺寸中，中心试验区直径D1、安装座通孔直径D2、夹持臂与端面之间夹角ω为待优化尺寸，其余倒角尺寸随着这3个尺寸参数变化而进行调整。中心部分为安装座焊接结构，安装座周围一圈阴影部位为焊缝区域。

1.4 模拟件有限元模拟验证及分析

为了验证所设计模拟件的合理性，对安装座焊接结构双轴拉伸模拟件进行有限元模拟计算，同时分析模拟件的应力水平大小及应力分布情况，图3为模拟件有限元模型（根据对称性取1/4），中心试验区的网格尺寸设置为0.1 mm。由于该模拟件用于高周疲劳试验，因此，只考虑弹性范围内的应力变化，采用GH4169材料及其焊接接头的弹性力学性能参数。

图3 模拟件1/4有限元模型

分别在模拟件的x轴与y轴的夹持面施加拉伸载荷，这2个轴向拉伸载荷的比值定义为双轴比，如式（1）所示：

式中：Fx是x轴向载荷；Fy是y轴向载荷。分别进行双轴比γ为0.8，0.9和1.0下的有限元计算。经过计算所得到的模拟件的1/4模型的等效应力云图如图4～图6所示（文中等效应力均为Mises等效应力）。可以看出双轴比γ为1.0时，试验区的应力分布情况与典型燃烧室机匣安装座周围的应力分布情况相一致[6]。因此，机匣安装座焊缝的应力状态可以通过该文所设计的模拟件在双轴比γ为1.0的加载条件下近似等效。

图4 γ = 0.8的等效应力计算结果

图5 γ = 0.9的等效应力计算结果

图6 γ = 1.0的等效应力计算结果

2 模拟件优化方法

2.1 优化设计目标

根据模拟件的有限元计算，为保证焊接接头径向宽度上的应力分布均匀，同时避免受到应力集中的影响，以此达到考核环形焊缝疲劳性能的目的，该文提出3点优化目标：①提高环焊缝沿着径向的应力分布的均匀性（图7中焊缝径向所指位置）；②尽可能降低图7中所示的减薄区与安装座根部过渡倒圆角的应力集中；③模拟件其他部位的应力水平低于焊缝应力水平。

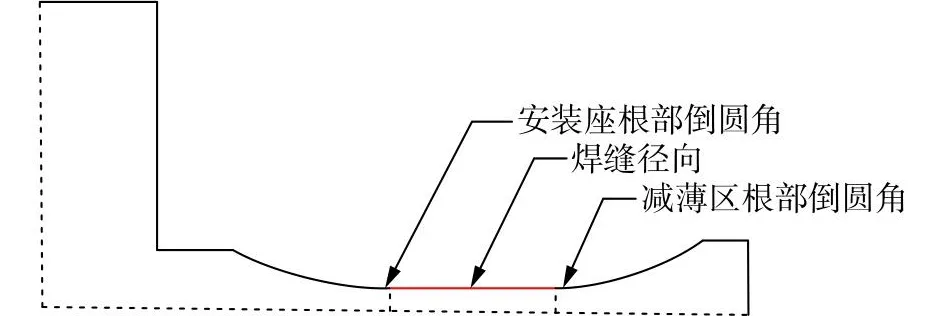
图7 模拟件焊缝径向示意图

2.2 理论模型

为了定量分析模拟件是否达到了上述优化目标，该文以Demmerle等学者[19]提出的关于优化十字形双轴拉伸试验件的理论模型为基础将优化目标参数化，分别采用3种理论模型计算出来的数值代表优化的结果。根据优化目标中第一个要求，通过计算焊缝应力的标准差定义参数I，从而评估模拟件焊缝的均匀性。在有限元计算中，该参数I可以表示为式（2）：

式中：n代表焊缝径向宽度上的单元数；S为该焊缝径向所有单元等效应力的标准差；σvm,n为第n个单元的等效应力值；为焊缝径向所有单元的等效应力的平均值。该公式的含义为焊缝径向等效应力的离散程度，评估参数I的值越高代表焊缝径向应力均匀性越差。

根据优化目标中第二个要求，由于倒角根部存在的应力集中无法消除，为此要尽可能的降低倒角根部与焊缝等效应力的差值水平，将该差值水平定义为参数J，并通过焊缝与倒角根部的最大等效应力的比值来计算，如式（3）所示：

式中：(σvm)max为倒角根部的最大等效应力；(σvm)1为焊缝的最大等效应力。该公式通过参数J的数值判定倒角根部的应力集中对焊缝出现疲劳破坏影响的程度，数值越高代表倒角根部的应力集中对焊缝区疲劳破坏的干扰越大。

对于优化目标中第三个要求，可以设定一个惩罚因子P判定除焊缝之外的非关心部位的应力水平是否对试验有不利的影响，P的数值根据非关心部位的最大等效应力(σvm)2与焊缝的最大等效应力 (σvm)1的比值Q而定，数值越高代表非关心部位的应力水平越大，如式（4）所示：

将上述3个评估参数求和，即可得到每种模拟件的综合评估参数C，如式（5）所示。同理，综合评估参数C的值越小代表越接近优化目标。

2.3 模拟件尺寸优化步骤

该文将夹持臂与端面之间夹角ω，中心试验区的直径D1，安装座的通孔直径D2变化3种尺寸参数作为优化参数，通过改变这3个优化参数，讨论模拟件焊缝处及其他部位的在载荷双轴比为1.0的条件下的应力变化规律，优化求解步骤如下：①首先讨论D1在36.5～45.5 mm的范围内变化情况下，模拟件在哪种D1下最接近优化目标，同时使焊缝径向宽度保持在3.5 mm；②再讨论ω在50°～80°的范围内变化情况下模拟件整体的应力水平变化规律；③最后在3～9 mm的范围内改变D2，分析通孔直径D2对模拟件整体的应力水平的影响，根据影响结果选择出最优的模拟件尺寸。上述优化求解步骤中各个优化参数的尺寸变化范围均根据加工的便利性及试验设备的参数要求得出，通过计算各个模拟件的各项评估参数，根据参数的数值判定模拟件是否得到了优化，从而得到最终经过优化后的模拟件的尺寸。

3 模拟件优化及仿真结果分析

3.1 中心试验区直径D1的影响规律分析

保持基础模拟件的其他尺寸不变，将中心试验区的直径更改为36.5 mm，39.5 mm，42.5 mm和45.5 mm，同时使焊缝的宽度保持在3.5 mm左右。分别对这3种模拟件进行有限元计算，选取x轴焊缝径向路径单元有效应力σeq与该路径上最大等效应力的σmax比值（应力比）进行分析对比，结果如图8所示。从应力分布曲线的变化中可以发现，焊缝的等效应力变化呈两端高而中间低的特征。4种模拟件的焊缝应力水平都是以单调递减为主要变化特征，且随着D1的减小，递减的幅度逐渐增大，也代表着均匀度随之降低。

图8 不同D1下焊缝径向等效应力分布变化

为了更准确地讨论D1对于模拟件应力分布的影响，分别计算每种模拟件的评估参数并进行对比，对比结果如图9所示。从图中P的变化规律可以看到，随着D1的增大，评估参数P也随之增大，意味着非关心部位的应力水平随之增大，且递增的幅度也在增加。从评估参数I的变化规律可以看出，当D1的值越低，焊缝应力的均匀度越低，但是均匀度的递减幅度也在降低。而从评估参数J的变化可以知道，在D1降低到39.5 mm的时候，对焊缝与倒圆角根部的应力水平差值的影响变得并不明显。根据综合评估参数C的数值可以判断，当D1为39.5 mm的结果是最优的。

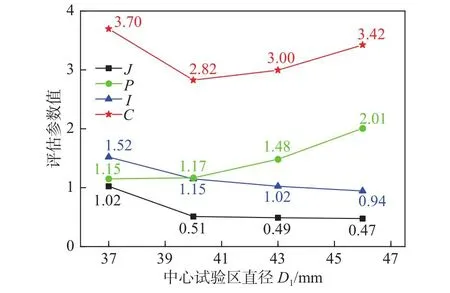
图9 不同D1下评估参数对比

3.2 夹持臂与端面之间夹角ω的影响规律分析

在确定D1最优值39.5 mm之后，继续讨论夹持臂楔形角度ω对模拟件应力水平和应力分布的影响规律。将ω由基础模拟件的60°分别取50°，70°和80°等不同值，对修改后的4种模拟件分别进行有限元计算，选取x轴向焊缝径向路径（图8b）应力比进行分析对比，结果如图10所示。由图10的试验区径向的应力分布的变化能够看出，等效应力分布变化同样呈现两端高而中间低的特征，而随着角度ω的增大，减薄区根部倒圆角的应力水平在不断减小。对比4种模拟件焊缝应力水平的变化可知，随着ω的增大，递减的幅度随之增大，意味着均匀度也在降低，且ω为50°的时候焊缝应力的均匀性明显优于另外3种情况。而从焊缝与根部倒圆角的应力水平对比可以看出，4种模拟件的焊缝与根部倒圆角的应力水平差值均在5%以内，并且随着ω的增大而增大。

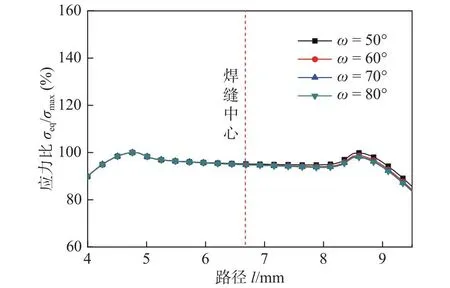
图10 不同ω下焊缝径向等效应力分布变化

分别计算每种模拟件的评估参数进行对比，对比结果如图11所示。从图中评估参数J，P，I的变化规律可以看到，随着ω的增大，3种参数也随之增大，而评估参数P的递增的幅度变化更为明显，这表明当ω较高时对非关心部位的应力水平影响很大，而对焊缝应力均匀度及与减薄区根部倒圆角之间的应力水平差值的影响很小。根据综合评估参数C的变化可以知道，ω越小越接近优化目标。因此，结合模拟件整体尺寸的需要，文中将ω的值设定为50°是最接近优化目标的。

图11 不同ω下评估参数对比

3.3 安装座通孔直径D2的影响规律分析

该节将使用与前两节相同的分析方法进一步讨论安装座通孔直径D2对模拟件应力水平和应力分布的影响规律。在其他尺寸均不变的基础上，将D2由基础模拟件的3 mm分别设置成6 mm和9 mm，并进行有限元计算，选取x轴向焊缝径向路径（图8b）应力比进行分析对比，结果如图12所示。由图可见，应力分布特点与之前相同，随着D2的增大，安装座根部倒圆角的应力水平在不断减小，而焊缝的应力水平随着D2的增大而减小。

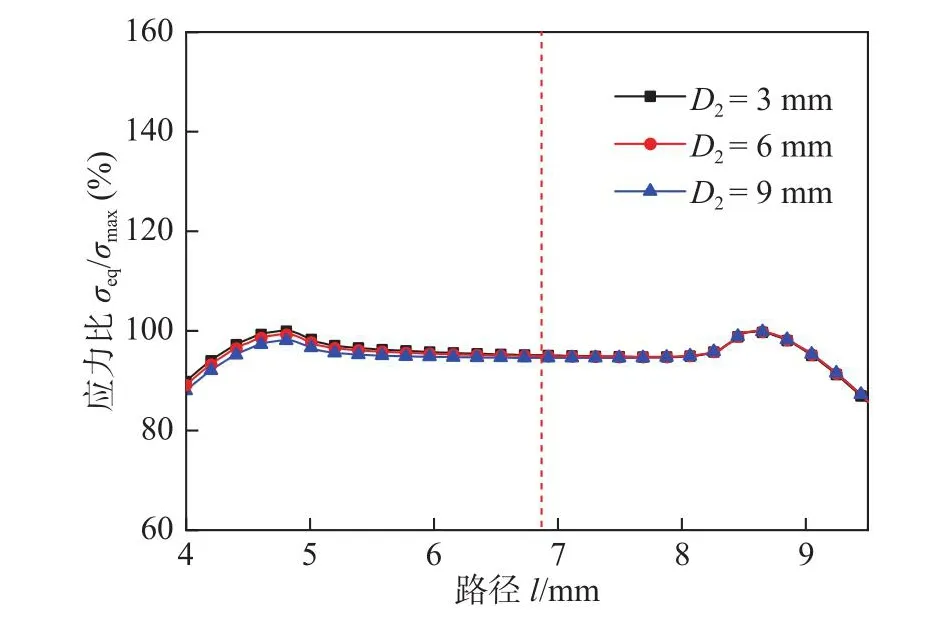
图12 不同D2下焊缝径向等效应力分布变化

计算3种模拟件的评估参数并分析其变化规律，如图13所示。从图中评估参数J，P，I的变化规律可以看到，随着D2增大，非评估参数I有较为明显地增大，且递增幅度也大大地增高了，这代表着非关心部位的应力水平受D2的影响较为显著。此外，随着D2增大，评估参数J也有小幅度的增加，而评估参数I则小幅度减小，这表明D2对焊缝的应力均匀度及与倒角根部之间的应力差值的影响很小。根据综合评估参数C的值可以判断，当D2为3 mm的时候，结果是最优的。

图13 不同D2下评估参数对比

3.4 模拟件最终尺寸确定

经过优化分析之后，确定3个优化参量的尺寸，分别是D1为39.5 mm，D2为3 mm及ω为50°。表1给出了优化前后的模拟件各项参数的对比。通过4类评估参数的计算结果可以看出，虽然评估参数I和J的数值在优化后有微小的增加，但是根据评估参数P的变化可知，优化后大大降低了其他非关心部位的应力水平，从而降低了试验过程中模拟件疲劳破坏的位置出现在非焊缝区域的可能性。最后，由综合评估参数C的数值可以判定优化后的模拟件基本达到了优化目标的要求，提高了试验的成功率。

表1 评估参数计算结果

4 试验结果验证分析

采用MTS Biaxial平面双轴试验系统实现模拟件的双轴拉伸疲劳试验对可行性进行验证，试验条件为比例加载，加载频率为15 Hz，试验温度为室温，x轴和y轴加载应力比R均取0.1，采用16～40 kN的载荷级进行疲劳试验，试件的实物图如图14所示。

图14 模拟件实物图

根据疲劳试验结果，试件疲劳断裂位置随机出现在x轴或y轴的轴线焊缝处。该文以其中一件16 kN载荷下断裂位置在y轴轴线焊缝处的试件举例分析，图15为该试件的疲劳试验过程中裂纹萌生的示意图。该试件疲劳寿命范围为10 597～354 150循环次数，从图中可以看到试件疲劳裂纹萌生的位置在y轴轴线的焊缝处，并且沿着焊缝向两侧进行扩展。

从试件的最终断裂图（图16）可以看到，断口呈直线型平行于x轴，与模拟件设计的时候所预测的断裂位置相同。