磁性拓扑材料中贝利曲率驱动的非常规电输运行为*
2023-09-19杨金颖王彬彬刘恩克
杨金颖 王彬彬 刘恩克†
1) (中国科学院物理研究所,磁学国家重点实验室,北京 100190)
2) (中国科学院大学,北京 100049)
近年来,磁性拓扑材料特别是磁性Weyl 半金属越来越多地被发现,为研究拓扑输运行为提供了重要载体.磁性拓扑半金属材料具有动量空间的强贝利曲率,显著增强了电子的常规横向输运行为,也使得曾经被忽略或无法观测的输运效应逐渐浮现出来,导致当前广泛采用的经典输运方程不能准确地描述磁性拓扑电子的输运行为.本文从半经典输运方程出发,介绍磁性拓扑材料中新近出现的非常规电输运行为,内容涉及化学掺杂、磁场调制拓扑电子态、贝利曲率相关的线性正磁电阻及磁场线性依赖的输运行为.这些行为为磁性与拓扑相互作用下的电输运行为提供新的理解和思考.最后,对非常规电输运的发展进行总结和展望.
1 引言
磁性拓扑材料的出现使得越来越多奇异的物理效应在实验上被实现,包括量子反常霍尔效应[1,2]、大反常霍尔效应[3−5]、大反常能斯特效应[6,7]、自旋轨道极化子[8]等.2018 年,磁性Weyl 半金属Co3Sn2S2的发现首次实现了本征磁序和拓扑物理的耦合[3,9],为磁性体系中的拓扑物态和物理行为提供了优异的研究平台,迅速掀起了研究磁性Weyl 半金属的热潮[8,10−15].目前磁性Weyl 半金属Co3Sn2S2[3],PrAlGe[16],Co2MnGa/Al[4,5],EuB6[17]等均是典型的磁性拓扑材料.这类材料所具有的拓扑增强的贝利曲率,是内禀反常霍尔效应的物理根源,也是本文所论述的非常规电输运行为的起源.
内禀反常霍尔电导来源于占据态能带贝利曲率的积分[18],这意味着内禀反常霍尔电导能够反映k空间的贝利曲率,从而将宏观输运与内禀能带结构关联起来,而各类实验手段对能带结构的微观调制也能够通过测量反常霍尔电导的方式进行表征.近几年来,研究人员利用掺杂、磁场等实验手段对内禀能带结构进行了调制,并进行了电输运的测量.在磁性Weyl 半金属Co3Sn2S2中通过Ni 掺杂调制内禀能带结构,引起内禀反常霍尔电导增强[19];在磁性拓扑材料Co2MnAl 中通过改变磁场方向改变能带结构和贝利曲率的分布,从而调控内禀反常霍尔电导[5];当EuB6中磁场与易轴方向不平行时,出现磁矩倾斜,在磁矩未饱和时出现能带退简并,导致内禀贝利曲率变化和反常霍尔电导变化[17].
贝利曲率对常规的内禀横向电输运的决定性已深入人心.2022 年,一个基于半经典输运理论的研究将线性磁电阻与贝利曲率联系起来,提出了拓扑材料线性磁电阻的模型[20].该研究将贝利曲率引入纵向电输运中,同时使得纵向电输运也可以成为研究贝利曲率的一种方式.
在半经典输运方程中,贝利曲率不仅对内禀反常霍尔电导有贡献,也对我们熟知的纵向电导有一个 [1+(e/ℏ)B·Ω]-1的修正[20,21],这个重要的修正使得拓扑材料中可能出现线性磁电阻.此外,当材料体系存在倾斜的Weyl 锥时,电导正比于磁场一次方的项不为0,在纵向、横向输运中均有贡献[22,23].最近,在磁性Weyl 半金属Co3Sn2S2中观测到的奇对称磁电阻和霍尔电阻被认为是来源于这个贡献[24].磁性拓扑材料EuB6的输运研究表明,各向异性磁电阻(anisotropic magnetoresistance,AMR)和平面霍尔效应(planar Hall effect,PHE)中均存在着关于磁场奇对称的成分[25].
本文侧重介绍近年来在磁性拓扑材料中出现的非常规电输运行为,首先介绍半经典输运方程,随后以一些磁性拓扑材料体系为例介绍实验上的进展,如图1 和表1 所示.实验进展主要包含三部分,第一部分为内禀反常霍尔电导的调制,第二部分介绍贝利曲率对磁电阻带来的修正,最后介绍倾斜的Weyl 锥导致磁性Weyl 半金属的AMR 和PHE 中出现关于磁场奇对称的贡献.

表1 各类输运效应与材料体系对照表Table 1.Comparison of various transport effects and material systems.

图1 贝利曲率相关的非常规电输运行为Fig.1.The unconventional electric transport behaviors related to the Berry curvature.
2 贝利曲率与半经典输运方程
包含贝利曲率的半经典输运方程是理解非常规输运行为的重要基础,这里首先对贝利曲率进行阐述.1984 年,Berry 提出在绝热体系中,系统的哈密顿量在参数空间经历一个回路后,本征态会获得一个相位,这个相位被称为贝利相位.该相位可由贝利曲率的积分获得,贝利曲率的表达式为[26]
其中参数空间为k空间.贝利曲率的引入,将对磁性拓扑材料的电输运产生非常重要的影响.
基于半经典理论[21,22,27−30],电流表达式为
对比(3)式和(4)式,可以看到贝利曲率相当于动量空间的赝磁场,它是布洛赫电子在运动时所感受到的等效磁场.将(3)式与(4)式解耦,得到
假设电子在空间中均匀分布,根据玻尔兹曼方程,利用弛豫时间近似,可以得到电子非平衡分布函数:
式中第1 项为平衡分布函数,第2 项为电场导致的分布函数的偏离,第3 项表示磁场平行于电场时一对Weyl 锥之间存在电子转移,第4 项为高阶修正.将(5)式与(6)式代入(2)式即可得到电流密度表达式,仅保留电场的一次项,电场前的系数即为电导率.对(5)式的第2 项与(6)式的第1 项的乘积进行积分,即可得到内禀反常霍尔电导.我们熟知的纵向电导来源于(5)式第1 项与(6)式第2 项的乘积,其余各项将在本文其他部分进行讨论.
3 基于贝利曲率的横向电输运效应的调控
实空间内禀反常霍尔电导与k空间贝利曲率密切相关,而贝利曲率由电子能带结构决定.一切能够影响能带结构的因素都可能改变贝利曲率的分布,贝利曲率的变化能够通过实验测量的反常霍尔电导观测.通过掺杂调制材料内禀的电子能带结构,进而调制贝利曲率,在磁性Weyl 半金属Co3Sn2S2掺Ni 中得到了实现;外磁场方向对内禀贝利曲率分布的影响在磁性拓扑材料Co2MnAl和EuB6中被发现,并通过实验和理论计算共同证实了外磁场对拓扑电子态具有有效的调制作用.
3.1 化学掺杂调控拓扑能带结构
Co3Sn2S2是实验上第一个被证实的磁性Weyl半金属[3,9],费米能级附近的外尔点和节线环产生了大内禀贝利曲率.由于内禀反常霍尔电导与占据态的贝利曲率相关,想要调控内禀反常霍尔电导,需要从内禀的能带结构出发.同时,化学掺杂会在实验上产生反常霍尔电导的外禀贡献[31].最近,一项研究结果表明,在磁性外尔半金属Co3Sn2S2中引入少量杂质元素,可以对体系的拓扑能带产生调制,从而产生了显著的内禀反常霍尔增强[19].研究者采用Ni 元素对Co3Sn2S2进行掺杂[19],测量发现反常霍尔电导得到了显著提升.采用TYJ 模型对反常霍尔电导进行了内外禀成分分离,并结合第一性原理计算,发现掺Ni 后的反常霍尔电导增强主要来源于内禀贡献.如图2(d),(e)中反常霍尔电导σxy结果所示,计算和实验测量数据同时显示,随着掺杂量的增加,内禀反常霍尔电导出现反常的先增大后减小的行为,而非刚带模型所预期的一路下降,这说明杂质的引入改变了贝利曲率.如图2(a)—(d)所示,微量掺杂下理论计算的能带结构表明,随着掺杂量的增大,能带逐渐展宽,贝利曲率增强,内禀反常霍尔电导增大.这一工作从实验和理论计算上共同证实了掺杂会通过破坏晶体的平移对称性而对拓扑能带产生展宽调制效应,这为实验调控贝利曲率/反常霍尔电导提供了一个有效的方法.

图2 Co3−xNixSn2S2 的能带结构与内禀反常霍尔电导[19]Fig.2.The band structure and intrinsic anomalous Hall conductivity in Co3−xNixSn2S2[19].
3.2 磁场转动调控拓扑能带结构
磁矩的磁化方向会改变体系的对称性,对能带结构产生修正,因此反常霍尔电导对样品磁化方向有强烈的依赖关系.利用外磁场调控材料的磁化方向,研究其对内禀贝利曲率分布的影响,这一研究在磁性拓扑材料Co2MnAl 中得到了开展[5].如图3 所示,在磁场转动的过程中(图3(a)),贝利曲率的大小和方向均发生变化,最终反常霍尔电导与磁化方向形成类似cosθ形式的关系.图3(a)展示了随着角度θ的变化,反常霍尔电导的实验数值(红色空心圆环)、理论计算数值(黑色空心圆环)与cosθ曲线拟合(黑色实线)的结果,可以看到实验与理论计算结果一致,这个实验与理论计算直观地展示了随着外磁场角度的转动,贝利曲率发生演化,并表现出实验可观测的反常霍尔电导随磁场演化的整个过程.
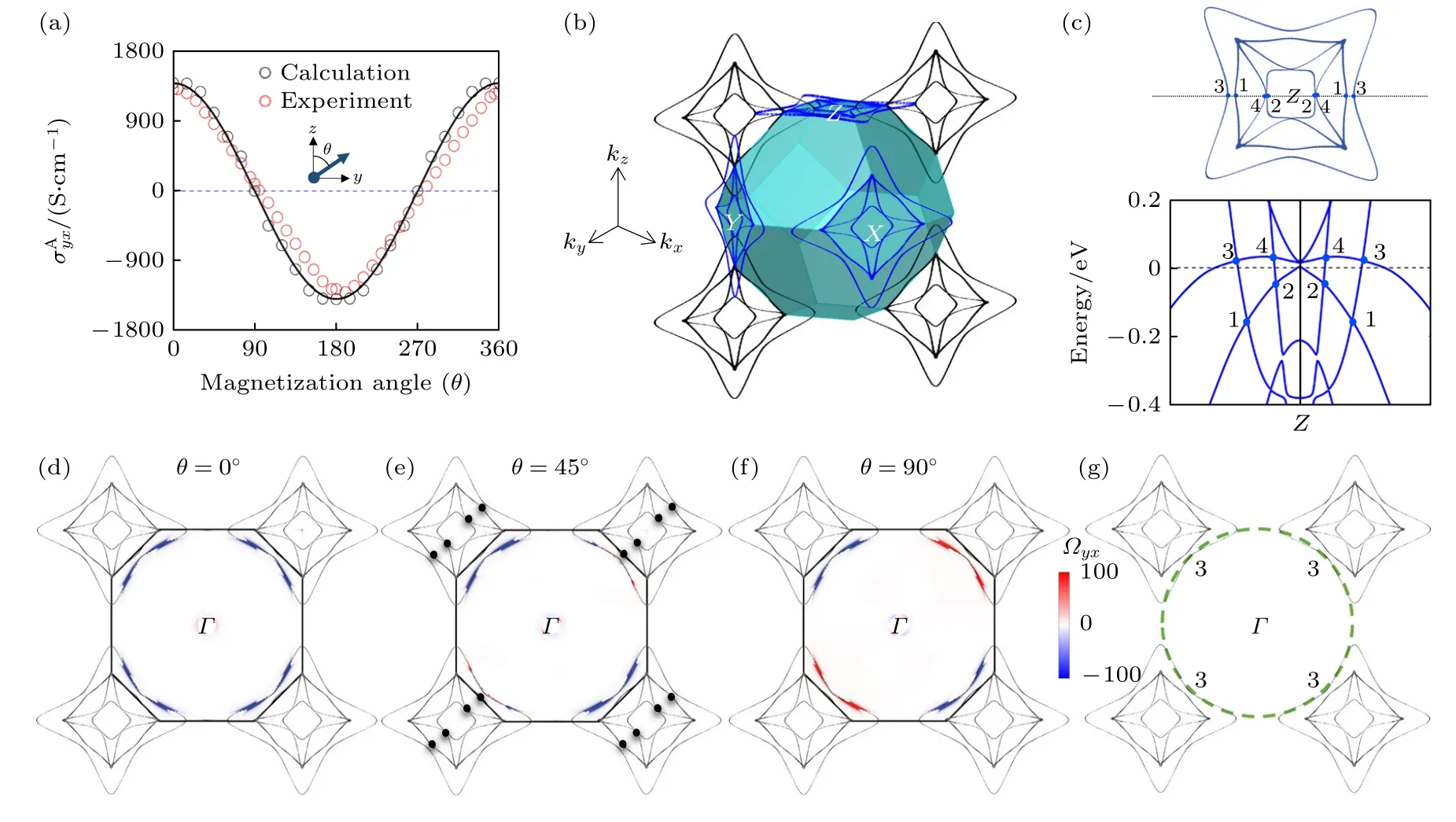
图3 Co2MnAl 中随着外磁场转动贝利曲率分布的演化[5]Fig.3.The evolution of Berry curvature distribution in Co2MnAl with the rotation of magnetic field[5].
3.3 外磁场诱导自旋倾斜态
2023 年,Shen 等[17]报道了稀土基磁性拓扑半金属EuB6的内禀能带调制效应.在其中,电输运测量、扫描隧道谱学技术和理论计算协同配合证实了磁矩方向对拓扑能带结构具有显著调制作用.关于EuB6和Co2MnAl 的两个研究内容均为磁矩取向对能带结构的影响,但二者采取了不同的实验路线,通过不同的方式改变磁矩方向来研究输运行为.在EuB6工作中,研究者采用磁晶各向异性能与外磁场下的塞曼能之间的竞争来研究磁矩在磁化转动过程中产生的自旋倾斜态对输运行为的影响;在Co2MnAl 工作中,所研究的对象是磁矩处于饱和态时的输运行为.这使得二者的测量配置不同: 对于Co2MnAl,通过改变磁场方向控制样品磁矩方向,所施加的电流方向和测量霍尔电压的方向不变;而对于EuB6(图4(a)),其易磁化轴沿[111]方向,通过外磁场使磁矩偏离易磁化轴,可获得自旋倾斜态.为了测量反常霍尔效应,采用了不同取向的单晶样品,所施加的电流与测量电压方向均改变.
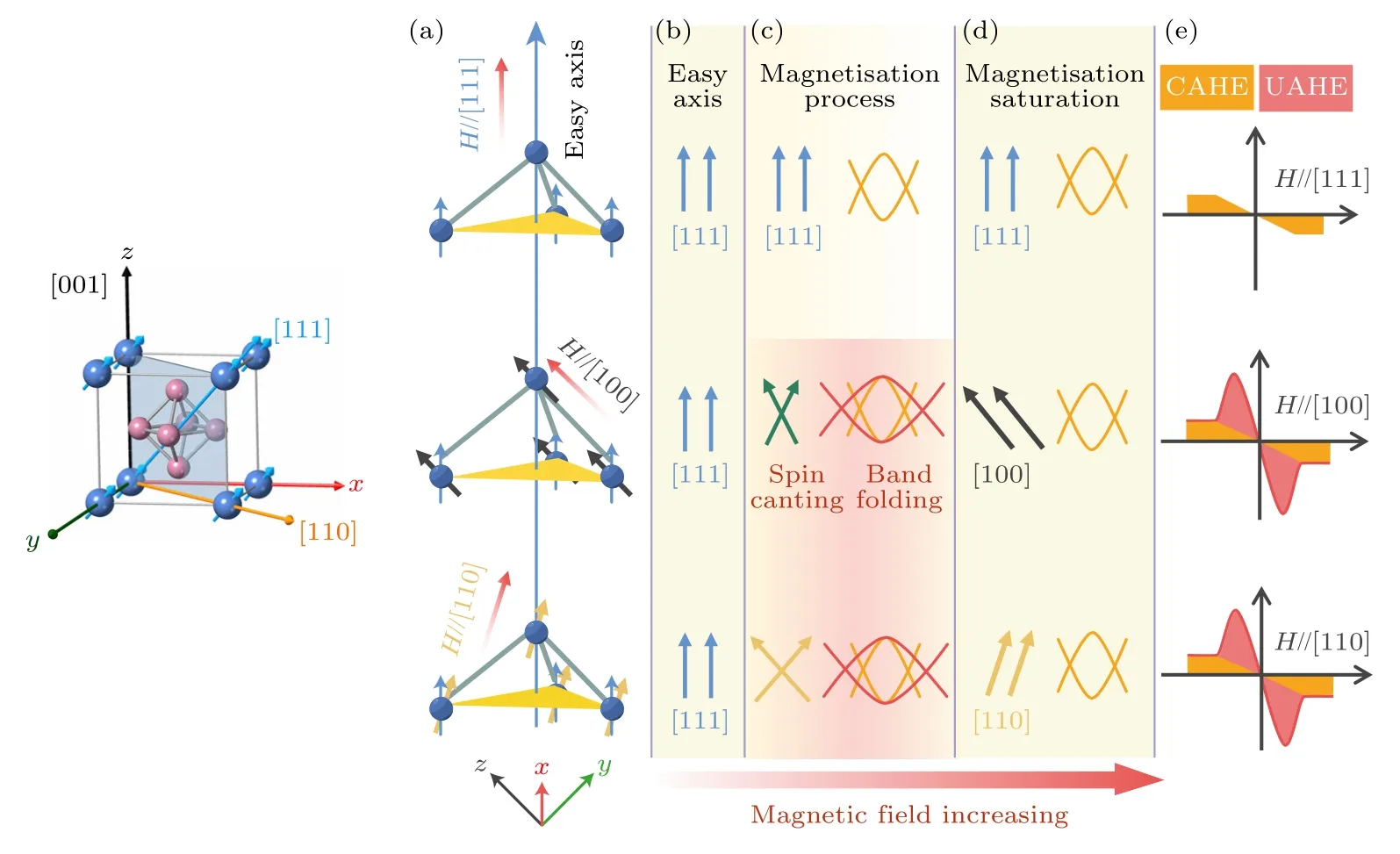
图4 EuB6 实空间磁矩方向、k 空间能带结构及输运行为演化示意图[17]Fig.4.Schematic diagram of the evolution of the real space magnetic moment direction,the k-space band structure and the transport behavior in EuB6[17].
EuB6中磁矩对能带及输运行为的影响如图4所示.当外磁场平行于易轴[111]方向时,反常霍尔电阻随着磁场增大单调增大,磁矩饱和后,反常霍尔电阻饱和.当外磁场偏离[111]方向,在磁矩饱和过程中,产生非共线的自旋倾斜,使得拓扑能带退简并,能带结构被调制,贝利曲率分布发生变化,磁矩饱和前反常霍尔电阻出现显著的极大值尖峰.磁矩饱和后尖峰反而消失,这一实验现象也证实了外磁场控制下的磁矩取向可以对内禀能带结构产生调制作用.
4 基于贝利曲率的线性正磁电阻纵向输运行为
2022 年,一篇研究磁性拓扑材料CoS2线性正磁电阻的工作被报道[20].该研究基于半经典的输运方程,将拓扑材料的线性磁电阻与k空间的贝利曲率联系起来.由于贝利曲率的引入,纵向电导积分项中出现了这一修正项[21].作者将费米能级处的贝利曲率取平均值后,得到

图5 CoS2 线性正磁电阻行为及含温度纵向横向输运实验数据拟合结果[20]Fig.5.The linear positive magnetoresistance behavior in CoS2 and experimental data fitting results of longitudinal and transverse with temperature[20].
其中Weyl 点的位置为(0,0,±c),Weyl 点和费米能级之间的距离为Δ,λ为外尔点处能带色散的斜率.利用(8)式和(9)式可以方便拟合实验数据,进而得到外尔相关的参数信息.此模型也可用于理解Dirac 体系在外磁场中所表现出来的磁电阻行为.该研究将纵向输运与贝利曲率关联起来,为拓扑材料中普遍存在的线性磁电阻提供了普适的理解.
5 基于贝利曲率的关于磁场反对称的面内输运行为
5.1 EuB6 的AMR 与PHE 研究
磁性拓扑材料的非常规输运行为不仅存在于磁场面外时的反常霍尔效应和磁电阻中,也存在于磁场面内时的PHE 和AMR 中.2022 年,一篇关于磁性拓扑半金属EuB6的工作报道了当Weyl 体系中Weyl 锥存在倾斜时,PHE 和AMR 中均存在关于磁场奇对称的项[25].而在拓扑平庸的材料体系中,AMR 和PHE 对磁场的依赖关系分别为cos2θ和 sinθcosθ,其中θ为磁场和电流的夹角.可以看到,AMR 和PHE 均关于磁场对称.在EuB6中出现的奇异奇对称行为也可以用半经典的方程进行讨论[22,23].
本文仅讨论磁场的一次方项,且仅考虑一对倾斜的Weyl 锥.Weyl 锥的倾斜方向在xy平面内时,存在3 项与磁场一次方相关的贡献.第1 项为(5)式中第3 项与电场带来的分布函数的变化相乘贡献的,第2 项为费米速度与手性化学势相乘贡献的,第3 项为D关于B·Ω展开的一次方项、费米速度和电场带来的分布函数的变化的乘积引起的的贡献.利用图6(a)中的角度关系,倾斜的Weyl 锥引起的关于磁场奇对称项的角度依赖关系为

图6 EuB6 中PHE 和AMR 中关于磁场奇对称输运行为[25]Fig.6.The antisymmetric transport behavior of PHE and AMR in EuB6[25].
这里仅对角度关系进行讨论.图6(b)和图6(c)中空心圆圈为实验测量的关于磁场奇对称的信号,实线为利用(10)式拟合的曲线,可以看到二者存在高度的一致性.倾斜Weyl 锥体系PHE 和AMR非常规行为的发现不仅将k空间的贝利曲率与更多输运现象联系起来,也使得PHE 和AMR 成为了一种研究磁性Weyl 体系的可选手段.
5.2 Co3Sn2S2 中磁场线性依赖输运行为
2021 年,在磁性Weyl 半金属Co3Sn2S2纵向和横向输运上也观测到了存在额外的奇对称贡献[24].这一工作与EuB6的PHE 与AMR 测量配置不同,EuB6的磁场方向是在面内旋转,而在Co3Sn2S2这个工作中磁场方向是从面外转至面内.随着磁场在面内分量越来越大,霍尔和磁电阻的信号中关于磁场奇对称项的贡献也越来越显著.与EuB6中的机制相同,体系中存在倾斜的Weyl 锥时,半经典输运方程中关于磁场的一次方项不为零,出现了纵向和横向输运的磁场线性依赖贡献.如图7 所示,磁场在xz平面及yz平面内时,观察到了因线性项导致的关于磁场反对称的霍尔电阻和纵向磁电阻.

图7 Co3Sn2S2 中关于磁场奇对称的纵向和横向电阻[24]Fig.7.The antisymmetric longitudinal and transverse electric resistivity in Co3Sn2S2[24].
Co3Sn2S2的研究在实验上观测到了关于磁场奇对称的输运行为,EuB6这个关于AMR 和PHE的输运研究详细推导并给出了横向和纵向电导与角度之间的关系,且在实验上进行了拟合,充分说明了当磁场在面内时,也存在与贝利曲率相关的电导贡献.大贝利曲率与拓扑能带结构密切相关,使得AMR 和PHE 也成为了一种研究拓扑电子能带结构的实验手段.
6 展望与结论
近年来,磁性拓扑材料的出现,使得源于贝利曲率的输运行为越来越引人注目.半经典的输运方程将实验可测的电导与k空间的贝利曲率联系起来,利用掺杂、磁场等手段,使得电输运成为了一种研究电子能带结构尤其是拓扑能带的一个手段.线性磁电阻是在磁场和贝利曲率共同作用下出现的一种现象,这一现象将纵向输运与贝利曲率联系了起来.与磁场一次方相关的PHE 和AMR 行为改变了人们对这两个效应的传统认知,也是磁性拓扑Weyl 半金属输运上的特征之一.由于本征磁性拓扑半金属材料近年来才出现,关于磁性拓扑材料中与贝利曲率密切相关的非常规输运行为还处于被陆续发现的过程中,但越来越多的研究结果表明,磁性拓扑材料电输运物理中潜藏着丰富的现象,未来会逐步被发现和研究.
