拓扑绝缘体中量子霍尔效应的研究进展*

张帅 宋凤麒

(南京大学物理学院,固体微结构物理国家重点实验室,人工微结构科学与技术协同创新中心,南京 210093)

三维拓扑绝缘体因其独特的物性备受研究人员关注,而拓扑表面态的输运是探索其新奇物性的重要手段.其中,拓扑表面态的量子霍尔效应则是拓扑绝缘体输运研究的一个重要内容.本文简要回顾了拓扑绝缘体中量子霍尔效应的实现与发展.比较了拓扑表面态量子霍尔效应与其他体系的差别,讨论了其材料体系的发展,并介绍了其中的标度律行为.之后详细回顾了实验上对拓扑表面态量子霍尔效应磁性近邻与栅压调控等方面的研究.最后,展望了拓扑绝缘体中量子霍尔态的研究前景,希望能促进拓扑绝缘体的应用.

1 引言

1980 年,Klitzing 等[1]在低温强磁场下测量金属氧化物半导体场效应晶体管(MOSFET)时,首次观测到量子霍尔效应(quantum Hall effect,QHE).这一没有自发对称性破缺的体系突破了朗道范式的框架.随后,Thouless 等[2]提出了著名的TKNN不变量来描述量子霍尔效应,也即陈数(Chern number).由此,拓扑量子物态的概念被引入到凝聚态物理的研究中.2004 年,Kane 和Mele[3,4]基于石墨烯的强自旋轨道耦合提出了具有量子自旋霍尔效应的二维拓扑绝缘体(topological insulator,TI).不久,Bernevig 等在HgCdTe 量子阱体系中也独立预言了量子自旋霍尔态[5],并成功在实验上观测到[6].随后,人们进一步将拓扑概念扩展到三维材料体系,发展并预言了三维拓扑绝缘体及其材料体系[7,8],且很快被实验证实[9].这些新奇的拓扑物态也是近年来凝聚态物理中重要的研究方向.

拓扑绝缘体材料因其新奇的物性而受到广泛的关注[10-13],并在未来的电子元器件方面具有独特的应用前景.三维拓扑绝缘体具有强自旋轨道耦合相互作用,并受时间反演对称性保护,其体相绝缘而表面态导电.其拓扑表面态(topological surface state,TSS)是二维的狄拉克电子体系,具有线性色散关系、非平庸Berry 相位和自旋动量锁定等性质,因而会产生诸多新奇的输运现象,如弱反局域化[14]、AB 振荡[15]、SdH 振荡[16]和普适电导涨落[17]等,这些输运行为可以反映出拓扑表面态的非平庸Berry相位和普适对称类等性质.其中,量子霍尔效应是拓扑表面态最重要的输运现象之一.

要在拓扑绝缘体材料中实现纯拓扑表面态的输运,其样品的品质是很重要的影响因素.对于三维拓扑绝缘体,早期其材料的拓扑表面态占比不高,过高的体相贡献使得量子霍尔效应难以实现.因此在Bi 基的三维拓扑绝缘体材料中,最开始是在四元体相绝缘的拓扑绝缘体BiSbTeSe2中实现完整的拓扑表面态量子霍尔效应.下面,对拓扑绝缘体表面态的量子霍尔效应实验进展作简要综述.

2 拓扑表面态量子霍尔效应的概述

在目前的量子霍尔效应中,根据所满足的方程,可以将其分为两类: 一类是由薛定谔方程描述的量子霍尔效应,如传统的硅金属氧化物半导体场效应晶体管和GaAs/AlGaAs 等材料的二维电子气体系;另一类则是由狄拉克方程描述的相对论型量子霍尔效应(relativistic QHE),其材料体系包含石墨烯和拓扑绝缘体等.这2 类量子霍尔效应在输运的表现上大体上是类似的,但在细节上有很多区别[18,19].

薛定谔方程描述的传统二维电子气体系在强磁场下形成的朗道能级为En=ℏωc(n+1/2),如图1(b)所示,其中ωc为回旋频率,ℏ为约化普朗克常数,n为被占据的朗道能级个数.可以看到,每个朗道能级间是等间距的,间隔为 ℏωc.当费米能处在朗道能级间隙中时,则表现出量子霍尔效应,量子霍尔电导平台为ν=n.因而这里都表现出整数化的量子霍尔电导平台,单位为e2/h,其中e为元电荷,h为普朗克常数.

图1 量子霍尔效应与朗道能级 (a) 量子霍尔效应的典型输运特征;(b) 传统二维电子气在磁场下的朗道能级示意图;(c) 二维狄拉克费米子体系在磁场下的朗道能级示意图;(d) 传统二维电子气量子霍尔手性边缘态示意图;(e) 拓扑绝缘体上下表面量子霍尔手性边缘态示意图.Fig.1.Quantum Hall effect and Landau levels: (a) Transport characteristics of quantum Hall effect;(b) Landau level diagram of conventional two-dimensional electron gas in magnetic field;(c) Landau level diagram of two-dimensional Dirac fermion system in magnetic field;(d) diagram of quantum Hall chiral edge states in conventional two-dimensional electron gas;(e) diagram of quantum Hall chiral edge states of top and bottom surface states in topological insulator.

而狄拉克方程由于考虑了相对论效应,其描述的费米子在磁场下其形成的朗道能级则为En=,如图1(c)所示.在固定的磁场下,朗道能级正比于,其每2 个相邻能级的间距是不相等的,且都会有所谓的零能模能级出现在狄拉克点处.其量子霍尔电导平台的值为ν=g(n+1/2),其中g为简并度,n对应被占满的最高朗道能级,是一个整数.这里多出的1/2 项也是狄拉克费米子区别于传统薛定谔费米子的最重要特征.对于单个狄拉克锥,其量子霍尔电导平台值是半整数的,因而又称为半整数量子霍尔效应(halfinteger QHE).但由于实际材料体系会受到Nielsen-Ninomiya 定理的限制[20],狄拉克锥总是成对出现,因此这里最终表现出的通常也是整数化的量子霍尔电导平台.比如,在石墨烯中由于自旋简并和谷(valley)简并的存在[21,22],其表现出四重简并度,即g=4,因此其量子霍尔平台值为ν=4(n+1/2).

在三维拓扑绝缘体中,单个二维的拓扑表面态是自旋极化的,其简并度被完全解除,即g=1,因此单个拓扑表面态的量子霍尔平台是一个半整数值,即ν=n+1/2.因为三维拓扑绝缘体中始终有上下2 个表面贡献量子霍尔态,且其自旋动量锁定的模式相反,所以实际得到的是整数化的量子霍尔平台,即ν=(ntop+1/2)+(nbottom+1/2)=ntop+nbottom+1.但其与传统二维电子气中的量子霍尔边缘态还是存在显著的区别,图1(d),(e)分别展示了2 种类型的手性边缘态示意图.在上、下拓扑表面态贡献相同的情况下,拓扑绝缘体中的量子霍尔态应则会呈现出ν=2n+1 的奇数化平台值.

本文主要讨论三维拓扑绝缘体中狄拉克电子的相对论型量子霍尔效应,以Bi 基三维拓扑绝缘体为主,来回顾和讨论拓扑绝缘体中的量子霍尔效应现象.

3 拓扑表面态量子霍尔效应的实现

3.1 拓扑绝缘体的材料优化

早期理论预言并被实验证实的具有单个狄拉克锥的三维拓扑绝缘体材料[23]是Bi 基的Bi2Se3,Bi2Te3和 Sb2Te3等,这类二元Bi 基拓扑绝缘体受自掺杂等效应的影响,具有较高的体相载流子浓度,其体相对输运总是会有不可避免的贡献,使得纯拓扑表面态的输运行为很难被直接观测到,从而令拓扑表面态的输运研究受到很大干扰.因此,优化拓扑绝缘体材料,实现体现绝缘的本征拓扑绝缘体材料就显得尤为重要,尤其是对拓扑表面态输运的研究.本征拓扑绝缘体材料需要满足2 个重要的要求: 一个是体相尽可能绝缘,体载流子浓度要小于1×1016cm-3;另一个是狄拉克点要落在体能隙内,如果狄拉克点落在导带或价带中,那么就难以实现对拓扑表面态的调控[24].

预言新的三维拓扑绝缘体材料是寻找高质量拓扑绝缘体的一种有效方式,而通过对现有拓扑绝缘体材料进行优化,能更迅速地实现本征拓扑绝缘体材料.这些不同二元Bi 基拓扑绝缘体会呈现出不同的n,p 型,且其构成元素Bi,Sb 和Se,Te 也分别属于同一族,因而通过补偿掺杂得到的四元拓扑绝缘体材料(Bi,Sb)2(Te,Se)3的体相会被极大抑制,在低温下可以实现拓扑表面态占主导的输运行为[25,26].这类本征Bi 基拓扑绝缘体材料为实现拓扑表面态的量子霍尔效应奠定了有效的材料基础.拓扑绝缘体材料的相关优化发展过程可以参看Heremans 等[24]综述文章.

3.2 拓扑表面态量子霍尔效应的实验观测

拓扑绝缘体中的量子霍尔效应最初是在HgTe中开展的.在应变的HgTe 体系中,实验上在高场下观测到了连续的整数量子霍尔平台,但其对应的纵向电阻却仍然很大,不满足无耗散的量子霍尔态要求.这可能是由于样品中存在体态、表面态和非手性的边缘态等的影响,从而使其出现了显著的耗散;而且其上、下表面由于受反演对称性破缺的影响,其朗道能级随磁场变化则会不再对准,从而出现了偶数的量子霍尔平台值[27].

普渡大学Xu 等[28]首先在BiSbTeSe2中观测到了完整的拓扑表面态量子霍尔效应(well-developed TSS QHE).在31 T 的磁场下,他们利用背栅调节下表面的费米能,即调节了对应的朗道能级指数nbottom,而此时上表面固定在1/2 态(ntop=0),于是实验上就观测到一系列整数间隔的量子霍尔平台,即ν=nbottom+1.他们观测到了很好的ν=-1,0,1,2,3 平台,并且ν=1,2 平台对应的纵向电导已基本接近于零,表明了其无耗散的特征.他们还通过背栅将下表面的载流子浓度调节到与上表面相匹配,此时磁场调控的量子霍尔态只有奇数化的量子霍尔平台值出现,即量子霍尔平台为ν=2(n+1/2),这与上下2 个拓扑表面态贡献相同的情况一致.

东京大学的Yoshimi 等[29]在分子束外延(molecular beam epitaxy,MBE)生长出的(Bi1-xSbx)2Te3薄膜中同样观测到了量子霍尔效应.他们通过测量不同x组分(x=0.84 和x=0.88)的样品,分别得到了不同的量子霍尔平台.对于x=0.84 的样品,14 T 磁场下可以观测到显著的ν=±1 量子霍尔平台,而ν=0 平台则很难分辨;对于x=0.88的样品,ν=1 和0 平台很显著,而ν=-1 平台则几乎看不到.这是因为在x=0.88 样品中,上下拓扑表面态狄拉克点的能量位置差异更大,因此其ν=0 平台就会明显的出现;而且,这两种组分的样品中狄拉克点都更接近于价带,而x=0.88 样品中无序的影响相对更大,所以其ν=-1 平台没有很好的形成.此外,在高质量(Bi0.53Sb0.47)2Te3薄膜中,也观测到了ν≤-2 的高阶量子霍尔平台[30].

除了这些多元的拓扑绝缘体,在二元的拓扑绝缘体中,Koirala 等[31]通过对生长方式的优化与改进,也实现了拓扑表面态的量子霍尔效应.他们首先在衬底上生长了In2Se3/(Bi0.5In0.5)2Se3异质结作为缓冲层,然后在上面用MBE 生长Bi2Se3薄膜,这样的界面工程可以显著减少界面和体的缺陷,从而得到高质量的样品材料.在这样的样品中,其迁移率能够高达16000 cm2/(V·s),并能观测到量子霍尔效应.这也是首次在二元Bi 基拓扑绝缘体中实现量子霍尔态.随后在界面工程的帮助下,他们通过Ca 掺杂Bi2Se3,得到了p 型Bi2Se3.虽然这里实现了量子霍尔态,但在该过程中,量子霍尔效应会随着载流子类型从n 到p 转变的过程中逐渐瓦解,并且会产生多余的导电通道[32].这也反映了其狄拉克点与价带间的能量间距小于其与导带的间距.随后,他们进一步利用该方式优化了纯二元Bi2Se3体系,实现了栅控的量子霍尔态[33].

随着拓扑绝缘体材料的进一步优化,人们发现通过少量的Sn 掺杂可以使得拓扑绝缘体的性质表现出更加优异的性质.Cava 等[34]首先生长出了体相高度绝缘的五元拓扑绝缘体材料Sn-Bi1.1Sb0.9Te2S,其块体电阻率可以超过100 Ω·cm,远远高于以往其他的拓扑绝缘体材料.Sn-Bi1.1Sb0.9Te2S 的体能隙约有350 meV,且狄拉克点完全处在体能隙中,距导带顶约230 meV,距价带顶约120 meV.这表明其狄拉克点更靠近价带,使得在输运测量中,n 型载流子区域的量子霍尔态更容易被观测到.在这种材料中,其体相更加绝缘,体载流子浓度小于3×1014cm-3,因而拓扑表面态的输运贡献占比更高.在介观尺度的五元Sn-Bi1.1Sb0.9Te2S 样品中,实验上观测到了其量子霍尔态,在6 K 的温度下,不到4 T 的磁场就可以使样品完全量子化到ν=1 平台,如图2(a)所示;且其样品的迁移率可以达到10000 cm2/(V·s)以上[35].随后,日本东北大学的Ichimura 等[36]在微米厚度和毫米平方面积的Sn0.02-Bi1.08Sb0.9Te2S 中,不施加栅压就观测到了其中的量子霍尔效应,如图2(b)所示.

将上述的拓扑绝缘体进行简单分类就可以发现,四元和五元的拓扑绝缘体都是通过布里奇曼等方式生长出块体材料,然后利用机械剥离得到的样品;而三元和二元的拓扑绝缘体则是通过外延生长的方法得到的拓扑绝缘体薄膜.这很可能是由于较厚的二元和三元拓扑绝缘体的体相贡献很大,需要精细的调控和较薄的厚度才能实现量子霍尔态;而四元和五元的样品体相较为绝缘,机械剥离的样品虽然相对较厚,但仍可以实现拓扑表面态占主导的输运行为.并且四元和五元的样品中更容易观测到高阶(ν＞1)的量子霍尔平台.从表1 中可以看出,介观的五元拓扑绝缘体样品实现量子霍尔态的条件更为宽裕.

表1 不同拓扑绝缘体中量子霍尔态的特征Table 1.Properties of quantum Hall state in topological insulators.

对于拓扑绝缘体,在厚度从几纳米到几微米之间的样品中,都可以很好地观测到量子霍尔效应,其厚度尺度可以跨越3 个数量级,如图2(b)所示.而且,不同于传统二维电子气需要很高的迁移率才能实现量子霍尔效应,这里的拓扑表面态能实现量子霍尔态的迁移率通常在几千cm2/(V·s)左右.这些都显示出了拓扑表面态的优越性.当然,对于更高质量的拓扑表面态,如Sn-Bi1.1Sb0.9Te2S 等,可以更深入研究其中丰富的物理效应.

4 拓扑表面态量子霍尔效应的标度行为

4.1 量子霍尔态的重整化群流标度关系

自从在BiSbTeSe2中实现拓扑表面态的量子霍尔效应之后,三维拓扑绝缘体中量子霍尔效应的丰富现象与物理特性就开始被进一步关注和研究.其中量子霍尔态的标度行为就是一个重要的方向.

重整化群流(renormalization group flow,RG flow)是描述量子霍尔态的有效手段.通过对复电导率σ=iσxx+σxy标度函数的分析,可以在复平面(σxy,σxx)上半部分给出其重整化群流的行为[37].理论上给出的重整化群流是周期性的,对于以往的整数量子霍尔效应,在σxy从0 到1 的一个周期内会存在2 个稳定固定点(stable fixed points),即(0,0)和(1,0).特别地,在一定条件下,除了稳定固定点外,该周期内还会存在一个不稳定固定点(1/2,1/2),这种情况下的重整化群流就呈现出一个半圆形的标度关系,如图3(a)所示.这种重整化群流的方式同样适用于分数量子霍尔效应[38]和量子反常霍尔效应[39]等其他量子霍尔态,只是其对应的稳定固定点会有所不同.

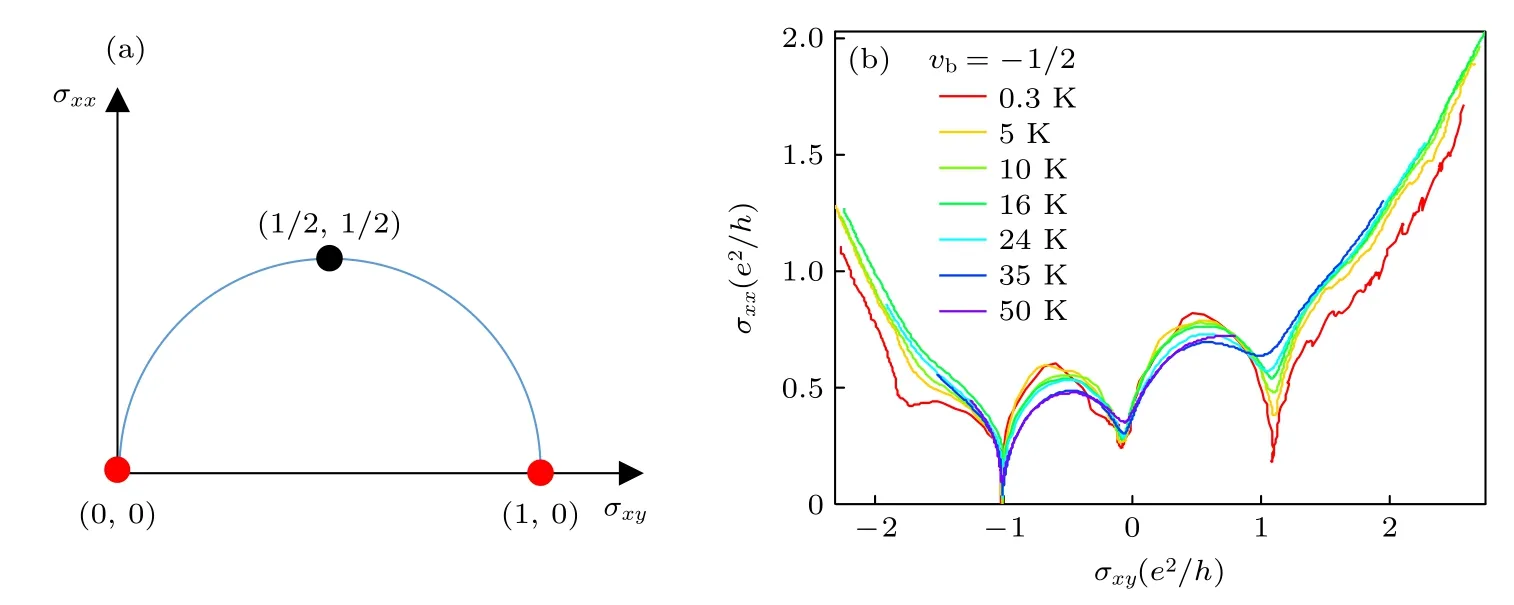
图3 量子霍尔态的重整化群流 (a)半圆形标度的重整化群流;(b)拓扑绝缘体中栅压驱动的重整化群流[40]Fig.3.Renormalization group flow of quantum Hall states: (a) Semi-circle renormalization group flow;(b) gate-driven renormalization group flow in a topological insulator[40].

对于本文拓扑表面态的量子霍尔效应,其同样适用.只是对于单个拓扑表面态,其一个周期内的稳定固定点为(-1/2,0)和(1/2,0).而由于2 个拓扑表面态的同时贡献,在不考虑2 个表面耦合的情况下,拓扑绝缘体中的重整化群流与以往整数量子霍尔效应是基本类似的.

实验上,通过调节温度、栅压和磁场等参数来实现电导复平面上的流.在其他参数不变的条件下,改变某一个调节参数,就可以得到复平面上的一条重整化群流线,这条线在这个参数调节下会流向稳定的固定点.图3(b)给出了下表面固定在-1/2 态时,顶栅驱动的重整化群流,其依次流向(-1,0),(0,0)和(1,0) 这3 个固定点(流向与扫栅压的方向相关)[40].而温度驱动[29]和磁场驱动的重整化群流[43],其也都会分别流向量子化的固定点.并且,这里3 种方式驱动的重整化群流都符合半圆形的标度关系.

4.2 量子霍尔平台转变的标度关系

拓扑绝缘体中量子霍尔态的耗散行为是一个重要的输运特征.实验上在高质量的五元Sn-Bi1.1Sb0.9Te2S中探索了其温度引起的耗散演变.在这种高质量的量子霍尔态中,当温度低于20 K 时,量子霍尔态的耗散行为满足变程跳跃方程的描述;而当温度高于20 K 时,其耗散则转变为热激发的行为[35].

进一步地,量子霍尔平台转变的标度行为也被实验揭示了.量子霍尔平台转变(quantum Hall plateau-to-plateau transition)是一种连续相变行为,当其在相邻两个量子霍尔平台间变化时,就会经历从量子霍尔绝缘态到金属态再到量子霍尔绝缘态的转变,如图1(a)所示,这就可以探索其中的标度关系[41,42].在低耗散的变程跳跃区内,得到了一个磁场驱动的量子霍尔平台的转变,即量子霍尔态随着磁场的增大从ν=2 平台转变到ν=1 平台,如图4(a)所示.这个相变行为随温度的变化满足公式(dRxy/dB)max∝T-κ和ΔB-1∝T-κ,其中ΔB为相变区域纵向电阻的半高宽,而指数κ通常为常数值.这里实验拟合得到的临界指数κ≈0.2,如图4(b)所示[35].而在传统二维电子气中临界指数通常为0.42;这里的临界指数约为传统二维电子气中的一半.这是因为拓扑表面态中的相互作用机制与二维电子气不同,反映了不同于非拓扑态中的起源.

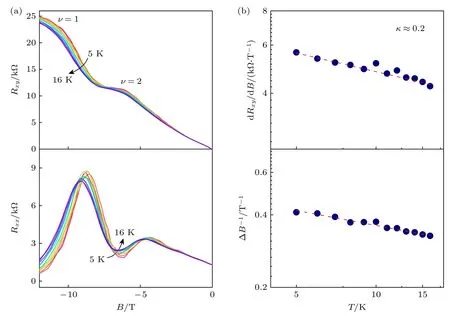
图4 拓扑绝缘体量子霍尔态的标度律行为[35] (a)量子霍尔平台在不同温度下的转变,上图为霍尔电阻的转变,下图为纵向电阻的转变;(b)量子霍尔平台转变中的标度律,上图为dRxy/dB 随温度的关系,下图为ΔB 随温度的关系Fig.4.Scaling law of quantum Hall states in topological insulators[35]: (a) Quantum Hall plateaus transition,Hall resistance (upper)and longitudinal resistance (lower);(b) scaling law in plateau transition region,relationship between dRxy/dB and temperature (upper) and relationship between ΔB and temperature (lower).

之后,在利用界面工程生长出的低载流子浓度的Ti 掺杂的Sb2Te3薄膜中,也得到了相同的标度行为.该样品的载流子浓度低至1011cm-2,这避免了样品中电子空穴水坑(electron-hole puddles)的影响.当施加足够的磁场使其达到量子极限后,在零朗道能级处就会观测到一个量子霍尔态到绝缘态的转变(quantum Hall to insulator transition),该相变由ρxx(B,T)∝|B-Bc|T-κ来描述.通过对该相变的标度律分析,得到的临界指数同样为κ=0.2[43].

这两个工作这意味着,量子霍尔平台的转变和量子霍尔态到绝缘态的相变都具有普适的标度行为.

5 拓扑绝缘体中量子霍尔效应的调控

5.1 拓扑表面态的磁性修饰与近邻

拓扑表面态可以被磁性等材料近邻,从而诱导出生新奇的量子效应,如量子反常霍尔效应[44],这也是研究磁性近邻效应的主要目的.然而实验上却遭遇到了很多困难,直到2019 年,才有实验报道了磁性近邻下的量子反常霍尔效应[45].这里主要介绍磁性近邻对拓扑表面态量子霍尔态的影响.

Yoshimi 等[46]制备了拓扑绝缘体的半磁性双层结构,即Crx(Bi1-ySby)2-xTe3和(Bi1-ySby)2Te3构成的双层异质结.在这种结构中,在一定的磁场下就可以实现0 和1 这2 个量子霍尔平台,其来源于表面态朗道能级和表面态磁能隙的贡献,其中磁能隙的贡献与量子反常霍尔态相关.而且,这里量子化的温度可以达到2 K,意味着半磁性结构中具有近邻效应,同时也抑制了表面态输运中无序的影响.

磁性团簇的修饰也会影响拓扑表面态的量子霍尔效应,利用磁性的钴团簇修饰BiSbTeSe2的上表面,实现了反常的输运现象[47].修饰后的拓扑绝缘体在足够强的磁场下仍表现出整数化的量子霍尔态;但相比于修饰前的样品,其量子霍尔态的剩余纵向电阻明显变大,这说明团簇修饰会引起一定的无序和散射,导致其中输运的耗散增加.而在中等磁场下,磁性团簇修饰后的拓扑表面态输运在重整化群流下展现出反常的量子化轨迹,如图5(a),(b)所示.这是因为,磁性团簇与上表面具有反铁磁交换耦合,从而打开塞曼能隙,使得零朗道能级偏移到塞曼能隙的顶端,增大了零朗道能级与-1 朗道能级的间距,因此推迟了上表面朗道能级的杂化.在这一过程中,干净的下表面始终保持在-1/2 的量子化,而修饰后的上表面则会从非量子化的-e2/h连续变化到0,所以会出现一个类半整数的-3/2 量子霍尔平台.

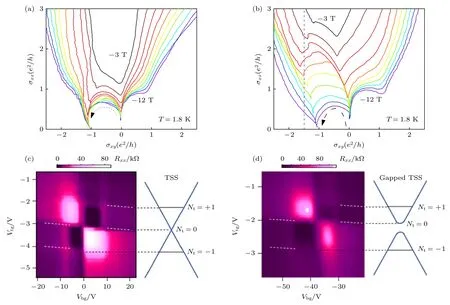
图5 磁性修饰与近邻下的量子霍尔态.磁性团簇修饰前(a)和磁性团簇修饰后(b)的量子霍尔态的重整化群流[47];h-BN 作为介电层(c)和Cr2Ge2Te6 作为介电层(d)的量子霍尔态[48]Fig.5.Quantum Hall states tuned by magnetic modification and proximity.Renormalization group flow of quantum Hall States before (a) and after (b) magnetic cluster modification[47];quantum Hall states with h-BN as the dielectric layer (c) and Cr2Ge2Te6 as the dielectric layer (d)[48].

随后,在二维铁磁绝缘体Cr2Ge2Te6与拓扑绝缘体BiSbTeSe2制备异质结中也观测到了相似的现象.Cr2Ge2Te6既可以充当介电层来调节BiSbTeSe2的费米能,其铁磁性还可以近邻拓扑表面态.在这样的异质结中,拓扑表面态被打开能隙,且可以访问表面态不同的费米面位置,从而实验上也测量到了一个类半整数的量子化霍尔平台[48],如图5(c),(d)所示.

最近,在半磁性拓扑绝缘体结构的基础上,实验上在零场下观测到了磁能隙贡献的单个表面态半整数化的量子霍尔平台[49].

5.2 双栅调控的量子霍尔态

拓扑绝缘体的上下2 个表面态会因厚度的不同而具有不同的耦合现象.无论上下2 个拓扑表面态是否耦合,都可以通过顶栅和背栅共同调节,实现双栅(dual gate)调控,从而探索其中更多的物理效应.通常双栅的器件结构是将薄层的六方氮化硼(h-BN)在覆盖在拓扑绝缘体介观样品上表面作为介电层,来施加顶栅;结合二氧化硅的背栅,就可以得到双栅压调控的器件.

对于厚度在100 nm 左右的BiSbTeSe2样品,这里2 个栅压可以独立调控上下2 个表面态,从而得到一系列上下表面不同半整数填充因子的组合态,如图6(b)所示.当上下表面的填充因子分别为(-1/2,1/2)或(1/2,-1/2)时,就会出现零霍尔平台,并伴随纵向电阻出现一个巨大的峰值,这是由耗散的非手性的边缘态导致的.通过非局域(nonlocal)测量与传统四端法测量的比较,揭示了标准量子霍尔平台和零霍尔平台的输运本质,证明了零平台的耗散边态不依赖于温度,说明了这里耗散边缘通道上的输运可能不存在标准的局域化行为[40].

图6 拓扑表面态量子霍尔效应的双栅调控 (a)—(c)随厚度减小,量子霍尔态在双栅调控下的不同行为[40,50,51]Fig.6.Dual-gate-tuned quantum Hall states of topological surface states: (a)-(c) different behavior of quantum Hall states with decreasing thickness[40,50,51].

而在更厚的样品中,上下拓扑表面态载流子类型不同情况下的双栅调控则会得到非整数的量子化平台.对于约240 nm 厚的BiSbTeSe2样品,利用双栅分别调控上下拓扑表面态,将2 个表面分别调到电子和空穴态,这样上下表面的量子霍尔边态在同一边缘处是反向的,而自旋方向相同.在这样厚度的样品中,实验上观测到了一系列非整数的量子霍尔平台值.这是因为,反向传播的边缘通道与上下表面态相反的螺旋相结合,使得这2 个边态之间存在相互作用;当相互作用强时,霍尔平台表现出预期的整数值;而当相互作用较弱时,就会出现非整数的霍尔平台,如图6(a)所示.正是由于样品较厚,相互作用弱,所以得到了非整数的平台.这种相互作用可以从电极中化学势的平衡和上下表面边缘模之间的散射来理解,且可以通过Landauer-Büttiker 公式来模拟这些平台值[50].

当样品厚度变得更薄后,双栅调控会给出新奇的输运现象[51].通过对不同厚度BiSbTeSe2样品的双栅调控研究发现,随着样品厚度的减小,上下表面间的耦合增强.当样品厚度≤16 nm 时,2 个表面会强烈的耦合在一起,使得量子霍尔平台间的转变会变成非线性;而且电中性点处的零朗道能级会发生劈裂,如图6(c)所示.此外,这还估算出了BiSbTeSe2的介电常数ε平均约为28.

以上所述的为垂直栅控结构,即上下2 个表面各施加一个全局的栅压,探索2 个表面不同耦合情况的行为.此外,还可以通过在一个表面部分施加栅压来构造出平面内的p-n 结,实现对其输运行为的调控,探索其中手性边缘态的透射与反射行为.

在同元素不同比例的四元拓扑绝缘体BiSb Te1.25Se1.75中,同样观测到了拓扑表面态的量子霍尔效应[52].通过局域顶栅的构型构造出平面内栅压,就可以在拓扑表面态实现得到n-p-n 结的结构.在这样的结构中,其量子霍尔边缘态在n-p 和p-n 结边界的手性不同,从而会在电输运上引起抑制或增强的现象;并观测到了一系列分数化的量子平台,且平台值可以通过手性边缘态的网格传输的Landauer-Büttiker 公式来模拟出.

5.3 量子霍尔态的光调控与量子电容

光照也可以调控Sn-Bi1.1Sb0.9Te2S 拓扑表面态的量子霍尔效应.相比于黑暗状态,11 μW 光照下的量子霍尔平台对应的栅压会往负方向偏移,且量子霍尔平台宽度也会展宽.这表明光照对拓扑表面态输运展现出明显的电子掺杂效应,且光照下体相对输运仍然没有贡献[53].这是拓扑表面态和窄带隙体相协同响应的行为,对进一步研究光控的量子霍尔态具有一定意义.

通过量子电容(quantum capacitance)的测量,可以深入研究拓扑表面态的朗道能级[54].之前实验上通过热激发拟合得到的能隙比理论值小近1 个数量级,这是因为没有考虑量子电容对态密度的影响.利用电容的测量,实验上测得了BiSbTeSe2样品(厚度约17 nm)最低的朗道能级的间距在18 T 磁场下约为40 meV,这与理论值一致.随后的电容谱实验进一步研究了BiSbTeSe2中的量子电容和态密度的行为,发现在这类补偿掺杂的拓扑绝缘体中,绝缘的体相提供了一个可以吸收大量电荷载流子的载体[55];这也解释了以往实验中栅压的调节效率为何会远小于理论值.

6 总结与展望

本文简单回顾了拓扑绝缘体中量子霍尔效应的研究进展,介绍了拓扑表面态量子霍尔效应的特点及其在实验上的观测,讨论了其中的标度律关系,并重点介绍了实验上对拓扑表面态量子霍尔效应的调控.目前这个方向的研究已经取得了诸多重要进展,但该领域仍有很多相关工作亟待展开.

首先,是更高质量的量子霍尔态.目前,拓扑绝缘体已经具备了高质量的材料体系,可以实现纯表面态输运占主导.但到现在,能实现拓扑表面态量子霍尔效应的温度大概只能达到50 K.虽然这个温度相对而言已经不低,但能否像石墨烯一样在室温下实现拓扑表面态的量子霍尔效应[56],或是进一步提高其量子霍尔态的温度,仍是一个值得思考和努力的方向.这或许需要更高质量的拓扑绝缘体材料体系.比如可以通过优化材料的生长和加工方式,降低材料体系中的缺陷和无序等,从而提高的拓扑表面态迁移率;理论上可以寻找预言具有更大的体能隙的新拓扑绝缘体材料等.而更高质量的拓扑绝缘体材料,也有望能使得其量子霍尔态的起始磁场进一步降低.

其次,是基于量子霍尔态的新奇现象.三维拓扑绝缘体中的零平台已经被观测到,其绝缘的性质也已被研究了.而理论上提出,基于其零平台可以实现拓扑磁电效应(topological magnetoelectric effect)[57]和独特的自旋输运[58]等.而且,通过厚度等方式对上下拓扑表面态的耦合进行调控,还有望探索拓扑激子凝聚(topological exciton condensates)等效应[59].

最后,是对拓扑表面态量子霍尔态的调控与应用.量子霍尔效应的手性边缘态是实现量子霍尔干涉仪的有效体系.理论上预言,在p-n 结构型的拓扑绝缘体中,当其进入量子霍尔态后,可以实现一种新奇的基于自旋的马赫增德尔干涉仪(spin-based Mach-Zehnder interferometry),其能够通过面内的磁通来调节其干涉效应[60].这种自旋的马赫增德尔干涉仪与传统的电子干涉仪不同,可以用作新型的自旋过滤器;且该构型可以很好地研究拓扑绝缘体中的自旋动量锁定效应.而当拓扑绝缘体中的量子霍尔效应被进一步与优化后,还可以探索超导近邻对拓扑表面态量子霍尔效应的影响,比如基于量子霍尔的超导干涉仪[61],甚至马约拉纳态[62]等.

随着对拓扑绝缘体中量子霍尔效应研究的深入,将会推进对拓扑绝缘体的认识,并提供其在电子元器件方面的应用基础.比如利用电场调控将材料从拓扑绝缘态(“开”)切换到传统绝缘体(“关”),从而实现拓扑态开关的拓扑晶体管[63].我们期待在这一领域看到不断的进展与突破.