狄拉克量子材料中的输运理论进展*
2023-09-19王焕文付博沈顺清
王焕文 付博 沈顺清
1) (电子科技大学物理学院,成都 611731)
2) (香港大学物理学系,香港 999077)
狄拉克量子材料具有独特的电子结构,可以用无质量和有质量的狄拉克方程描述.从奇异的量子流体到晶体材料的多种系统均已发现了狄拉克量子材料.由于其拓扑非平庸的能带结构,狄拉克量子材料表现出丰富有趣的输运现象,包括纵向负磁阻、量子干涉效应和螺旋磁效应等.本文介绍狄拉克量子材料输运理论最新进展,总结了基于狄拉克方程的相关量子输运理论和量子反常效应,重点关注有质量的狄拉克费米子和量子反常半金属,介绍了半磁拓扑绝缘体中宇称反常和半整数量子霍尔效应的实现.
1 引言
随着科学技术的快速发展,人们对新型拓扑材料和相关物理现象的研究愈发深入.狄拉克量子材料具有独特的电子结构,其低能激发可由狄拉克方程描述[1,2],从奇异的量子流体到晶体材料,狄拉克量子材料已经在各种系统中被发现,例如:3He-A相[3]、石墨烯[4−6]、拓扑绝缘体[1,7−10]、过渡金属二硫族化合物[11,12]、拓扑晶体绝缘体[13,14]及三维狄拉克和外尔半金属[15,16]等.同时,狄拉克量子材料的研究为拓扑量子计算提供了可能,开启了全新的物理领域,为实现丰富的拓扑相提供了新的平台,如各种新奇的量子霍尔效应和拓扑超导相[17−20],它们也是将来实现拓扑量子计算最有希望的材料.另一方面,狄拉克材料的出现促进了拓扑能带理论的发展[21].此外,由于非平庸的能带结构,狄拉克量子材料表现出一系列丰富有趣的输运现象[22−27],如负磁阻效应[28−50]、量子干涉效应[51−76]、霍尔效应[77−110]等.目前狄拉克量子材料中的很多输运现象在理论上还未被很好地理解,如弱场下的线性磁阻效应[111−119]、反常霍尔效应[92−97]和三维量子霍尔效应[85,86,120]等.对这些输运性质的研究有助于加深对狄拉克量子材料性质的进一步了解,对其未来在自旋电子学和量子计算等领域的应用具有重要指导意义.本文基于狄拉克方程,总结和回顾了其中的量子输运理论和量子反常效应等[48−50,72,75,121],并对我们最近提出的量子反常半金属的输运特性进行了初步综述[122−125].本文的结构安排如下:1)相关理论模型介绍,包括有质量的狄拉克方程和量子反常半金属的能带结构;2)总结有质量狄拉克费米子的负磁阻效应的相关理论;3)介绍二维和三维体系中量子干涉效应引起的磁阻效应,并应用至相关实验体系;4)讨论狄拉克费米子中的量子反常效应和螺旋磁效应,探讨了手性反常和螺旋对称性破缺的联系和区别;5)最后,详细介绍了最近发现的量子反常半金属的奇特输运性质,包括半整数量子霍尔电导和1/4 的拓扑磁电效应;6)给出评论和展望.
2 理论模型
2.1 狄拉克方程
有质量的狄拉克方程具有如下形式[1]:
其中γ0=τ1σ0和γj=-iτ2σj(j=x,y,z) 是伽马矩阵,σ和τ是泡利矩阵,v是有效速度,mυ2是狄拉克质量,ℏkj是沿着j方向的动量.在m=0 时,H0和手性算子γ5=iγ0γ1γ2γ3=τ3σ0对易,因而无质量的狄拉克费米子具有手性对称性,但是对有质量的情况,[γ5,γ0]=-2imυ2τ2=0,手性对称性被狄拉克质量破坏.不过此时H0还具有螺旋对称性,这里螺旋度χ=±被定义为k·σ|k,χ〉=χk|k,χ〉,其中,cosθχ=χkz/k以及 tanϕk=kx/ky.利用螺旋度的本征态,可以得到H0的本征能量和本征波函数为[50]
其中 cosϕχ=χυℏk/εkζ.ζ=+1 代表导带,ζ=-1代表价带.
在有限磁场下,ℏkj被替换为运动学动量(kinematical momentum)Πj=ℏkj+eAj,这里假设磁场沿着z方向,并选取相应的规范场为A=(-By,0,0).因为A并没有破坏x和z方向的动量,因此kx和kz依然是好量子数.Σ·Π=τ0σ·Π定义了粒子沿着运动方向自旋的投影.在有限磁场下,通过引入升降算符和a†=[126],得到体系的朗道能级的能谱和本征态[50]:
值得注意的是,模型(1)不包含能带拓扑的信息,为了进一步探讨能带拓扑对输运性质的影响,需要引入动量依赖的狄拉克方程,即修正的狄拉克方程[1,3]:
当mb>0 时,N=±1 对应了拓扑非平庸的能带结构.而mb<0 则对应了N=0 拓扑平庸的能带结构.此外,当m=0,b=0 时,模型(6)于半金属态,属于我们最近提出来的量子反常半金属[122].
2.2 量子反常半金属
自量子霍尔效应出现以后,拓扑物态和拓扑材料已逐渐成为凝聚态物理中最前沿的课题之一.截至目前,所有拓扑物态,包括量子霍尔效应[129,130]、拓扑绝缘体[7−9]、拓扑超导[8,131]和拓扑半金属[15,16,132]等都是以整数的拓扑不变量去表征.在文献[122]中,我们提出了量子反常半金属(quantum anomalous semimetal,QAS)的概念,并讨论了其中新奇的物理现象.这里以d维的无质量的Wilson 费米子为例进行介绍[133,134]:
其中a是晶格常数,αi和β是狄拉克矩阵.Wilson费米子的能带
在ki=0 时闭合形成单个无质量的狄拉克锥.在d=1,3 时,b项破坏了手性对称性;而在d=2 时,b项破坏了宇称对称性,这些对称性在k→0 的时候得以恢复.不同于以往有能隙的拓扑物态,k→0附近的手性对称性或宇称对称性保证了反常量子半金属的半整数拓扑[122].
当d是奇数时,存在某个矩阵Γ与(8)式反称,即{Γ,H}=0,Q矩阵可以被变换为非对角形式. 这里讨论d=1,3 的 情况,其对应的缠绕数可以写成[131]
其中εnst是Levi-Civita 符号,n,s,t=x,y,z.对于一般的体系,在k→0 附近具有手性对称性时,w1D和w3D是半整数量子化的.对于一维和三维Wilson费米子,Γ分别为σ2和γ1γ2γ3,由(9)式和(10)式给出的缠绕数为
当d=2 时,陈数可以表示为非阿贝尔的贝里规范场,
其中A是贝里规范场.对于有能隙的体系,ν2D始终是整数,而对于二维Wilson 费米子,ν2D=是半整数量子化.
文献[122]对于QAS 的半整数拓扑不变量进行了更加普适的证明,只要在狄拉克点附近具有手性(奇数维)或宇称(偶数维)对称性,缠绕数或陈数就是半整数量子化的.在物理上,半整数的拓扑不变量将使得QAS 具有一系列奇特的性质.对于一维的情形,QAS 可以实现半个电荷的转移,而在有能隙体系当中只能实现整数个电荷的转移.对于二维的情形,QAS 不具有边缘态,但可以给出幂律衰减的手性流(chiral current)和半整数化的霍尔电导[123,124].而在三维体系,QAS 则具有1/4 量子化的磁电响应[125].
3 有质量狄拉克费米子的负磁阻性质
负磁阻已经在很多外尔和狄拉克半金属中被观察到,其物理起源和手性反常(chiral anomaly)紧密联系在一起[42,43].然后负磁阻也在很多有质量的体系中被探测到[28−40],例如ZrTe5[34,40]和Bi2Se3[36,37,39],其中ZrTe5具有一个随温度变化的小的能隙[85,121,135],Bi2Se3则是典型的拓扑绝缘体[136,137].在这些体系中手性已经不再是一个好量子数[138],因而手性反常引起负磁阻的说法也受到了质疑,许多和手性反常无关的机制在文献中被提出[44−50],例如能带的非平庸贝里曲率和塞曼效应引起的贝里曲率和轨道磁矩等[45,46].在文献[48−50]中,我们提出了几个新的关于弱场负磁阻的物理机制.首先基于Kubo-Streda 公式计算了有限磁场下三维有质量狄拉克费米子中的电导张量σ,并进一步计算得到了电阻张量ρ=σ-1[48].在半经典区域,利用特殊函数对朗道能级求和,我们发现横向电阻和纵向电阻在磁场下均具有一个磁场强度平方的修正,其相对磁阻具有如下形式:
当λγ→0 的时候,有cx=cy=1,cz=-1/4 .此时,相对磁阻δραα(B)仅由费米波矢kF决定,而和能隙以及无序无关,我们将所得到的磁阻命名为内禀磁阻.在文献[45]中,通过考虑无质量狄拉克费米子的阿贝尔贝里曲率,半经典理论也得到了类似的内禀磁阻.对于有质量狄拉克费米子体系,体系具有非阿贝尔贝里曲率,非阿贝尔的规范场可以为计算得到的内禀磁阻提供一个可能的物理图像.值得注意的是,cz<0,纵向内禀磁阻是负磁阻.而这里的计算并未考虑不同手性的粒子之间的散射,内禀磁阻是完全不同于手性反常引起的负磁阻机制.与此同时,随着散射增强,这里的内禀效应将会被抑制住.图1(b)计算了不同狄拉克质量下(mυ2/υℏkF=0,1,2)cα关于λγ的函数关系,当λγ>0.1 时,cα随着无序增强而迅速减小.由于BF正比于载流子浓度的2/3 次方,实验中,我们期待在一些低载流子浓度的材料中观测到这里的内禀磁阻.此外,在(13)式中cx=cz,这反映了狄拉克费米子的各向异性磁阻性质,也将进一步导致平面霍尔效应,其中σ0是零场电导,φ是磁场和电流之间的夹角.近年来各向异性磁阻和平面霍尔效应在狄拉克材料中引起了广泛报道和讨论[98−107].
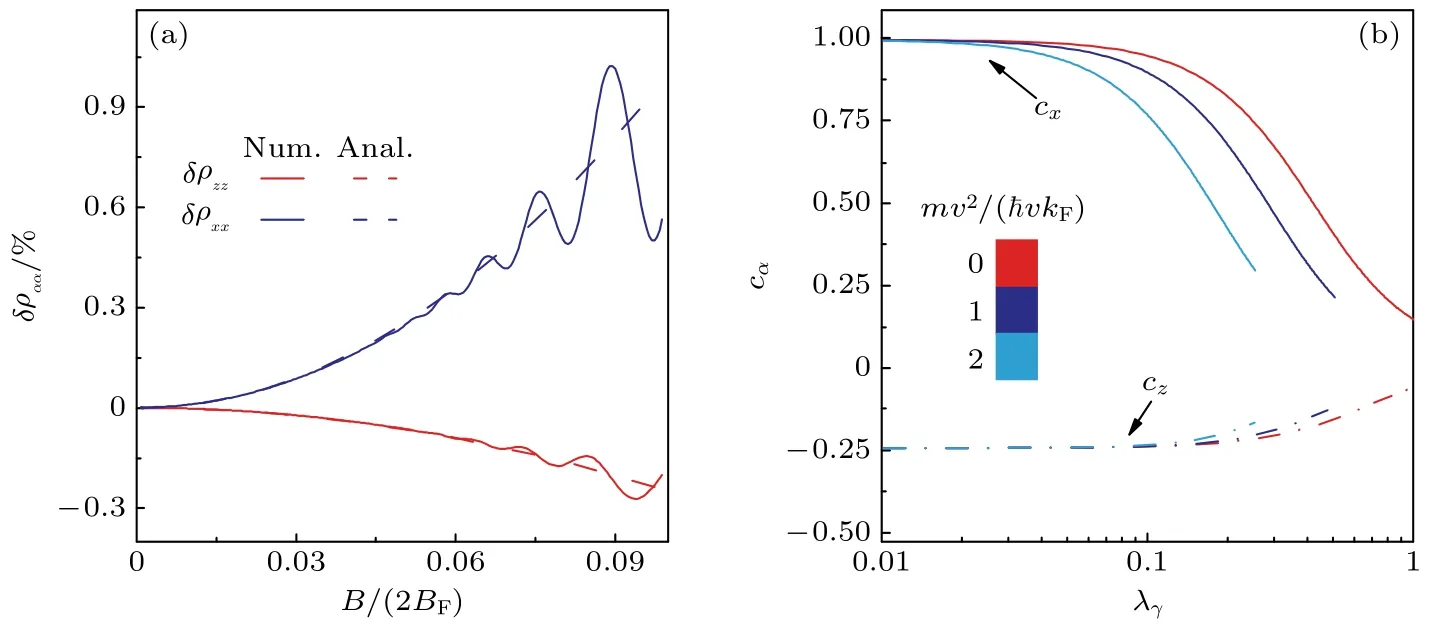
图1 有质量狄拉克费米子的内禀磁阻 (a)有质量狄拉克费米子的横向磁阻和纵向磁阻,其中纵向磁阻为负,横向磁阻为正;(b)无量纲系数随能带展宽的变化关系,cα 在弱散射下趋于一个常数.转载自文献[48]Fig.1.Intrinsic Magnetoresistivity in massive Dirac fermion: (a) Transversal and longitudinal magnetoresistivity,where the longitudinal one is negative and transversal one is positive;(b) dimensionless parameter cα as functions of band broadening,here cα tends to a constant in weak scattering.Reproduced with permission from Ref.[48].
在文献[49]中我们通过求解朗道能级下的量子扩散方程,进一步讨论了有质量狄拉克费米子的负磁阻效应,试图将其与手性反常联系起来.狄拉克哈密顿量中的16 个物理量及无序可以利用5 个反对易的伽马矩阵γµ(µ=0,1,2,3,5)和其派生矩阵来表示,并且根据对称性可以作进一步的分类(如表1 所列).在有质量的狄拉克材料中,有限的狄拉克质量会耦合手性相反的外尔费米子,因此手性不再是一个好量子数.此时轴向电荷(axial charge)连续性方程为
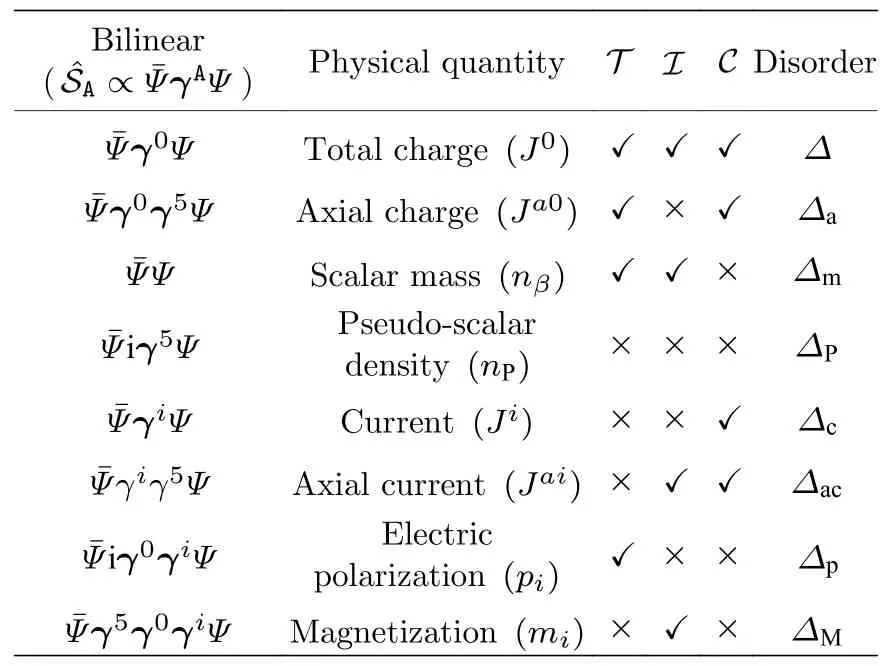
表1 狄拉克哈密顿量中利用狄拉克伽马矩阵表示的16 个物理量及无序根据时间反演(T)、宇称(I)以及手性对称性(C)的分类.转载自文献[49]Table 1. Various types of physical quantities and disorder represented by fermionic bilinears (i=1,2,3),their symmetries under time-reversal (T ),parity (I),and continuous chiral rotation (C).Reproduced with permission from Ref.[49].
表2 4 个库珀子通道 i=s,t0,± 的库珀子能隙(以为单位)和权重因子,其中 η=mυ2/µ 是狄拉克费米子的自旋极化.转载自文献[72]Table 2. Components of four Cooperon channels i=s,t0,± in the basis of spin-triplet and singlet |s,sz〉,the Cooperon gap in unit of the mean free path and the weighting factors wi ,where η=mυ2/µ is the orbital polarization of Dirac fermion.Reproduced with permission from Ref.[72].

表2 4 个库珀子通道 i=s,t0,± 的库珀子能隙(以为单位)和权重因子,其中 η=mυ2/µ 是狄拉克费米子的自旋极化.转载自文献[72]Table 2. Components of four Cooperon channels i=s,t0,± in the basis of spin-triplet and singlet |s,sz〉,the Cooperon gap in unit of the mean free path and the weighting factors wi ,where η=mυ2/µ is the orbital polarization of Dirac fermion.Reproduced with permission from Ref.[72].
方程右侧赝标量密度np的出现表明即使不考虑电磁场的量子涨落,轴向电荷也已经不再守恒.为了理解在有质量狄拉克费米子体系中手性反常和与之相关的负磁阻会被如何修正,在文献[49]中我们基于费曼图技术发展了一套朗道能级下的量子扩散理论.在均匀磁场下,有质量狄拉克费米子的本征能量和波函数严格可解,因此有限磁场下的格林函数可以解析获得.而电场的效应,通过微扰的方式考虑到线性阶.表1 中任意两个物理量的响应系数可以通过虚时格林函数理论计算得到:
在扩散极限下,Γ的空间变化远小于平均自由程(ℓeq ≫1)并且考虑体系经历一系列的碰撞之后的结果(Ωτ ≪1),此时可以获得16 个物理量耦合的扩散方程组.这组扩散方程可以完整刻画有限磁场下狄拉克材料中的输运性质和自旋以及赝自旋弛豫过程.通过求解扩散方程,得到如下主要结论.
i)在磁场下,轴向电荷和矢量电流存在一个正比于磁场强度的反常耦合.由于高朗道能级(n>0)是自旋简并,第零朗道能级(n=0)则是自旋极化的,该反常耦合完全由第零朗道能级贡献.
ii)首先引入一个与体系中破坏手性对称性的机制有关的轴向弛豫时间τa(axial relaxation time).在无质量的情况下,只有质量型的无序(表1中的Δm)会引起不同手性电子之间的散射,从而破坏手性对称性,引入轴向弛豫时间τa.在有质量的情况下,狄拉克质量直接破坏手性对称性,标量无序(表1 中的Δ)就可以引起有限的轴向弛豫时间τa.体系中手性对称性破坏越严重τa越小.平行的电磁场会诱导出一个正比于电磁场强度和τa的手性密度差δρa∝EBτa.
iii)当电磁场方向平行时,轴电荷密度对电流的顶角修正会产生一个正比与磁场平方和轴弛豫时间的纵向电导修正:
结合(16)式,得到有质量狄拉克费米子的轴向电荷连续性方程:
在能隙中,电磁场导致的赝标量凝聚和电磁场涨落导致的量子反常项严格抵消,因此轴向电荷守恒.在导带中,赝标量凝聚的贡献不能被手性反常项完全抵消,此时轴向电荷连续性方程右侧不为零.扩散理论给出了不同于手性反常理论的机制,合理地解释了在有质量狄拉克费米子体系中广泛观测到的负磁阻现象.
在文献[50]中,我们进一步研究了有质量狄拉克费米子的量子反常效应,指出螺旋对称性(Helical symmetry)破缺与负磁阻之间的关系.相比于手性对称性,螺旋度在有质量的狄拉克费米子中仍然是个好量子数.在后面将进一步讨论螺旋对称性破缺引起的负磁阻机制.
4 有质量狄拉克费米子的量子干涉理论
4.1 磁性拓扑绝缘体中的量子干涉理论
在量子扩散区域,由于 π 的贝里相位,二维无质量的狄拉克费米子经历破坏性(destructive)量子干涉,其导致的磁导在零场附近呈现负磁导,这种现象被称为弱反局域化[51,52,66,69,70].弱反局域化效应被视为拓扑绝缘体表面态存在的重要输运特征,并在大量的拓扑绝缘体的材料中被报道[56−63].在有限温下,量子干涉引起的电导修正应该是随着温度升高而减小.然而,实验中观测到的电导修正却是相反的温度依赖关系[59,61,139−141],这一矛盾在没有掺杂的拓扑绝缘体中可以被电子-电子相互作用所解释[70,142,143].在最近的一个关于磁性掺杂的拓扑绝缘体薄膜实验中[63],其磁导具有非单调温度依赖,同时其磁场依赖呈现明显的弱反局域化信号.此时,简单考虑相互作用并不能解释实验上观测到的反常电导修正.在文献[72]中,我们在理论上证明了表面态能谱中由体磁化引起的小质量会对贝里相位有一个温度依赖的修正,进而对表面态相干长度产生新的退相干机制.最终,量子干涉引起的弱反局域化量子修正可以出现非单调的温度依赖.
由于磁性掺杂破坏了时间反演对称性,拓扑绝缘体的表面态会被打开一个有限大小的能隙[144−146].这里将表面态当作有质量的狄拉克费米子进行分析.利用费曼图技术,计算了磁性拓扑绝缘体中由量子干涉引起的电导修正[72],其具有如下形式:
通常σqi的温度依赖主要由相干长度ℓϕ引起,即ℓϕ~T-p/2,这里对于电子-电子(电子-声子)相互作用引起的退相干机制p=1(p=3) .对于磁性材料而言,磁掺杂引起的狄拉克质量也是温度依赖的,因而表面态的自旋极化或贝里相位也将是温度依赖的.此时,温度依赖电导修正的表征参数为
其中ψ(x) 是双伽马函数,是库珀子的磁长度.利用(25)式并考虑狄拉克质量的温度,可以很好地解释实验观测到的非单调温度依赖的电导修正.如图2(a)所示,对于没有磁性掺杂的样品 (xMn=0%),在扣除电子-电子相互作用的贡献以后,磁导随温度升高而变小.而对于有掺杂的样品 (xMn=8%),如图2(b)所示,自旋极化随温度变化引入新的退相干机制,磁导随温度升高非单调变化.
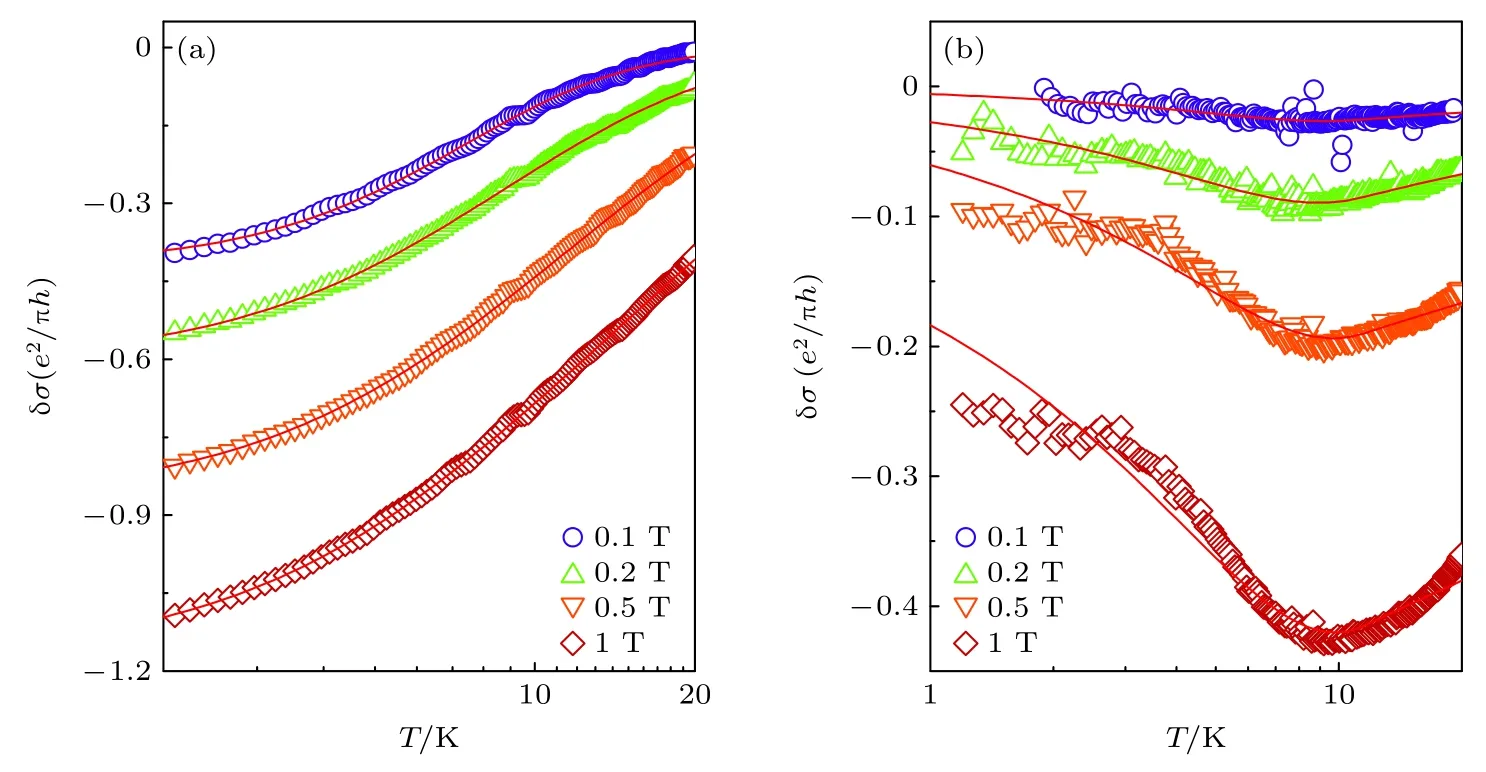
图2 Mn 掺杂的拓扑绝缘体薄膜中磁导在不同磁场强度下的温度依赖行为,其中(a) xMn=0% 和(b) xMn=8% .图中的空心方块是从文献[63]中获得的实验数据,实线是(25)式在不同磁场下的拟合结果.转载自文献[72]Fig.2.Magnetoconductivity as a function of temperature at different magnetic field strength for two Mn-doped topological insulator thin films of (a) xMn=0% and (b) xMn=8% .The open squares are the experimental data extract from Ref.[63].The solid red lines are the fitting results at different magnetic filed B by using the formula in Eq.(25).Reproduced with permission from Ref.[72].
4.2 三维狄拉克费米子中的量子干涉理论
在三维体系中,许多外尔和狄拉克半金属以及拓扑绝缘体当中的磁阻呈现一个非单调的磁场依赖[28,29,32−36,64].之前已有理论都无法解释这样一个磁阻转变行为.这里推导了一个在三维有质量狄拉克费米子中由量子干涉引起的磁阻公式[75].我们的解析公式显示了一个由正到负转变的磁阻行为,揭示了多个弱局域化和弱反局域化通道在不同化学势、有效质量以及有限温度下的强烈竞争.我们使用该理论分析了狄拉克半金属 Cd3As2中的磁阻[64],理论和实验得到了非常好的拟合,这也表明狄拉克材料中由正到负的磁阻转变可以归根于量子干涉效应.为了探讨不同拓扑能带结构下的量子干涉效应,这里使用修正的狄拉克方程(6).
对于三维修正的狄拉克方程,主要有4 个有效的库珀子通道在量子修正中做贡献,分别是无能隙的弱反局域化通道i=0,双重简并的弱局域化通道i=t±,以及弱反局域化和弱反局域化混合通道i=s.在零磁场下,这4 个通道贡献的电导修正为
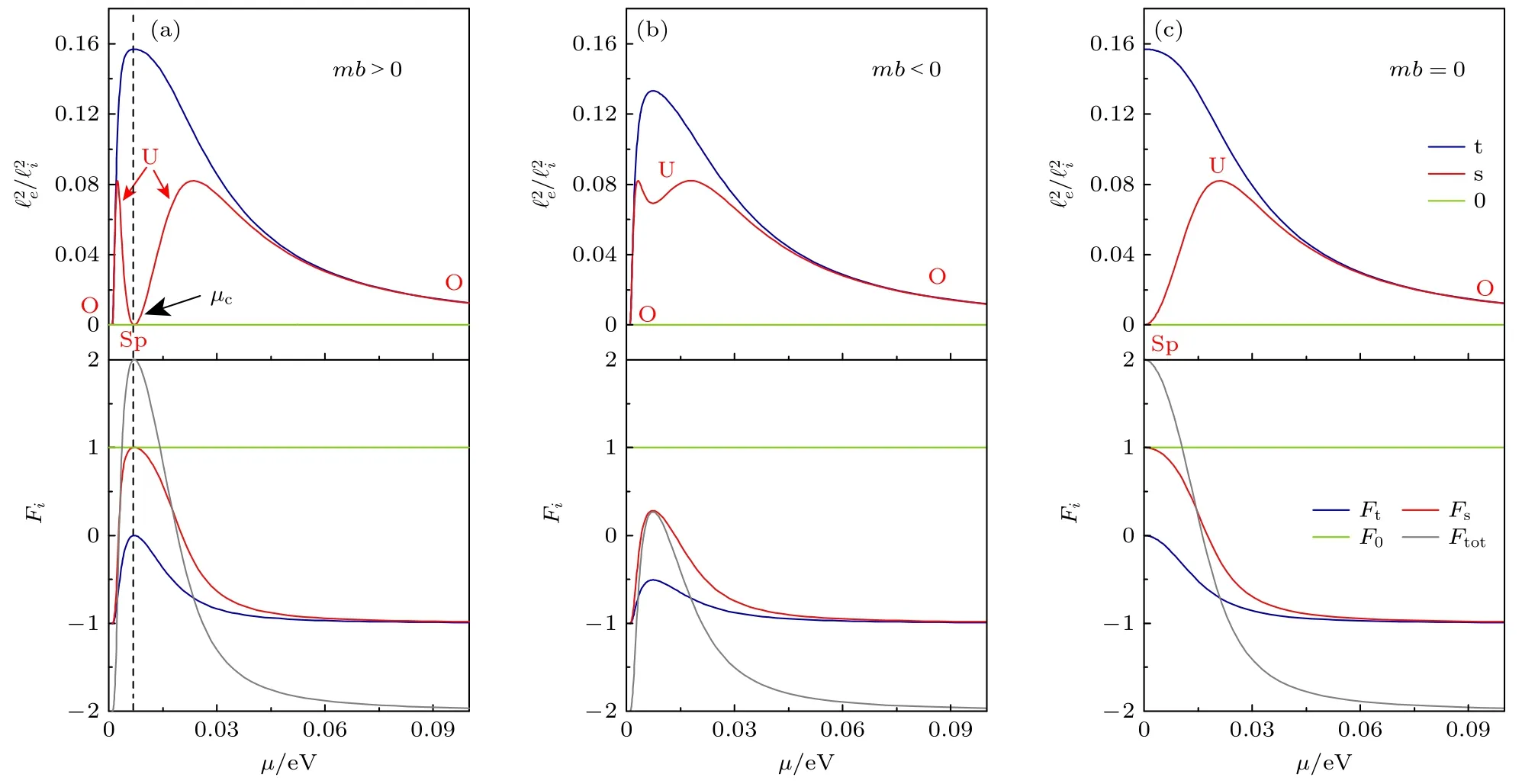
图3 库珀子能隙和权重因子关于能量的函数关系,其中(a) 拓扑绝缘体 (mb >0) ,(b) 平庸绝缘体 (mb <0) ,(c)半金属(mb=0). 是总的权重因子.转载自文献[75]Fig.3.Dimensionless Cooperon gap and weighting factor Fi as a function of the Fermi energy µ for (a) topological insulator(mb>0 ),(b) trivial insulator (mb<0),and (c) Dirac semimetal (mb=0). Ftot is the total weighting factors defined as.Reproduced with permission from Ref.[75].

图4 (a) (27)式对实验中Cd2As3 样品[64]相对纵向磁阻的理论拟合;(b) 拟合得到的相干长度关于温度的函数,可以被ℓϕ ∝T-0.75很好地拟合;(c)不同磁场强度下的相对磁阻关于温度的函数.转载自文献[75]Fig.4.Theoretical fitting to the relative longitudinal magnetoresistance in a Cd2As3 sample[64];(b) fitted phase coherence length ℓϕ as a function of temperatures (open squares),which can be well-fitted by ℓϕ ∝T-0.75 ;(c) measured relative magnetoresistance as a function of temperatures at B=1,2,3 T .Reproduced with permission from Ref.[75].
在有限磁场下,量子干涉引起的电导修正为
除了三维狄拉克费米子,文献[74]和[76]分别对双外尔半金属和节点半金属当中的量子干涉效应进行了研究.双外尔半金属中当单极子荷等于2 时,电子运动一圈获得 2π 的相位,此时时间反演散射态之间产生相干干涉导致弱局域化效应[74].在节点半金属中,量子干涉效应更为复杂.对于短程散射势,电子的背散射由没有环绕节线的干涉路径主导,由于电子经过这些路径后并未积累贝里相位,此时体系呈现三维弱局域化效应(δσ~).而对于长程散射势,电子等效于在二维平面扩散,电子在费米面上环绕节线运动并获得 π 的贝里相位,从而导致具有二维标度的弱反局域化效应(δσ~lnB)[76].
5 ZrTe5 和HfTe5 中的电阻反常
电阻反常是指温度依赖的电阻曲线在有限温T=Tp附近呈现一个明显的尖峰,该效应40 多年前就已经在 ZrTe5和 HfTe5中被观察到[147,148].最初,研究人员认为这种异常现象可能是由于结构相变或者电荷密度波的出现引起的,但很快由于缺乏支持证据而被否定[149−152].近几年越来越多新奇的电和电热效应在这些系统中被探测到[34,85,92,104,153−157],人们也试图重新理解电阻反常出现的物理机制[158−162].例如温度诱导的拓扑相变[160],即能带能隙在升温过程中闭合和重新打开.但是这和实验中的能谱测量不一致[135,163].在文献[121]中,我们提出了一个狄拉克极化子的理论来解释实验上的反常行为.在保证体系中载流子浓度守恒的前提下,狄拉克极化子的化学势随着温度的升高有可能会扫过能隙中间.当化学势呈现这样的行为,体系中就会出现电阻反常.此外,电子空穴在有限温度下的混合会引起反常的电和热电效应.这里首先从各向异性的狄拉克模型出发:
在实际的测量中,电阻反常还伴随着霍尔系数和塞贝克系数的符号转变.对于n-型载流子(µ(T=0)>0),如图5(c)所示,随着温度的升高,霍尔系数RH=∂ρxy/∂B|B=0首先在低温几乎是一个常数(1/en),然后在高温下逐渐减小至最小值,在转变温度Tp附近再由负到正变化.RH的符号改变表明体系的输运性质在温度升高过程中由电子主导变为空穴主导[85,159].塞贝克系数随温度的变化行为和霍尔系数类似.如图5(d)所示,塞贝克系数在低温下随着温度线性变化(Sxx=),并在转变温度附近发生变号.
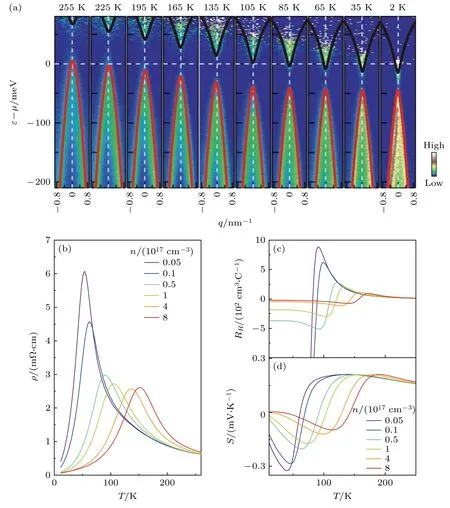
图5 ZrTe5 和HfTe5 电阻反常效应 (a)关于ZrTe5 温度依赖的能谱在实验 (根据文献中ARPES 测量得到) 和理论 (实线) 上的比较,随着温度升高,化学势由导带变化至价带;(b)—(d) 分别为不同载流子浓度下计算得到的电阻反常行为、霍尔系数和塞贝克系数.转载自文献[121]Fig.5.Resistivity anomaly in ZrTe5 and HfTe5: (a) Comparison of experimental (according to the ARPES measurements in literature) and theoretical (solid lines) temperature-dependent energy spectrum.The chemical potential varies from valence band to conduction band with the increasing of temperature.(b)–(d) The resistivity anomaly,Hall coefficients,and Seebeck coefficient for several different carrier concentrations.Reproduced with permission from Ref.[121].
在有限磁场下,横向磁阻ρxx(B) 和霍尔电阻ρxy(B)在接近转变温度Tp和远离Tp时呈现显著不同的行为.如图6(a)和图6(b)所示,在Tp附近,在零磁场附近的横向磁阻ρxx(B) 呈明显的凹陷(dip)行为,霍尔电阻ρxy(B) 关于磁场非线性变化.而对于远离Tp的温度,ρxx(B) 呈现磁场平方依赖,ρxy(B)则恢复为磁场线性行为.同时,在温度接近Tp时,ρxx(B) 在强磁场下也不饱和,这和通常的双载流子模型给出的磁阻截然不同.除了磁阻以外,塞贝克系数Sxx和能斯特系数Sxy在磁场和温度下也呈现出类似的反常行为.如图6(c)所示,塞贝克系数Sxx在磁场下逐渐趋于饱和,其符号随着温度升高而发生变号.而能斯特系数Sxy在磁场和温度下则表现出更为复杂的行为.如图6(d)所示,随着温度升高,Sxy会发生两次变号,并始终表现出很强的非线性行为.Sxy的数值在T~Tp时类似于ρxx在磁场下不饱和.
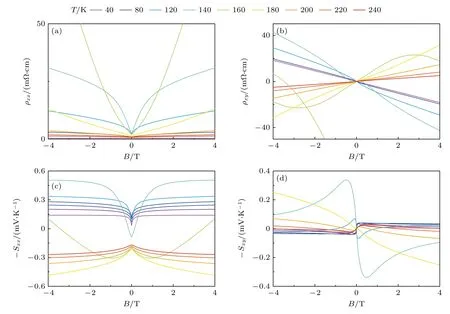
图6 不同温度下的(a)横向电阻,(b)霍尔电阻,(c)塞贝克系数和(d)能斯特系数的磁场依赖.转载自文献[121]Fig.6.Magnetic field dependence of (a) the transverse magnetoresistance ρxx,(b) the Hall resistivity ρxy,(c) the Seebeck coefficient and (d) the Nernst coefficient for different temperatures.Reproduced with permission from Ref.[121].
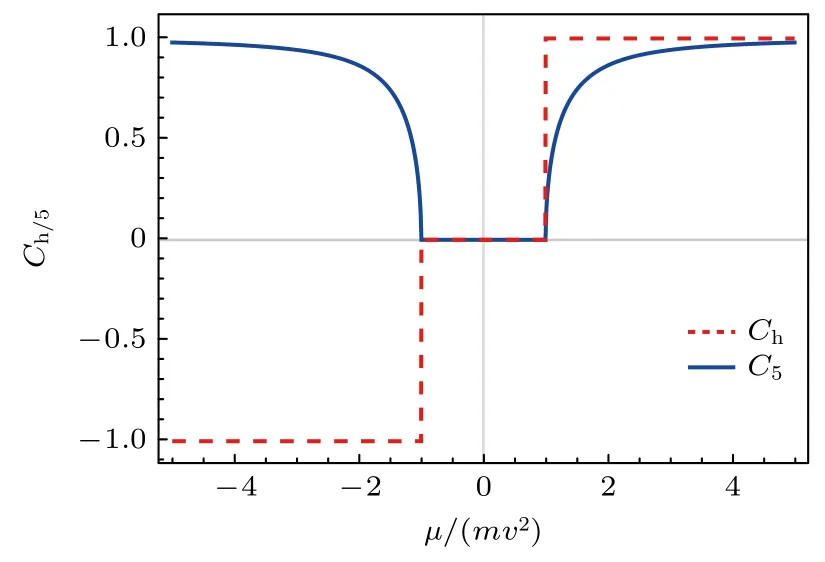
图7 连续性方程(32)和(34)中系数 Ch 和 C5 的比较.转载自文献[50]Fig.7.Comparison of the coefficients Ch/5 in the equations for the divergence of the helical current and axial vector currents in Eqs.(32) and (34).Reproduced with permission from Ref.[50].
文献[159]中利用双载流子模型对电阻反常的性质进行了系统研究,其拟合的结果表明体系的输运性质在温度升高过程由电子主导逐渐转变为空穴主导,体系总的载流子由电子型转变为空穴型.这与上述的讨论明显不一样,这里总的载流子浓度一直保持不变,在温度作用下电子和空穴混合在一起才形成了实验中的反常输运现象.
6 狄拉克费米子中的量子反常效应和螺旋磁效应
无质量狄拉克费米子的手性反常是量子场论中非常重要的一个话题,被认为是由电磁场的量子涨落引起的自发对称性破缺的结果[164−168].具体而言,无质量狄拉克费米子具有手性对称性,根据诺特定理(Noether’s theorem),手性流应该守恒[167].但是由于电磁场的量子涨落效应的存在,手性对称性被破坏,无质量狄拉克费米子的手性流实际上并不守恒.此外,狄拉克费米子还具有螺旋对称性,该对称性在电磁场下被直接破坏.而对于无质量狄拉克费米子,螺旋度和手性等价联系在一起[127,169],那么手性反常是否和螺旋度的直接对称破缺相关呢? 在文献[50]中,我们根据Jackiw-Johnson 的方法[170]推导了关于螺旋电流和轴向电流的连续性方程.在无质量的情况下,这两个连续性方程变得等价.这种等价性证明了螺旋对称性破缺和手性反常的密切联系.在物理测量方面,螺旋对称性的破缺导致了所谓的螺旋磁效应(Helical magnetic effect,即固体材料中存在一个沿着磁场方向流动的电流),以及一个质量依赖的正的纵向磁导.该理论不仅反映了有质量狄拉克材料当中的反常磁输运性质,还显示了螺旋对称性破缺和量子场论中的手性反常的密切关系.根据含时狄拉克方程,可以得到螺旋电流的连续性方程:
其中ψ和为狄拉克旋量,ρh和jh分别是螺旋电荷密度和螺旋电流密度,h是螺旋度算子,V=eEzz是静电势,Ez是电场强度,z是z方向的位置坐标.连续性方程右边第一项是量子涨落给出的反常项,第二项则为螺旋对称性在电场下的直接破缺所导致的.该项的值由第零朗道能级的导带底和价带顶的两个态的占居所决定,每一个态会贡献一个.然后最终的连续性方程为
在这里,当化学势在导带或价带时Ch=sign(µ),当化学势在半填充时Ch=0 .因此直接对称性破缺和量子涨落的贡献在能隙中间恰好被抵消掉.对于无质量的狄拉克费米子,根据手性和螺旋度的关系,可以得到手性电流的连续性方程:
其中ρ5和j5分别为手性电荷密度和手性电流密度.这里从螺旋对称性破缺的角度推导了手性反常的连续性方程.此外,通过计算赝矢量密度的平均值,可以得到有质量狄拉克费米子的手性流的连续性方程:
类似于手性磁效应(chiral magnetic effect),当体系两种螺旋度的电子态存在不平衡时会出现一个正比于磁场的净电流:
7 量子反常半金属
自量子霍尔效应出现以后,拓扑物态和拓扑材料已逐渐成为凝聚态物理当中最前沿的课题之一.在文献[122−125]中,我们提出了量子反常半金属的概念,并讨论了其中新奇的物理现象.下面以二维和三维为例,说明量子反常半金属的奇异性质.
7.1 半整数量子霍尔效应
半整数量子霍尔效应在二维体系中和宇称反常紧密联系在一起[18,91,179−185].在场论中宇称反常是无质量狄拉克费米子的宇称对称性和U(1) 规范不变性之间的冲突产生的[179,180].在文献[123]中,我们讨论了宇称反常半金属(parity anomalous semimetal,PAS)的半整数霍尔效应及其独特的体-边界对应.在材料现实上,有多个体系可以用于实现宇称反常半金属,例如霍尔丹模型(Haldane Model)和三维半磁性拓扑绝缘体.
如图8(a)所示,霍尔丹模型在动量空间有两个狄拉克锥,当其中一个狄拉克锥的能带闭合时,该模型有半量子化的陈数和霍尔电导[18].通过计算,可以得到此时横向电流的空间分布为[123]
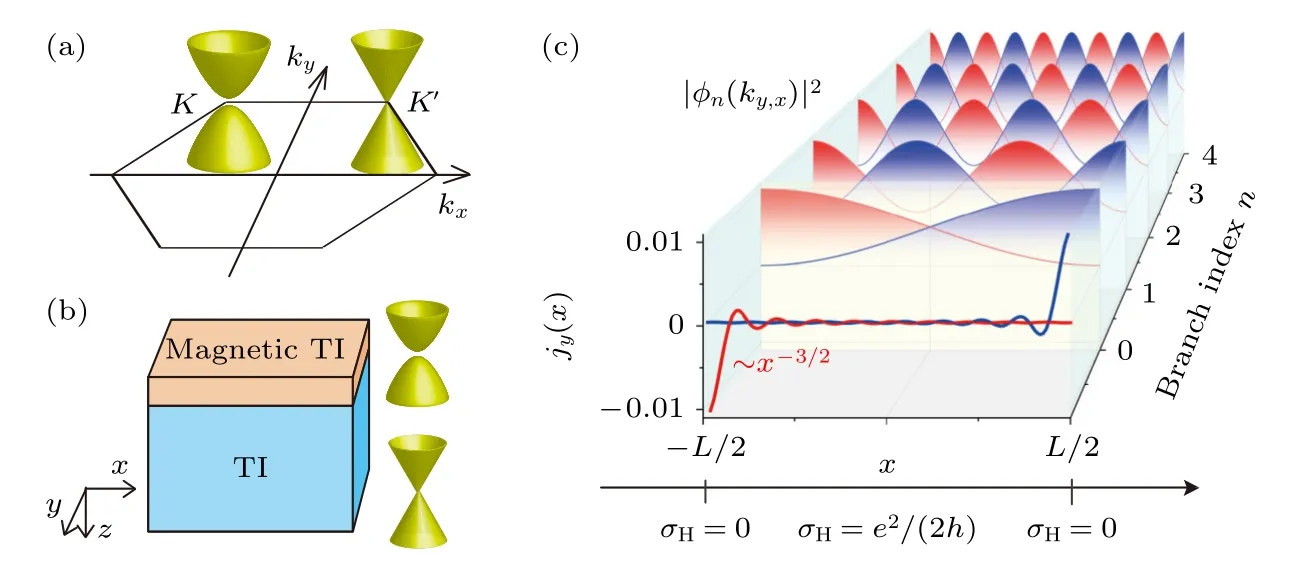
图8 宇称反常半金属示意图 (a) Haldane 模型: 无质量和有质量的狄拉克锥在动量空间分开;(b)三维半磁性拓扑绝缘体: 无质量和有质量的狄拉克锥在实空间分开;(c)宇称反常半金属中低能电子态的分布以及幂律衰减的边界流.转载自文献[123]Fig.8.Illustration of parity anomaly semimetals: (a) Haldane model where massive and massless Dirac cone separated in momentum space;(b) semi-magnetic 3D topological insulator in which a massive and a massless Dirac cone separated in position space;(c) distribution of a set of low energy states and the power law decay edge current in the parity anomalous semimetal for open boundary condition.Reproduced with permission from Ref.[123].
三维半磁性拓扑绝缘体是通过在三维拓扑绝缘体上表面覆盖一层绝缘的铁磁层来形成的[91,186].靠近铁磁层的拓扑表面态因为近邻效应被打开能隙[82,89,91,144−146],而另一个表面的表面态则依然处于无能隙状态.因此在三维半磁性拓扑绝缘体中无质量和有质量的狄拉克费米子在空间上被分开(如图8(b)所示),但是整体依然是半金属态.由于三维半磁性拓扑绝缘体准二维的属性,可以计算空间层分辨的霍尔电导Cz(ℓ),[187−189].Cz(ℓ)主要分布在上表面附近,总的霍尔电导σH=是半量子化的[186,190].类似于霍尔丹模型,也可以计算半量子化霍尔电导对应的边界流.在无能隙的区域,边界流具有幂律衰减的行为~|x±L/2|-3/2,而在有能隙的区域,边界流具有指数衰减的行为.由此可见,半量子化霍尔电导对应了环绕于上表面四周的电流,而此时并不存在棱态 (Hinge States).最近我们针对三维半磁性拓扑绝缘体构建了表面态的格点模型[124],进一步强调了半量子化霍尔电导与无质量狄拉克费米子以及宇称对称性之间的关系.当化学势处在宇称对称性不变的区域,三维半磁性拓扑绝缘体具有半整数量子化的霍尔电导,同时该性质对无序具有很强的鲁棒性.
7.2 1/4 的磁电效应
三维材料中的磁电效应可以由轴子电动力学有效地描述[196].在通常时间反演对称性保护的拓扑绝缘体当中,轴子电动力学中的轴子角θ可以分为两类[8,197],对于拓扑平庸的情况θ=0,对于拓扑非平庸的情况θ=±π .而量子化的轴子角导致了量子化的拓扑磁电效应[184,187,189,198−201].而对于三维量子反常半金属,其具有半量子化的缠绕数,不属于上面两类,那么此时的轴子角θ和磁电效应是什么样的呢,我们在文献[125]中进行了详细的研究.对于三维量子反常半金属,在狄拉克点附近的手性电流满足如下连续性方程:
在b→0 或者kF→0 的时候,三维量子反常半金属的色散几乎是动量的线性函数.在这种情况下体系恢复了手性对称性,然而手性电流却并不守恒,这就表明了三维量子反常半金属在狄拉克点附近具有手性反常,因此也将三维量子反常半金属称为三维手性反常半金属.为了研究三维手性反常半金属中的磁电效应,进一步引进了对称性破缺的项m2τ3σ2,这一项破坏了时间反演对称性和空间反演对称性,但是具有时间反演和空间反演结合的对称性,其通常可以由自旋密度波序(spin density wave order)产生[202−204].在m2趋于 0 的时候,三维手性反常半金属中的轴子角和缠绕数具有如下关系:
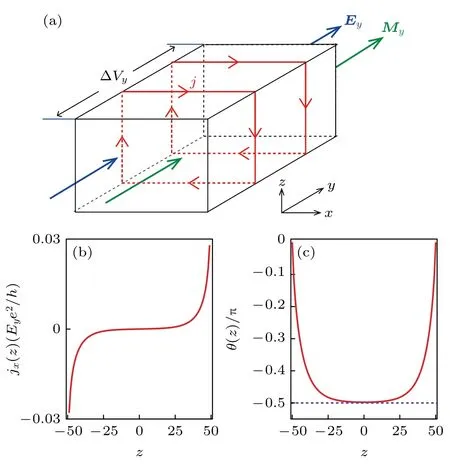
图9 (a)关于磁化强度和体拓扑磁电效应关系的示意图,外加电场产生了表面电流和磁化强度;(b)沿着x 方向的局域电流密度关于位置z 的函数;(c)轴子角 θ 关于位置z 的函数关系.这里电场沿着y 方向.转载自文献[125]Fig.9.(a) Schematic diagram of the relation between magnetization and bulk topological magnetoelectric effect.A surface current is produced by an electric field due to the magnetization.(b) Local current density along the x–direction as a function of slab position z.(c) Spatial dependent θ along the z direction.The electric field is applied along the y-direction.Reproduced with permission from Ref.[125].
其中K0(x) 是第二类零阶修正贝塞尔函数.位置z由变化.可以看出电流jx(z)关于z=0反称,即jx(-z)=-jx(z),然后流过样品总的电流为 0 .如图9(b)所示,电流jx(z) 主要分布在样品上下表面附近的几层.利用K0(x)在x→0 的渐进行为K0(x)~-lnx,可以发现电流在薄膜表面附近具有对数衰减的行为:
这里的对数衰减行为和拓扑绝缘体中的指数衰减行为明显不同,是三维手性反常半金属的一个独特性质.此外,当z偏离薄膜表面时,
其中的衰减长度反比于能隙m2.值得强调的是,由于该体系不存在局域的边界态,这里的表面电流完全由扩展的体态贡献.这种体态贡献的边界流现象在二维宇称反常半金属中同样存在[122,123].
8 评论和展望
狄拉克量子材料是一类特殊的凝聚态体系,其低能准粒子激发具有狄拉克粒子的行为而不能用薛定谔方程描述,比如d 波超导、石墨烯、拓扑绝缘体等都可以认为是狄拉克材料.由于较强电子自旋耦合和非平庸的拓扑性质,人们在其中观测到各种新奇的磁输运现象,其中大量物理现象至今仍未有定论.
本文的第一部分(第3,4,5,6 节)主要是关于狄拉克材料实验中几种新奇磁阻现象的理论解释.在许多有质量或无质量的狄拉克材料的磁阻实验中,小磁场通常表现出正磁阻的行为,随着磁场变大,过渡到负磁阻,呈现出非单调的磁阻行为.小磁场下的磁阻行为通常可以归咎于量子干涉效应.之前的量子相干的磁阻理论大多针对单带无兼并系统,而在很多狄拉克半金属以及拓扑绝缘体体系中,由于同时存在时间反演和空间反演对称性而能带处处兼并,具有内禀的SU(2)对称性,且由于强自旋轨-道耦合而无法解耦,这使得之前的理论方案在这里并不适用.而较大磁场下很强的负磁阻行为通常用手性反常来解释.在很多拓扑外尔和狄拉克半金属材料中观测到的负磁阻行通常被认为是手性反常(chiral anomaly)的直接证据.但是负磁阻现象在一些典型的窄能隙的拓扑绝缘体材料中也被观察到,由于此时狄拉克质量非零,手性不再是个好量子数,左右手粒子耦合,显然手性反常并不能用来解释这些体系中的负磁阻现象.因此急需发展出新的理论框架以更好地处理并解释在这类狄拉克材料里观测到的各种反常磁输运行为.首先基于费曼图技术,我们发展了一套针对狄拉克材料的量子干涉效应的理论方案.该理论不仅成功地解释了一系列实验现象,如狄拉克半金属Cd3As2当中的磁阻、拓扑绝缘体Bi2Se3薄膜中的磁阻反常温度依赖,并且由于完整地考虑了所有的量子干涉通道的贡献,还可以定量研究时间反演对称性微弱破坏的情况下不同通道之间的竞争.多通道竞争所引起的磁阻随着化学势的振荡行为后来在一篇实验工作中得到了验证[205].接着,为了理解较大磁场下的负磁阻效应,我们发展了狄拉克材料的扩散磁输运理论.它可以系统地描述各种无序散射、量子涨落效应、以及自旋和赝自旋弛豫过程.相比于半经典的玻尔兹曼理论,这套基于费曼图的理论对于无序的处理更加微观,并且可以很好地处理能带简并导致的非阿贝尔贝利曲率的情况.通过求解扩散方程,我们得到一个正比于磁场平方的负磁阻.当体系中破坏手性(如狄拉克质量、质量无序等)越严重,该负磁阻越弱.后来我们又注意到,在有限磁场下,无论体系有无质量,螺旋度(helicity)始终是个好量子数,而手性(chirality)只在无质量情况下是好量子数,因此螺旋度在狄拉克材料中比手性更加普适.当两种螺旋度的电子态不平衡时,有限磁场会导致一个平行于磁场方向的电流,即螺旋磁效应.进一步引入两种螺旋度的电子态之间的散射会导致正磁导(负磁阻).该系列工作加深了对于有质量狄拉克材料中负磁阻机制的理解.最后我们指出电声子耦合在窄带隙狄拉克材料有限温度输运中的重要作用,解释了ZrTe5和HfTe5中包括电阻反常在内的一些列电输运和热电输运现象,为理解窄其中的反常输运行为提供了新的思路.
狄拉克量子材料中仍然有很多输运现象未被理解.例如Z2拓扑绝缘体中的线性磁阻机制.根据Onsager 关系,在时间反演不变的体系中,纵向电导率关于磁场的级数展开只存在偶数阶.因此,对于非磁性材料,磁阻通常呈现平方的行为,而对于磁性材料,线性磁阻才允许存在.最近,在一些非磁性拓扑绝缘体材料中观测到这一现象[111−113].实验中发现,在低温情况下,当磁场和电流方向垂直时,横向磁阻随着磁场线性增加,在零磁场处表现出非解析行为,且通常在强场下不饱和.Abrikosov[206]提出在半金属中当载流子只填充在最低朗道能级时(即量子极限),考虑杂质散射,磁阻会表现出线性行为.但是很多情况并不满足量子极限条件,并且由于狄拉克质量的存在第零朗道能级也并不呈现线性.Parish 和Littlewood[207,208]提出当材料的不均匀性非常强时,通过一个经典的电阻网络计算可以得一个不饱和的线性磁阻,但是通常的拓扑绝缘体样品晶体质量很高,因此这个机制不能用来理解拓扑绝缘体中的实验现象.也有一些理论和实验将这个线性磁场解释为拓扑绝缘体表面的贡献[111,114,115].在最近关于拓扑绝缘体材料Bi2Se3的实验中[114],人们发现当磁场方向从面外改变至面内时,线性磁阻呈现出对磁场方向的显著依赖,这是典型的二维特征.并且Shubnikov-de Haas (SdH)振荡给出的载流子浓度也和二维表面态相一致.但是后来有些实验结果表明在一些载流子浓度很高存在体态参与输运的样品中也能观察到二维的SdH 振荡行为[209].王春明和雷啸霖[210]指出在拓扑绝缘体表面态考虑塞曼效应会导致线性磁阻,但是通常实验表明表面态的g因子很小.因此,尽管线性磁阻在拓扑绝缘体材料中被广泛报道,但是迄今为止依然没有统一的理论来解释.另外一个存在争议的是ZrTe5中的三维量子霍尔效应和反常量子霍尔效应.自从量子霍尔效应在二维发现以来,人们一直试图将其推广到三维.相比于二维,三维霍尔电导率会有一个额外的长度分之一的量纲.在1983 年,Avron 等[211]提出当三维体系中层间耦合很弱,磁场对应的朗道能级能量大于层间耦合时,体系表现出准二维的性质从而霍尔效应表现出晶格常数分之一的量子化.但是当层间耦合变强时,体系会变成金属,这个图像并不成立.在三维金属中,Halperin[212]提出相互作用会导致自旋密度波或是电荷密度波的形成从而出现能隙,最终实现正比于费米波矢的量子化霍尔电导同时纵向电导为0.最近,在ZrTe5和HfTe5的磁输运测量实验中[85,157],观测到在量子极限下正比于费米波矢的量子化霍尔电导,而且SdH 振荡的结果表明费米面是个椭球而不是准二维的开放结构,并且测到非欧姆的I-V曲线.其后卢海舟课题组[88,213]基于平均场和重整化群的理论工作认为在这个体系中量子化霍尔电导是由于电荷密度波的形成,并且可以自洽解释实验现象.但是另外一些工作中,也存在一些不同的结果.例如有些实验工作表示,量子化的霍尔电阻伴随一个非零的纵向剩余电阻,另外一些关于热电输运的实验中也表示没有观测到电荷密度波形成的信号[86,120].霍尔系数是霍尔电阻对磁场的导数.根据经典的Drude-Boltzmann 理论,霍尔系数不依赖散射机制,只依赖于体系载流子浓度,因此实验上通常被用来测量载流子浓度.当体系不存在电子或空穴掺杂,体系载流子浓度保持不变的情况下,霍尔电阻呈现出磁场的线性依赖.但是最近在一些ZrTe5的磁输运实验测量中[92−97],霍尔电阻表现出非线性的行为,甚至在强磁场下出现斜率变号.在零磁场下ZrTe5是非磁性材料,反常霍尔电导为0,因此磁场下塞曼劈裂非常重要.并且当费米能量不在能隙中时,反常霍尔电导除了由内禀的贝利曲率贡献外,侧向跳跃(side-jump)和斜散射(skew scattering)导致的杂质散射也有贡献[214].而在磁场下ZrTe5表现出的非线性霍尔电阻的理论机制至今仍存在争议.
第二部分(第7 节)介绍一类与量子反常密切相关的新型狄拉克半金属相及其输运性质.在二维,我们基于量子场论中宇称反常(parity anomaly)的概念提出宇称反常半金属,并进一步建立了它的体边对应关系.所谓的宇称反常是指与规范场耦合的2+1 维无质量狄拉克费米子无法在同时保证宇称对称性和规范不变的方式量子化.在有效场理论中,当作用量中的费米子部分被积掉之后,可以得到一个关于规范场的Chern-Simons 项,对应1/2分数量子化的霍尔电导.虽然宇称反常的概念已经被提出将近40 年,但是直到最近由于狄拉克材料的深入研究,半整数化的量子霍尔效应才在实验中被观测到.整数化的量子霍尔效应及其拓扑体边对应关系已经被研究清楚并且被广泛接受.但是对于半整数量子化的量子霍尔效应的体边对应关系还并不清楚.我们通过严格解和数值方案建立了半整数量子霍尔效应的体边对应.与整数量子霍尔效应体系不同,具有半整数量子反常霍尔效应的宇称反常半金属中没有良好定义的边缘态,但是延展的体态会集体贡献出一个局域在磁性和非磁性界面处的边界流,且这个边界流表现出幂律衰减的行为.接下来在一维和三维中,我们基于手性反常(chiral anomaly)的概念提出手性反常半金属.这是一类只有单个狄拉克点并且具有子格对称性(属于AIII 对称类)的特殊拓扑半金属.其拓扑性质可以用一个半整数的缠绕数来刻画,对应 1/4 分数化的拓扑磁电效应.这系列工作将整数拓扑量子态推广到分数并且确立了其反常体边对应关系,即具有半整数的拓扑数的量子反常半金属没有良好定义的边缘态但具有分数化的拓扑边缘效应.
除了半磁拓扑绝缘体,宇称反常半金属中幂律衰减的边界流同样适用于量子反常霍尔效应和轴子绝缘体(axion insulator,AI)[191−195].以往对这两个体系的理解是基于上下表面态的霍尔电导,分别 为. 然而在这个图像下侧面表面态的贡献完全被忽略了.我们的理论计算显示,幂律衰减的边界流存在于有质量和无质量狄拉克费米子的界面处,量子反常霍尔效应和轴子绝缘体中的表面霍尔效应均可基于宇称反常半金属的理论进行解释.轴子绝缘体由三维拓扑绝缘体上下表面分别覆盖相反磁矩的铁磁层形成,无能隙的侧面表面态处于两个有质量表面态中间,且上下表面态的狄拉克质量符号相同.此时轴子绝缘体的侧面电流的分布和宇称反常半金属一样.不同的是,由半磁拓扑绝缘体形成的宇称反常半金属中无质量狄拉克费米子所处的区域长度为LPAS=w+2d,而轴子绝缘体中无质量狄拉克费米子所处的区域长度为LAI=d,其中w和d分别为样品的宽度和厚度.通过对(37)式中电流分布进行积分,可以得到某个表面附近贡献的霍尔电导为.对于半磁拓扑绝缘体,样品宽度w比较大(约 100 μm),kFw→+∞,F(kFLPAS)→1(如图10 所示).因而体系有很好定义的半整数量子化的霍尔效应.对于磁性拓扑绝缘体薄膜形成的轴子绝缘体,往往需要将化学势调节到狄拉克点附近,例如kF~0.1 nm-1,而样品的厚度只有几个纳米,因此kFd的数值往往比较小(1 的量级).如图10插图所示,,相关的表面霍尔电导,一边为,另一边为.只有当样品足够厚使得kF d→+∞,体系才有可能给出半整数量子化的霍尔效应,例如让样品厚度增加至几百纳米甚至微米量级.但此时侧面的表面态为无能隙的狄拉克电子,霍尔电流主要由这些表面态提供.在文献[215]中,我们针对磁性拓扑绝缘体中的宇称反常半金属、轴子绝缘体和量子反常霍尔效应三种状态的霍尔效应的能带拓扑进行进一步的研究.在能带计算中,只能得到宇称反常半金属的半整数量子霍尔效应,而轴子绝缘体和量子反常霍尔效应中并没有发现半整数量子霍尔存在的确切迹象.此外,文献[216,217]对半磁拓扑绝缘体和轴子绝缘体中的半整数霍尔效应也进行了讨论.文献[216]将半磁拓扑绝缘体中半整数量子化的霍尔电导归功于沿着经典金属(classical metal)边缘传播的半量子化的手性流,其大小在低温下不依赖于化学势和温度的大小.文献[217]建立了半量子化手性流与古斯-汉欣位移电流(Goos-Hänchen shift current)的关系[218],并指出古斯-汉欣位移在轴子绝缘体中是半量子化的.接下来还需要更多的实验和理论来区分半整数量子霍尔的不同物理机制和图像.
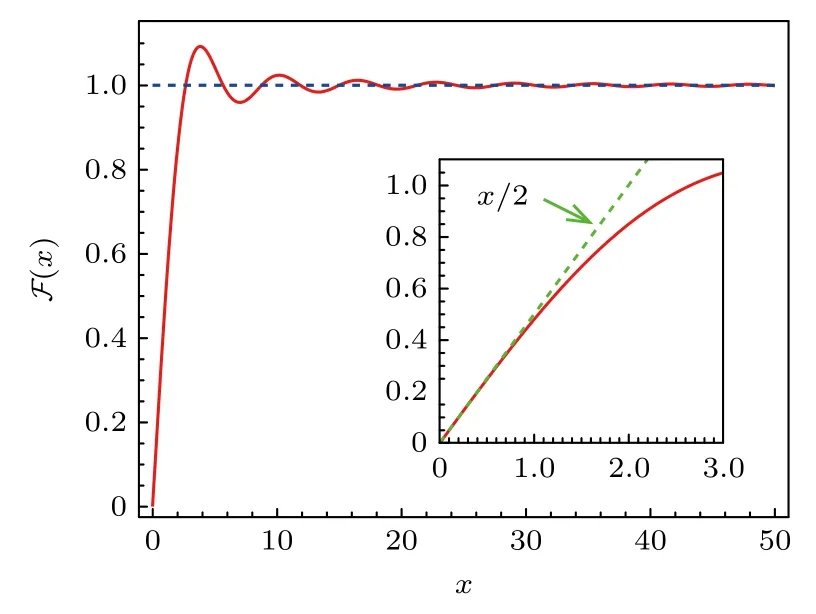
图10 F(x) 关于x 的函数关系,其中蓝色虚线表示F(x)=1 的位置.插图是 x≤3 的函数曲线,绿色虚线是x→0 下的线性拟合F(x)=x/2Fig.10.Function relation between F(x) and x,the dashed blue line indicates the position of F(x)=1 .Insert is the function curve for x≤3,the dashed green line is the linear fitting with F(x)=x/2 for x→0 .
