自旋简并节线半金属中表面态诱导的自旋相关散射*
2023-09-19刘力硕陈伟
刘力硕 陈伟
(南京大学物理学院,固体微结构物理国家重点实验室,人工微结构科学与技术协同创新中心,南京 210093)
拓扑节线半金属指的是电子的导带和价带在倒空间相交于一维的环或者线,其体能带拓扑体现在节线携带π 的贝里相位.根据体边对应原理,在系统边界存在色散较弱的表面态,由节线在表面布里渊区的投影所包围,称为鼓面态.大部分节线半金属中,自旋-轨道耦合效应较弱,因此在单粒子图像下表面态不存在自旋构型.与此同时,鼓面态特有的弱散射也使得其中的电子间相互作用效应变得显著,并诱发铁磁失稳使得自旋简并的表面态发生自旋劈裂.本文考虑自旋简并的节线半金属中铁磁表面态导致的自旋相关散射,发现自旋劈裂的两个鼓面态均会导致共振的自旋翻转反射,该物理过程体现为自旋电导谱中的双峰结构.具体地,分别用散射矩阵和格林函数理论处理了普通金属和节线半金属异质结中表面态导致的散射问题,得到一致的结论.本文的工作指出了自旋简并节线半金属表面态依旧可以导致自旋相关输运,这为其输运探测和在自旋电子中的应用提供了新的思路.
1 引言
近十几年,拓扑材料(包括拓扑绝缘体、拓扑超导体和拓扑半金属)吸引了广泛的研究兴趣[1,2].这一方面是由于对拓扑物态的刻画超越了传统的朗道相变理论,伴随着全新的物理现象;另一方面,拓扑材料的新奇物理特性也呈现出若干重要的应用前景,如拓扑量子计算、低功耗电子器件等[3].朗道相变理论使用不同的局域序参量刻画不同的物相,而不同的序参量对应着不同的对称性破缺.随着整数(分数)量子霍尔效应的发现[4,5],大家意识到存在无法用局域序参量描述的物质相,与之对应的,相变过程中也不伴随对称性的破缺.新的相由封闭流形的全局性质来区分,具体体现在拓扑不变量的取值.只要流形的拓扑性质不变,该拓扑相也不会改变,这预示着材料的拓扑相具有抗微扰的特性.拓扑材料所处的外部环境——真空,可以被视作一个拓扑平庸的绝缘体,而材料和真空具有不同的拓扑不变量,不能连续过渡到彼此,因此,在它们的界面通常会存在奇异的拓扑表面(边缘)态.这是拓扑物态的一个普遍特征,称为“体边对应”原理,即“体”态具有非平庸拓扑,则“边界”上就会出现零能隙的表面态[6].由于边界态的出现与材料的拓扑性质直接关联,这些态具有非常强的鲁棒性,电子在其中的传输也能展现出低耗散的特征,有望被应用于低功耗电子器件.此外,由于表面态电子与体电子之间的关联,材料会演生出更丰富的等离激元,有望用于高热稳定性的等离激元器件、光学器件[7,8].
根据材料导带、价带是否简并,非超导拓扑材料还可细分为拓扑绝缘体[1]和拓扑半金属[9].其中,拓扑半金属还可以根据导带、价带的简并构型分为狄拉克半金属[10]、外尔半金属[11,12]、节线半金属[13]等.狄拉克半金属和外尔半金属的导带、价带在布里渊区的一些孤立点发生简并,且在简并点附近电子能量具有线性色散关系;节线半金属的简并点形成一维的环或者线,或者其他更复杂的一维构型.这些拓扑半金属的能带拓扑,通常可以通过“降维”法来理解,等价为包含参数(动量)的低维拓扑绝缘体.根据体边对应原理,这些拓扑半金属亦会在其表面形成奇异的拓扑表面态,如外尔半金属中的费米弧态.虽然拓扑半金属的表面态在数学上可以利用带参数的拓扑绝缘体模型进行理解,但真实的拓扑半金属材料性质与拓扑绝缘体有本质的区别,这就是在费米能处体态和表面态是共存的.二者的共存或可带来更为丰富的物理效应,但同时也为拓扑表面态的探测带来了困难.
本文主要关注节线半金属表面态的性质及其探测.考虑最典型的节线半金属,其体能带简并发生在一个环上.相应地,在其表面布里渊区存在拓扑表面态,范围为节线环的投影面积,被形象地称为“鼓面态”[14].对鼓面态的探测是验证节线半金属相的直接手段.目前,被广泛用于探测拓扑材料电子性质的实验方法包括角分辨光电子谱(ARPES)[15-17]和量子振荡[18,19].在ARPES 实验中,表面电子、体电子会同时被光子激发,因此表面态的信号与体信号混合;在量子振荡实验中,参与物理过程的主要是体电子,因此很难观察到表面态的信号.通过在材料表面构筑输运器件的方式,表面态可以直接通过输运方式被探测.在具有强自旋-轨道耦合的节线半金属中,鼓面态可以发生自旋极化.若入射电子平行于界面的动量位于节线环投影内,并且其能量低于相应通道的能隙,则电子会被反射回去;有趣的是,由于自旋-轨道耦合导致的表面态自旋极化,电子被反射时会伴随自旋翻转.当界面势垒较大时,电子会发生共振自旋翻转反射,且该共振条件与决定节线半金属表面态的量子化条件一致[20].这说明共振自旋翻转反射反映了节线半金属表面态信息.在这一机制下,外接电极与表面态拥有最强的耦合,可以有效提取出鼓面态的信息,反映为自旋电导或者普通电导谱中的单一共振峰结构.但大多数节线半金属的自旋-轨道耦合很弱,在不考虑电子间相互作用时鼓面态具有自旋简并,不会诱导出自旋翻转反射,这就限制了以上输运方案的应用.
注意到,节线半金属表面态的一大特点是具有较弱的色散,与之相对应的是增强的电子间库仑相互作用效应.本文考虑库仑相互作用导致鼓面态中的斯通纳(Stoner)铁磁失稳,会在系统表面形成铁磁序[21,22].这一表面铁磁序将导致鼓面态发生自旋劈裂(见图1),变为两组自旋沿着相反方向极化的态.由于表面态在电子间相互作用下获得了自旋极化,且相反极化方向的态在能量上可区分,因此它亦可以导致自旋翻转反射.与具有自旋轨道耦合的节线半金属中单一自旋极化表面态不同的是,这里存在两组自旋(反向)极化的表面态.可以预期,自旋相关输运现象将由它们的共同作用决定.本文建立了描述普通金属-节线半金属异质结的有效模型,并通过非对角界面散射势来模拟表面铁磁序的作用.结果表明,自旋极化的两组鼓面态会导致共振自旋翻转反射,这一效应表现为自旋电导谱中的双峰结构,分别对应自旋劈裂的两组鼓面态的贡献.进一步,通过格林函数方法证实了这一自旋相关散射过程确实来自于自旋极化的表面态.当鼓面态存在有限色散时,原本自旋电导谱中的关于零能量对称的双峰结构将变得不对称,但双峰的基本形态依旧保持.本研究为具有自旋简并的节线半金属中鼓面态的探测提供了理论方案.
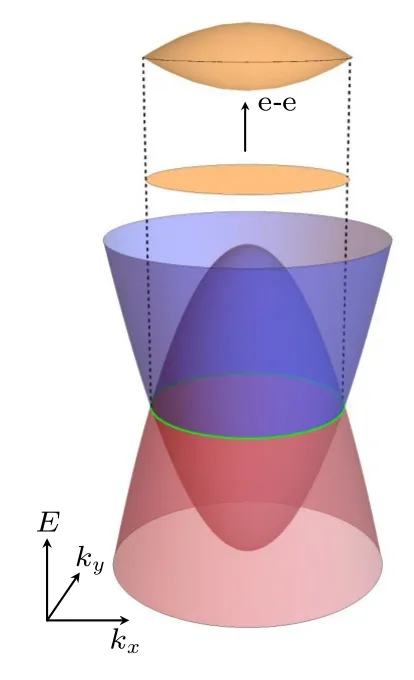
图1 节线半金属鼓面态自旋劈裂示意图.绿色实线表示节线环,饼型圆盘表示劈裂后的鼓面态色散关系Fig.1.Schematic diagram for the spin splitting of the drumheadlike surface states.The green solid line represents the nodal loop,and the pie-shaped disk represents the dispersion relationship of the spin-splitting drumheadlike surface states.
2 理论模型和方法
节线半金属可由如下低能有效模型进行描述,它的哈密顿量为[23]
根据巡游磁性的斯通纳理论,在零温时系统自发形成铁磁序的条件为Uρ(EF)>1,其中U为短程库仑相互作用强度,ρ(EF) 为系统费米面处态密度[26].本文假设体能带处于半填满状态,因此态密度由鼓面态贡献.由于鼓面态色散很弱,费米面处具有很大的态密度,因此容易发生铁磁失稳形成表面铁磁序[21,27].该铁磁序会在表面处产生一个有效的塞曼场,使简并的鼓面态发生自旋劈裂[21,27].值得注意的是,表面铁磁序所致的鼓面态自旋劈裂大小是依赖于面内动量k//的,可以理解为一种自旋依赖的色散.其原因在于对不同的k//,表面态向体内的延展深度是不同的.k//越是靠近节线,则该通道中能隙Δ(k//) 越小,表面态往体里扩展得也就越深,感受到表面塞曼场的有效作用越弱.因此鼓面态的自旋劈裂如图1 所示,越是远离节线自旋劈裂越强,在节线处表面态恢复简并.
接下来,考虑一个普通金属-节线半金属异质结体系,界面处包含鼓面态,设界面在z=0 处.电子在该界面发生的散射应当包含自旋劈裂鼓面态的信息.假设界面足够平滑,使得面内动量k//在散射中守恒,则散射问题也可以降维成一系列k//通道中的一维问题.可以在实空间写出整个系统的哈密顿量,以k//为模型参数,它具有以下形式:
其中,C(z)=Cθ(-z) 是有效质量相关参数 (θ为阶跃函数),µ(z,k//)=(µ0-C|k//|2)θ(-z) 是有效化学势,这两项给出z<0 区域普通金属的哈密顿量,普通金属哈密顿量在赝自旋τ和真自旋σ空间均是对角的;λ(z)=λθ(z),B(z)=Bθ(z),{λ(z),∂z}是反对易子,这3 项给出 (z>0) 区域节线半金属的哈密顿量;Dδ(z)σx代表界面处x方向的塞曼场,唯象地刻画表面铁磁序.这里假设塞曼场方向沿着x方向是不失一般性的,如果同时旋转塞曼场的方向以及入射电子自旋的极化方向,将得到不变的结果.上述参数都随空间坐标变化,为了使哈密顿量满足厄米性,(2)式中所有项都做了对称化处理[28,29].由于本文考虑的是自旋劈裂后的散射过程,所以上述哈密顿量的旋量部分为赝自旋与自旋的直积.这里有必要对上述模型做一些额外的说明: 首先,在该异质结界面处,鼓面态天然存在,隧穿极限时节线半金属表面所处的物理条件与真空界面并无二致;其次,这里的Dδ(z)σx势描述了局域在表面的塞曼场,它可以导致自旋翻转,并叠加上鼓面态的作用产生共振效应,该形式使得表面铁磁序的作用可以被方便地写进边界条件.
求解该异质结中的散射问题需要寻找合适的边界条件,从而使整个散射过程满足流守恒条件.由于哈密顿量中存在狄拉克型界面势和坐标的一阶导数项,波函数的一阶导数将在界面处发生突变.将哈密顿量在界面处积分,得到波函数导数的匹配条件;同时,波函数还需要满足连续性条件,因此可以归纳边界条件如下:
接下来考虑散射问题,假设自旋向上(沿z方向极化),平行动量满足|k//|<k0的电子从普通金属入射到异质结界面,电子动量方向与z轴夹角为θ.此处为了数学上方便处理,在普通金属中依旧保留了赝自旋自由度,但最终的物理结果显然与该赝自旋是无关的.如此,波函数就包含4 个分量,写为,下标 1,2 分别代表赝自旋的两个分量,上标↑,↓代表自旋的方向.考虑以分量和能量E从普通金属中入射的电子,相应的散射态波函数为
自旋翻转反射可以通过自旋电导来反映,它可以通过兰道尔(Landauer)公式表达为反射系数的函数.对给定的导电通道k//,自旋流(I↑-I↓)对应的微分电导表达式为
其中,Rc=|rc1|2+|rc2|2为自旋守恒的反射概率,Rf=|rf1|2+|rf2|2为自旋翻转反射概率,这里的求和相当于对赝自旋部分取迹,因为这部分物理自由度在普通金属中并无真实物理对应.注意到,自旋守恒的反射贡献与入射电子相反的自旋流,而自旋翻转反射电子贡献与入射电子相同的自旋流(速度、自旋同时反号).类似地,电流I=I↑+I↓对应的微分电导为
两种反射均贡献相反的电荷流.
每个一维导电通道都对自旋输运有贡献,因此系统的自旋电导需要对所有k//通道求和,这里考虑主要贡献来自节线环内部:
其中,A为金属-节线半金属界面的面积.将表达式由动量空间的直角坐标系变换到极坐标系,自旋电导的表达式改写为
3 结果与讨论
这里主要关注自旋翻转反射发生的概率Rf(E,θ)随入射能量的变化,不同入射角θ下的结果如图2 所示.可以看到,结果具有两个主要特征:首先,对所有入射角(通道),自旋翻转反射均呈现出双共振峰的结构;其次,对不同入射角,双峰的位置是不同的.双共振峰的结构与鼓面态的自旋劈裂图像是一致的,沿着x方向相反极化的鼓面态,均可以导致沿着z方向自旋极化的入射电子发生自旋翻转反射,但共振能级关于零能量对称(见图1).而对不同的入射角,我们知道鼓面态自旋劈裂的大小是不同的,越是靠近节线的通道,能量劈裂越小,因此共振峰也就越接近,如图2 所示.若在一维有效模型中添加额外的异质结界面势垒,这将破坏体系的手征对称性.此时,自旋翻转反射的双共振峰结构依然存在但不再对称.因此,唯象地引入界面非对角散射势D确实可以对表面铁磁序导致的共振自旋翻转反射进行一个简单而有效的描述,并给出定性正确的结论.这里非对角散射势的作用分为两部分,一部分为表面塞曼场的作用,一部分为界面势垒的作用.当然,这种简化的描述也有它的不足之处.例如,图2 中的共振峰处散射概率并不能达到100%,共振峰随着角度的展宽变化也不一定有真实的物理来源.要严格处理该问题,需要首先自洽求解z方向空间分辨的铁磁序,并用相应的空间分辨塞曼场代入模型中进行计算,我们留作今后进一步讨论.

图2 电子自旋翻转反射与能量的依赖关系.θ 为入射电子与z 方向夹角,Δ0=Δ(k//=0) 是电子垂直入射时的有效能隙.相关参数取 B=C=1 eV·nm2,λ=0.01 eV·nm,|kF|=1.1k0=1.54 nm-1,D=3 eVFig.2.Probability of electron spin-flipped reflection Rf vs.E for different angles of incidence θ (relative to z axis).Δ0 is the effective energy gap when θ is zero.Relevant parameters take: B=C=1 eV·nm2,λ=0.01 eV·nm,|kF|=1.1k0=1.54 nm-1,D=3 eV .
自旋极化鼓面态导致共振自旋翻转反射这一结果,来源于量子力学中共振条件与束缚态形成条件的对应关系[20].这一普遍联系也可以通过隧穿哈密顿量来进行刻画.假设k//通道中的表面态发生自旋劈裂后,能量分别为E+、E-,且E+=-E-.劈裂后鼓面态波函数的空间部分为,该波函数向材料体内衰减.假设鼓面态自旋沿x方向极化,则E±对应的自旋旋量为,相应地,鼓面态波函数分别为.定义自旋劈裂表面态的费米子算符为γ±(k//),在低能下,系统费米子算符可以用表面态算符表示为
普通金属作为电极,其哈密顿量为
其中能量为εk=C|k|2-µ0.金属电极直接与材料表面耦合,因此能最大程度地感受到表面态的效应.普通金属与节线半金属耦合的隧穿哈密顿量可以写为
其中tk为耦合强度.低能下,普通金属仅耦合表面态自由度,代入(10)式,隧穿哈密顿量约化为
为了描述表面态导致的自旋翻转反射,先求解表面态的推迟(R)、超前(A)格林函数:
其中的对角元表示从自旋极化的表面态透射到普通金属又重新透射回原来的表面态,而非对角元对应于从某一自旋极化的表面态透射到普通金属后被散射回自旋极化相反的另一表面态.
考虑耦合系数随着k缓变,并将其视作常数,且自能项实部是关于εk的奇函数,这里只取自能虚部并将其记为,并得到相应地线宽函数为
利用非平衡格林函数理论中计算散射系数的公式Rf(E)=Tr[Γ↑GA(E)Γ↓GR(E)][30,31],并代入格林函数(14)式和线宽函数(16)式可以求得自旋翻转反射概率为[27]
(17)式的前两项表现为在表面态能级处的洛伦兹型共振峰,最后一项显示出两个能级之间的相互作用.在隧穿极限Γ→0 下,第二项可以忽略,共振峰严格在表面态处;随着普通金属与节线半金属耦合变强,两个峰逐渐展宽,并相互接近.数值结果如图3 所示,该结果进一步佐证了自旋劈裂的鼓面态可以导致自旋翻转反射的双共振峰结构,与基于界面散射势的有效理论有一致的结论.
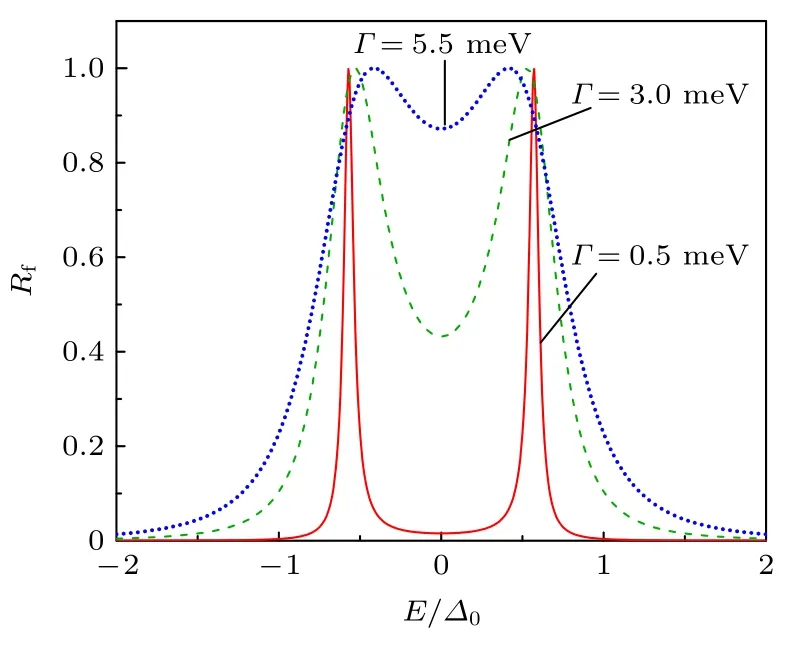
图3 隧穿哈密顿量方法求得的自旋翻转反射系数.相关参数取 E-=-E+=8 meV,Γ=0.5,3.0,5.5 meVFig.3.Probability of spin-flipped reflection solved by Green's function as a function of energy with the following parameters: E-=-E+=8 meV,Γ=0.5,3.0,5.5 meV.
真实的节线半金属往往具有多种表面态,包括鼓膜态(由材料能带拓扑性质导致)、杂化表面态(由表面势导致)、悬浮表面态(由非同态对称性在材料表面破缺导致)[8].鼓膜态与后两者的区别主要在于它相较于其他表面态具有较强的鲁棒性,且色散较小,容易发生铁磁失稳.后两种非拓扑表面态受表面势影响极大,且具有与体能带接近的色散强度,能量范围远大于鼓膜态.可以预期,杂化表面态和悬浮表面态虽然位于材料表面,但其表面态能量范围很大,不会像鼓膜态一样形成双峰结构,仅能贡献一均匀背景.
对自旋电导 (8)式和普通电导 (9)式的两个表达式做数值积分,得到图4 中的结果.可以看到,在能隙Δ0以内,普通电导G被强烈抑制,因为几乎所有入射电子都被反射回普通金属中;与此同时,自旋电导表现为关于零能量对称的两个峰,这主要是由不同k//通道中发生的共振自旋翻转反射所贡献.当然该双共振峰结构并没有单通道反射系数那么尖锐,这是由于不同通道的共振能级有相对偏移所致,整体抹平了共振效应.上述结果基于鼓面态是完全平的这一假设,而在实际材料中,节线半金属的鼓面态本身就存在弱的色散(这里指的色散不是表面塞曼场引入的,而是不考虑电子间相互作用时简并表面态就拥有的).可以预期的是,鼓面态本身的色散将打破表面态关于零能的对称性,因此自旋电导和普通电导亦会表现出正负能量不对称.这一效应可以通过修改散射系数的能量依赖关系看出来.不失一般性,考虑鼓面态具有一弱的抛物型色散 δE=a(k0-|k//|)2,并且保持在节线环边缘处鼓面态为零能.假设鼓面态对于零能的偏移很小,其向体内衰减长度几乎不变,因而表面塞曼场的描述不变.鼓面态色散导致的效应体现在不同的k//通道偏移不同的能量,相应地,其散射系数关于能量的函数也发生偏移.具体地,有Rf(θ,E)→Rf(θ,E-δE)以及Rc(θ,E)→Rc(θ,E-δE) .将代换后的散射系数重新代入(8)式和(9)式,得到数值结果如图4 所示.可以看到,双共振峰的结构依旧存在,但两个峰的位置不再关于零能对称,高度也不一致.这是由于入射角度θ越小,相应的鼓面态能量与零能偏移越大,同时自旋翻转反射峰劈裂也越大,二者的效应结合起来使不同通道的共振峰在零能左侧发生聚集,而在右侧变得疏散,因此左侧峰变高,右侧峰变低变宽.

图4 自旋电导、电荷电导与能量的依赖关系.实线表示鼓面态无色散,虚线表示鼓面态存在色散.相关参数取B=C=1 eV·nm2,λ=0.01 eV·nm,|kF|=1.1k0=1.54 nm-1,D=3 eV,a=2 meV·nm2Fig.4.Spin (charge) conductance as a function of energy with (without) drumheadlike surface states dispersion.Relevant parameters take: B=C=1 eV·nm2,λ=0.01 eV·nm,|kF|=1.1k0=1.54 nm-1,D=3 eV,a=2 meV·nm2.
4 结论
本文将节线半金属表面态的自旋输运探测方案拓展到无自旋-轨道耦合的节线半金属中.考虑到鼓面态具有较弱的色散,电子间相互作用可以诱导出表面铁磁序,从而导致界面处发生共振自旋翻转反射.该物理结果表现为自旋电导谱中的双共振峰结构.结果表明,在体能带具有自旋简并的节线半金属中,同样可以通过自旋相关输运来对其表面态进行探测;同时,自旋劈裂的表面态导致的共振自旋翻转反射,也为在该系统中对自旋进行高效操控提供了可能.
