拓扑激子绝缘体的实验进展*
2023-09-19黄月蕾单寅飞杜灵杰杜瑞瑞
黄月蕾 单寅飞 杜灵杰† 杜瑞瑞
1) (南京大学物理学院,固体微结构物理国家重点实验室,南京 210093)
2) (北京大学物理学院,量子材料科学中心,北京 100871)
电子空穴在库仑相互作用下会发生从半金属态到激子基态的相变,在费米面附近自发打开能隙,该基态被称为激子绝缘体.该物态在凝聚态物理领域吸引了广泛的关注,相关的实验证据一直在寻找中.近年来,在浅反转InAs/GaSb 量子阱中,激子绝缘体的光学能谱和输运特征首先被观察到,证实了激子绝缘体在二维体系中的存在.令人意外的是,在这一激子绝缘态中,电学输运测量探测到了对磁场和温度不敏感的一维类螺旋拓扑边缘态.这一观察到的激子基态很难用现有的单粒子理论进行解释,被称为拓扑激子绝缘体.本文系统回顾了在该量子阱中针对拓扑激子绝缘体的实验研究,包括电学输运、太赫兹透射谱、电容测量等.这些实验结果综合表征了拓扑激子绝缘体的体态与边缘态性质.拓扑激子绝缘体作为一个由玻色子构成的基态,在极限条件下有望相变为具有宏观相干性的玻色爱因斯坦凝聚态,为研究低维电子相互作用提供新的平台.
1 引言
Frenkel[1]和Wannier[2]提出,在半导体中单个电子和单个空穴可以通过库仑相互作用束缚形成激子.在20 世纪60 年代,Mott 等[3-5]进一步预测,在电子空穴共存的系统中,由于库仑相互作用,激子态会自发形成并与正常的半金属态竞争,导致系统相变为激子绝缘体.其机制类似于超导电子配对形成BCS 库珀对的过程: 在低浓度的半金属电子空穴气系统中,当温度低于与载流子浓度相关的临界温度时,电子空穴自发配对,导致半金属态能带结构不再稳定,从而打开激子BCS 能隙,因此激子绝缘体又称类BCS 激子凝聚[6].在这一温度条件下,当载流子浓度降低至极低浓度时,激子绝缘体相变为具有宏观相干性的玻色爱因斯坦凝聚体[4-11].
InAs/GaSb 反转量子阱由Kroemer 等[12,13]提出的6.1 Å家族材料构成,其带隙为负值,属于Ⅱ型异质结,具有独特的人工破缺能隙结构.如图1(a)所示,构成量子阱的InAs,GaSb,AlSb 的晶格常数均约为6.1 Å,满足晶体生长要求的晶格匹配.用AlSb 作为势垒的InAs/GaSb 量子阱中,电子和空穴带宽分别为1.35 eV 和0.41 eV.同时,因为InAs 的价带顶比GaSb 的导带底低0.15 eV,所以量子阱体系中的导带和价带有限重叠,形成反转能带(图1(c)).在实空间内,电子和空穴被分离在两层不同的相邻量子阱中,因而系统中允许p 型和n 型载流子共存,且电子空穴不容易复合湮灭,为不依赖于光激发的平衡态激子提供了一个可能的存在环境[4,13,14].此外,在InAs/GaSb 系统中,通过改变前栅极和背栅极的电压,可以分别调控电子和空穴的浓度.因此,在实验中能够同时调整能带反转程度和费米能(图1(b))[15,16].除栅压调控外,能带反转程度的调整也可以通过改变量子阱厚度实现,使得InAs/GaSb 量子阱具有高度可调性,为探索包括激子绝缘体在内的量子基态提供了一个理想的平台.

图1 (a) 6.1 Å家族材料的能带排列和每种材料的晶格常数,阴影部分表示能隙,单位为eV [12];(b) InAs/GaSb 反转量子阱的能带示意图,电子被限制在InAs 层,空穴被限制在GaSb 层,红色虚线表示空穴带顶,蓝色虚线表示电子带底,该图主要为体现材料间的能量关系,未画出界面处的能带弯曲;(c) 反转能带和非反转能带结构示意图;(d) 系统物态关于前栅压和背栅压的相图,区域I,II,III 为反转区,区域II 为费米能在体态能隙中时的量子自旋霍尔相,区域I,III 分别为p,n 型掺杂的反转体系,区域IV,V,VI 为非反转区,区域V 为费米能在体态能隙中时的普通绝缘体,区域IV,VI 分别为p,n 型掺杂的普通半导体[17];(e) 反转能带下不同电子空穴浓度时的相图,远离电荷中性点(charge neutral point,CNP),系统表现为p 型掺杂(p-doped)或n 型掺杂(n-doped),电荷中性点附近,高载流子浓度时系统为量子自旋霍尔绝缘体(quantum spin Hall insulator,QSHI),低浓度时为拓扑激子绝缘体(topological exciton insulator,TEI);(f) 典型的InAs/GaSb 和InAs/GaInSb 量子阱结构;(g) InAs/GaInSb 器件在不同背栅压下的电荷中性点载流子浓度;(h) InAs/GaInSb 量子阱制备的10 μm×5 μm 的霍尔型器件在不同背栅压下的Rxx-Vf 曲线;(i) 背栅压为0 V 时,InAs/GaInSb 量子阱制备的3 μm×1.5 μm 霍尔型器件在不同垂直磁场下的Rxx-Vf 曲线,插图为RCNP-B⊥曲线[24]Fig.1.(a) Band lineups in the 6.1 Å family material and the lattice constants of each material,the shaded parts show the energy gaps with all energies in eV[12];(b) the band diagram of inverted InAs/GaSb quantum wells,the electrons are confined in InAs layer,and the holes are confined in GaSb layer,the red dashed line indicates the top of hole band,while the blue dashed line indicates the bottom of electron band,the figure mainly reflects the energy relationship between materials,and the energy bending at the interface is not showed;(c) schematic of inverted and non-inverted band structures;(d) the phase diagram for different front (Vf) and back (Vb) gate voltages.Regions I,II,III are in the inverted regime,in which the striped region II is the quantum spin Hall phase with the Fermi-level in the bulk gap,and I,III are the p-doped and n-doped inverted system.Regions IV,V,VI are in the normal regime,in which the striped region V is the insulating phase with the Fermi level in the bulk gap,and IV,VI are the p-doped and n-doped normal semiconductors[17];(e) the phase diagram for electron and hole densities in the inverted band structure.Away from the charge neutral point,the system is p-doped or n-doped,near the charge neutral point,the system is a quantum spin Hall insulator at high charge densities and a topological exciton insulator at low charge densities;(f) typical InAs/GaSb and InAs/GaInSb wafer structures;(g) the charge neutral point density vs.back gate voltage traces in the InAs/GaInSb device;(h) Rxx vs.Vf traces measured from a 10 μm×5 μm Hall bar of InAs/GaInSb quantum wells under different back gate voltages;(i) Rxx vs.Vf traces measured from a 3 μm×1.5 μm Hall bar of InAs/GaInSb quantum wells under different perpendicular magnetic fields at Vb=0 V.Inset: RCNP vs.B⊥ trace[24].
半金属系统中,电子和空穴同时存在,由于库仑相互作用和量子隧穿等效应,体系可能演化为不同的基态.一方面,InAs/GaSb 量子阱中电子空穴的隧穿会产生杂化能隙,载流子浓度越高,杂化能隙越大.此外,高载流子浓度还会屏蔽库仑相互作用,不利于激子的形成.所以在高浓度的深反转InAs/GaSb 量子阱中,隧穿效应导致的杂化能隙在系统中占据主导.此时InAs/GaSb 量子阱可能为具有螺旋边缘态的量子自旋霍尔绝缘体(图1(d)),受时间反演对称性保护[17-21].在InAs/GaSb 体系的实验中,文献[22,23]通过输运手段探测到拓扑边缘态信号,但因为杂化能隙较小,所以边缘态信号混合了导电的体态信号.通过将GaSb 替换为GaInSb 合金(图1(f)右),量子阱的杂化能隙扩大到~20 meV,体态绝缘性提高[24].在InAs/GaInSb量子阱制备的霍尔型器件中,当通过栅压调控将电荷中性点调至~2×1011cm-2时(图1(g)),观测到了来自边缘态的Rxx峰,峰值与Landauer-Buttiker公式描述的量子化数值一致[25,26].如图1(h)所示,随栅压升高,Rxx峰值逐渐上升,偏离量子化值,表明边缘态的相干长度减小.此外,量子化的电阻峰值表现出明显的磁场依赖性(图1(i)): 随磁场增强,Rxx峰值上升.该现象可归因为外加磁场破坏了系统的时间反演对称性,导致边缘态间的背散射增加.以上输运特征说明深反转InAs/GaSb 量子阱中观测到的边缘态来源于杂化能隙导致的量子自旋霍尔效应(QSHE),对应图1(e)中的量子自旋霍尔绝缘体(QSHI)区域.
另一方面,在InAs/GaSb 量子阱中,通过栅压调节能带,可以使得能带从深反转变为浅反转.对于浅反转的InAs/GaSb 量子阱,在电子空穴浓度相近的时候,载流子浓度可以比能带深反转时更低.此时电子间的屏蔽效应随浓度降低而减弱,库仑相互作用将占据主导.同时,由于载流子浓度低,杂化能隙也进一步减小.在这种情况下,体系中杂化能隙导致的QSHE 将不再作为主要效应,可以期望观测到自发形成的激子基态,如激子绝缘体(图1(e)).如下文所述,在InAs/GaSb 量子阱中,光学和输运等实验结果揭示了激子绝缘态中体态的BCS 能隙,提供了激子绝缘体存在的明确的实验证据.此外,输运测量还意外观测到了该系统具有拓扑边缘态.自20 世纪60 年代激子绝缘体理论提出以来,该物态一直被认为是拓扑平庸的,即不存在拓扑边缘态.而在InAs/GaSb 量子阱中被观察到的这一物态,是一个体态由激子BCS 能隙主导且存在着时间反演对称性破缺的一维类螺旋边缘态的激子基态,很难用传统的激子绝缘体和单粒子图像下的拓扑绝缘体理论解释,从实验现象出发,这一物态被称为拓扑激子绝缘体[27,28].
2 激子绝缘相体态
图2(a)—(d) 展示了一系列输运实验结果,通过在低磁场下测量具有非对称电极的InAs/GaSb霍尔型器件,对比了量子自旋霍尔效应和拓扑激子绝缘体的B/(eRxy)(载流子浓度)和栅压的关系.图2(a),(b)分别对应能带深反转(杂化能隙占主导)和能带浅反转(激子绝缘体能隙占主导).在图2(c),(d)中,区域Ⅰ和Ⅳ是电子和空穴主导区,载流子浓度与栅压ΔVf呈线性相关.当费米面从电子主导区(区域Ⅰ)下降至空穴顶时,系统进入区域Ⅱ对应的电子空穴共存区,此时B/(eRxy)曲线发散(图2(a),(b)).图2(c)中区域Ⅲ的虚线表示电子空穴隧穿形成的杂化能隙中的剩余载流子.此时体能隙较小,体态仍由剩余的电子和空穴载流子主导,导致杂化能隙中的态密度较高.而对于激子绝缘体,当接近电荷中性点时,载流子浓度极低(<1011cm-2),形成了单粒子模型中不存在的激子能隙,输运结果中表现为B/(eRxy)的发散曲线迅速坍塌收敛,并表现出区域Ⅴ的新的平台特征(图2(e)).

图2 (a)—(d) 50 μm×50 μm 非对称霍尔型器件的输运测量;(a),(b) Vb=0 V 和-6 V 时B/(eRxy)随ΔVf 的变化,该数据在300 mK、外加1 T 垂直磁场的条件下采集;(c),(d)分别为(a),(b)对应的能带,红色区域I 为电子主导区,蓝色区域IV 为空穴主导区,绿色区域II 为电子空穴共存区,浅绿色区域III 为杂化能隙,虚线表示杂化能隙中剩余的电子和空穴,金色区域V 为激子绝缘体能隙,插图为非对称霍尔型器件示意图,虚线框内为前栅区域;(e) 电荷中性点处的载流子浓度随背栅压的变化;(f) 在B∥为0/9/18/35 T 时,经典反转能带中隧穿电子和空穴的色散关系,计算采用8 能带自洽模型;(g) Corbino 测量装置示意图;(h) 在温度为30 mK,平行磁场分别为0 T 和35 T 时,不同载流子浓度的电导σxx-ΔVf 曲线,载流子浓度n0 的单位为1010 cm-2;(i) Vb=0 V 时,不同平行磁场下的能隙Δ,误差提取自Arrhenius 图中能隙的不确定度,插图35 T 时σxx 极小值的Arrhenius 图,虚线为辅助线[6]Fig.2.(a)-(d) Magneto-transport in an asymmetric 50 μm × 50 μm Hall bar device;(a),(b),B/(eRxy) versus ΔVf for Vb=0 and-6 V,respectively,the data were taken at 300 mK with a 1 T perpendicular magnetic field;(c),(d) show band alignments corresponding to (a),(b),respectively,the red regime I is the electron dominating regime,the blue regime IV is the hole dominating regime,the green regime II is the electron-hole coexisting regime,the light green regime III is the soft gap,the dotted line means residual electron and hole filling in hybridization gap,the gold regime V is the hard gap (excitonic insulator gap),inset is the schematic of the asymmetric Hallbar,and the region in the dashed box is covered by the front gate;(e) charge neutral point density as a function of back gate bias;(f) energy dispersions calculated with an 8-band self-consistent model for tunneling electrons and holes with a typical inverted band at B∥=0,9,18,35 T;(g) schematic of the Corbino measurement;(h) density-dependent σxx-ΔVf traces under 0 T and 35 T in-plane magnetic fields at 30 mK,the value of n0 is noted in units of 1010 cm-2;(i) gap energy Δ vs. B∥trace at zero back-gate bias,the error bars come from the uncertainty in extraction of gap energy from Arrhenius plot.Inset is Arrhenius plot of the conductance minimum σxx at 35 T.Dashed line is a guide to the eye[6].
由于量子自旋霍尔绝缘体和拓扑激子绝缘体均存在体态能隙,因此需要对电输运测量中观测到的绝缘态成因进行分析,施加平行面内磁场可以区分隧穿杂化和激子对能隙的贡献[29].在单粒子图像中(图2(f)),具有相同动量的电子和空穴的隧穿形成杂化能隙.外加平行面内磁场会使得隧穿的粒子获得额外的动量,从而引起价带和导带的相对移动,导致电子空穴动量失配,层间隧穿被抑制.根据8 能带自洽计算,当磁场强度超过18 T 时,导带和价带在动量空间完全分离,系统变为半金属态,此时在输运测量中可以期待观测到系统从绝缘态变为导电态[6].与之相反,库仑相互作用导致的激子能隙不会被平行磁场所影响.实验中用Corbino器件来专门测量样品的体态特性(图2(g)).Corbino器件为同心圆结构,内外分别有金属触点,用于连接二维电子气,构成电流回路.同时,器件中的边缘态电流会被同心的金属结构短路,只能探测到体态电导,因此测量Corbino 可以获得体态能隙的直接信息.实验结果如图2(h)所示,在InAs/GaSb器件中,当背栅压Vb为-6 V 时,载流子浓度为1011cm-2,说明此时能带深反转.在磁场为0 T 时,电荷中性点处观测到由于杂化能隙带来的电导极小值,当平行磁场加强至35 T,该电导极小信号快速消失,说明在平行磁场作用下,杂化能隙被半金属态取代.随着Vb上升,中性点附近载流子浓度减小,电导极小信号减小,且对应的前栅压宽度增大,此外施加的平行磁场对电导极小信号的影响逐步减弱,表明和杂化能隙竞争的激子能隙逐渐增强,并最终在系统中占主导.当Vb=0 V 时,中性点附近载流子浓度减小为5.5×1010cm-2,此时能带浅反转,0 T 与35 T 平行磁场下的电导极小信号几乎保持不变,这说明在极大的平行磁场下,体态能隙也没有被闭合.进一步的热激发输运测量实验中,在Vb=0 V 时,根据σxx ∝exp(-Δ/2kbT)可以确定,在0—35 T 的平行面内磁场下,体态能隙始终保持~2 meV (~25 K)(图2(i)).这些结果证明了在浅反转区域能隙的主要成因不是电子空穴隧穿导致的能带杂化,而是库仑相互作用下电子空穴配对形成了激子.
为进一步分析能隙成因,实验中在Vb=0 V 时对激子绝缘体样品进行了太赫兹透射谱研究[30-32].根据平均场理论,可以计算出激子绝缘体的BCS能隙的对破缺激发谱E(k)和能隙函数Δ(图3(a)),分析后得到图3(b)的联合态密度.联合态密度谱计算说明激子绝缘体的BCS 能隙存在两个吸收峰,能量分别约为1.5 meV 和7 meV,其中7 meV由两个靠近的吸收峰构成.如图3(c)所示,在实验中太赫兹透射谱探测到了两个信号峰A(~2 meV)和B(~7.3 meV).虽然量子阱中的电势波动导致信号峰存在一定程度的展宽[33],但探测到的两个信号与计算结果定量一致.同时,吸收峰A 的能量也与通过热激发测量确定的激发能(~2 meV)非常接近.这一能谱信息无法用该系统中的单粒子杂化能隙图像解释[17],给出了浅反转InAs/GaSb 量子阱中存在激子绝缘体能隙的直接证据.太赫兹透射谱的温度依赖性实验显示(图3(d)),在温度低于10 K 时,A,B 两个吸收峰始终存在;随着温度上升,谱线的吸收强度显著降低,在10 K 以上时,A,B双线结构完全消失,说明在高温下,热扰动导致激子不稳定,分解成为电子空穴气(等离子体).因为太赫兹透射谱线的吸收强度与联合态密度正相关,所以吸收峰的温度依赖性直观反映了系统在临界温度(~10 K)附近,由激子绝缘体到电子空穴等离子体的相变过程,同样证明了该信号来源于激子绝缘体的BCS 能隙.此外实验中发现,在低温下对样品施加垂直于量子阱平面的磁场时,A,B 信号峰强度增加,同时B 线出现轻微蓝移(图3(e)).在高温下(20 K),外加磁场使得原本在0 T 时消失的信号峰重新出现,且垂直磁场诱发的信号蓝移效果增强(图3(f)).这说明垂直磁场增强了电子空穴间的束缚,使激子对更加稳定,从而抑制了热扰动效应导致的激子分解[9,34-36].A,B 谱线虽然能量不同,但对温度和磁场具有相同的依赖性和特征,证明了这两个信号峰均来源于激子绝缘体相变的过程,且分别对应从激子的基态到具有不同动量k末态的过程.
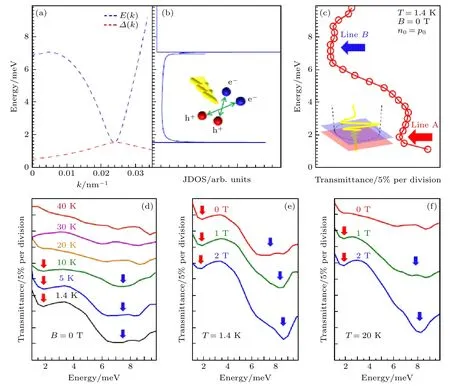
图3 激子绝缘体的激子对破缺能谱和太赫兹透射实验 (a) Vb=0 V 时,激子关于波矢k 的能隙函数Δ(k)(红色虚线)和对破缺能量E(k)(蓝色虚线);(b) 联合态密度(JDOS)关于能量E 的函数,插图为太赫兹激光诱发的激子对破缺(蓝点表示电子,红点表示空穴,黄色箭头表示太赫兹入射光);(c) Vb=0 V 时,在1.4 K,0 T 的电荷中性点处的太赫兹透射谱,插图为紫色层为InAs 量子阱,红色层为GaSb 量子阱,黄色波浪线为太赫兹激光,黑色虚线表示太赫兹入射光在样品上聚焦时的横向范围;(d) 0 T时,不同温度下的透射谱;(e),(f) 1.4 K 和20 K 时,不同磁场下的透射谱,光谱在垂直方向上平移,太赫兹能谱的测量误差为±0.2 meV[6]Fig.3.Pair-breaking excitation spectra and Terahertz transmission spectrum of excitonic insulator: (a) Gap function Δ(k) (red dashed line) and the pair-breaking energy E(k) (blue dashed line) of the exciton as a function of k for Vb=0 V;(b) joint density of states (JDOS) as a function of energy.Inset: Pair-breaking induced by THz light (Blue dots are electrons,red dots are holes,yellow arrow is THz light);(c) transmission spectrum at the CNP at 1.4 K and 0 T for Vb=0 V (Inset: The purple layer represents the InAs quantum well,the red layer represents the GaSb quantum well,the yellow wave indicates the THz light,the dashed black circle marks the lateral extent of the focused THz beam at the sample position);(d) transmittance spectra at various temperatures at 0 T;(e),(f) transmittance spectra at different magnetic fields at 1.4 and 20 K,respectively,the spectra are vertically offset for clarity,the measurement uncertainty in THz energy is ±0.2 meV[6].
随后,在电容测量中,激子绝缘体的体态能隙被进一步研究.受到安德森局域化的影响,电导测量的能隙结果可能存在偏差,而电容测量可以通过器件的电容值直接给出系统的态密度信息.态密度的减小对应着能隙的打开.相关测量电路如图4(a)所示,通过向前栅施加直流偏置电压(调节载流子浓度)和低频率(~100 Hz)的小交流电压,可以得到前栅与量子阱间的电容Cm=dQ/dV.这一容值由样品几何电容Cg和量子电容Cq串联形成.其中,几何电容可以通过分析器件结构得到,而量子电容和体态态密度成正比.图4(c)中深反转和浅反转能带的电容测量结果展示了能隙附近态密度的变化.在能带深反转时(蓝线),杂化能隙占主导,能隙 (ΔVf=0 V)处的电容特征与电荷/空穴主导区(|ΔVf|>0.5 V)相似,容值没有出现明显下降,表明此时量子阱层间隧穿太弱,能隙中由电子和空穴贡献的态密度较大,没有形成绝缘体.这也与文献[29]的杂化能隙结果一致.形成鲜明对比的是,在能带浅反转时(红线),激子能隙导致的电容相比电荷/空穴主导区的容值迅速下降了90%,充分证明了此时体态态密度减小.而体态电子空穴态密度的减小是由于在低载流子浓度下电子空穴形成了激子对,不再贡献态密度.在电容测量中改变温度(图4(d)),激子能隙的电容信号下降幅度随温度上升逐渐减小,并最终在10 K 完全消失.这说明高温下热激发使得激子绝缘体不稳定,分解变成电子空穴等离子体,导致能隙中态密度的上升和电容信号的增加.根据不同温度下的能隙处的电容,可以得到激子能隙对温度的依赖关系,这一结果与激子绝缘体BCS 能隙的理论计算(图4(e)虚线)符合良好.能隙在5 K 时开始减小,并且在激子绝缘相的临界温度(~10 K)消失,这一结果也与前文中的太赫兹透射谱和电输运结果一致.
通过调控背栅压,实验中进一步研究了激子绝缘体能隙对载流子浓度的依赖关系.背栅压从0 V调至-6 V 的过程中,载流子浓度逐渐增大,通过热激发测量到的激子绝缘体能隙逐步减小.这证明了随着载流子浓度上升,粒子间的屏蔽效应随之增强,电子空穴间的束缚减弱,因此激子绝缘体不再稳定,表现为能隙减小(图5(a),(b)).另一方面,在垂直磁场作用下,体态在激子绝缘体区域始终是完全绝缘的.随着磁场升高,激子能隙增大,从0 T的26 K 上升至6 T 时的40 K(图5(c),(d)),同样与太赫兹实验结果符合.
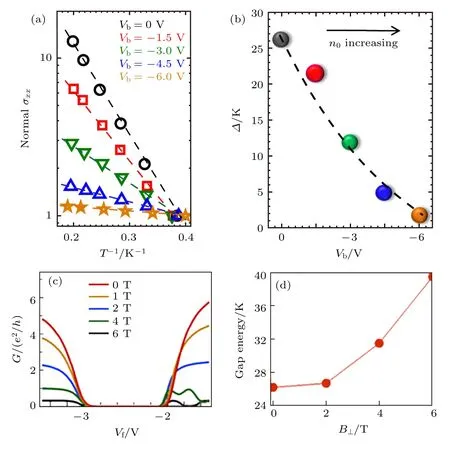
图5 体态电导对背栅压和垂直磁场的依赖性 (a) 不同背栅压时电导最小值的Arrhenius 图,根据σxx ∝ exp(-Δ/2kBT)拟合得到Δ;图中σxx 根据2.5 K 处的值归一化,虚线为辅助线;(b) 能隙Δ-Vb[6];(c) 300 mK 时,Corbino 器件在垂直磁场下测量到的电导G-Vf 曲线;(d) G-B⊥曲线[37]Fig.5.Dependence of bulk conductance on back gate bias and perpendicular magnetic fields: (a) Arrhenius plot of the conductance minimum for different back-gate bias voltages,the data can be fit by σxx ∝ exp(-Δ/2kBT) to obtain Δ,here the σxx is normalized by its value at 2.5 K,dashed lines are guides to the eye;(b) measured gap energy Δ vs.Vb trace[6];(c) G vs.Vf traces measured in Corbino device at T=300 mK under perpendicular magnetic fields;(d) G vs.B⊥ traces[37].
3 拓扑边缘态
自激子绝缘体这一概念提出以来,科学界广泛认为其是拓扑性质平庸的.但在近年的实验中,我们意外地发现,在浅反转InAs/GaSb 量子阱中,当费米能被调至激子绝缘能隙时,样品的边缘存在着一维无能隙的类螺旋拓扑边缘态,即手性相反的具有线性色散的一对拓扑边缘态[37].通过对拓扑激子绝缘体的介观器件进行输运测量,可以有效探测其边缘态.图6(a)显示了介观π 型和霍尔型器件的输运结果.在激子绝缘体能隙处测量到的电导具有精确的量子化值,与理论值相比,误差约为1%.通过对电导量子化数值使用Landauer-Buttiker 公式进行分析可以发现[25,26],其电导是由一维类螺旋拓扑边缘态产生的[27,28].并且该量子化电导在很大的前栅压范围中均存在,表现出平台特征.在不同几何结构(如π 型、霍尔型及两端结型器件)的非局域测量中,这一现象均被观测到,且电导平台可以量子化到不同的数值(图6(a),(d)),其数值和Landauer-Buttiker 公式针对螺旋拓扑输运的计算结果符合.与之形成鲜明对比的是,在非反转的InAs/GaSb 量子阱霍尔型器件的输运实验中,并没有探测到量子化的信号(图6(b)).相反,在电荷中性点附近出现了来自体态非反转能隙的绝缘信号,这充分说明了在非反转的InAs/GaSb 量子阱中并不存在边缘态.而在浅反转InAs/GaSb 量子阱中观测到的一维边缘态和系统的拓扑性质有着紧密联系.

图6 介观器件中的拓扑边缘态输运 (a) 在1 μm×2 μm 的霍尔型器件和π 型器件中,分别测到量子化为2e2/h 和4e2/h 的宽电导平台,插图为平台在温度低于4 K 时保持稳定;(b) 在300 mK,0 T 时,非反转量子阱的10 μm×20 μm 霍尔器件中测得的Rxx-ΔVf 曲线,插图为非反转能带示意图;(c) 不同边缘长度的器件中的边缘电荷输运,插图为不同温度下的Rxx-L 曲线;(d) 在1 μm×1 μm 两端结器件、1 μm×1 μm 和1 μm×2 μm π 型器件、1 μm×2 μm、5 μm×10 μm 和10 μm×20 μm 霍尔型器件中,Rxx-L 曲线;(e),(f) 测量4 种不同结构的器件的边缘态对磁场的依赖性,对器件分别施加(e) 磁场方向平行(空心圆形)或垂直(空心三角形)于边缘轴向的平行面内磁场,(f) 垂直于量子阱平面的磁场[37]Fig.6.Topological edge transport in mesoscopic devices: (a) Wide conductance plateaus in 1 μm×2 μm Hallbar and π bar quantized to 2e2/h and 4e2/h,respectively (Inset: Plateau persists to 4 K);(b) measured Rxx vs.ΔVf trace in a 10 μm × 20 μm Hall bar from the noninverted quantum wells at 300 mK and 0 T (Inset: A sketch of noninverted band);(c) electrical charge transport in devices with different edge lengths (Inset: Rxx vs.device edge length L traces under different temperature);(d) Rxx vs.device edge length L traces in 1μm×1μm junction,1 μm×1 μm and 1 μm×2 μm π bars,1 μm×2 μm,5 μm×10 μm and 10 μm×20 μm Hall bars;(e),(f) dependence of edge states under high magnetic fields in four different kinds of devices,an in-plane magnetic field (e) with a direction parallel (open circles) or perpendicular (open triangulars) to the edge axis and a perpendicular magnetic field (f) is applied to the device,respectively[37].
对于平庸电子态,其电阻值始终与器件长度呈线性相关;而在拓扑激子绝缘体中,虽然边缘态电阻一开始随器件长度减小而降低,但当长度小于一定值时,阻值不再随器件长度而减小,而是始终保持恒定的量子化值(图6(d)).该长度临界值即为相干长度λ.对于长度为L的器件,当L小于λ时,边缘态受到拓扑保护,此时阻值与器件长度无关,系统表现出弹道输运特征;而当L大于λ时,拓扑边缘态在相干长度内发生弹道输运,但在相干长度处电子会发生背散射,所以边缘态可近似为N个量子电阻的串联(N~L/λ),器件总电阻值为(L/λ)·h/(2e2).在实验中,通过测量不同尺寸的浅反转InAs/GaSb 量子阱霍尔型器件,分析得到该样品的相干长度为λ~4.4 μm.且在输运测量中,当温度在4.2 K 以下时,在该系统中均测量到量子化电导和相干长度的特征信号(图6(d)).
对浅反转的InAs/GaSb 量子阱器件施加平行面内磁场,场强由0 T 上升至12 T 的过程中,不论磁场平行或垂直于边缘态,量子化电导平台信号始终保持稳健(图6(e)).表明拓扑激子绝缘体的边缘态不受平行磁场干扰,说明系统的时间反演对称性是破缺的,这一点与量子自旋霍尔绝缘体有着显著的区别[25,26].图6(f)中,在垂直于量子阱平面的磁场作用下,π 型器件和霍尔型器件的纵向电导上升,而两端结型器件的电导下降.在垂直磁场作用下,洛伦兹力会导致拓扑边缘态的两个不同手性的传播通道分别朝器件内外移动,即一个通道朝器件边缘扩张,另一个朝器件内部收缩.因此,边缘态通道在实空间分离,导致通道间的背散射减小.根据Landauer-Buttiker 公式,背散射减小会导致纵向电导增大,霍尔电导减小[25].而在垂直磁场下,由Landauer-Buttiker 公式可知,两端结型器件电导反映的是霍尔信号,π 型和霍尔型器件的纵向电导反映了纵向信号.这就解释了实验中观察到的边缘态行为,证明边缘态在垂直磁场下仍然存在,同时也说明浅反转能带下的边缘态是由一对手性相反的一维通道构成.垂直磁场的实验给出了拓扑激子绝缘体拓扑边缘态内部精细结构的实验迹象.可以期待的是,如果磁场进一步增强,激子对的电子空穴距离会继续增大,从而只有向外扩张的传播通道会被电极探测到,而向内收缩的传播通道对于电极则是“隐身”的.在这种情况下,边缘态的输运现象将会由零磁场时的类螺旋输运转变为类似于ν=1 的量子霍尔效应的手性输运,出现新的量子化平台特征.需要指出的是,虽然浅反转InAs/GaSb量子阱中量子化的边缘态在磁场下的行为与HgTe量子阱中的量子自旋霍尔效应完全相反[38],但该边缘态的实验结果一开始被解释为量子自旋霍尔效应.根据前文第2 节中对该量子态的实验回顾可知,其体态由BCS 激子能隙主导,而非能够导致量子自旋霍尔效应的杂化能隙,所以被观察到的量子化边缘态并非来自于量子自旋霍尔效应.现有的理论模型尚未完全解释拓扑激子绝缘体中的实验现象[27,39-54],相关的理论研究仍然有待推进.
实验方面,为了分析拓扑边缘态的性质,对拓扑激子绝缘体的一维类螺旋边缘态进行了一维库仑拖曳实验[55].一维库仑拖曳是指,一根导线中的电流通过库仑相互作用,在相距纳米尺度的第二根导线中产生感应电压[56-67].根据拖曳信号的不同,分为正库仑拖曳[61,64,65]和负库仑拖曳[62-64](图7(a),(b)).具有线性色散能带的边缘态间的自旋翻转相互作用会导致边缘态中存在直接背散射和反转背散射.前者为动量匹配的相邻螺旋边缘态之间的库仑散射,与正库仑拖曳相关;后者发生于具有相反动量的两个边缘态之间,与负库仑拖曳相关[68-70].当存在驱动电流时,两种拖曳机制同时生效,对净拖曳信号做出贡献.根据一维库仑拖曳理论,在两个理想的一维导电通道系统中,电子空穴对称性会使得狄拉克点处的正负库仑拖曳信号相互抵消,因此净拖曳信号为零[69].但由于真实系统中总是存在势能波动,使得费米能在局部区域偏离狄拉克点,从而加强反转背散射,使拖曳电流倾向于负库仑拖曳.这一机制在狄拉克点附近尤其明显,并且这一波动对低载流子浓度的系统影响更大.在InAs/GaSb 量子阱中,能带浅反转时存在拓扑激子绝缘体,而此时电荷中性点附近载流子浓度极低(<1011cm-2),因而在狄拉克点处对负库仑拖曳更为敏感.

图7 (a),(b) 正和负库仑拖曳,红线和蓝线分别表示手性相反的边缘态;(c) 劈裂的H 器件中,有源驱动电路和拖曳电路的示意图,驱动电路中,电极3 注入电流,电极1 接地.拖曳电路中,测量电极2 与4 间的电压.绿框内为库仑拖曳的关键部分.插图:H 器件中间劈裂的空气间隙的扫描电子显微镜成像,比例尺为100 nm;(d) 相邻两个边缘态的线性色散关系,费米能在狄拉克点附近;(e),(f) 负和正库仑拖曳的净电流流向示意图,虚线表示净电流方向,驱动电路的设置与(c)一致[47]Fig.7.Positive (a) and negative (b) Coulomb drags,red and blue lines denote edge states with opposite chirality;(c) schematic of active drive circuit and drag circuit in a split H-bar,a current is injected into contact 3 with contact 1 grounded,and a voltage between contacts 2 and 4 is measured,the active part for Coulomb drag is highlighted by a green box (Inset: Scanning electron micrograph of the air gap in a split H-bar,scale bar is for 100 nm);(d) linearly dispersing energy band structures of two neighboring edges with the Fermi level around the Dirac point;(e),(f) current flow of the negative and positive drag,dashed lines show the current flow,the current is injected into the drive circuit in the same way as in (c)[47].
为了观测一维类螺旋边缘态间的库仑拖曳,我们在实验中制备了H 型介观器件,并在器件中间劈裂~50 nm 宽的空隙(图7(c)),使两侧边缘态被空隙隔开.由于库仑相互作用与介电常数成反比,真空的低介电常数可以有效提高拖曳与驱动电流间的相互作用,加强两支边缘态的横向耦合.在驱动电流的感应下,边缘态会在拖曳回路中形成稳态电流.在输运测量中,这一感应信号表现为在拖曳回路的测量电极探测到非零的拖曳电压(图7(e),(f)).因为拖曳电压Vdrag和拖曳电流Idrag成正比,为了表征拖曳信号强度,定义拖曳电阻Rd=-Vdrag/Idrive.在图8(a)—(d)中,当前栅压调节费米能至激子能隙时,ΔVf~0,探测到有限的拖曳电阻,表明非局域的拓扑边缘态在系统中占主导;当ΔVf≥1.5 V 时,费米面远离激子能隙,此时驱动回路和拖曳回路中均不存在边缘态,拖曳电阻在零附近波动,表明此时不存在拖曳电流.因为分析目标是边缘态的性质,所以主要关注激子能隙处(ΔVf~0)的信号.图8(e)中300 mK 时,激子能隙处拖曳电阻为负值,表明负库仑拖曳机制占主导.在温度不高于1 K 时,拖曳电阻始终为负,且随温度上升而减弱,表现出单调的温度依赖性.在1.2—1.3 K 附近,拖曳电阻为正值,且出现极值,说明此时正库仑拖曳贡献更大.当高于1.5 K 时,库仑拖曳信号基本消失.变温库仑拖曳实验结果证明,当系统费米能的平均值在狄拉克点(电荷中性点)时,局部区域的费米能实际已偏离狄拉克点(即在局部区域的电子空穴浓度并不平衡),且在低温下,该偏离克服了热效应导致的波动,使得反转背散射机制占主导.而当温度上升,在非理想的真实系统中,局部区域费米能相对狄拉克点的偏离被增强的热展宽效应所抑制,此时可以认为系统费米能处在狄拉克点.由于狄拉克点的对称性,直接背散射增强至与反转背散射相当的强度,使得两种散射机制达到平衡.图8(f)基于文献[70],定性描述了两种机制的温度依赖性.结合输运实验中已经证实的在2 K甚至更高温度时系统中仍然存在边缘态,可以确认在较高温度下拖曳信号的消失是因为相邻一维边缘态之间的相互作用被屏蔽,即不同的拖曳机制在较高的温度下竞争并相互抵消.一维库仑拖曳实验结果证明了拓扑激子绝缘体的一维边缘态存在着狄拉克点.

图8 拓扑边缘态间的库仑拖曳信号对前栅压和温度的依赖性 在300 mK (a),1 K (b),1.5 K (c) 和2 K (d)下,劈裂的H 器件中边缘态的拖曳电阻随前栅压的变化,将电阻信号最强处设为ΔVf=0 V,紫色阴影表示激子绝缘体区(插图(i)和(ii)分别描述了直接背散射和反转背散射机制),蓝色和红色线对应具有线性色散关系的狄拉克能带,实心/空心圆分别表示散射过程中的初始/最终状态;(e) 样品Ⅰ(蓝色)和样品Ⅱ(红色)在电荷中性点处拖曳电阻随温度的变化;(f)正负库仑拖曳电阻与温度的定性关系,蓝绿色曲线表示反转背散射对负拖曳信号的贡献,橙色曲线表示直接背散射对正拖曳信号的贡献[47]Fig.8.Front gate voltage and temperature dependence of Coulomb drag signals in topological edges: Drag resistance of edge states vs.front-gate voltage in the split H-bar device at 300 mK (a),1 K (b),1.5 K (c) and 2 K (d),the zero front-gate voltage is set at the value for which the resistance is the largest,purple-shaded areas indicate the topological exciton insulator regime (Insets: (i) and(ii) describe the direct and umklapp backscattering mechanisms,respectively),the blue and red lines correspond to linearly dispersing Dirac bands,filled/open circles represent initial/final states in scattering,respectively;(e) temperature dependence of the drag resistance at the CNP for sample Ⅰ (blue) and sample Ⅱ(red);(f) qualitatively sketched temperature dependence of positive and negative drag resistivity,the blue-green curve indicates the contribution of negative drag from umklapp backscattering and the orange curve represents the contribution of positive drag from direct backscattering[47].
4 发展与展望
本文总结了光谱探测、输运测量和库仑拖曳等实验中,观测到的浅反转InAs/GaSb 量子阱中的拓扑激子绝缘体的特征: 1)与杂化能隙不同,体态的激子能隙不被平行磁场影响;2)太赫兹透射谱中存在具有激子BCS 能隙特征的双吸收峰;3)激子能隙的电容随温度降低而减小,该温度依赖关系满足BCS 能隙理论计算;4)零磁场下存在着一维的线性色散类螺旋边缘态;5)该边缘态存在量子化的平台,平台宽度显著大于普通能隙;6)该边缘态在4.2 K 以下对温度不敏感;7)该系统具有时间反演对称性破缺的特征,边缘态不会被磁场破坏,在垂直磁场下,螺旋边缘态的两个传播通道会被分离;8)形成拓扑激子绝缘体时,局部区域的电子空穴浓度不相等.所以这一拓扑激子绝缘体的体态由激子的BCS 能隙主导且粒子空穴浓度不等,其边缘存在着时间反演对称性破缺的一维类螺旋态.目前为止,InAs/GaSb 实验中观测发现的这种物态还无法被现有的激子绝缘体和单粒子拓扑绝缘体理论所解释[27,39-54],说明这是一个全新的量子物态.InAs/GaSb 系统中电子空穴在实空间分离的独特性质,为深入研究无光泵浦平衡电子空穴系统中的激子平衡态提供了良好的平台.实验上,一方面,通过继续提升磁场强度,能够进一步验证浅反转InAs/GaSb 系统中边缘态的精细结构.另一方面,当载流子浓度趋向极低时,平衡态激子系统很有可能表现出BCS-BEC 交叉甚至BEC 特征.此外,在其他二维系统,如石墨烯、过渡金属硫化物中,同样可以期待观测到相关激子绝缘体的性质[71-76].
