基于BSO-BP 神经网络的吸能盒多道次拉深系数优选方法研究＊

2023-09-18赵洪林赵永顺李冬芳董月厚冯金元

制造技术与机床 2023年9期

赵洪林李宁赵永顺李冬芳董月厚冯金元

（①天津翔铄车身科技有限公司，天津 301600；②天津丰通晟源科技有限公司，天津 301600；③天津丰通申易模具有限公司，天津 301600）

21 世纪以来，随着我国工业、经济水平的不断提高，汽车保有量也得到了跨越式增长。2022 年8月数据显示，我国汽车保有量达到4.08 亿辆。然而在汽车工业迅猛发展的背后，汽车所带来的隐患也越来越凸显，尤其是汽车引发的交通事故更是危害公共安全的重要因素。

吸能盒是汽车保险杠系统中重要的吸能装置，可吸收车辆与车辆、车辆与行人碰撞过程中产生的能量，有效降低碰撞力对车辆和行人造成的损害程度。吸能盒通常为金属制品，高径比大，行业内普遍采用多道次拉深工艺生产。然而多道次拉深成形过程中，材料受力较为复杂，涉及摩擦、接触、塑性等多重非线性耦合，理论和实际问题比一次拉深复杂。

针对多道次拉深制品的工艺优化问题，诸多学者开展了很多富有成效的研究。黄珍媛等[1]根据均匀变形和K 值法结合有限元分析技术确定了每道次制品的过渡形状并制定出了3 道次拉深工艺方案；肖冰娥等[2]以大高径比H68 铜套为研究对象，结合经验设计与数值模拟发现压边圈与凸模间隙对成形过程有很大影响，据此制定了优化的工艺与模具，得到了合格的零件；成波[3]利用Autoform 软件对各道次拉深工序进行成形模拟，优化了拉深凹模的圆角半径，经实际生产获得了满足壁厚要求的筒形件；胡开元等[4]基于响应面法和灰狼优化算法优化了H70 黄铜壳体拉深模具的凹模尺寸参数，试验结果显示制品所有尺寸指标均满足设计要求；张在房等[5]采用克里金插值法和径向基函数构建了贮箱箱底多道次成形工艺参数和质量指标之间的近似模型，利用NSGA-III 算法和粒子群算法获得了压边力、压边圈圆角半径等参数的最优值，最后通过实验验证了方法的有效性和结果的准确性。

上述文献中的多道次拉深成形优化对象主要针对模具间隙、凹模圆角半径、压边力、压边圈圆角半径等参数，事实上拉深系数对成形质量也会产生重大影响。拉深系数设置越小，说明拉深变化程度愈大，会使拉深件起皱、断裂或严重变薄超差；拉深系数设置越大，会增加拉深工序的道次数，影响产品生产效率。生产实际中，多道次拉深系数的确定多是工程人员在工程手册推荐的拉深系数范围内凭经验选定，未必能得到最优拉深系数。

针对上述问题，本文提出一种基于BSO-BP 神经网络的吸能盒多道次拉深系数优选方法，以期为生产实践中多道次拉深制品拉深系数的客观合理确定提供一种可供参考的新方法。

1 产品工艺性分析

某型汽车保险杠系统用吸能盒，产品结构如图1所示。为保证吸能盒的比吸能值不低于16.2 J/g，客户要求CAE 分析阶段各道次FLD 安全域占比不低于10%、成形后的吸能盒最大减薄率不超30%，不允许有开裂且吸能盒表面不能出现凹点、凸点、拉伤和划痕。吸能盒材质为DC06，板料厚度为1.1 mm，依据GB/T 228.1-2010《金属材料拉深试验第1 部分：室温试验方法》制备拉深试样。从垂直于轧制方向（90°）、平行轧制方向（0°）和45°轧制方向对DC06 进行单向拉深试验，每次试验选2 组试样以保证重复性。拉深试验得到的材料应力-应变曲线，如图2 所示。

图1 产品结构

图2 应力-应变曲线

计算相关试验数据并结合图2 可得DC06 的力学性能参数，见表1。

表1 DC06 力学性能参数

依据表1 数值，在Autoform 有限元分析软件中完成DC06 材料的定义，为后续有限元分析奠定基础。

2 拉深次数及成形工艺确定

为便于初步确定吸能盒的拉深次数，根据吸能盒的2D 图纸，将吸能盒近似为如图3 所示的有凸缘圆筒拉深近似模型，D为毛坯直径，计算公式见式（1）[6]。

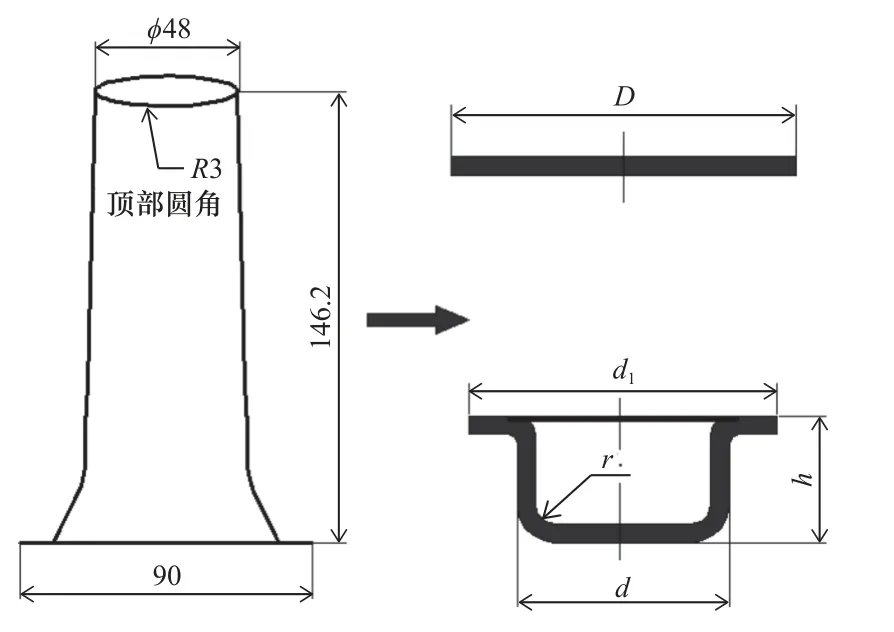
图3 吸能盒-有凸缘圆筒拉深近似模型

其中：d1=90 mm，r=3 mm，d=48 mm，h=146.2 mm，计算可得D≈188 mm。

由拉深理论可知，若总拉深系数m总大于第一次拉深系数极限值，则可一次拉深成形；反之，则需要多次拉深。m总=d/D≈0.26，毛坯相对厚度t/D×100≈0.59（t为板料厚度），查阅文献[6]可知第一次极限拉深系数为0.55～0.58，总拉深系数小于第一次极限拉深系数，因此吸能盒需多道次拉深。

为降低拉深成形过程中出现拉裂、起皱的风险，结合表1，第一次拉深系数取0.58，则第一次拉深直径为d1=m1D=0.58×188 mm≈109 mm。

拉深高度的计算公式见式（2）[6]。

式中：hi为第i次拉深高度；D为毛坯直径；ri为第i次拉深件顶部圆角；di为第i次拉深直径。

据式（2）可得第一次拉深高度h1≈60 mm。同理，依据生产经验结合文献[6]相关结论，初步确定其余拉深工序拉深系数并计算每道次工序的拉深直径和拉深高度，得到最终拉深次数为5 次，初始设计具体每道次工序拉深系数和拉深尺寸见表2。

表2 初始设计每道次工序拉深系数和拉深尺寸

前4 道次拉深为直筒拉深，第5 道次拉深为成形锥面，通常在进行成形锥面前需对第4 道次成形后的工序件进行热处理，提高其塑性。依据表2 中数据吸能盒成形工序及各工序件见图4 所示。吸能盒完整成形需9 道工序，其中OP1～OP5 为拉深工序、OP6 为底部胀形、OP7 为修边+冲上孔、OP8 为翻遍+刻印、OP9 为冲底孔。对吸能盒成形质量影响最大的工序为OP1～OP5 的拉深成形，因此本文主要针对OP1～OP5 的拉深系数的优选方法进行研究。

图4 各工序件

3 初始拉深方案CAE 分析

依据表2 中的初始拉深工艺设计方案，完成Autoform 的拉深工具体创建，各道次拉深凸凹模单边间隙统一设置为0.12 mm，摩擦系数根据现场所用润滑剂统一设置为0.15，拉深工艺参数设置采用软件默认值，得到如图5 所示的OP1～OP5 道次拉深有限元分析结果。

图5 OP1～OP5 道次拉深有限元分析结果

从图5 可以看出，OP1、OP2、OP5 道次拉深的FLD 安全域占比低于10%的要求；OP5 道次拉深的吸能盒最大减薄率超过了30%，达到40.7%，从图6 可以看出，最大减薄率区域位于吸能盒顶部圆角区域，FLD 成形极限图中出现了黑色的开裂区，开裂区占比0.49%，造成开裂的原因是材料减薄率过大，造成材料抗拉强度不足，在拉深力作用下引起材料开裂。影响板材过度减薄的因素较多，除了与拉深工艺参数设置是否合理有关外还与每道次的拉深系数的是否合理选用密切相关。本文着重探究每道次拉深系数对吸能盒拉深成形指标的影响。

图6 OP5 道次拉深厚度云图和FLD 成形极限图

4 拉丁超立方实验设计

拉丁超立方试验设计（LHD）的样本点数量可人为控制，灵活性较大。为了使拉丁超立方试验的结果具有实际意义，将OP1～OP5 道次拉深系数作为实验因素，因素水平范围在文献[6]相关论述基础上作适当调整，见表3。其中：m1为第1 道次拉深系数；m2为第2 道次拉深系数；m3为第3 道次拉深系数；m4为第4 道次拉深系数；m5为第5 道次拉深系数。

表3 OP1～OP5 拉深系数实验水平范围

根据表3 实验因素水平范围，根据拉丁超立方实验设计方法随机生成25 组实验样本，每组实验样本依据各道次拉深系数合理建立Autoform 分析工具体，拉深工艺参数设置与初始分析一致，各组实验样本对应的CAE 分析结果见表4。

表4 各组实验样本及CAE 分析结果

5 BSO-BP 神经网络建立

BP 神经网络[7]的随机初始权值和阈值使该网络不稳定，容易陷入局部最优。为了解决上述问题，引入天牛群优化算法（beetle swarm optimization，BSO），对BP 神经网络的初始权值和阈值进行优化，以进一步提高BP 神经网络预测精度。

5.1 BSO-BP 神经网络

BSO 算法[8]是一种结合了天牛觅食机制和粒子群算法的优化算法。在每一步中，都使用一组天牛进行搜索行为，每只天牛都向一个随机的方向移动，一旦出现了位置更好的天牛，全局位置最优的天牛就会逐步更新，直到BSO 找不到更好的方法，迭代过程才会完成。全局位置最优天牛是该优化问题的估计解。通过群体智力和群体认知策略，可以显著提高寻找天牛最佳位置的可能性，并使其更易达到全局搜索和局部搜索之间的平衡。BSO 基于群体认知策略的第n只天牛第t次搜索迭代模型如下[9]：

式中：δ表示天牛移动步长，f为天牛个体适应度函数，sign 为符号函数，b表示天牛移动方向；第三部分定义为群体认知部分，c2(αbest-)。个体和群体认知部分c1和c2的系数是属于[0，2]的两个随机数。左侧、右侧位置计算公式分别如式（4）、式（5）所示。

式中：d表示天牛感知长度。

综上，基于BSO-BP 神经网络的吸能盒多道次拉深系数优选流程如图7 所示[10]。

5.2 BSO-BP 神经网络建立及预测精度检验

选取OP1～OP5 道次的拉深系数作为输入变量，以吸能盒最大减薄率和FLD 安全域占比作为响应输出建立的BSO-BP 神经网络模型，模型的拓扑结构如图8 所示。

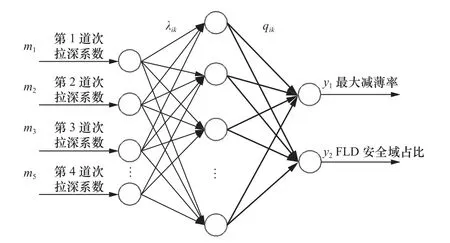
图8 BSO-BP 神经网络模型拓扑结构

为验证BSO 算法对BP 神经网络的优化效果，取表3 中的前20 组实验数据作为训练样本分别对BP 神经网络和BSO-BP 神经网络进行训练，将第21～25 号实验样本作为测试样本对二者预测精度进行检验，BP 神经网络和BSO-BP 神经网络对各组测试样本第5 道次拉深成形质量的预测结果如图9所示。

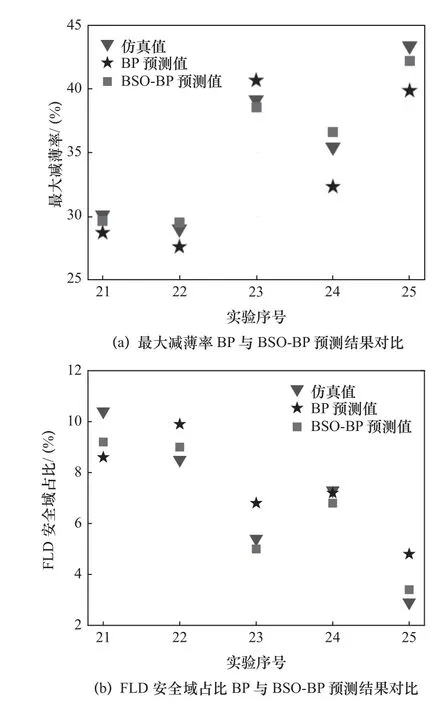
图9 成形质量BP 与BSO-BP 预测结果对比

为进一步量化比较BP 神经网络和BSO-BP 神经网络的预测以及拟合精度，以二者预测输出与期望输出之间的平均相对误差作为预测精度的评价指标；以可决系数R2作为拟合精度的评价指标比较二者性能，所得计算结果见表5。

表5 BSO-BP 与BP 性能评价

由图9 并结合表5 可以看出，BP 神经网络对于最大减薄率的预测相对误差平均值为5.58%，BSO-BP 神经网络的预测相对误差平均值为3.34%，预测精度相较于BP 神经网络提升了40.14%；经BSO 算法对BP 神经网络的权值和阈值优化后，BP神经网络的可决系数由0.930 9 增至0.993 8，更加接近于1，模型拟合精度得以显著提高。BP 神经网络对于FLD 安全域占比的预测相对误差平均值为8.54%，BSO-BP 神经网络的预测相对误差平均值为4.32%，预测精度相较于BP 神经网络提升了49.41%；经BSO 算法对BP 神经网络的权值和阈值优化后，BP 神经网络的可决系数由0.912 1 增至0.979 9。综合以上分析，经过BSO 算法优化后，BSO-BP 神经网络模型可以准确的表征各道次拉深系数与成形质量之间的非线性关系。

6 MOPSO 算法多目标寻优

本研究中涉及两个冲压成形质量优化目标，即使最大减薄率数值最小以及FLD 成形安全域占比最大。多目标粒子群（MOPSO）算法是在单目标粒子群算法（PSO）上发展起来的一种智能数学寻优算法，适用于多目标优化求解。MOPSO 算法相比于遗传算法而言，其不需要对“变异”和“交叉”进行处理，因此MOPSO 算法编程相对遗传算法较为简易。其次，通过设定初始粒子的惯性权重、全局增量等参数使粒子群在解空间中进行搜索求解最优粒子，全局最优粒子的获得只与设定的收敛精度有关，因此其搜索过程不受其他参数影响，搜索求解过程客观性强，易于获得全局最优解[11-12]。

综上，粒子个数设为20、惯性权重为0.9、全局增量为0.9，收敛精度为1e-7。以吸能盒最大减薄率最小化和FLD 安全域占比最大化为优化目标，基于MOPSO 算法在构建的BSO-BP 神经网络模型内进行最优粒子搜索，得到的最优各道次拉深系数见表6。

表6 优化后各道次拉深系数

7 试验验证

7.1 模拟验证

依据表5 的优选结果，按照前述方法，在Autoform 中完成前5 道次拉深工具体的创建，为规避拉深工艺参数对成形质量的影响，拉深工艺参数的设置同初始分析时完全一致，得到如图10 所示的优化后的OP1～OP5 道次拉深有限元分析结果，OP5 道次拉深厚度云图和FLD 成形极限图如图11所示。

图10 优化后OP1～OP5 道次拉深有限元分析结果

图11 OP5 道次拉深厚度云图及成形极限图

从图10 可以看出，OP1～OP5 道次拉深的FLD 安全域占比均大于10%，最大减薄率均低于30%，满足成形指标要求。从图11 成形极限图可以看出，不存在开裂区，过度减薄区占比由优化前的7.9%降至0%；开裂风险区的占比由优化前的3.17%大幅降至0.49%；安全域占比由优化前的2.03%大幅提升至11.98%。综合以上分析，可看出本文提出的方法优化效果显著。

7.2 实际生产验证

基于上述研究成果指导吸能盒连续模的设计与制造并在笔者公司金丰1000T 多工位全自动冲压生产线上进行实际生产验证，随机抽取20 个吸能盒并利用奥林巴斯超声测厚仪对吸能盒关键部位进行厚度测量，最终测得的吸能盒最薄部位平均壁厚0.8 mm，根据料厚1.1 mm 进行换算，得到最大减薄率为27.2%，与优化后CAE 分析出的吸能盒最大减薄率为28.3%之间相对误差为3.9%。

应用本文提出的方法生产的吸能盒产品质量优良，如图12 所示。