基于DINA模型的民族地区中学生数学学习认知诊断研究
2023-09-12代瑞香尹一行
代瑞香 尹一行
【摘 要】尝试基于认知诊断理论全面、客观测评兵团八年级学生的数学学习水平.研究发现:总体上,兵团八年级学生对勾股定理七大认知属性掌握概率均值达到六成以上;大多数被试关于勾股定理认知属性的掌握模式较为集中;差异性方面,四组被试对属性A4、A5和T7的掌握存在显著差异;普通班学生对于属性A4、A5的掌握明显优于内初班学生.研究结果反映出高阶认知属性的掌握指向核心素养育人现实,要求数学教学置于真实任务、真实情境的背景之下,全面落实单元主题教学,强化学科实践,以促进学生数学核心素养的培养.为此,需要强化教师对课改理念的实践性解读与教学实践的理论性反思,推动教师对认知诊断方法的学习以及对教育教学研究的重视,促进教师跨文化敏感性知识的充实以及文化回应教学能力的培养,最终将核心素养育人落到实处.
【关键词】DINA模型;核心素养;认知诊断;单元教学
0 引言
《义务教育数学课程标准(2022年版)》[1](以下簡称《新课标》)的发布标志着义务教育学段核心素养育人时代的到来,在“三会”的核心素养引领下,小学阶段11个、初中阶段9个核心素养具体表现、大单元教学、真实问题情境创设等新理念的提出为义务教育阶段教育教学育人理念转变、教学模式方法革新以及“教学评一致性”等指明了方向,也给一线教师的核心素养育人实施带来了挑战.在建设教育强国的新时代背景下,以数学为代表的理科教育教学是制约新疆生产建设兵团基础教育高质量发展的关键变量.本研究将基于DINA模型(Deterministic input noisy AND-gate model)对新疆生产建设兵团学生数学认知水平进行诊断,并结合《新课标》深度分析有关问题,以为兵团数学教育发展服务.
1 研究过程
本研究将选择勾股定理这一教学主题,对兵团八年级学生关于勾股定理的掌握情况进行认知诊断,之所以选择勾股定理主题,是因为勾股定理的教与学在沟通数学文化与数学教育现代化方面具有重要价值.
1.1 认知模型的构建
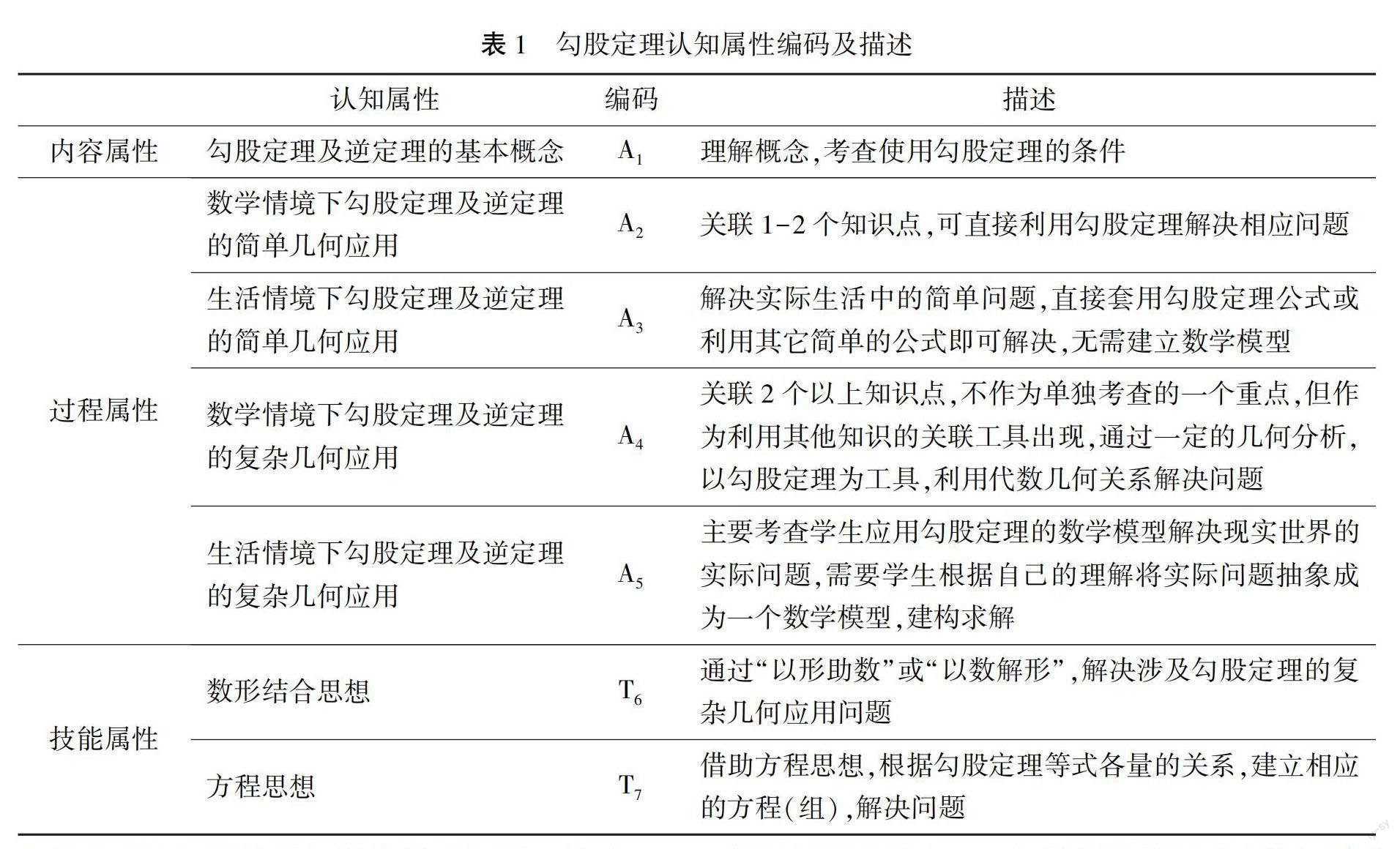
本研究基于《新课标》《初中学业水平考试说明(新疆生产建设兵团2017年版)》,分析人民教育出版社(2013年版)、北京师范大学出版社(2013年版)等十版教材“勾股定理”内容编排结构、例题习题,梳理近十年新疆生产建设兵团中考试题“勾股定理”考点,基于TIMSS测试中的RSM评价三维度(内容维度、过程维度和技能维度)划分标准,初步确定勾股定理认知属性划分为勾股定理及逆定理的基本概念、勾股定理及逆定理的简单几何应用、勾股定理及逆定理的复杂几何应用、数形结合思想及方程思想五大认知属性(几何应用的复杂程度划分借鉴了鲍建生教授“数学习题的难度因素与水平”划分模型中的“知识综合因素”的维度分析).在此基础上发放“勾股定理认知模型专家认证问卷”,综合专家意见,凸显“情境”重要价值,参考路红等(2019)[2]的情境划分维度,修改勾股定理及逆定理的简单几何应用、复杂几何应用等两大认知属性为以下四个认知属性:数学情境下勾股定理及逆定理的简单几何应用、生活情境下勾股定理及逆定理的简单几何应用、数学情境下勾股定理及逆定理的复杂几何应用和生活情境下勾股定理及逆定理的复杂几何应用.结合《新课标》的指导思想,最终确定勾股定理七大认知属性、编码及具体描述如表1所示.同时为进一步确保本研究后续分析的可操作性,选取三道包含预设认知属性的题目,组成口语报告测试卷,择选2名成绩较好和2名成绩处于中等水平的学生,通过口语报告法进行属性层级结构关系验证.结果表明,经专家建议修改后的勾股定理认知模型符合学生的认知结构.
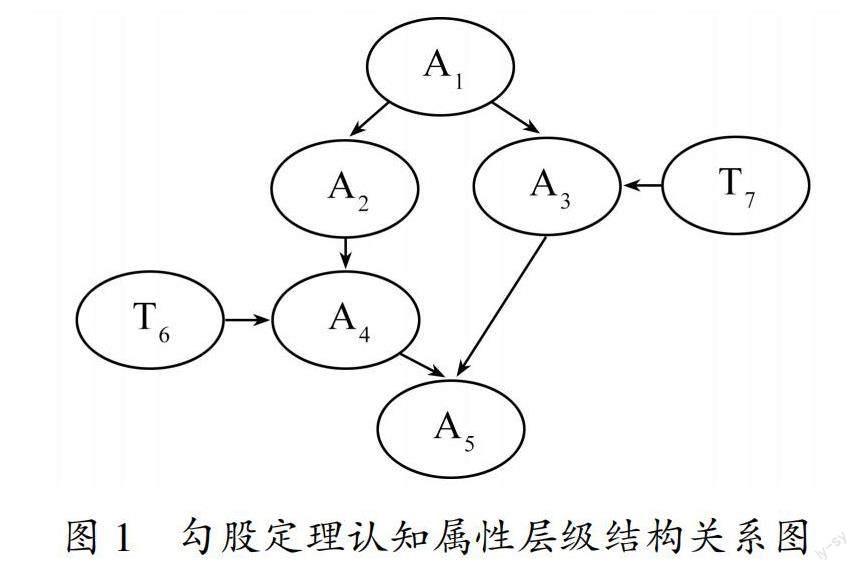
勾股定理认知属性层级结构关系如图1所示.A1属于基础属性;A2,A3属于中层属性;A4,A5属于高层属性;T6,T7作为技能性属性,贯穿以上5个认知属性的掌握,起到桥梁作用.
1.2 认知诊断测试卷的编制
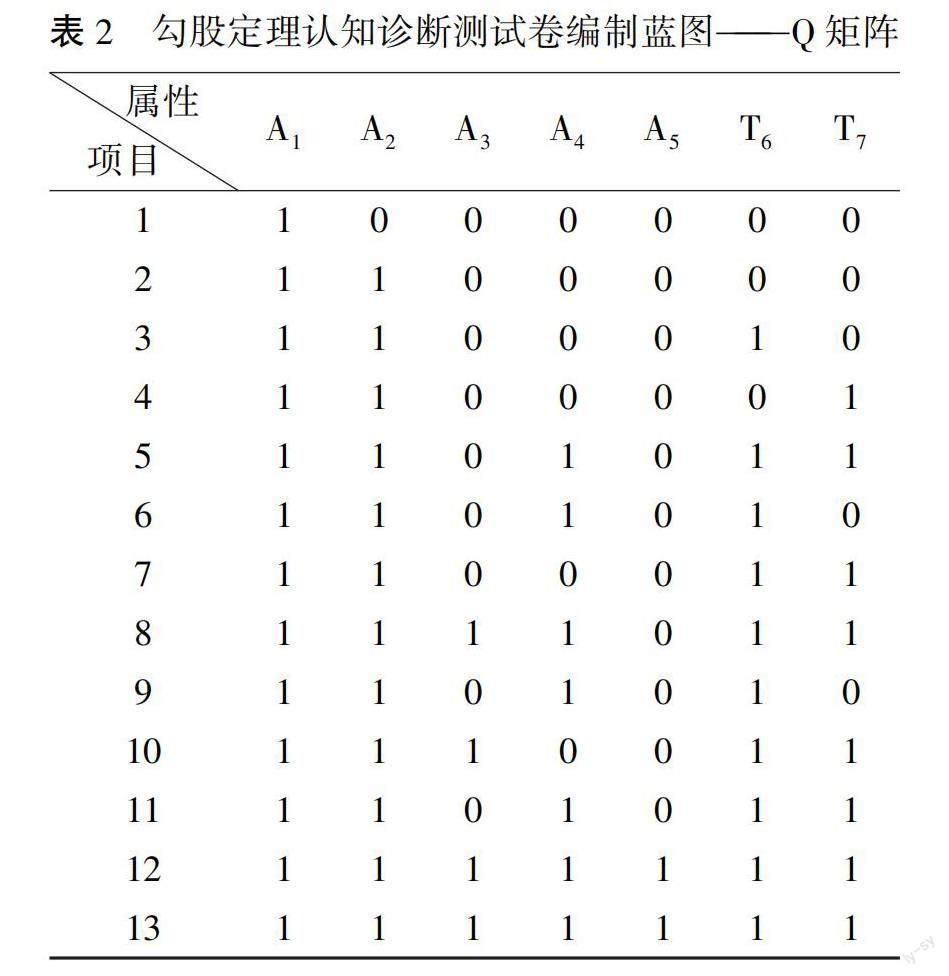
在构建勾股定理认知模型的基础上,根据涂东波(2019)认知诊断测试卷编制原则,得出测试卷的编制蓝图——Q矩阵:由勾股定理认知模型,得到A矩阵,经布尔转换得到R矩阵,再由扩张算法得到27种属性掌握模式,在勾股定理认知属性层级结构关系制约下筛选并删去全0模式后余19种典型项目考核模式.同时考虑到认知诊断实际(不能脱离勾股定理而单独考查属性T6和属性T7),并征询专家意见,删除6种不符合实际考核情况的模式,最终得到一个13行7列的Q矩阵,如表2所示.
据表2,本研究编制勾股定理认知诊断测试卷(预测试),测试卷共计13个项目,由2道选择题、2道填空题及9道解答题构成,并严格按照认知诊断标准进行“0-1”评分,选择题和填空题回答正确编码为“1”,回答错误编码为“0”;解答题的批阅采取等级计分法,若被试在该项目上的实际得分大于或等于项目总分的60%,则编码为“1”,否则编码为“0”.
1.3 实施预测
选取兵团第八师石河子市一所教学环境优良、师资水平较好的初中(该校内初班学生与普通班学生混合编班,每个自然班有内初班学生约15名)八年级2个班共计82名学生进行预测试,无时间限制,剔除无效试卷2份(解答题未写解答步骤),共计回收有效测试卷80份.基于学生答题的统计数据,应用涂东波教授团队开发的认知诊断分析平台(flex CDMs)进行测试卷的相关质量分析.
采用李克特五级量表法编写“勾股定理认知诊断测试卷测试项目所测知识属性认同度调查”问卷,面向28位教龄不同、职称不同的一线数学教师发放.结果表明28位教师对于该测试卷测试项目所测知识属性总体认同度为4.95,并且各个项目均无“不赞同”和“完全不赞同”选项填写者;预测试数据支撑下的属性重测一致性指标均值为0.869,表明该认知诊断测试卷中每一个测试项目的实际考核属性与预设的理想考核属性一致;应用渐进残差均方和平方根(RMSEA)法,计算出RMSEA均值为0.048,小于0.06,表明测试项目与DINA模型拟合良好;测验分类结果信效度方面,用flex CDMs计算出分类一致性指标为0.713,分类准确性指标为0.695,表明预测诊断结果具有较高的稳定性和可靠性.
综上,本研究编制的勾股定理认知诊断测试卷科学有效,可以用于对八年级学生勾股定理七大认知属性掌握情况的诊断测量.
2 正式测试
2.1 数据收集
正式测试仍然选取该校八年级学生(剔除用于前测的两个班),样本人数共计419人,剔除无效试卷9份,回收率为97.85%.为便于后续组别间的差异性统计分析,以任课教师作为分组依据,同一任课教师所任教的两个班级为一组,按照“ID+组别(A,B,C,D)+性别(数字‘1代表男生,‘0代表女生)+班级+序号”的标准进行编码,如IDA00112表示A组01班第12位被试,性别女.
2.2 属性掌握概率分析
应用flex CDMs平台和Excel软件,得到全体被试、各组及不同性别被试在勾股定理七个认知属性的掌握概率,见表3.
据表3,对于全体被试而言,属性A2掌握最好,掌握概率达0.972,其次为T7(0.971),A1(0.955),T6(0.928),A3(0.908),上述5个属性的掌握概率均在0.9以上,较为理想;掌握概率较差的是A4(0.772)和A5(0.619).这说明学生能够掌握勾股定理的一般性应用,但基于现实情境分析、建立数学模型求解勾股定理实际问题的能力仍需进一步提升.
从组别来看,A组被试对属性A2掌握最好,掌握概率为0.935,其次为A1,T6,A3,T7,A4,掌握最差的属性是A5,仅为0.535,低于样本均值;B组被试对属性A1掌握最好,为0.939,同时为四组最高值,其次为属性T6,A2,A3,T7,A4,A5掌握最差,为0.616,比较而言,本组被试对七大认知属性的掌握概率均高于0.6;C组被试对属性T7掌握最好,掌握概率为0.955,同时为组别间最高值,其次是T6,A2,A3,A1和A5,对属性A4的掌握概率仅为0.557,低于0.6,掌握较差.显然,C组被试对于技能维度的属性掌握较好;D组被试对属性A2掌握最好,掌握概率为0.960,为四组最高值,但对属性A5的掌握概率仅为0.581,低于0.6,掌握最差.另一方面,从D组被试对属性A1,A4和A5的表现上来看,D组被试关于A1掌握概率较其他组略低,但对A4,A5的掌握情况却良好,一定程度上反映出,高水平认知属性掌握情况除了受到数学基础这一影响因素之外,还有更多自身和外在影响因素.
进一步对不同组被试关于勾股定理各属性掌握情况作单因素方差分析,结果表明,四组被试对属性A1,A2,A3和属性T6的掌握不存在显著性差异(Sig.=0.063,Sig.=0.548,Sig.=0.162,Sig.=0.840),但对属性A4,A5和T7的掌握存在显著差异(Sig.=0.000,Sig.=0.005,Sig.=0.000).
从性别角度来看,对不同性别被试总体得分、各认知属性掌握情况作独立样本T检验,结果表明,男、女生在勾股定理知识结构总体得分上不存在显著差异性(Sig.=0.802),在各个认知属性的掌握上,男、女生关于属性A4的掌握情况存在显著差异(Sig.=0.003),女生掌握更好,因为A4指向数学情境下的复杂应用水平,故能反映出女生的学习态度以及努力程度优于男生.其余6个认知属性,男、女生对其掌握情況不存在显著差异.尤其是A5,掌握情况均不理想.
同时,考虑到所调研学校的区域特征,我们对此次被试中的“内初班”学生的作答数据进行了统计分析.数据表明,在属性A1,A2,A3和T6,T7掌握上,内初班学生与普通班差别不大(Sig.=0.263,Sig.=0.446,Sig.=0.125,Sig.=0.623,Sig.=0.621),但在属性A4,A5的掌握上,内初班学生明显低于普通班(Sig.=0.002,Sig.=0.000).由此,反映出除了教材、教师等外在因素之外,日常用语、数学语言、情境熟悉程度、师生互动方式、认知特征、教学理念与教学方式等对内初班学生的数学学习有重要影响,教师的跨文化敏感性知识需要补充,教师的文化回应教学能力需要培养.
2.3 屬性掌握模式与归入率分析
属性掌握模式可以直观的反映出学生认知属性的整体掌握情况[3].认知诊断领域常用属性掌握模式归入率作为判断认知诊断测验内部效度的另一指标,掌握模式归入率越高,则表示诊断结果可靠性程度越高[4].本研究应用MAP估计法计算出被试认知属性掌握模式归入率,如表4所示.总体上,全体被试的属性掌握模式归入率均值为90.7%,说明绝大多数被试的属性掌握模式可以归入理想掌握模式.
组别差异上,四组被试理想掌握模式分类和归入率均存在一定的差异.A组被试掌握模式种类多达17种,但属性掌握模式归入率却最低,为88.54%;B组被试掌握模式种类16种,归入率为89.58%;C组被试掌握模式种类13种,归入率为90.63%;D组被试掌握模式种类12种,归入率在四组中最高,为93.44%,说明D组被试对勾股定理的认知与本研究所建立的认知属性模型适配性更高.
进一步分析表明,四组被试关于(1111111)的掌握上,D组最高,为49.18%,说明该组近一半的学生掌握了勾股定理全部认知属性;其次为C组,为38.54%;然后是B组,为34.38%,A组最低,占比31.25%.四个组被试关于(1111011)的掌握上,C组为30.21%,D组次之,为22.13%;然后是B组,为19.79%;A组占比最低,为16.67%.除了(1111111)和(1111011)这两类属性掌握模式之外,四组被试关于其它各种属性掌握模式的人数占比都在5%上下.总体上,D组被试关于勾股定理认知属性的掌握情况最好,C组次之;B组、A组被试的认知水平仅停留在简单应用层面上,掌握情况不理想.此外,基于前文分析,B组被试对七大认知属性的掌握概率更接近于全体被试的平均水平,然而从属性掌握模式分布情况来看,B组的整体掌握情况却不如其他三组,反映出B组被试关于各属性间联结掌握不容乐观,知识链接能力较差.调研中了解到,D组被试所在班级的数学教师教龄长达20余年,B组被试的数学教师为新入职教师,反映出教师专业功底以及持续专业发展对于学生认知水平发展的重要性.
性别差异上,男生属性掌握模式共计17种,归入率为89.6%;女生掌握模式有16种,归入率为91.7%;但在非理想属性掌握模式(如1111110)上,男生占比更高,说明男生思维相对更加发散,不局限于本研究所创建的认知模型,并有意识寻求其它方法建立模型来解决问题.
内初班与普通班差异方面,对于属性掌握模式(1111111),普通班学生归入率为42.65%,内初班学生归入率为19.05%;对于属性掌握模式(1111011),普通班学生归入率为23.92%,内初班学生归入率为12.70%;数据反映出,内初班学生关于整体认知属性的掌握明显差于普通班.其中,对于属性掌握模式(1000000)和(1100000),普通班学生归入率占比共计3.46%,内初班学生归入率占比共计15.88%,说明内初班学生对于勾股定理两大基础属性的整体掌握好于普通班,但在高阶认知属性的掌握上却落后于普通班.统计数据反映了教育的复杂性、数学的抽象性以及指向核心素养的数学教学给教师带来的困难等,数据也再一次表明基础认知属性与高阶属性的掌握之间并非线性关系,学生对高阶认知属性的掌握需要教师在教学以及指导学生自主学习过程中综合考量数学的历史、文化、发展脉络、知识内在关联以及数学的广泛而深刻的应用等方方面面.
从整体来看,普通班学生属性掌握模式共计17种,归入率为90.20%,内初班学生属性掌握模式共计14种,归入率为93.65%,反映出内初班学生的思维方式更靠近本研究所预设的思维结构,也说明其数学思维不够发散,缺乏创新,其数学认知受到语言因素、自身认知特征以及任教教师的数学素养、教学风格等多元因素的综合影响.
2.4 典型个例分析
区别于传统测验,认知诊断可以根据被试的作答反应情况给出被试具体的认知结构,为教师准确把握每一位学生的认知特征以及进行教学补救提供依据.
由表5,筛选出的三位被试掌握模式均为(1111011),未掌握的认知属性均为A5,但总分不同,作答模式也不相同.这三位被试未正确作答的题目多为生活情境下的勾股定理应用问题.反映出A5作为高阶认知属性,具有统摄性,但教学过程中教师过于关注知识点的传授,缺失整体化、系统化教学,导致该认知属性掌握较差;也反映出传统教育教学理念对于数学与生活联系的忽视,教学或作业设计中没有注重创设与学生生活现实紧密联系的真实问题情境,更不会有跨学科情境的创设.
由表6,两位被试的总分均为10分,但其掌握模式却不同:被试IDC10517未掌握属性A5,被试IDC10634未掌握属性A4和A5,其它基础认知属性均掌握较好.这反映出,基础认知属性的掌握情况并不能直接正迁移到高阶属性的掌握.数学基础打得牢并不一定能灵活应用数学知识解决复杂现实问题,反映出高阶属性的掌握受诸多因素影响.对于被试IDC10517,虽然掌握了A4,但属性A5并未掌握,说明解决纯粹数学应用问题与解决复杂生活情境问题之间并不能直接画等号,数学的现实应用更加复杂和多变.
此外,被试IDC10517关于项目2和项目3均作答错误(1001111111101),但经认知诊断,却不能判定该被试未掌握属性A2或A3.复盘该被试的测试卷发现,这两个项目的错误原因是粗心大意,反映出认知诊断评价的严谨性.同时就该被试的属性掌握模式(1111011)来说,其并未掌握认知属性A5,按说无法解答项目13(该项目需要建立模型进行解决),但是被试却正确解答了该项目.分析发现该被试对属性A4掌握较好,在作答过程中灵活应用了一次函数相关知识.分析揭示出该被试不仅数学基础良好,而且对数学知识的整体理解水平较高,思维敏捷.这一个案分析结果表明传统知识取向教学向核心素养教学转型的必要性和紧迫性.
3 結束语
研究发现,当前兵团基础教育阶段的数学教育教学尚未向素养取向进行转型与实践.为推动兵团基础教育高质量发展,需要关注几个方面的问题.
第一,基于认知诊断,能实现对学生学习成效的全面、客观诊断,为补救教学提供重要参考,也有助于发挥学生的主观能动性.教师在进行特定主题教学时,可以根据研究所建立的认知模型,遵照知识本身的结构有逻辑的开展教学.基于特定知识点或者单元教学主题构建认知模型,可以帮助教师深层次了解学科知识结构与本质,可以多角度诊断学生的真实学习情况,在认知诊断报告结果的支撑下,教师可以通过分析了解学生普遍存在的问题(共性困难点)、学生个体所存在的问题(个性困难点),有针对性的开展补救教学,课后也可以根据该结果筛选学习资源,助力作业分层,以提升学生高阶认知属性掌握水平.
此外,认知诊断结果能为教师分层教学提供重要参考,以实现因材施教之目的.考虑到隶属同一属性掌握模式的学生,其知识结构和能力类似,因此可以根据学生的属性掌握模式,制定针对性的学习路线图,使得分层教学效果达到最优.以本研究中的属性掌握模式为(1100011)的学生为例,可以为其构建(1100011)→(1110011)→(1111011)→(1111111)的学习路径,即先对其进行生活情境下勾股定理简单几何应用相关题目的练习,使其掌握模式变为(1110011),随后在掌握属性A2的基础上,拓展提升知识难度,促成属性A4的掌握.
第二,认知诊断能起到从传统知识传授到素养培养教育的桥梁作用.本研究表明,大部分学生的掌握模式集中在(1111111),(1111011)两种类型上,需要进一步提升属性A5的掌握水平.A5指向复杂现实应用,这与《新课标》的“学业质量标准”考核要求完全一致.A5作为高阶认知属性,掌握难度较大.学生的问题在于,对情境的理解,对从数量与数量关系、图形与图形关系和事物的具体背景中抽象出数学概念以及概念之间的关系、一般规律和结构,并用数学语言予以表征等方面的表现较差.
实际上,无论何种数学知识,其高阶认知属性都与复杂实际应用密不可分.因此,教师要将学习置于真实任务、真实情境的背景之下,注重发挥情境设计与问题提出对学生主动参与教学活动的促进作用,通过问题驱动,让学生充分实施学科实践,感受数学在现实世界的广泛应用,体会数学的价值.
第三,所有认知属性,尤其是高阶认知属性的掌握需要单元教学的全面实施.本研究表明,基于特定教学主题的一切认知属性从低到高划分为知识、技能和素养等三个层次.基于特定教学主题的各认知属性既有层次又有密切联系.认知诊断属性划分体现了基础性、层级性,基础认知属性是发展高阶认知属性的基础,但不是必然的因果关系,高阶认知属性的掌握需要以知识的融会贯通以及基于真实情境问题的灵活、复杂实践为前提.所有认知属性,尤其是涉及复杂数学应用和复杂生活应用的高阶认知属性的掌握,需要数学教学以教材为基础,从培养学生核心素养角度出发,对教材内容进行优化重组,实施指向核心素养培养的单元教学,以突出数学内容的主线以及知识间的关联性,强化学科实践,将知识、能力、体验、思维、情感、思想方法等有机融合在一起,促进学生对高阶认知属性的掌握.
再者,基于单元教学的认知诊断会比单一知识点的诊断效果要好:单元整合的内容,因其系统性和整合性,更有利于划分难易区分的认知属性,也能更好地从核心素养育人的要求方面进行客观诊断以及补救教学.
总之,核心素养的教育时代已经到来.教师作为教育发展的奠基者,课改的执行者和实践者,首要任务是改变和提升自己[5].基于当前兵团基础教育师资年龄结构不合理,水平差距大的现实,有必要在教师培训和教师自主发展上蓄力,使其充分立足《新课标》的指导思想和实施建议,加强对课改理念的实践性解读与教学实践的理论性反思,把握教学内容主线与相应核心素养发展之间的关联,培养其“教养融通”的专业育人技能,在做中学、学中思、思中做,既成改革之事,又成改革之人[5],“不打折扣”地全面落实立德树人根本任务,将核心素养育人落到实处.
参考文献
[1]中国人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[2]路红,杜宵丰,綦春霞.初中生数学运算素养的实证研究及思考——基于华北中部地区某市的数学学业监测[J].教育测量与评价,2019(12):34-42.
[3]涂东波,戴海琦,蔡艳,等.小学儿童数学问题解决认知诊断[J].心理科学,2010,33(05):1461-1466.
[4]涂东波.高级认知诊断[M].北京:北京师范大学出版社,2019.
[5]张民生.在课程改革中培养面向未来的高素质教师队伍[J].上海教育科研,2022(06):1.
作者简介 代瑞香(1980—),女,山东曹县人,副教授;主要从事数学教育研究.
尹一行(1998—),女,山东潍坊人,硕士,助教;主要从事数学教育研究.
