激活“爱问”天性，助力数学“乐学”

吴贤

摘要：让儿童提出自己的数学问题，依据儿童的问题推进数学教学。《认识图形（一）》一课教学，通过“课前问题秀”，让儿童用数学的眼光观察现实世界，发现并提出具有儿童视角的数学问题；通过“前置任务单”，让儿童在具体的任务情境中动手操作、观察比较，提出自己注意到的数学问题，并借助“课中问题场”，让儿童选择可研究、有价值的问题，游戏化、综合化地持续开展指向学习目标的数学学习；通过“课尾问题链”，让儿童在学习后回顾反思，生发新的数学问题，形成可延展的问题意识。

关键词：小学数学；问题提出；幼小衔接；《认识图形》

2021年3月，《教育部关于大力推进幼儿园与小学科学衔接的指导意见》发布。其附件2《小学入学适应教育指导要点》围绕儿童进入小学所需要的关键素质，提出了四个方面适应的要求。其中，“学习适应”的首要发展目标为“乐学爱问”。2022年3月，《义务教育数学课程标准（2022年版）》发布，“问题提出”成为体现和落实数学核心素养的重要教学目标和手段［1］。

“乐学爱问”需要儿童在观察、阅读、讨论等情境中，发现问题、提出问题，对不懂的现象进行追问和探究；“问题提出”更是要让儿童从单一、被动的问题解决者转变为主动的问题提出者与问题解决者，进而主动参与数学探究活动，发展创新意识。无论“乐学爱问”还是“问题提出”，都表明要让儿童提出自己的数学问题，依据儿童的问题推进数学教学。这对一线数学教师，尤其是低年段数学教师，无疑是一个巨大的挑战。

近年来，笔者所在的小学数学团队一直致力于“转学成教”教学方式的研究，其中的一个重要子课题是培养儿童的提问力。借助前期在中高年级研究的经验，团队在低年级积极营造敢想敢问的提问氛围，在数学教学的不同环节让儿童提出问题，激发儿童的求知欲，提升儿童的学习兴趣，让儿童顺利达成学习适应的目标。具体来说，通过“课前问题秀”，让儿童用數学的眼光观察现实世界，发现并提出具有儿童视角的数学问题（可以在亲子互动中生活化地解决问题）；通过“前置任务单”，让儿童在具体的任务情境中动手操作、观察比较，提出自己注意到的数学问题，并借助“课中问题场”，让儿童选择可研究、有价值的问题，游戏化、综合化地持续开展指向学习目标的数学学习；通过“课尾问题链”，让儿童在学习后回顾反思，生发新的数学问题，形成可延展的问题意识。

苏教版小学数学一年级上册《认识图形（一）》一课教学，正是基于这样的思考，在幼儿园认识图形的基础上，通过儿童自己的问题，引发认知冲突，在游戏活动中，初步体会问题解决的过程，达成学习目标的一次探索。

一、教学实践

（一）“课前问题秀”：在实际生活中发现数学问题

师掌声有请今天的“提问小达人”。

生同学们好！我今天的问题来自牛奶盒。（出示图1）我妈妈特别关心我的健康，经常给我买牛奶。这个星期天，妈妈又给我买了一箱牛奶。我拿牛奶的时候发现：怎么这些牛奶盒都被做成长方体呢？为什么不是圆柱形或者球形呢？我和妈妈一起想。妈妈说，可以找一下圆柱形或者球形的东西来看一看。（出示图2）我找到了胶棒，它是圆柱形的。我发现，几个胶棒拼在一起，中间会有很多缝隙，要是牛奶盒也做成这样，装的牛奶不就少了吗？我还找到了一个小皮球，一碰，它就会滚，要是牛奶装在里面，不是很容易洒出来？而且，球和球放在一起，之间的缝隙更大了。看来，牛奶盒做成长方体，放得多还不容易洒。这就是我今天的提问和我的解答。谢谢大家！你们还有什么问题呢？

生牛奶盒能做成正方体吗？

生装牛奶的箱子为什么也是长方体的呢？

师谢谢今天的“提问小达人”，也感谢两位同学的提问。瞧，喝牛奶时，也能发现数学问题。借助身边的物品，和爸爸妈妈一起看一看、想一想，对问题还能有自己的想法，真了不起！新提出的问题，也非常有意思。今天，我们就一起认识这些有趣的图形，在学习中进一步思考我们提出的问题。

提问，是儿童的天性。引导儿童用数学的眼光观察现实世界，是儿童发现和提出数学问题的基础。“课前问题秀”，为儿童发现和提出实际生活中的数学问题，提供了动力和平台。儿童以“提问小达人”的身份，在课前的2—3分钟内，交流自己发现的与课题有一定关系的问题，并给出一定的思考和解答，不断积累数学观察的经验，产生积极的数学思考，也让同伴在日积月累中丰富了对数学的感知，获得了一定的提问经验。

（二）“课中问题场”：在任务情境中聚焦数学问题

1.“问题真奇妙”：交流问题，指向学习目标

师留心生活，我们能发现牛奶箱中的数学问题。（出示前置任务单，内容如下）课前的学习任务中，同学们也提出了很多有意思的问题。

【我来研究】

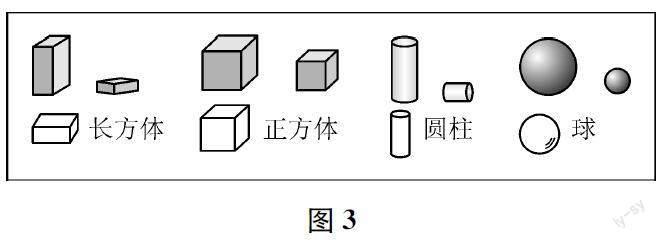
1.幼儿园里，我们一起玩过积木。积木里，有长方体、正方体、圆柱，还有球（如图3）。

（1）找一找自己小时候的积木，找出这几个图形，把它们的名称说给爸爸妈妈听。

（2）动手摸一摸，滚一滚，搭一搭，你有什么感受？你发现了什么？和爸爸妈妈交流。

2. 在家里找一些长方体、正方体、圆柱、球形的物品，动手摸一摸、滚一滚。

【我的问题】

研究中，你还有什么问题呢？画一画，写一写，把你的问题记录下来。

师让我们一起进入今天的“问题真奇妙”。先请同学们在小组里有顺序地和同伴分享自己的问题。

（学生在小组内依次借助学习单，介绍自己的问题。）

师让我们一起来听听几位同学的问题。

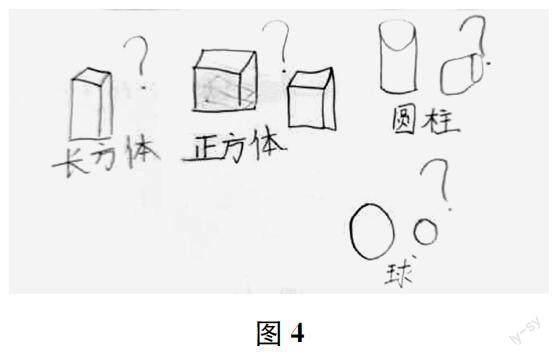
生（出示图4）我的问题是：为什么长方体叫作长方体，正方体叫作正方体，圆柱叫作圆柱，球叫作球呢？

（学生全都笑了起来。）

师虽然这个问题像绕口令一样，但是真的发人深省啊！是啊，为什么这些图形要叫这个名字呢？和这些图形的形状有什么关系呢？

生（出示图5）我的问题是：为什么长方体、正方体不会滚，而球能滚？

生（出示图6）我想问大家：为什么球可以到处滚，而圆柱只能朝着一个方向滚？

生（出示下页图7）我在搭一搭的时候发现，长方体、正方体都很好搭，而球特别不好搭，圆柱倒下来也不好搭。这是为什么？

生我的问题是：为什么我们打的是乒乓球，而不是“乒乓方”呢？

师几位同学提出的问题，让我们对今天要认识的图形有了新的研究方向。

借助课前任务中的活动经验，提出指向学习目标的数学问题，对一年级学生来说，是不小的挑战。儿童的提问，需要由实际情境中的认知冲突产生线索，还需要用数学的语言进行表达。鉴于一年级学生的特点，教师需要提供操作性、活动化的任务情境，让儿童图文并茂地表征，口语化地表达。这些充满儿童趣味的表征和表达，以及教师对儿童问题的梳理和筛选，会让儿童保持对问题的敏感和好奇，并进一步在相互交流中积累提问的一般方法和策略，也让儿童的学习需求与课堂的学习目标有了很好的一致性与协调性。

2.“游戏挑战赛”：探索问题，实现学习目标

（1）“手感大比拼”游戏

师还记得第一个问题吗？（再次展示图4）不着急回答。我们先来玩一个“手感大比拼”的游戏，一边玩，一边思考这个问题。首先了解一下游戏规则。（同步展示布袋子和其中的积木）老师给每个小组准备了一个这样的布袋子，里面装着6块积木。一起来说说它们分别是什么图形吧。

（学生根据出示的积木说出图形的名称。）

师现在，把这些积木装回袋子里，再把手伸进袋子里，摸一个积木——注意，不能看，只能摸——能说出图形的名称，就算胜利。考验手感的时候到了，谁愿意先来试一试？

生（按照规则摸到一个积木而不拿出布袋）我觉得是一个长方体。

师拿出来举高点，给大家看一看。

（学生拿出积木。全班惊叹、鼓掌。）

师你的手感真棒！给你点赞。同学们，想试试吗？待会儿，同桌两人一组，确定好谁先摸、谁后摸，然后一人摸图形说名称，另一人做“小老师”：说对了，就给他点个赞；说错了，则轻轻刮一下他的鼻子。每人轮流摸三次，看看谁能获得全部的三个赞。好，游戏开始。

（学生分组讨论游戏顺序，有序完成游戏活动。）

师获得了全部三个赞的，手举高！

（学生举手。）

师哇，你们的手感真棒啊！给他们掌声。

（学生鼓掌。）

师老师也想问一下：有谁被轻轻刮了鼻子吗？

（学生举手。）

师摸哪个图形的时候手感出错了？

生（拿出正方体）我说错了，说成长方体了。

师一起来想象一下，这个图形摸起来和长方体有什么不同呢？

生正方體方方的，每个面摸起来都一样大。

生长方体要么长长的，要么扁扁的，很好认。

生长方体，长方体，长长的呀！正方体才是正正的、怎么转都一样的手感。

师课前，我们观察过每个图形；刚才，又通过“手感大比拼”游戏摸了图形。现在，再来想一想第一个问题：为什么长方体叫作长方体，正方体叫作正方体？大家有感觉了吗？

（全班点头回应。）

师那么，为什么圆柱叫作圆柱，球叫作球呢？可以用老师这里的大积木，边说边展示给大家看喔！

生（边说边展示）你们看，圆柱上面和下面都是圆形，但是它站起来又像个柱子一样。它既有圆形又像柱子，当然要叫圆柱啦！

生我们体育课上踢的足球、小时候拍过的小皮球都是球，和这个球是一样的，所以我觉得，所有这样的形状都叫作球。

生球都是圆乎乎、可以滚来滚去的，就和我们平时踢的球一样。

师看来，每个图形的名字，都和它的形状、它与其他图形不一样的特点有关系。让我们再次念一念这些图形的名字，要念出你对它们的感觉喔！

（学生根据出现的积木念出图形的名称。）

（2）“我说你来猜”游戏

师通过“手感大比拼”游戏，我们对第一个问题有了自己的思考，真棒！老师还想和大家玩一个“我说你来猜”的游戏，看看大家对这些图形的特点是不是更有感觉了。“我说你来猜”，其实就是老师在袋子里摸一个图形，说一说这个图形的特点，看看谁能够在头脑里想象出这是什么图形，再把它的名字说出来。准备好了吗？闭上眼睛仔细听，在头脑中想象它的样子。

师（摸一个长方体在手上）这个图形的每一个面都是平平的。

（立刻有学生举手。）

生这是长方体。

生不对，是正方体。

生我觉得，可能是长方体，也可能是正方体。

师老师再摸一摸。啊，这个图形还是长长的。

生（齐）是长方体。

师真的吗？让我们一起看一看。（拿出积木，确认是长方体）为什么仅凭两句话，你们就能确认是长方体，不再认为是正方体了？

生（用两个积木对比）长方体放在桌子上，翻一下，有时候是高高的，有时候又是矮矮的。而正方体怎么翻都是一样高的，就是刚刚说的，正正的，感觉没什么变化。

生长方体有的高、有的矮，但正方体摸起来就是一样的，每个面都一样。

师那为什么没有人猜是圆柱，也没有人猜是球呢？

生因为圆柱有平平的面，也有弯弯的面。

生球没有平平的面，它是圆圆的，只有弯弯的面。

师说得很有道理！再摸一个。（摸一个圆柱在手上）哇，这次的图形是会滚喔。

生老师，它是能到处滚，还是只能朝一个方向滚呢？

师你们希望老师回答这个问题吗？为什么？

生要的要的，这样我们就知道到底是圆柱还是球了。

师那老师告诉大家：这个图形有时候会滚，有时候又能站得很稳。

生（齐）圆柱。

生肯定是圆柱。你们看，当我把圆的这个面放在下面，它就能站稳了。但是，倒下来后，它又能滚了。

生球轻轻一碰，就会到处滚，就像调皮的小朋友，根本停不下来。

生搭积木的时候，圆柱可以搭，球就很难搭。

师（再次出示图5、图6、图7）那这三个问题，现在你有想法了吗？

生我觉得是因为长方体、正方体的面都是平平的，没有弯弯的；平平的面放在桌子上，就能和桌子贴在一起。

生我补充，圆柱有两个面是平平的，所以，我们搭积木的时候，如果将这两个面（之一）放在桌子上，也能放得很穩。

生球就不行了，它的面弯弯的、圆圆的，没有平平的地方，所以会四面八方地滚。

生圆柱也有弯弯的面，不过只有一圈。如果倒下来，这个弯弯的面就能滚了。

师同学们的发现，让这三个问题有了一些答案。是的，平平的面，我们称之为平面；弯弯的面，我们称之为曲面。平面摸起来平平的，能让物体站得很稳；曲面弯弯的，能让物体滚动起来。平面和曲面，构成了我们今天认识的不同的图形。

（3）“超级连连看”游戏

师不同的图形，在生活中也有不同的用处。（出示图8）老师带来了这样一些生活中物体的图片，一起来认一认。

师接下来，我们要根据这些图片，玩“超级连连看”游戏。规则很简单，老师出示图片，你们在小组里说出这个图片上物体的形状名称，再找到对应的图形积木，把它举起来。

（教师出示图片，学生小组合作找出积木。）

师老师发现，出现冰箱这个图片的时候，大部分小组举起的是长长的积木，有一个小组举起的是扁扁的积木。你觉得谁找得对呢？

生我觉得，要举起长长的积木，这个形状和冰箱特别像。

生我们小组觉得，冰箱是长方体，所以长方体的积木都可以。

师的确，长长的这块是长方体，扁扁的这块也是长方体，冰箱的形状是长方体，两种积木都是正确的。（稍停）足球、篮球、排球都是球，还有乒乓球。还记得最后一个问题吗？为什么我们要把它们做成球的形状，而不是方的呢？找出正方体和球，摸一摸、想一想、说一说。

生如果我们打的是“乒乓方”，那么它有的时候平平地落在桌子上，有的时候是尖尖的那个角落在桌子上，会很不好打。

生球不管怎么打，落在桌子上的部分都是一个很小的点，这样更容易弹起来。

生球很均匀，怎么转动都是一样的，从哪个方向看都是一个圆。正方体要是侧过来看，就不那么一样了。

师对这个问题，同学们的思考都非常精彩。当然，我们在今后的学习中，还会学到相关的数学知识。相信大家不断积累，会有更多的发现和认识。

（4）“积木搭高高”游戏

师好了，探索了这么多有意思的问题，最后我们来玩“积木搭高高”游戏，看看对于这些图形，我们还能有什么新的体会。对这个布袋里的6块积木，待会儿大家在小组里讨论，精心挑选4块来，看看哪一组挑选出的积木能搭得最高。友情提醒：不仅要搭高高，还要说说为什么你们要选择这4块积木，怎样才能搭得最高喔！

（学生分组活动。）

师（出示图9）老师发现，大部分小组都选择这4块积木搭成了这样，但有一个小组和大家不一样。比一比，哪一种搭得更高？

生第一种搭得高。（同步指图）这块长方体积木像这样竖着放，比这样放要高。

师这样选、这样搭一定最高吗？

生我们比较了所有的6块积木。球不行，其他图形都没法放到它上面，它放到最上面也会掉下来。正方体比这个扁扁的圆柱立起来还要高一些，另一个圆柱和这个长方体立起来是最高的，所以我们选了这4块积木这样搭。

师（对搭法不一样的小组）听了他们组的介绍，你们组有什么想说的？

生我们刚刚也发现了，如果把这个长方体转个方向再放，就更高了。

师看来，形状相同的积木，高度也不一定相同；就是同一个积木，放置的方法不同也可能让它的高度发生变化。（稍停）今天，我们借助同学们自己提出的问题，对长方体、正方体、圆柱和球有了新的认识。自己提出问题，在学习中思考和解决这些问题，同学们真棒！让我们把掌声送给带来这几个问题的“小作者”们！

基于对儿童问题的预设，教师可以借助模块化的小游戏或主题性的大任务，帮助儿童进一步积累数学认识、提升数学理解，并和儿童一起寻找解决问题的路径和策略。这里的四个小游戏，虽然是教师预设的，但是与学生可能关注的问题以及本节课的学习目标有着内在的一致性。教师可以利用这些游戏，以学生提出问题的解决（或初步解决）为指向，引发学生探索发现，从而实现本节课的学习目标。

（三）“课尾问题链”：在持续思考中延展数学问题

师同学们，在数学学习中，学会提出问题，可以让我们更会观察和发现，也更会思考和表达。解决了这样几个问题，你还能提出新的问题吗？

（学生静静地思考。）

生蛋糕为什么要做成圆柱形呢？

生水杯为什么要做成圆柱形呢？倒下来不是很容易滚到地上吗？

生为什么生活中到处是长方体，正方体却不是很多呢？

生为什么我们的头是球一样的形状，而不是长方体，也不是正方体呢？

……

师这些问题中，有些，大家可以课后和小伙伴或爸爸妈妈一起讨论研究；有些，期待大家在后续的数学学习中进一步思考和探索。今天这节课就上到这里。

通过回顾反思，学生意识到问题对于学习的重要价值，体会到本节课共同研究的问题与学习目标之间的联系，从而保持持续提问的意识。通过新的问题，让学生始终处于“问题提出—问题解决—新问题提出—新问题解决”的“链式反应”中。

二、教学思考

回顾整节课的教学过程，可以发现，依据儿童自己的问题开展教学，能更好地激活儿童的思维，引发儿童的思考，激发儿童对数学学习的兴趣。

首先，日积月累下的“课前问题秀”，让儿童对提出数学问题不再有畏惧的情绪，更让儿童体会到观察和发现的乐趣。每节课始的两三分钟，“提问小达人”会带來怎样的数学问题？这个（些）问题会唤醒儿童怎样的生活经验？会给予儿童怎样的数学思考？这些如同一个个盲盒，会让每节数学课充满期待和未知的快乐。从鞋子里的数字密码到饮料瓶上“0”的秘密、门牌中数的含义，再到脑袋的形状、牛奶盒的形状……儿童开始关注自己所处的世界，关注身边的数学信息，并进行初步的数学思考，从不自觉的日常提问走向自觉的数学提问。虽然这些问题的表述还不够精准，解决也未必正确，甚至所需要的数学知识与技能还没有学过，但这并不妨碍儿童在这一过程中形成对数学问题的敏锐直觉、对未知数学奥秘的好奇与探索。而正是这样聚沙成塔式的过程，让儿童的好奇心一直持续，使儿童的探究精神逐步建立。

其次，任务情境下的“课中问题场”，让儿童获得了自主提问的动力，也为儿童观摩学习不同的问题解决创设了良好的平台。借助学习任务，儿童自主进行一定的动手操作、实践探索，从中产生认知冲突，从而提出与学习目标高度相关的数学问题。在组内交流、全班分享中，儿童感受自己和他人问题的不同含义，再次激活自主学习的经验，并产生解决问题的需要。课上，教师全班展示的问题，无论“为什么长方体叫作长方体，正方体叫作正方体，圆柱叫作圆柱，球叫作球呢？”，还是“为什么长方体、正方体不会滚，而球能滚？”“为什么球可以到处滚，而圆柱只能朝着一个方向滚？”等，都是儿童在摸一摸、滚一滚、搭一搭的操作过程中真实体会到的现象、主动观察到的场景、生动自然地提出的问题，更贴合儿童的认知水平，也更符合儿童的理解需要。在教师加工后，这些问题真正指向儿童学习的关键节点，能更好地触发儿童的数学思考和表达。

最后，回顾反思中的“课尾问题链”，让儿童对数学问题提出形成了学习的开放式链接。过去，数学学习囿于分析和解决问题的局限性思维：数学问题必须有解，数学学习就是解决问题。而指向核心素养的问题提出，则不仅是一种学习方式、教学手段，更是儿童需要经历的认知过程，需要达成的学习目标，需要培养的关键能力。因此，最后这个环节提出的问题虽然不能当堂解决，甚至在未来较长的时间内也无法解决，但是提出问题本身就是学习，就是儿童主动参与和创新精神的体现。一年级儿童在学习后进一步提出问题，是有不小难度的，更需要教师保护其可贵的问题意识，理解其合情理的“傻问题”“怪问题”“无厘头问题”，赏识其有价值的问题，并在可能的情况下，把儿童的问题引入后续的学习中，让“提问—学习—提问”真正形成有意义的循环。

参考文献：

［1］ 蔡金法，王涛.体现和落实核心素养：解读新课标中的“问题提出”［J］.教育研究与评论，2022（10）：41-2.