基于CNN 的卫星内部结构频域响应间接测量方法

彭瑾坤，武文华,2*，顾乃建，胡 奇

（1.大连理工大学 工业装备结构分析优化与CAE 软件全国重点实验室，大连 116024；2.大连理工大学宁波研究院，宁波 315000；3.北京卫星环境工程研究所，北京 100029）

0 引言

抢占低轨通信资源，构建大规模卫星星座，对发展下一代通信技术和维护国家安全具有重要战略意义。国外先后出台并实施了“铱星”、OneWeb、GlobalStar 等星座计划；近年来，SpaceX 的“星链”计划也发展得如火如荼，将构建由4.2 万颗小卫星组成的互联网星座系统。我国的互联网星座必须加快发展、迎头追赶，这就要求大幅提升卫星的生产制作效率，由此引入了卫星生产线的概念。而力学试验作为卫星研制过程中的必做项目，须通过技术创新和模式转型实现快速试验，才能满足卫星脉动式快速生产的要求。

力学试验的主要目的是通过地面环境模拟考核航天器承受运载火箭发射段动力学环境的能力，通过对星箭对接面处振动的等效，经过结构的传递，最终获取航天器舱体内外部关键部位的动力学响应，以验证设计、工艺是否满足发射要求[1]。生产线卫星力学振动试验存在着同一生产线卫星数量多、结构内部响应测量困难以及内部测点传感器拆装困难等问题，成为卫星脉动式快速生产的瓶颈。如果能够利用外部测点响应间接测量出准确的内部测点动态响应，则可以达到节省试验成本、提高测试效率以及加快卫星生产节奏的目的。

现有的间接测量方法大都依赖于理论模型与有限元模型[2-5]。然而，卫星结构内外测点的动力学响应间存在着强非线性关系，难以利用传统的力学模型间接测量方法获得准确的间接测量结果。而深度学习方法拥有强非线性映射能力以及强数据表征能力，可以绕开数据—经验—数据的传统研究路径，通过数据驱动模型直接构建不同数据之间的映射关系[6]，因此已广泛应用于诸多领域的间接测量[7-8]，但在卫星领域的研究和应用仍较少。

本文主要开展生产线卫星产品的内部结构响应间接测量技术研究。基于真实卫星结构力学试验获得的卫星表面的加速度数据，对卫星内部结构响应进行间接测量，建立基于深度学习的内外测点间加速度响应的映射关系，探索间接测量获得内部结构高精度响应方法的可行性。

1 卫星内部结构响应间接测量模型

1.1 内外部响应间的关系

随着卫星结构的复杂化和复合材料（如蜂窝板、碳纤维等）的广泛应用，结构动力学响应呈现出强非线性，导致动力学响应的测量过程中结构内部与外部的频域响应之间存在强非线性关系[9]。但从理论上仍可认为存在一个可以描述结构内部与外部测点响应之间映射关系的方程

式中：xi为结构外部可测点动态响应；yj为结构内部关注点动态响应；Φi,j描述f频率下，结构i点响应与j点响应之间的映射关系；N为结构自由度。理论上，如果构造出函数Φi,j的近似非线性关系模型

就可以通过输入可测点动态响应xi(f)求解关注点的动态响应yj(f)。模型的输入通常选择工程实际中易于直接测量的物理量，如加速度、应变等数据。式(2)中：y～i(f)为 基于模型 Φ～i,j计算出的内部测点响应数值；ε为允许误差上限。

综上所述，内部测点响应间接测量问题的实质就是求解外部测点和内部测点响应之间的映射关系函数Φi,j，而从物理机理直接推导出其近似非线性关系模型 Φ～i,j是非常困难的。常规的线性回归、多项式回归和岭回归等传统方法以及多层感知机、极限学习机和高斯过程回归等机器学习回归方法都难以拟合复杂非线性关系，无法直接用于内部测点频域响应的间接测量。

1.2 卷积神经网络

卷积神经网络（CNN）是一种前馈神经网络，近年来在图像识别和目标检测方面有着出色的表现。CNN 的基本结构主要由卷积层（convolutional layer）、池化层（pooling）和全连接层（fully connected layers）组成[10]，如图1 所示。

图1 卷积神经网络结构Fig.1 Structure of CNN

卷积层使用设置的卷积核对输入特征按照步长依次进行局部卷积运算，具体的卷积运算式为

池化层通常接在卷积层后面，对特征图进行降维，同时保留重要特征。池化方法主要为最大值池化（max pooling）和平均值池化（mean pooling）。池化层一般只进行降维操作，不需要进行权值更新。本文采用最大值池化操作，其具体的运算过程表达式为

全连接层的作用是将交替的卷积层和池化层所提取到的特征进行整合并再次提取。全连接层的输入是将最后一个卷积层或者池化层的输出特征图展平为一维特征向量，再经加权求和并通过激活函数得到的，全连接层的运算过程表达式为

式中：yl为l层的输出；ωl为权重矩阵；xl-1为第i层的输出值；bl为偏置项。

1.3 间接测量深度学习模型

尽管许多研究成果已表明基于CNN 训练的回归模型可以深度挖掘数据中的隐藏特征，并在图像识别和目标检测方面有着出色的表现[12-15]，但其对于数据预测与映射关系构建方面的能力仍有待验证；不过，CNN 在训练过程中也是将图像或视频处理成矩阵的形式，因此将图像或视频作为CNN 的输入与将外部测点响应数据作为输入并无本质区别，考虑到由于池化层与卷积层的存在，CNN 有着相较于其他神经网络更强的特征提取能力，本文利用CNN 构建卫星结构内部测点频域响应深度学习间接测量算法，其具体步骤如图2 所示。

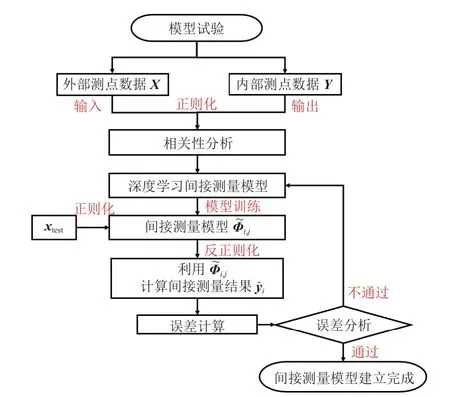
图2 基于深度学习的内部测点响应间接测量算法框架Fig.2 A deep-learning based algorithmic framework for indirect measuring of internal measurement point response

步骤1：通过动力学试验获得卫星结构的频域响应数据[X,Y]，X∈Rk×n为外部测点的响应（输入），Y∈Rk×n为内部测点的响应（输出），其中n表示训练样本长度，k为可测点的数量；并将数据划分为训练集[xtrain,ytrain]与测试集[xtest,ytest]。

步骤2：对获得的响应数据进行相关性分析，选取与每个内部测点相关性较大的m个外部测点的响应数据进行输入与输出的划分[in×(m×l),on×l]，l为内部测点数量（本文中m=10）。

步骤3：基于CNN 构建用于训练频域响应间接测量模型的神经网络模型结构。

式中：{Hx(ωi)}、{Ha(ωi)}分别为激励频率ωi处的直接测量和间接测量的频率向量。与MAC 值相似，χs(ωi)也在0～1 之间变动，当其值为1 时表示完全相关；但是该系数对于频响函数成比例的情况不敏感，即只要{Ha(ωi)}=κ{Hx(ωi)}（κ为比例系数），就会导致χs(ωi)=1。

步骤7：根据模型精度评估结果，调整步骤3 中间接测量模型的超参数，再依次进行步骤4～6，直到获得满足精度要求的结果。

2 基于卫星实测数据的间接测量方法验证

2.1 数据集和相关性分析

为研究所用间接测量方法在卫星结构检测中的可行性，对生产线I 型卫星结构进行了x、y、z三个方向的正弦扫频模型振动试验，提取测点处的加速度频域响应。在I 型卫星结构表面（外部）选取了102 个加速度测点，在结构内部（内部）选取了24 个加速度测点，每个测点拥有x、y、z三个方向的加速度响应数据通道。图3 为振动方向为x方向、振动量级为0.15g的正弦扫频试验下某2 个测点的加速度幅频特性曲线。

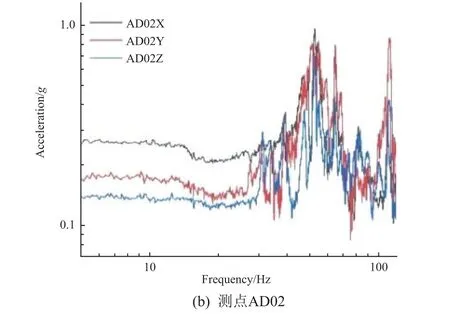
图3 某2 个测点的加速度幅频特性曲线（I 型卫星）Fig.3 Curves of frequency characteristic of acceleration amplitude at two measurement points (satellite I)

由于生产线I 型卫星的试验方案暂不成熟，测点布局方案处于初步选取阶段，为进一步验证所用间接测量方法的可行性与精度，对拥有成熟测点布局方案的II 型卫星结构进行了相同的试验，提取测点处的加速度频域响应。在II 型卫星结构表面（外部）选取了54 个加速度测点，在结构内部（内部）选取了32 个加速度测点，图4 为振动方向为x方向、振动量级为0.2g的正弦扫频试验下某2 个测点的加速度幅频特性曲线。

图4 某2 个测点的加速度幅频特性曲线（II 型卫星）Fig.4 Curves of frequency characteristic of acceleration amplitude at two measurement points (satellite II)

由试验结果可以看出，无论是I 型卫星还是II 型卫星，各测点响应数据间存在着较强的非线性和测试噪声的影响。为了对内部测点响应进行高精度反演，首先通过皮尔逊相关性分析依次针对每个内部测点进行外部测点的选取研究。X与Y两者间的皮尔逊相关系数为

式中：cov(X,Y)为数据X与数据Y之间的协方差；σX和σY分别为数据X与数据Y的标准差。以振动方向为x方向、振动量级为0.15g的正弦扫频试验为例，图5 给出了内外部测点响应之间的相关性图谱，其中横坐标为外部测点数据，纵坐标为内部测点数据，图中第i行第j列代表第j个内部测点数据与第i个外部测点数据的相关性，其数值用颜色表示，当相关性从小到大（ρX,Y从0 到1）时，颜色变化为从蓝到黄。根据相关性分析结果，针对每个内部测点，提取与其相关性最大的10 个外部测点数据建立反演模型。

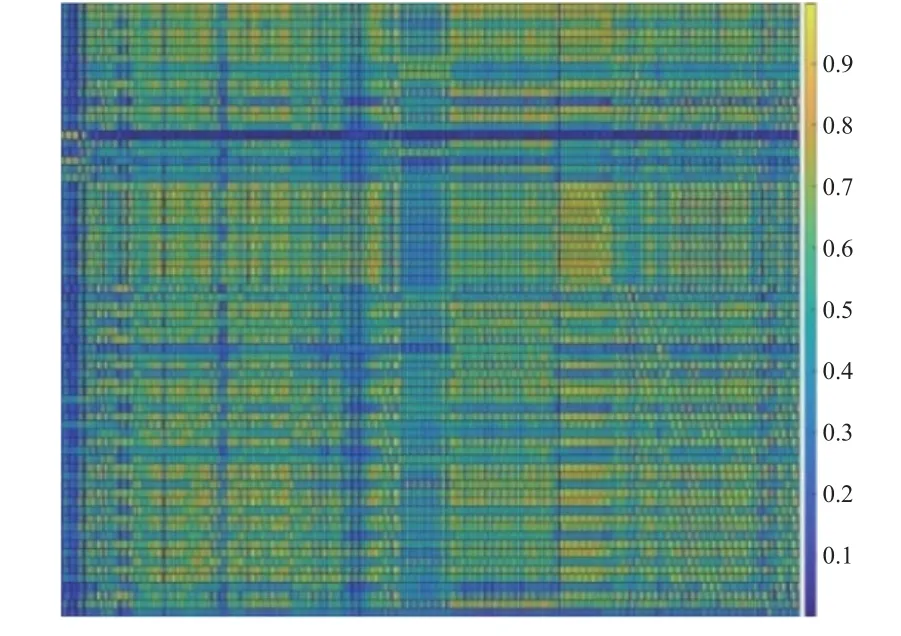
图5 内外部测点响应相关性图谱Fig.5 Correlation spectra of responses of internal and external measurement points

2.2 间接测量模型建立

针对I 型卫星，建立其在振动方向为x方向、振动量级为0.15g的正弦扫频试验条件下的内部测点响应间接测量模型：共有7 次正弦扫频试验数据用于间接测量模型的建立，选取前6 次试验数据作为训练集与验证集，第7 次试验数据作为测试集。

针对II 型卫星，建立其在振动方向为x方向的正弦扫频试验条件下的内部测点响应间接测量模型：共有3 次正弦扫频试验数据用于间接测量模型的建立，其中振动量级为0.2g的试验数据2 组，量级为0.6g的试验数据1 组，选取第1 组0.2g试验数据与0.6g试验数据分别作为训练集与验证集，第2 组0.2g试验数据作为测试集。

针对每个内部测点，都建立一个间接测量模型用于测量该测点的加速度幅频曲线。其中，模型输入为所选取的10 个外部测点响应数据，数据维度为10；模型输出为内部测点响应，数据维度为1。针对I 型卫星24 个内部测点的72 个数据通道，共建立72 个反演模型；针对II 型卫星32 个内部测点的96 个数据通道，共建立96 个反演模型。以I 型卫星内部测点通道AZ20X（AZ20 为测点编号，X 代表该数据为x方向的加速度幅频数据）为例，图6给出了深度学习模型的训练过程，可以看出，整个模型可以很快收敛到代价函数为0 的程度，说明该模型的建立较为合理。

图6 深度学习模型训练过程Fig.6 Training process of the deep-learning based model

2.3 结果分析

图7 和图8 分别给出I 型卫星测点通道AZ20X、AZ21X 与II 型卫星测点通道LA1X、LA2X 的间接测量与实际测量结果对比。可以看出，间接测量的反演结果与实际测量结果基本一致，说明该模型预测结果较为准确。

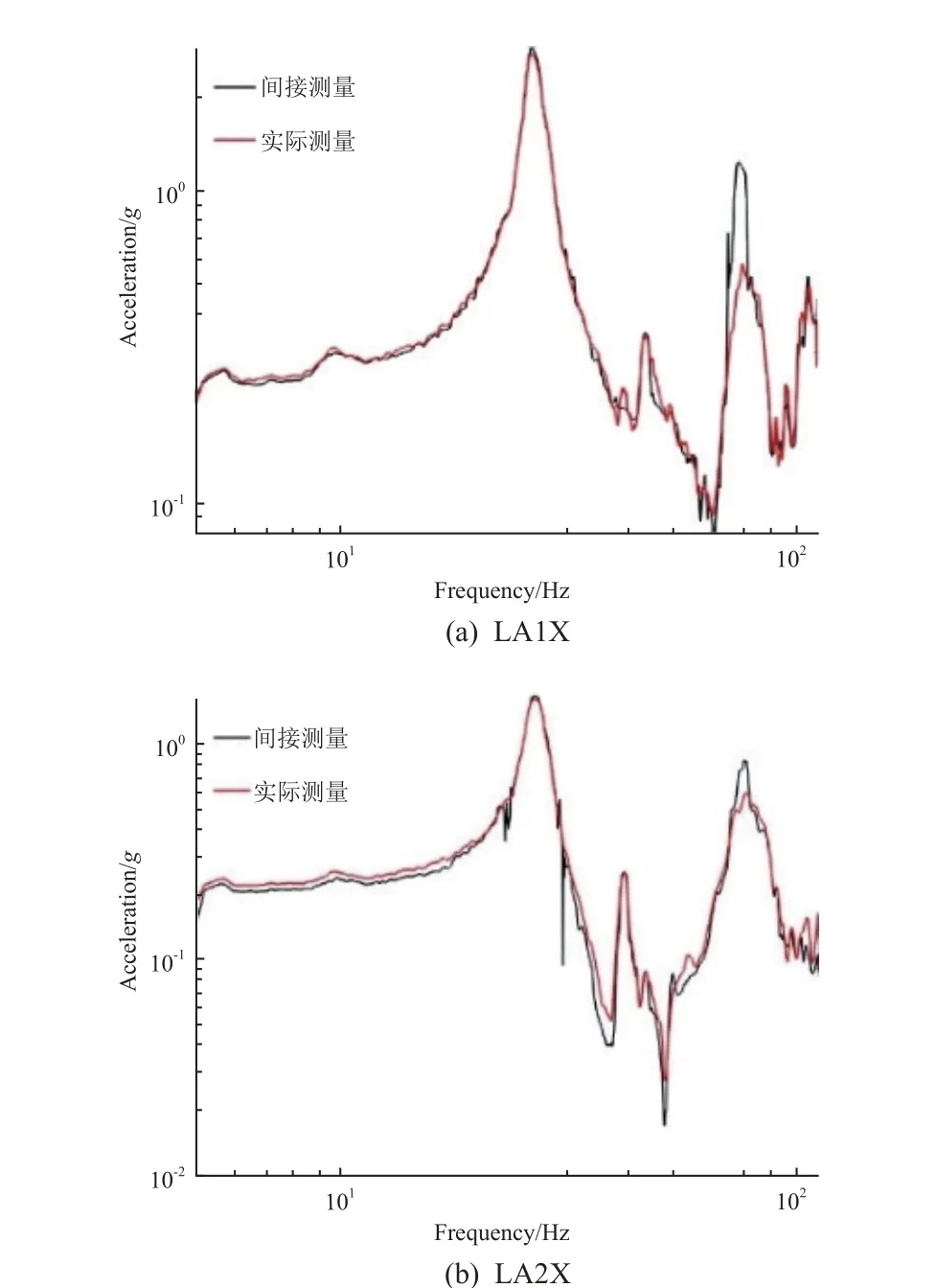
图8 间接测量与实际测量结果对比（II 型卫星）Fig.8 Comparison between indirect measurement and actual measurement results (satellite II)

同时，图9 与图10 分别给出了I 型卫星测点通道AZ20X、AZ21X 以及II 型卫星测点通道LA1X、LA2X 的间接测量和实际测量结果对比及相关性。可以看出：I 型卫星两测点通道间接测量与实际测量结果的相关性分别达到99%和98%；II 型卫星两测点通道间接测量与实际测量结果的相关性均达到99%。

图9 间接测量与实际测量结果对比及相关性（I 型卫星）Fig.9 Comparison and correlation of indirect and actual measurement results (satellite I)

图10 间接测量与实际测量结果对比及相关性（II 型卫星）Fig.10 Comparison and correlation of indirect and actual measurement results (satellite II)

若通道数据的间接测量与实际测量结果间曲线相关性大于0.9，则表明该通道满足间接测量的精度要求。I、II 型卫星间接测量数据的精度分析结果分别如图11 与图12 所示，图中黄色为未满足精度要求的通道，蓝色为满足精度要求的通道。

图11 I 型卫星间接测量数据精度分析结果Fig.11 Precision analysis results of indirect measurement data for satellite I

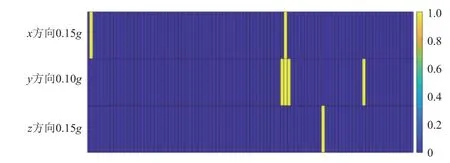
图12 II 型卫星间接测量数据精度分析结果Fig.12 Precision analysis results of indirect measurement data for satellite II

由图11 可以看出，对于I 型卫星，x方向、0.15g正弦扫频试验有 2 个测点通道（AD01Z、AD02Z）未满足精度要求；y方向、0.10g正弦扫频试验有 1 个测点通道（AD03X）未满足精度要求；z方向、0.15g正弦扫频试验有 5 个测点通道（AD02Y、AD03X、AD03Y、AD03Z、AG04X）未满足精度要求。归纳最终结果为：有4 个内部测点（AD01、AD02、AD03、AG04）的间接测量结果未满足精度要求，而其余20 个内部测点均满足精度要求，内部测点间接测量的成功率为83.3%。

由图12 可以看出，对于II 型卫星，x方向正弦扫频试验有 4 个测点通道（LA1Y、LA11Y、PA11Y、PA11Z）未满足精度要求；y方向正弦扫频试验有4 个测点通道（PA11X、PA11Y、PA11Z、PA21X）未满足精度要求；z方向正弦扫频试验有 1 个测点通道（PA17X）未满足精度要求。归纳最终结果为：有5 个内部测点（LA1、LA11、PA11、PA17、PA21）的间接测量结果未满足精度要求，而其余22 个内部测点均满足精度要求，内部测点间接测量的成功率为81.5%。

若只考虑主振方向或考虑所有方向，I 型卫星与II 型卫星的间接测量精度分析结果分别如图13与图14 所示。

图13 只考虑主振方向与考虑所有方向的间接测量精度对比（I 型卫星）Fig.13 Comparison among indirect measurement accuracy in main vibration direction only and in all directions(satellite I)

图14 只考虑主振方向与考虑所有方向的间接测量精度对比（II 型卫星）Fig.14 Comparison among indirect measurement accuracy in main vibration direction only and in all directions(satellite II)

由图13 可以看到，当将主振方向与非主振方向的间接测量结果都纳入精度评估范围时，I 型卫星x、y、z三种振动方向试验的精度分别为95.8%、97.9%和91.6%，内部测点间接测量总体精度为83.3%。当只考虑主振动方向的间接测量结果时，x、y、z三种振动方向试验的精度分别为100%、100%和95.8%，内部测点间接测量总体精度为95.8%。

由图14 可以看到，当将主振方向与非主振方向的间接测量结果都纳入精度评估范围时，II 型卫星x、y、z三种振动方向试验的精度分别为93.8%、95.4%和98.5%，内部测点间接测量总体精度为81.5%。当只考虑主振动方向的间接测量结果时，x、y、z三种振动方向试验的精度分别为100%、96.9%和100%，内部测点间接测量总体精度为96.9%。

3 结束语

本文针对生产线卫星力学试验步骤烦琐且内部结构响应测量困难，无法满足卫星脉动式快速生产需求的问题，提出使用深度学习方法建立结构外部响应与内部响应间的映射关系模型，通过外部可测的响应对内部响应进行间接测量。为验证所建立模型的合理性和精度，对生产线I 型卫星与成熟的II 型卫星进行了x、y、z三个方向的正弦扫频振动试验，获得了内外部测点的加速度频域响应数据；数据分析显示，当只考虑主振方向间接测量结果时，两种型号卫星的间接测量总体精度分别达到了95.8%与96.9%，表明本文所提出的间接测量方法具有较高的可行性与精度，可推广应用于结构的优化设计、减振隔振设计和结构健康监测等诸多领域，具有广阔的工程应用前景。

受限于大量级试验数据量上的缺乏，文中给出的间接测量例证针对的是小量级卫星动力学试验。待积累相同或相似卫星结构的大量级动力学试验数据后，会考虑构建大量级试验的间接测量模型。