基于GA-PS的三维空间源项反演算法
2023-09-07陈松朱东升左钦文韩朝帅
陈松, 朱东升, 左钦文, 韩朝帅
(军事科学院 防化研究院, 北京 102205)
0 引言
由于大国之间博弈以及中小国家间的利益冲突所导致的传统核生化威胁依然存在且持续显现。同时,以次生核生化危害、核生化恐怖活动和工业核生化事故为主要代表的非传统核生化威胁,正日益加剧[1-3]。自从“9.11”事件后,全球各地恐怖袭击频现,给各国人民的生命安全带来了严峻挑战。2013年8月叙利亚大马士革东部郊区发生化学武器攻击事件,含有致命毒气的化学武器造成了300名以上平民的死亡。2015年8月12日,位于天津市滨海新区的瑞海公司危险品仓库发生火灾爆炸事故,事故爆炸总能量约为450吨TNT当量,造成重大人员伤亡和财产损失。2020年8月4日,黎巴嫩首都贝鲁特港口区发生巨大爆炸,爆炸接连发生两次,导致多栋房屋受损,玻璃被震碎,天上升起红色烟雾。造成至少190人死亡、6 500 多人受伤,3人失踪。化学危害事故发生后,如何能够快速确定危害源位置和源强,快速预测一定时间后的扩散浓度分布情况,对于辅助制定人员救治、防护、撤离方案,最大限度减少人员伤亡和财产损失有着重要意义。
近年来,通过在无人机上搭载化学传感器实施三维空间探测已经成为趋势,但通过三维空间探测数据进行源项反演的研究还很少。大量学者对化学危害事件的源项反演方面做了研究,包括使用差分进化算法[4]、神经网络算法[5-6]、粒子群优化算法[7]、卡尔曼滤波算法[8]、参数敏感性分析方法[9]以及遗传-单纯形耦合算法[10]等,Wang等[11]对多点源污染事件提出两步反演算法,但以上研究大都停留在了二维层面,或将危害源设置在地面或忽略危害源高度,或将监测点设置在地面,均未考虑三维空间情形。史阳[12]利用单纯形搜索算法对源高进行了反算,但在理论数据条件下,误差仍超过40%。陈增强[13]将模式搜索算法引入到源项反演中,然而仅对源强度一维参数进行了反算,后续研究中,其又完成了地面源项的反演[14],但仍未拓展到三维空间中。胡峰等[15]基于1958年美国草原SO2泄漏实验数据[16],使用人群搜索算法(SOA)[17]开展了三维条件下反演性能评估,但由于SOA是启发式算法,结果具有随机性,单一使用SOA反演结果误差较大。
在以往算法中,对此类问题求解相对困难,例如基于贝叶斯的反算方法,通过先验概率和似然函数求解后验概率,需要先知道先验概率才能求解,假设先验概率已知,每多加一个维度,目标函数均需要重新计算,维度较高时,可能存在无法求解的情况。
通过深入研究遗传算法和模式搜索算法在多参数条件下的反演机制,建立了一种混合优化方法,充分利用了遗传算法的全局寻优性能和模式搜索算法的局部寻优性能,探索了对源强及源三维空间位置的反算能力。在理论计算数据基础上,利用三维空间中随机分布点浓度,能够实现对源空间位置和源强的高精度反算,通过仿真数据和SF6实测数据验证了该算法的可行性。结果表明,该算法能够快速准确地利用三维空间探测数据反算出源项的三维空间最优解。
通过对源项的有效定位,为化学危害事件后续的扩散预测和危害区域精准防护提供了先决条件。
1 算法在三维空间中的设计与实现
1.1 遗传算法在三维空间中设计与实现
遗传算法是模拟大自然中生物进化原理,将自然选择和遗传学机理通过数学方式进行表达,通过对各参数段在定义域上进行合理划定,将各参数进行编码、匹配成统一的类似生物基因组一样的基因结构序列,利用选择、交叉、变异等操作在解空间中搜寻最优解,通过合理设计基因序列和选择、交叉、变异算法,能够实现对全域范围的搜索,较快地获得较好的优化结果。遗传算法已广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域[18]。
遗传算法流程如图1[19]所示。

图1 遗传算法流程图[19]
遗传算法在三维空间中求解的实现:
1)初始化变量。包括种群规模N、交叉概率CR、变异概率MR,确定适应度函数f(s),即观测数据与计算数据的差值平方和。
2)初始化种群。随机创建N个向量[x,y,He,Q],x、y为危害源坐标,He为危害源有效高度,Q为源强,由这N个向量构成一个N行的数组,也即N个基因结构序列。其中x、y、He、Q均在其定义域随机选定,x∈[0,max_x],y∈[-max_y,max_y],He∈[0,max_He],Q∈[0,max_Q]。
采用实数编码,种群初始化如下:
pop.individual=rand(N,4);%pop.individual=(x,y,He,Q)
pop.individual(:,1)=pop.individual(:,1)*max_x;%(0,max_x)
pop.individual(:,2)=pop.individual(:,2)*max_y-rand( )*max_y;%(-max_y, max_y)
pop.individual(:,3)=pop.individual(:,3)*max_He;%(0, max_He)
pop.individual(:,4)=pop.individual(:,4)*max_Q;%(0, max_Q)
式中:rand( )函数产生由(0,1)之间均匀分布的 1个随机数,rand(N,4)产生由(0,1)之间均匀分布的N行4列个随机数。
3)计算适应度。将N个s=[x,y,He,Q]分别代入f(s),得到各自的适应度值f1,…,fN,值越小表明适应度越高。记录最优个体s=[x,y,He,Q]。
4)选择操作。计算每个个体的生存概率p=(sum(f1,…,fN)-fi)/sum(f1,…,fN)。
利用累计概率或轮盘赌的方式进行选择操作。
以7个个体为例使用轮盘赌,如图2所示。有7个个体组成的种群,每个个体的生存概率如图2所示(f1的概率为θ/360°=59.84°/360°=16.6%,其他类推),利用随机函数rand( ),依次生成[0,1]内的7个随机数r,落在哪个区域,则哪个fi值对应[x,y,z,Q]保留,未落入的区域则被淘汰。适应度函数所对应的生存概率越大,被选择保留的概率越大,相反,越不理想的值,生存概率越小,淘汰概率越大,即生物进化中的适者生存。

图2 轮盘赌
由选择操作,生成了新的种群,N个[x,y,He,Q]的数组,适应度低的个体被淘汰,适应度高的个体被选中,选中后的个体进行基因复制替换掉被淘汰的个体。
5)交叉操作。将N个[x,y,He,Q]的数组看成N个行向量,可以随机选取任意两个进行交叉操作,也可将N个行向量从第1行到第N行,进行两两配对(假设N为偶数,N为奇数时,最后落单的不处理)。
假设A是第1行个体,B是第2行个体。
随机生成一个[0,1]的随机数r=rand( )。如果r小于交叉概率CR,则将A和B进行交叉操作,如果r大于交叉概率CR,A和B不进行交叉操作,继续对后续三、四行进行同样判断。
交叉操作实现:指定随机交叉点,生成[0,1]内的随机数p=rand( )。假设交叉后新个体分别为A1、B1。则A1=pA+(1-p)B,B1=pB+(1-p)A。
6)变异操作。对步骤5生成的新的N个[x,y,He,Q]个体,依次执行以下操作。
随机生成一个[0,1]的随机数r=rand( )。如果r小于变异概率MR,则将个体[x,y,He,Q]进行变异操作,如果r大于变异概率MR,则不进行变异操作。
变异操作实现:
随机生成一个数n∈{1,2,3,4},n取1~4中一个数,假设n=3,则对He进行变异,相当于变异位置在He。
生成一个标准正太分布随机数q=randn( )。假设He的取值范围为[0,max_He],则变异后的He=He+q·max_He。为防止变异后,He值超出取值范围,约定He<0时,He取0,He>max_He时,He取max_He。
7)终止条件判断。完成变异操作后,生成新的种群N个[x,y,He,Q]。此为一轮遗传算法,将新生成种群,作为输入,重复执行以上操作步骤,直到到达指定的循环次数K,循环结束。最终生成的N个[x,y,He,Q]即为最后的种群,其中适应度值fi最小的D=[x,y,He,Q]的即为所求最优个体,D即遗传算法的输出值,也是输入给模式搜索算法的初始值。
1.2 模式搜索算法在三维空间中设计与实现
模式搜索法[20]是一种直接搜索优化方法,该方法通过直接计算目标函数值来调整优化,而不需要求解梯度信息。该方法主要包括两个步骤,即轴向探测和模式移动,首先通过轴向探测寻找到目标函数的下降的有利方向,进而利用模式移动沿着有利方向加速搜索。
算法从初始基点开始,交替实施两种搜索:轴向搜索和模式搜索。轴向搜索依次沿n个坐标轴的方向进行,用来确定新的基点和有利函数值下降的方向。模式搜索则沿着相邻两个基点的连线方向进行,试图使函数值下降更快。
模式搜索算法流程如图3所示。
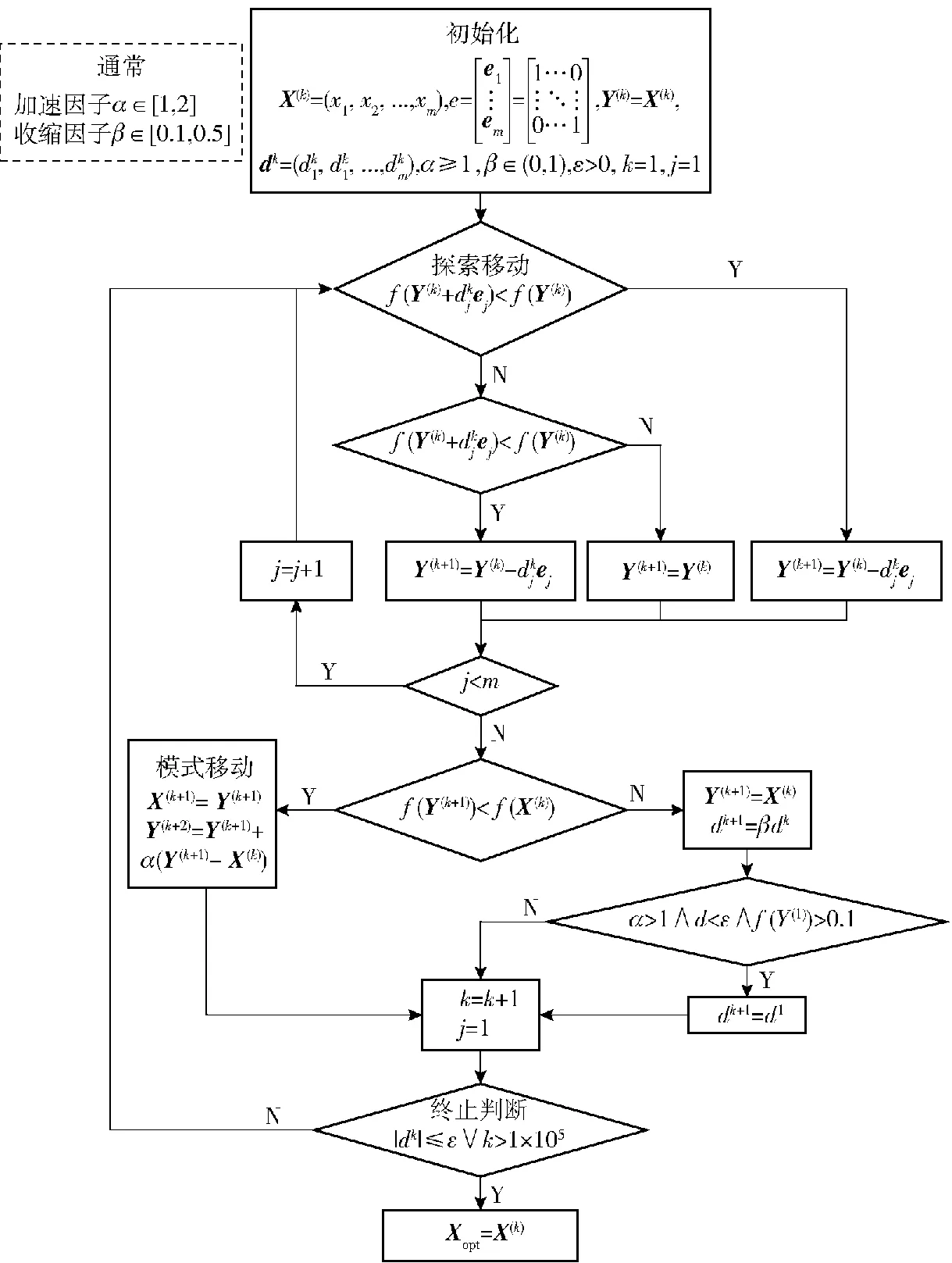
图3 模式搜索算法源强反算流程
模式搜索算法在三维空间中求解的实现:
1)初始化变量,给定初始点X=[x,y,He,Q],令下一探测点Y=X,初始化加速因子α、收缩因子β、步长d=[d1,d2,d3,d4]、算法精度ε,适应度函数f(X),轴向探测循环控制变量j=1,模式探测循环控制变量k=1。构造探测向量e,即
2)如果f(Y+djej) 3)如果f(Y-djej) 4)根据源项实际,高度He和源强Q不得小于0,因此,如果Y(3)<0,令Y(3)=0,即He=0,如果Y(4)<0,令Y(4)=0,即Q=0。 5)如果j<4,则置j=j+1,转步骤2,否则,进行步骤6。 6)如果f(Y) 7)置Temp=Y,令Y=Y+α(Y-X),X=Temp,置k=k+1,j=1,转步骤2。 8)令Y=X,d=βd,置k=k+1,j=1。 9)为防止加速因子过大时,导致步长减小过快,无法继续搜索,当α>1时,需判断:如果d<ε,f(Y)值仍较大时,应恢复初始步长,置d=[d1,d2,d3,d4]。 10)如果d≤ε或k>1×105,则停止迭代,得到点X并输出,否则,转步骤2。 遗传算法是一种优异的全局搜索算法,通过对求解参数进行基因编码,实现在全域解空间中进行搜索,通过种群数量设置,能够实现并行搜索能力。但由于搜索的随机性,每次得到的解也是随机变化的,导致遗传算法的搜索精度受限,只能搜索到可行解洼地,而无法寻找到最优解。 模式搜索算法通过轴向探测和模式移动,不断向有利于目标函数值下降的方向探索,在规定精度内能够求得当前解洼地内的最优解。模式搜索算法对初值敏感,在步长和加速因子较小的情况下,全局寻优性能较差,但由于收缩因子的控制,局部搜索能力较为优异。 遗传算法和模式搜索均是通过对各参数在其定义域内进行搜索,不需要进行求导、求梯度运算,因此,在处理高维度寻优中具有极大优势,每增加一个维度,仅是在基因编码中增加一个基因片断,整体算法不会有较大改变。相较贝叶斯等算法,该算法求解速度快,实现简单,增加维度情况下,代码修改量较小,适合维度的拓展。 因此,通过将遗传算法和模式搜索算法进行结合,能够充分发挥两种算法的优点,求得全局最优解。但是,由于遗传算法存在早熟问题以及求解过程中的随机性,直接使用两种算法求解并不稳定,有概率落入局部最优解中。因此,本文提出一种基于遗传算法-模式搜索算法的MGAPS算法,可以克服该缺点,保证了算法求解的稳定性。 MGAPS算法设计流程(见图4)为: 图4 MGAPS算法设计流程图 1)初始化相关参数,令j=1、i=1,向量A用于存放结果向量,矩阵M用于存储由向量A组成的结果矩阵,A=[f,x,y,He,Q],其中f是适应度函数值,Q是源强度,[x,y,He]分别是源的横、纵坐标和高度。 2)执行遗传算法,求得一组初始解,存入矩阵T(j,:)=[x,y,He,Q]中,矩阵T的每一行即一组初始解。 3)若j≤L,则令j=j+1,返回步骤2,否则转步骤4。 4)对求得的L组初始解的每列求均值后形成一个新解向量,即QX=sum(T)/L。 5)将QX作为初始基点,执行模式搜索算法,求得解X=[x,y,He,Q]。 6)计算解X的适应度函数f(X),将求得的值f与解向量X组合成新的向量存入向量A中,即A=[f,x,y,He,Q]。 7)将解向量A作为解矩阵M的一个行向量存入矩阵M中。 8)若i≤K,则令i=i+1、j=1,返回步骤2,否则转步骤9。 9)将解矩阵M中适应度值f最小的一行解赋值给变量Obj,即Obj=min(M(f)),算法终止,Obj(2∶5)即为所求最优解。 遗传算法是随机算法,能够找到最优解洼地,但也有一定概率找到局部最优解,这种概率通过增加种群可以降到很低,几乎可以忽略,但为了防止这种小概率事件,通过设计多次循环,优中选优的方式,保证了求解结果在最优解附近,且是最近的解,将该解作为模式搜索算法的输入,可以提高算法的准确性和运行效率。 构建化学事件危害场景,为后续源项反演分析提供基础。对连续泄漏的化学危害源,利用高斯烟羽模型进行近似扩散模拟[21]: (1) 式中:C(x,y,z,He)是有效源高为He时(x,y,z)点的浓度;u为风速;σx、σy、σz分别为距离原点x处烟团中污染物在下风方向、侧风方向及垂直方向的扩散系数,也即高斯分布的在x轴、y轴、z轴方向的标准差。 为验证MGAPS的可行性,设置如下场景:1)在2 000 m×600 m范围内模拟危害源扩散;2)危害源强度Q=5×106g/s,位置为(30 m,50 m,10 m);3)大气稳定度为D级,相关参数设置见表1[22]所示;4)平均风速为2 m/s;5)在下风向5×6网络的三维空间中放置探测器,探测器高度可三维空间范围内任意随机选取,但考虑到实际应用中,无人机探测器数量较少,大部分探测器安装于手持仪器或探测车辆上,因此随机选取5个探测器置于在10~50 m 内随机高度,其余探测器位于1~5 m高度,如图5~图7所示。 表1 扩散参数[22] 图5 监测点位置俯视图 图6 监测点三维空间位置 图7 三维空间5 m随机高度下空间浓度分布 实验环境配置:处理器i5-9300H,主频2.4 GHz,内存8 GB。 (2) 设(xc,yc,Hec,Qc)为源项的预估值,由遗传算法或模式搜索算法提供,(xi,yi,zi)为第i个监测点的三维坐标。式(1)为源项横纵坐标位于原点时的计算公式,因此,(xi,yi,zi)点在以(xc,yc,0)为原点下的坐标为(x,y,z),坐标变换如下: (3) (4) 式中: (5) γ1、μ1、γ2、μ2分别为下风距离小于等于1 000 m时σy、σz的扩散系数,γ3、μ3、γ4、μ4分别为下风距离大于1 000 m时σy、σz的扩散系数。式(5)中(x,y,z)由式(3)求得。 表2 监测点观测值浓度 计算每个监测点观测值与计算值的差值平方和,之后,再对所有监测点的差值平方和进行求和,即 (6) 所有可能的解中(x,y,He,Q),使得式(6)最小的解为所求,即式(2)所示。 遗传算法有4个超参数需要设置[23],即: 1) 种群规模N(N≥1):规模太大会增加计算量,规模太小无法提供足够多的样本数量。一般取为20~100。 2) 终止代数T(T≥1):代数太大会导致运行时间过长,代数太小无法求得最优解。一般取为100~500。 3) 交叉概率CR(CR∈[0,1]):概率太大会使种群中的优异个体被破坏,概率太小会使搜索停滞不前。一般取为0.40~0.99。 4) 变异概率MR(MR∈[0,1]):。概率太大会变成随机搜索,概率太小则不会产生新的基因,导致早熟现象,陷入局部解。一般取为0.000 1~0.1。 模式搜索算法有4个超参数需要设置[24],即: 1) 加速因子α(α>0):因子太大会使模式移动过大,算法无法收敛,因子太小会使搜索停滞。一般取为1~2。 2) 收缩因子β(β∈(0,1)):因子太大会使步长变化缓慢,导致运行时间过长,因子太小会使步长迅速减小导致搜索过早结束,无法求得最优解。一般取为0.1~0.5。 3) 初始步长d(d>0):用于控制沿各轴向探测的步进长度,过大或过小都不利于遍历轴向搜索。一般取为1。 4) 算法精度ε(ε>0):用于控制模式搜索算法的结果精度,是模式搜索算法的终止条件之一,根据实际需要设置。 为保证MGAPS求解结果的准确性和算法运行效率,经过对以上各参数的反复调试验证,实现MGAPS算法在三维空间中的求解实现能力,得到算法参数设置如下: 1) 遗传算法参数设置:种群规模N=20,交叉概率CR=0.4,变异概率MR=0.1,终止代数T=100。 2) 模式搜索算法参数设置:加速因子α=1,收缩因子β=0.5,初始步长d=[1,1,1,1],算法精度ε=10-4。 采用实数编码,内循环执行L=20次,外循环次数K=10次,运行10次MGAPS算法,结果如表3所示。 表3 MGAPS算法运行结果 通过表3数据可以看出,MGAPS可以有效实现三维条件下源项信息的求解,但耗时较长,作为化学事件应急使用,应尽量减少计算耗时。因此,可以通过调整循环参数优化算法运行时间。不同循环次数下的计算结果如表4所示。 表4 不同循环次数下的运行效率及结果 通过表4可以看出,该算法随着循环次数的增加,耗时相应增加,但所有组合的结果均较为理想,因此,考虑针对事故应急使用,使用耗时1 min内的组合模式较为合理,即L=5、K=2或K=3,另外,考虑到遗传算法的随机性,循环次数较少时,容易出现落入局部最优解的可能,因此,选择L=5,K=3的组合。 在上述实验中,使用的测量数据是理论计算数据,较为理想,导致反演结果与设置值几乎一致。为了更加接近真实环境,通过对测量数据进行白噪声处理,再验证算法的反演性能。 3.3.1 对观测数据增加高斯白噪声 通过设置不同强度的信噪比,观察白噪声对计算精度的影响,结果如表5所示。 表5 不同信噪比下反演结果比较(L=5,K=3) 通过表5可以看出,随着信噪比的增加,计算结果更准确、精度更高,符合预期。但在低信噪比情况,算法解算效果同样较为理想。以上结果表明,在测量数据准确的情况,对于不同信噪比,本文算法皆能较好地完成对源项的反算。 3.3.2 降低观测数据观测精度 在前述实验中,所使用的观测数据为理论计算数据,精度到达了小数点后13位,因此,在加入高斯白噪声情况,对数据的影响效果不明显,导致在低信噪比条件下仍能得出较为理想的反算结果。但在实际环境下,所使用的测量仪器并不能达到如此高的测量精度,因此,通过降低观测数据精度,验证算法的反算性能,结果如表6所示。 表6 不同观测值精度下的反演结果比较(L=5,K=3) 通过表6可以看出,在使用理论计算数据情况下,通过降低小数点精度对计算结果的影响不大,这由于本算法采用的是循环迭代算法,并从结果组中搜寻使适应度函数值最小的值作为最优解输出,因此在多轮迭代后,总能找到最优解,通过以上测试验证了这一特点,因此,本文算法具有较强的抗干扰能力,确保了算法寻优的稳定性。 以L=5、K=3及未添加噪声的计算数据为例,演示坐标、浓度的反算变化过程,如图8~图12所示(同一颜色*号数据为对应同一次外循环K下的遗传算法求解值) 图8 第1次遗传算法求解 图9 第2次遗传算法求解 图10 第3次遗传算法求解 图11 第4次遗传算法求解 图12 第5次遗传算法求解 图8~图12显示了5次利用遗传算法求解源三维空间坐标及源强的过程,从图中可以看出,遗传算法在求解过程中,结果具有随机性,个别值误差较大,但大多数以期望值为中心波动。为了降低个别异常误差对结果的影响,通过将5次计算结果求取算术平均值,则能够保证结果落入最优解洼地中,将该结果作为模式搜索算法的初值,即可求得精确解。但为了防止小概率落入局部最优解中,通过执行3次外循环模式搜索算法,并取其中1次最好解作为最终解输出,保证了结果的正确、稳定,消除了随机性造成的误差,如图13所示。 图13 模式搜索算法求解 从图13中可以看出,遗传算法搜索到最优解洼地后,在不同初值条件下,模式搜索算法均能够收敛于期望值附近,实现了对三维空间坐标及源强的反算。将图13中的x、y、He值进行合成,形成3次模式搜索算法对源位置的三维空间寻优过程,如图14所示。 图14 模式搜索算法空间寻优过程 从图14中可以看出,利用5次遗传算法求均值得到的初值位置在一定空间范围内波动,尚不准确,经过模式搜索算法进一步寻优,能够收敛于最优值。 在第3节中,使用的观测数据为理论计算数据,反算结果较为理想。在本节中,以2016年于华北某地开展的SF6示踪试验为例,利用实测采集数据,进行源项参数反算,验证算法的求解性能。 六氟化硫,化学式为SF6,无色、无毒且常温下化学惰性、光照稳定的气体,难溶于水、在大气中天然本底低(1×10-15m3/m3)、不沉降、能与周围空气迅速混合,能充分代表大气运动,用电子俘获气相色谱可获得2×10-13mg3/m3的高灵敏度,是一种较理想的示踪剂,其示踪距离可远达100 km[25]。 大气扩散示踪试验为期6 d,在气象铁塔100 m高度(30 m高度为辅)释放示踪剂SF6,共进行了23次 释放,采样56次,试验期间风速变化大(风速为0.5~7.9 m/s),试验覆盖多种天气类型(大气稳定度类型为B、C、D),释放情况如表7所示。 表7 SF6示踪实验与模拟条件 试验共布设弧线7条,采样点50个,距地面高度1.6 m,分别为A、B、C、D、E、F和G组,分别负责下风向不同距离的采样,各组采样点数如表8所示。试验区域地形平坦,但由于试验区域附近地形地貌影响,导致布点位置不是弧形,如图15、图16所示为第1次释放采样点位置。 表8 采样点编组 图15 第1次释放第1次采样有效采样点位置 图16 第1次释放第1次采样有效采样点位置(调整x轴正向为下风方向) 23次有效试验,每次的有效样品采集率如表9所示。在整个试验中,共采集有效样品1 633个,每次布设50个点采样,时间同步采样。除了第9次(由于释放高度风速为0.5 m/s)释放获取率为35.5%较低外,其他22次都超过了一半,总有效样品采集率为58.8%。 表9 各次试验有效样品采集率 4.2.1 实验参数设置 遗传算法:种群规模N=20,变异因子MR=0.95,交叉概率CR=0.5,进化代数I=100,外循环次数K=10,内循环次数L=10。 模式搜索算法:加速因子α=1,初始步长d=[1,1,1,1],收缩因子β=0.5,算法精度ε=1×10-4。 坐标参考系:以释放铁塔为原点,以下风向为x轴正方向,以下风向逆时针旋转90°为y轴正方向,在2 400 m×7 000 m范围内布设监测点。 4.2.2 算法反算求解 利用算法对56组数据进行反算,结果如图17~图24所示。 图17 源强反演结果 图18 源高反演结果 图19 横纵坐标反演结果 图20 源位置反演结果 图23 横坐标反演相对误差 图24 纵坐标反演相对误差 图17~图24分别是源强、源高、横纵坐标和源位置的反算求解结果与真值的对比图以及各参数的相对误差(横纵坐标相对误差采用求解值与相应坐标轴范围的比值)。从结果来看,MGAPS算法能够对56组实测数据中的大部分进行解算,偏差大多数在100%以内,尤其是前30次的反算结果与真值的一致性较好,偏差大部分在30%以内,这主要是由于大气环境波动造成的(见表7),第5天和第6天,大气稳定度以B级别为主,为不稳定状态,大气层结不稳定,热力湍流发展旺盛,对流强烈,对探测数据的采集有较大影响。 4.2.3 模型评价分析 针对模型有效性的验证,Chang 等[26]提出利用了统计误差分析方法,该方法被广泛应用于大气扩散模型的评价中。 统计误差分析方法包括:比例偏差SFB、几何平均偏差SMG、几何平均方差SVG、标准化均方误差SNMSE、相关系数SCOR以及SFAC2等统计误差[24, 26-28]。 SFAC2表示预测浓度与实测浓度之比在0.5~2.0之间的预测数据占总数据的比值。 各统计误差表达式分别为 (7) SMG=exp(E(lnCo)-E(lnCp)) (8) SVG=exp(E((lnCo-lnCp)2)) (9) (10) (11) 从统计分析看,以上误差的理想取值分别是:SFB=0,SMG=1,SVG=1,SNMSE=0,SCOR=1,SFAC2=1。Chang等[26]通过对大量扩散模型结果与观测结果对比,认为可接受的模型应满足:-0.3≤SFB≤0.3,SNMSE<4,SFAC2>0.5,SCOR>0.7,0.7≤SMG≤1.3,SVG≤4。 以上统计参数的选择条件:当Co与Cp的值分布在一个很大范围时,SFB、SNMSE和SCOR受Co或Cp中较大值的影响大,受较小值的影响小。为了公平衡量这些数据的作用,推荐使用对数统计量SMG、SVG。当实测值与预测值分布范围不大时,应使用SFB、SNMSE、SFAC2和SCOR。本文属于后者,因此不使用SMG、SVG。 利用MGAPS算法模型预测数据与实际数据进行比对,实测浓度与预测浓度散点图如图25所示,在监测点浓度值对比如图26所示。 图25 实测浓度与预测浓度散点图 图26 预测浓度与实测浓度在监测点的对比 图25显示了实测浓度与MGAPS模型预测浓度的散点分布,从图中可以看到数据点相对集中均匀地分布在红线的两侧(实测浓度=预测浓度),说明模型的预测结果与实测结果相关性较好。从图26中可以看出,实测浓度与预测浓度的总体趋势相同,符合扩散预期特征。 利用式(7)、式(10)、式(11)和SFAC2,进一步对二者进行统计误差分析,评价模型的有效性,得到结果如表10所示。 表10 MGAPS算法预测值统计误差 从表10中可以看到,预测结果的统计误差都在可接受范围之内,因此,MGAPS算法模型能够较为准确的预测气体扩散,并用于化学危害源的源强及三维空间坐标的反算求解。 4.3.1 误差原因分析 由实测数据反算实验可知,利用实际监测数据,通过MGAPS算法能够对在真实环境中的化学危害物质扩散后的危害源位置、浓度及释放源高度的反算求解,精确度在30%以内,但仍有部分解算误差较大,甚至无法求解的情况,主要原因有以下4个方面: 1)算法模型误差。MGAPS算法是通过利用理想状态下高斯扩散原理对污染物扩散进行求解,但真实环境中需要考虑的实际因素很多,此类误差可通过深化模型分析解决,但是不可能避免。在大气环境稳定状态下,算法求解较为理想,能够将误差精度控制在一定范围内。 2)监测仪器及测量误差。气象测量设备、示踪剂采样设备、示踪剂分析设备等测量偏差也是导致计算误差产生的原因,同时由于在测量过程中,采样点位置的选择,周围环境、遮蔽物等因素,也会导致测量误差的存在。 3)背景场误差。由于风向和风速对示踪气体扩散有较大影响,试验区域风向风速多变,示踪气体的扩散规律不稳定,导致测量结果差异较大。例如,第1天~第4天,大气稳定度多为C、D为主,大气环境稳定,反算结果较为理想,特别是在早上日出前后的测量数据反算效果较好。而第5天~第6天,大气层结不稳定,在地面的监测结果存在较大误差,导致求解偏差较大,甚至无法求解的情况。 4)重气扩散误差。本文使用理想高斯模型进行计算,适用于扩散机制较为清晰的中性气体,SF6扩散实验属于重气扩散,其扩散机制复杂,可能导致反算结果误差较大。下一步,可通过将目标函数更改为重气扩散模型进行反算性能验证。 4.3.2 算法适用性 通过以上实验分析,本算法在大气稳定度C及以下,风速、风向等大气环境条件稳定情况下,能够较好的对危害源相关参数的反算。但由于受限于采样条件,在大气稳定度为B及以上时,离危害源较远的地面监测点采样结果不理想,未来,可通过增加无人机等手段,通过对空中一定高度的浓度数据进行监测,并反算求解,进一步验证算法的可行性。 针对化学危害事件后,需要尽快确定危害源参数的现实需求,提出一种基于GA-PS的MGAPS算法,并进行了仿真分析。得出以下主要结论: 1)MGAPS算法基于三维空间探测器收集的危害物质浓度数据,能够实现对危害源在三维空间的定位和源强的反算。 2)当内循环执行20次、外循环执行10次时,误差不超过10×10-5要求下,MGAPS算法耗时约为177~323 s。 3)通过优化内循环执行次数与外循环执行次数的组合,可以大幅度提高运行效率。当内循环执行5次,外循环执行3次,误差不超过10×10-5要求下,耗时可在50 s左右,满足实用要求。 4)MGAPS算法具有较强的抗干扰能力,通过对观测数据增加高斯白噪声、降低观测数据精度等操作,算法均能稳定求解。 5)MGAPS算法能够针对大气稳定度C及以下,风速、风向稳定的大气环境条件下的实际监测数据进行反算,求解精度在30%以内,基本能够实现对危害源的有效定位。2 MGAPS算法实现
2.1 MGAPS算法实现思路
2.2 MGAPS算法设计

3 实验验证与分析
3.1 化学事件危害模拟场景

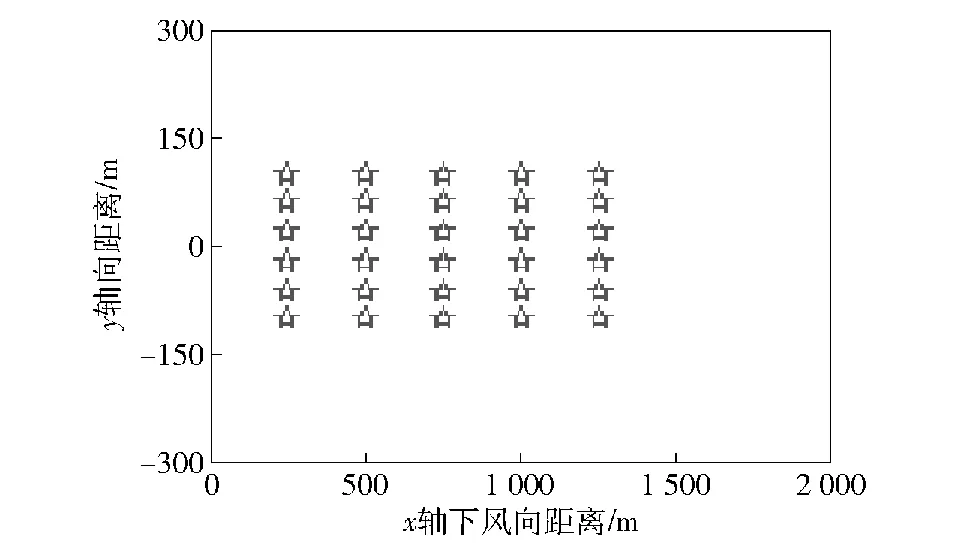
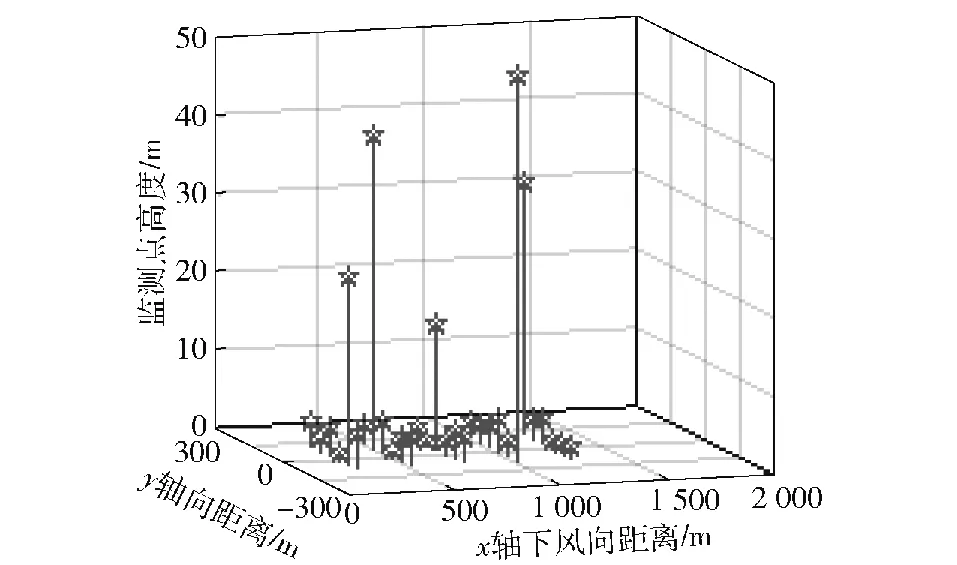

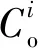
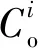

3.2 算法参数设置
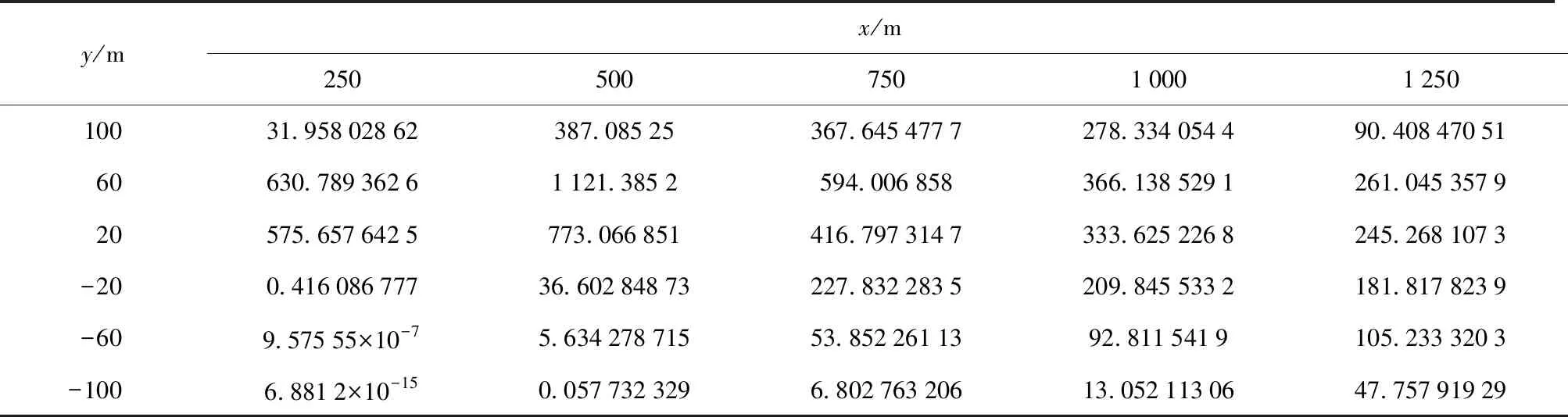
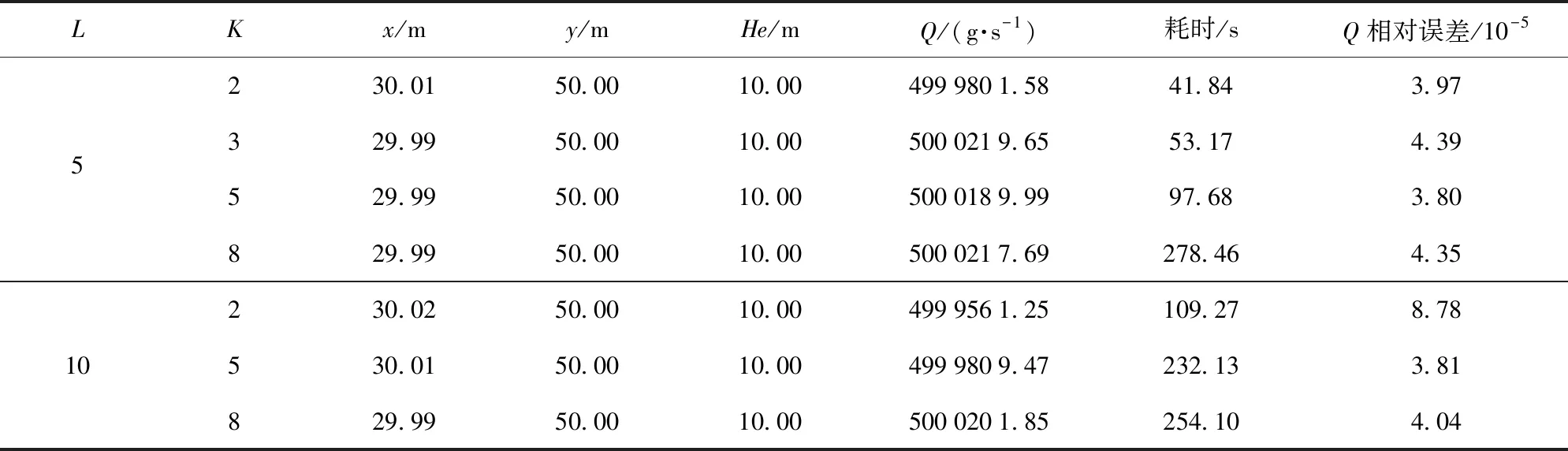
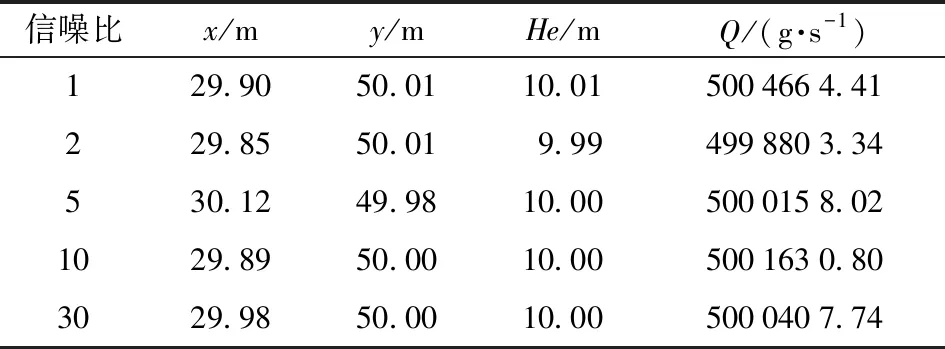
3.3 MGAPS算法求解

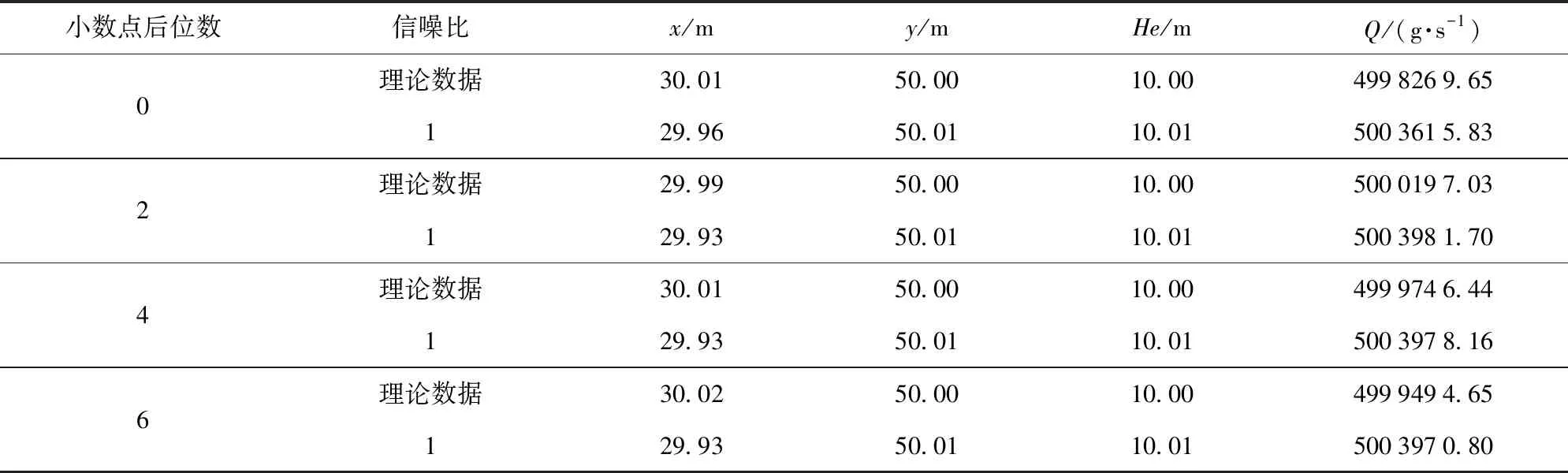
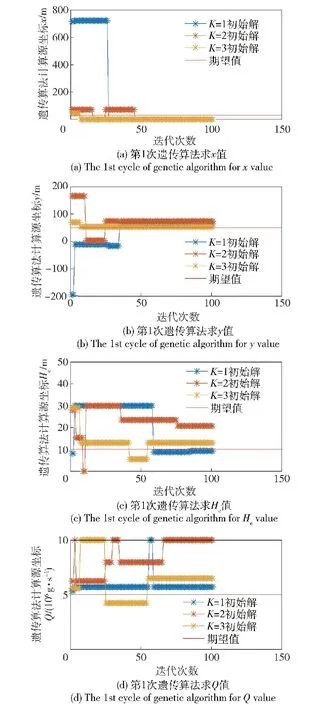

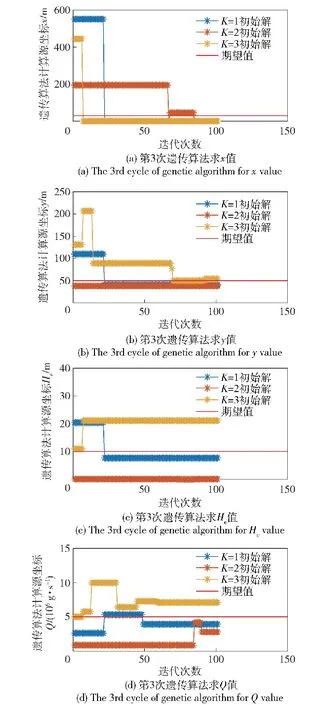
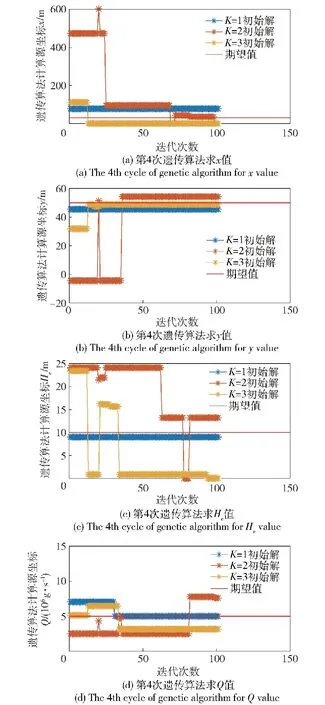
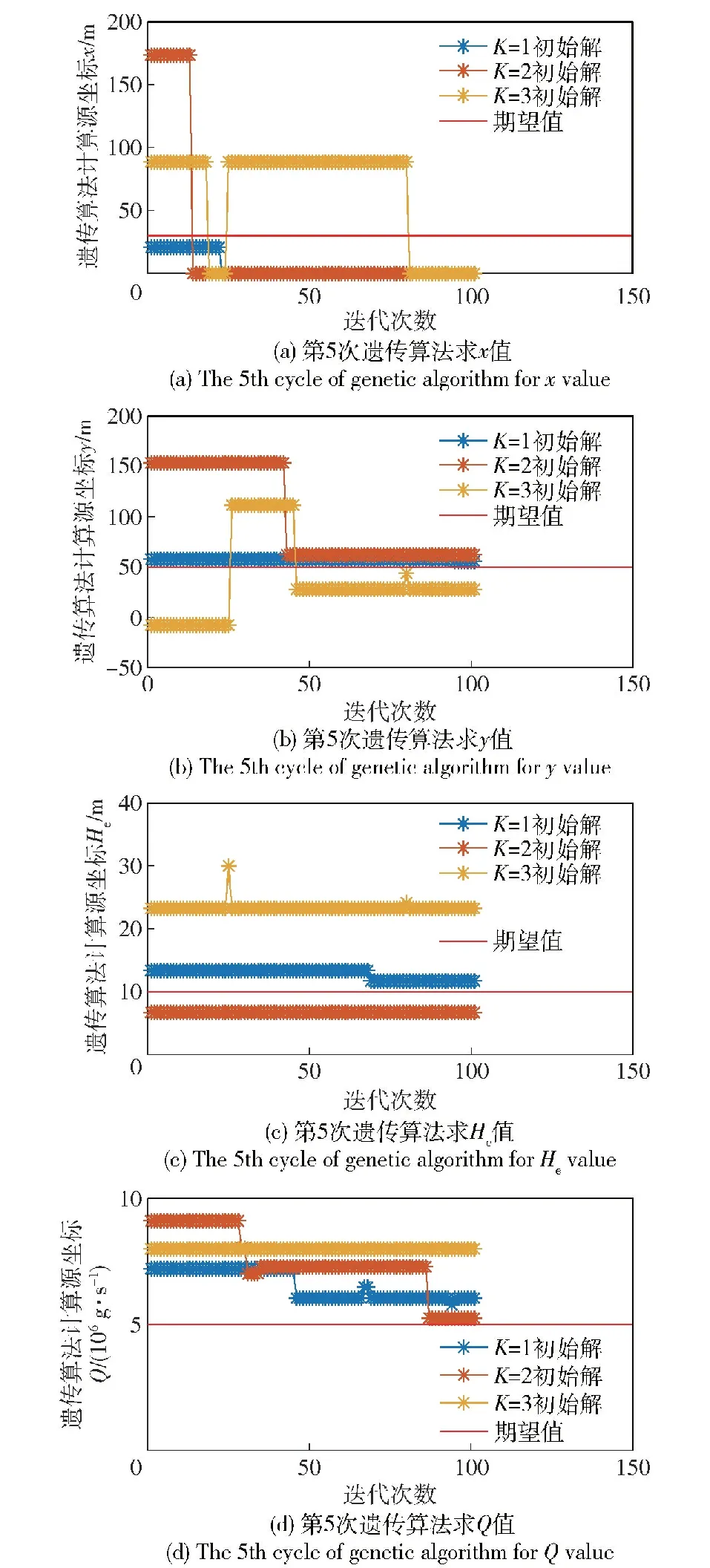


4 实例分析
4.1 SF6示踪实验基本情况介绍
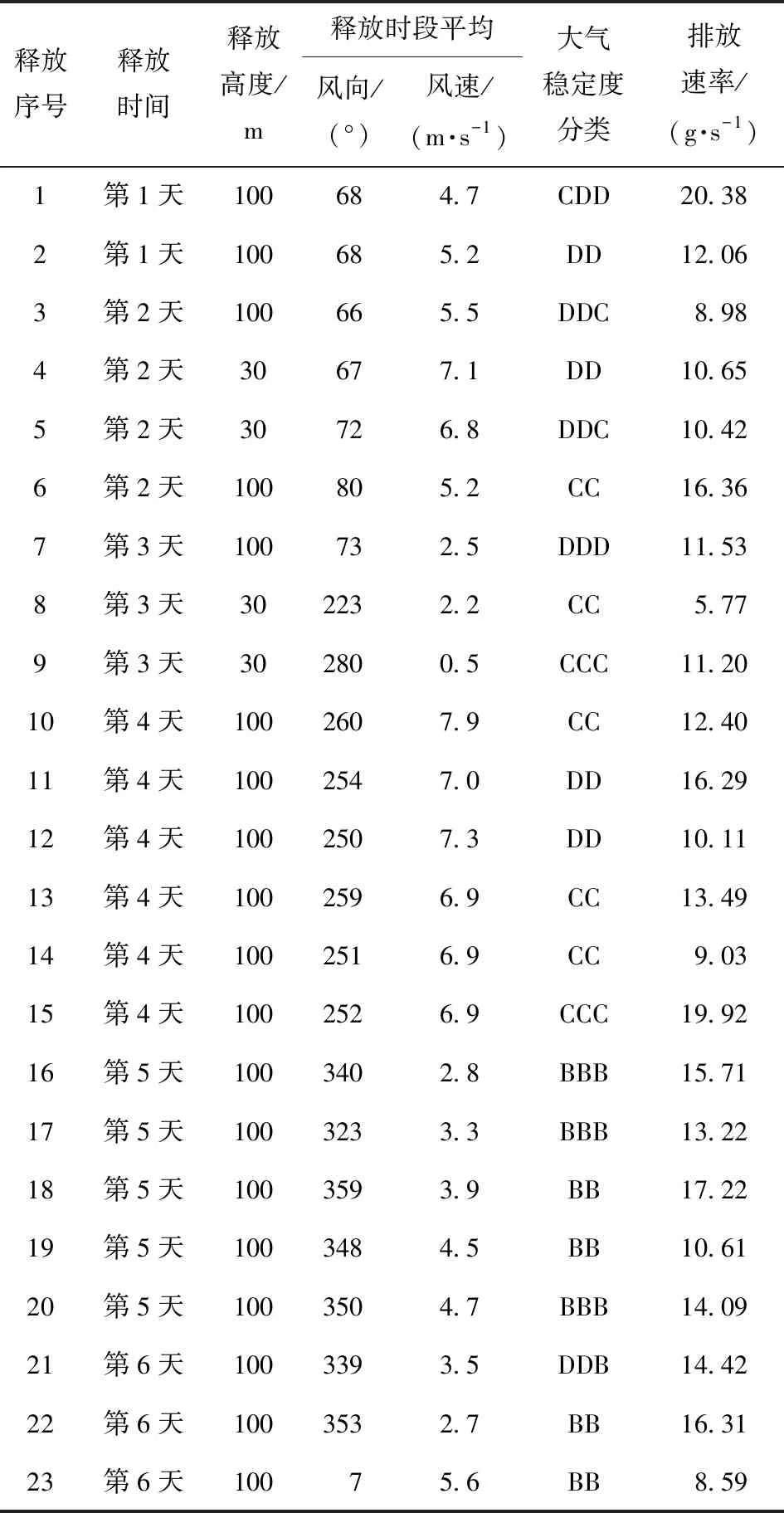
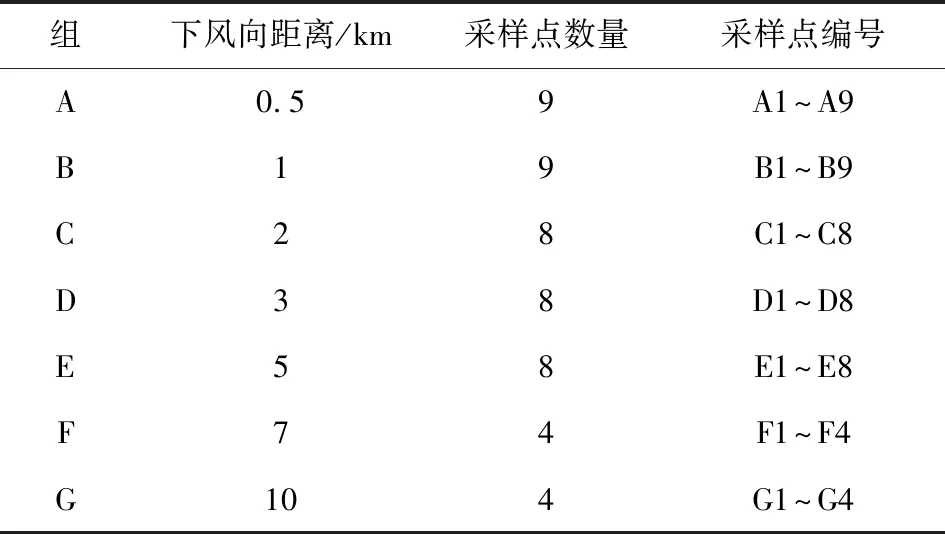


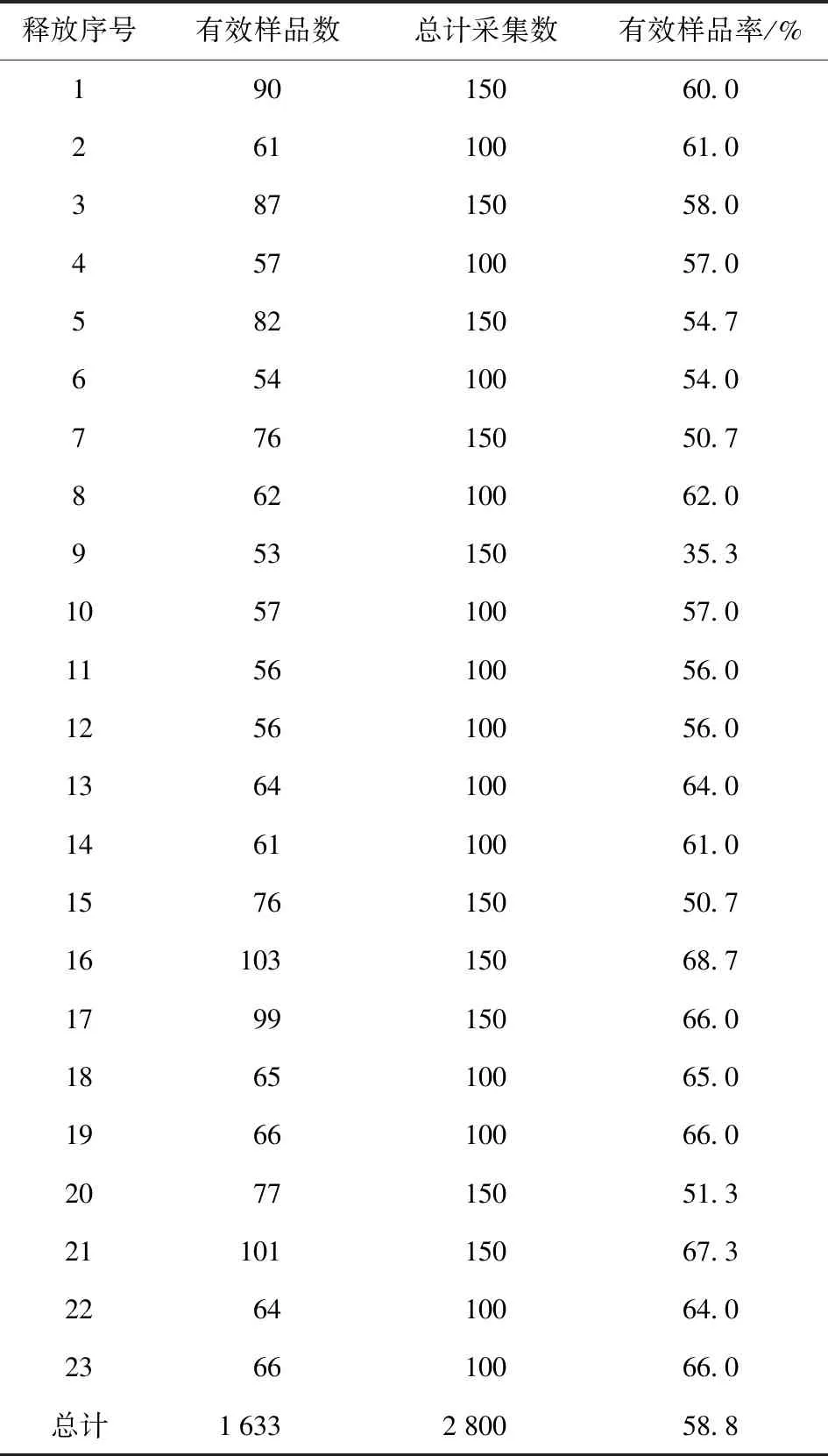
4.2 实验模拟与分析

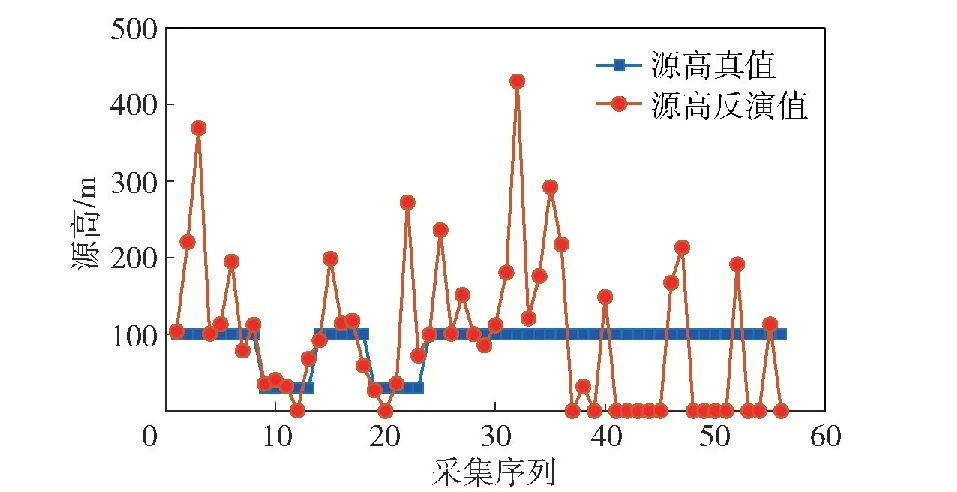
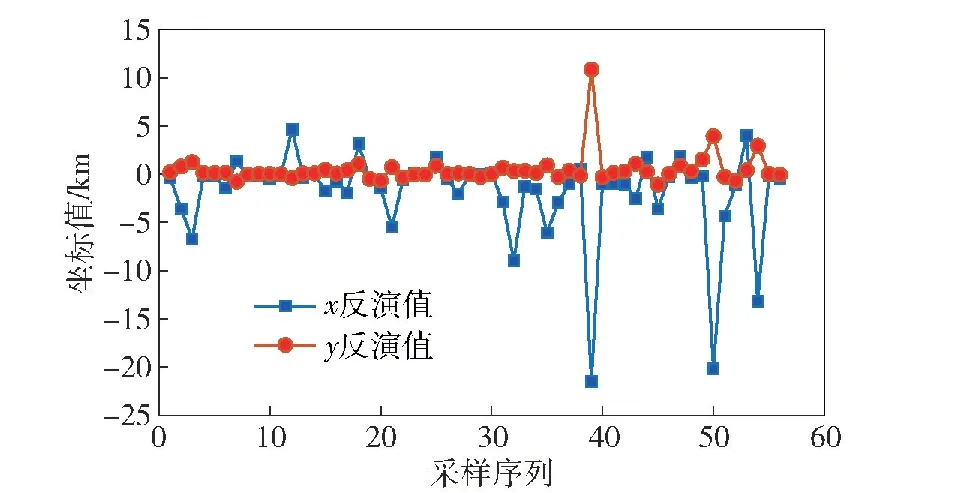
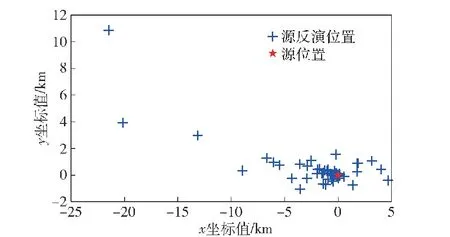
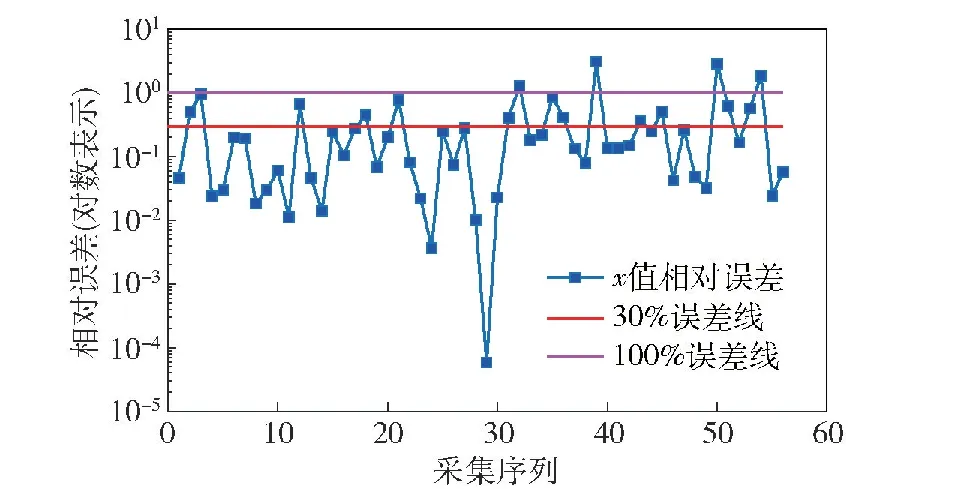

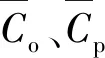
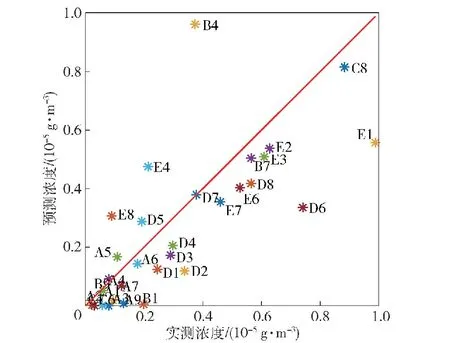

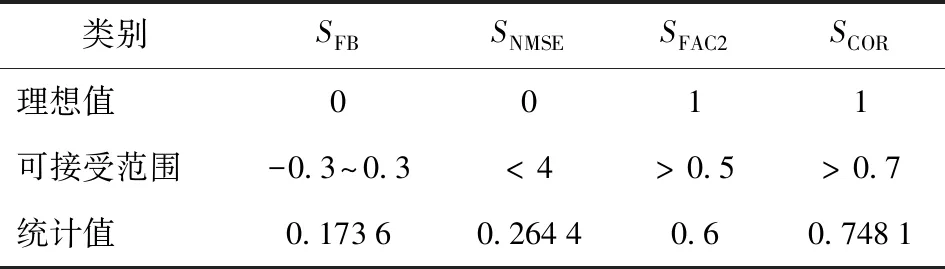
4.3 实验结果讨论
5 结论
