基于多项式流形内插的无线测向系统

李司, 刘寅生, 李旭, 杨明强

(1.北京交通大学 电子信息工程学院, 北京 100044; 2.公安部第一研究所, 北京 100048;3.北京交通大学 轨道交通控制与安全国家重点实验室, 北京 100044;4.北京交通大学 智慧高铁系统前沿科学中心, 北京 100044)

0 引言

电磁空间安全已经成为国家安全战略的关键环节,是国家整体安全体系的重要组成,其不仅关系到国防电磁权的争夺也关系到社会生活生产秩序的维护[1]。无线电监测是民用领域维护国家电磁空间安全的重要手段,而无线测向作为无线电监测设备的重要基础性功能,同时也是装备研制工作中重点的研究方向。

无线测向技术经过前期发展形成基本完备的理论体系,测向算法经历了传统测向算法向现代测向算法的发展历程[2]。传统无线测向算法依靠天线结构,通过接收信号的幅度与相位信息实现来波方向的估计[3-5],相关算法受到瑞丽限的制约,无法实现超分辨测向。目前无线电监测领域中设备大多仍然基于上述传统测向体制设计。随着基于阵列信号处理的波达方向(DOA)估计技术发展,多重信号分类(Multiple Signal Classification,MUSIC)算法[6]的提出对于无线测向领域具有重要意义,其不仅突破瑞丽限,实现超分辨测向,而且开创了子空间类现代测向算法理论。研究者基于该理论并结合不同应用场景,提出众多的改进算法[7-9]。超分辨测向技术为无线电监测设备的测向性能提升提供理论支撑。

面向工程应用的超分辨测向算法研究中,有效消除测向天线阵互耦影响是需要解决的重要问题之一。前期研究工作中抗互耦DOA估计算法可以分为互耦自校正法与互耦辅助校正法两类。互耦自校正法[10-12]的算法思想是采用互耦矩阵对阵列中天线单元间的互耦效应进行建模,而后采用联合估计算法同时对信号来波方向参数与未知的互耦矩阵进行估计。文献[10-11]基于均匀线阵与均匀圆阵天线阵列结构,提出了基于迭代估计的互耦自校正算法。文献[12]提出一种递归降秩算法,该算法采用递归处理结构实现了互耦矩阵与DOA联合估计,并解决了传统降秩算法[13]中的DOA估计模糊问题。文献[14]提出了非迭代自校正算法,基于广义奇异值分解,在互耦条件下得到DOA估计的解析表达。互耦辅助校正法包括辅助天线法与辅助信号法:其中辅助天线法[15]是依靠阵列特殊的结构,通过增加辅助天线阵元扩展天线阵列来对抗阵列互耦效应,从而可采用阵列中的子阵进行DOA估计,无需进行互耦校正;辅助信号法基本思想是将辅助信号源放置于一系列已知精确位置的方向格点,通过该已知方向信号源进行误差参数的离线估计,而后对误差加以校正[16-18]。

对比上述抗互耦DOA估计算法,自校正法其优点在于无需额外的辅助信号源与辅助天线,但缺点是复杂度高,特别是基于迭代的自校正算法,多维交替迭代运算量极大且收敛速度慢,全局收敛无理论保障;其次该类算法依赖于特殊的阵列结构(均匀线阵或均匀圆阵),制约其在一般性结构的阵列中应用。此外,辅助校准算法中辅助天线法也同样存在依赖特殊天线结构的问题。相比之下辅助校正法中的流形内插算法在处理复杂度和阵列结构适应性方面都具有较大优势,其将DOA估计中角度域搜索转换为流形样本的搜索,而流形样本中已经包含了互耦效应,因此无需进行互耦矩阵的估计。

本文针对现有抗互耦DOA估计算法不足并结合无线电监测设备研制需要,提出基于多项式流形内插的抗互耦DOA估计算法。该算法不仅保障工程应用中DOA估计算法的鲁棒性,并可实现小流行样本存储条件下高精度DOA估计。在理论分析与仿真的基础上,结合LTE下行信号搜索需求,提出了基于嵌入式处理器平台的原型测向系统设计,并给出实验测试结果。

1 互耦条件下基于流形内插的测向系统

1.1 系统模型

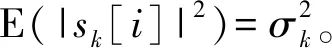
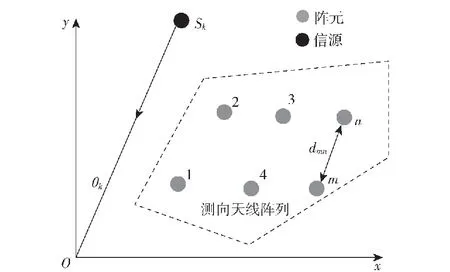
图1 天线阵列与信号示意图

根据上述模型描述,定义第m号天线阵元接收信号采样值为ym[i],则该阵列天线输出的接收信号采样向量为y[i]=(y1[i],y2[i],…,yM[i])T,且该向量可以表示为

(1)

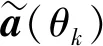
(2)

α为调节常数。

测向系统在获得阵列接收信号后,可由式(3)得到协方差矩阵:

R=E{y[i]yH[i]}

(3)

对协方差矩阵的特征值分解,可得

(4)

式中:Us为K个信号空间的特征向量;Un为M-K个噪声子空间的特征值向量。MUSIC算法正是基于上述子空间特性进行DOA估计的,实际测向系统中可由样值平均运算来估计协方差矩阵:

(5)

式中:N为样值平均运算的样点数。

1.2 现有线性内插的DOA估计算法回顾

在提出本文算法前,对现有线性内插算法进行简要回顾。如图2所示,基于线性内插的DOA估计算法基本思路为:在Q个已知方位角的方位格点位置θ(q)分别得到各流形向量样本(θ(q)),q=1,…,Q;随后利用MUSIC算法对离散方位格位置上的样本流形向量进行谱峰搜索,找到目标方位角所在的角度区间后,在角度域进行内插获得目标方位角的准确估计值。

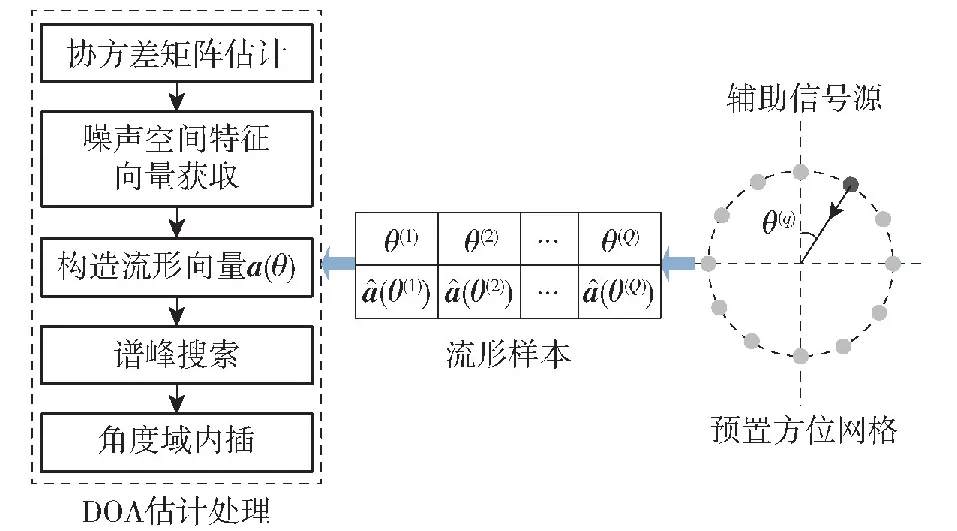
图2 基于线性内插的DOA估计算法

具体来说,基于线性内插的DOA估计算法处理过程[17]如下:

1) 在测向方位角区间均匀设置Q个离散方位格点,各点方位角记为θ(q)(1≤q≤Q),将辅助信号源s[i]依次放置于各方位格点,假设辅助信号源具有归一化发射功率,即E(|s[i]|2)=1。当信号源放置于θ(q)方位格点时,由式(1)可得阵列的输出向量为

(6)

利用式(7)可以获得θ(q)方向的流形样本:

(θ(q))=E(s*[i]y[i])

(7)

式中:s*[i]为s[i]的共轭。

工程实现中可采用样值平均替代式(7)的统计平均,依次获得各预置方位格角度的流形样本并存储于测向设备中。

2)在获得各预置方位格点的流形样本向量后,通过式(8)进行DOA估计角度区间的粗搜:

(8)

3)在获得粗搜角度区间后,进一步通过相邻预置方位格角的线性组合得到DOA精确估计:

=c0θ(q)+c1θ(q+1)

(9)

式中:c0和c1为线性组合系数,系数可由如下关系式进行求解:

(10)

c0+c1=1。

分析上述算法过程不难发现,现有算法将方向角度搜索转换为流形向量样本搜索,由于流形向量样本中已经包含了互耦因素信息,因此该转换使算法具有抗互耦效应的特性,且最终可由相邻方向格角度的线性组合得到精确的DOA估计。但通过分析也可发现,由于该算法的内插操作是在角度域进行的,因此其估计精度完全取决于预置方位格的密度。当系统预期估计精度较高时,为获得密集部署的预置方位格点的流形向量样本,需要大量预处理工作,同时大量的流形向量样本对测向设备存储空间也造成较大负担。

2 基于多项式流形内插的DOA估计算法

针对现有算法在高精度DOA估计中预处理及存储负荷高的问题,本文提出基于多项式流形内插的DOA估计算法。与1.2节中回顾的线性内插不同,1.2节中的线性内插是在角度域进行的,而本文所提出的内插方法是针对流形向量进行的。本文算法通过对流形向量的多项式内插实现搜索流形向量的构建,在有效对抗天线阵互耦效应的同时实现小流行样本下高精度DOA估计。

2.1 算法步骤

基于多项式流形内插的DOA估计算法处理可以分为如下3个步骤:

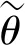
2)流行向量内插。根据步骤1中方位角区间粗搜结果,利用θ(q)周围P个预置方位格点的流形向量样本,基于P阶多项式流形内插构造搜索流形向量。P阶多项式流形内插表达式如下:

(11)

式(11)中多项式系数可由拉格朗日插值公式得到:

(12)

3)方位角精细估计。在完成搜索流形向量内插构造后,利用式(11)中获得的内插流形向量,可在[θ(q),θ(q+1)]角度区间内通过式(13)遍历搜索,进一步完成精细方位角估计:

(13)

相比于标准的MUSIC算法处理,式(13)虽然缩小了谱峰搜索的范围,但遍历搜索处理仍然存在较大的运算负荷。针对这一问题,本文进一步提出低复杂度的求解方法。该方法继续在[θ(q),θ(q+1)]区间内设置R个精细方位格点,由式(14)替代式(13)进行方位角所在精细区间的估计:

(14)

式中:θ(q,r)为各精细方位格点方向角。

2.2 算法分析

下面就本文提出的基于多项式流形内插的DOA估计算法中内插阶数对估计值求解方法影响以及算法同频多信号测向能力两方面进行深入分析。

2.2.1 内插阶数对算法影响

对于多项式流形内插DOA估计算法,其核心是利用MUSIC算法中子空间正交关系:

(15)

进行DOA估计处理,而具体DOA估计求解方法与构造内插流形向量(θ)的阶数是相关的。

当内插阶数P=2时,在基于多项式内插生成(θ)的处理中仅有两个样本流形向量参与内插运算,由此多项式内插退化为线性内插,根据式(11)和式(12)可得(θ)的生成表达式:

(θ)=c0(θ(q))+c1(θ(q+1))

(16)

(17)

(18)

将式(16)代入式(15)可以验证:在c0+c1=1约束条件下,式(17)与式(18)中的c0与c1是式(10)的解。因此,在P=2时,多项式内插退化为线性内插,可得到与文献[17]中相同的DOA估计解析表达式:

=

(19)

当内插阶数P>2时,在基于多项式内插生成(θ)的处理中有更多的流形向量样本参与高阶内插运算,将式(11)代入式(15),可得

(20)

式(20)中对于未知变量θ具有非线性的表达形式,难以推出DOA估计的解析表达。因此,在P>2条件下,对多项式流形内插的DOA估计求解处理较为直接的方法是采用MUSIC算法思想,在[θ(q),θ(q+1)]区间方位角进行谱峰搜索,但该搜索处理势必造成较高的运算复杂度。相比之下,本文提出的低复杂度算法,其以不同的方位格区间精度逐次逼近搜索,最终可将多项式内插降为线性内插,从而避免高复杂度的角度域遍历搜索处理。

2.2.2 同频多信号测向能力

如图3所示,对于本文提出算法而言,空间中同频多信号按照方向角间隔不同,可能存在两种分布情况:1)同频多信号的来波方向角间距大于预置方位格角度;2)同频多信号的来波方向角间距小于预置方位格角度。

图3 同频多信号空间谱

图3(a)表示为同频多信号来波方向角间隔大于预置方位格角度的情况。在该分布情况下,本文提出算法可以由方位角区间粗搜步骤得到各信号所处区间,而后在对应区间内进行流形向量内插得到搜索流形向量,最终由方位角精细估计得到各信号来波方向。此外,1.2节中回顾的现有算法也可实现该情况下的同频多信号测向处理。

图3(b)表示同频信号来波方向角间隔小于预置方位格角度的情况。在该分布情况下,本文提出算法可以在得到多信号所处的粗搜区间后,继续在该区间内通过内插流形向量进行搜索,最终得出多信号的精细角度方向。而且,当多信号落入不同的精细区间时,还可采用式(14)给出的低复杂度算法进行各方位角估计。相比之下,1.2节回顾的现有算法仅基于方位格点样本向量进行方位粗搜,而后直接由两相邻方位格样本向量进行DOA估计求解,因此其不具备图3(b)所示的方向间距较小情况下的同频多信号测向能力。

通过对本算法同频多信号测向能力分析,可进一步表明基于多项式流形内插的DOA估计算法在相同样本流形向量条件下,较现有算法具有更高的测向精度。

3 算法仿真

为验证算法不受阵列结构限制,仿真环境中测向阵列选择V形阵列结构[20],阵元数为7,阵元间距为目标信号的半波长,该阵列结构具有全向测向能力。空间来波信号数量K=2,两信号在方位角[0°,360°]区间随机产生。Q个预置方位格点均匀分布在[0°,360°]区上,预设方位格的角度间距为360°/Q,多项式内插中精细方位格点数R=15。阵列的互耦矩阵C(θk)由式(2)定义生成,调节常数α系统随机产生。此外,仿真中进行协方差估计运算的快拍数N=500。

图4给出了相同预置流形样本下,不同内插阶数条件下DOA估计性能对比结果。仿真中选择Q=36,即预置方位格点方向间距10°。由性能对比可见,在高信噪比区间较高的内插阶数可取得更优的DOA估计精度,而在低信噪比区间内插阶数的提高对于DOA估计的性能提升不明显。在实际系统设计中可通过监测目标信号信噪比参数动态调整内插阶数。

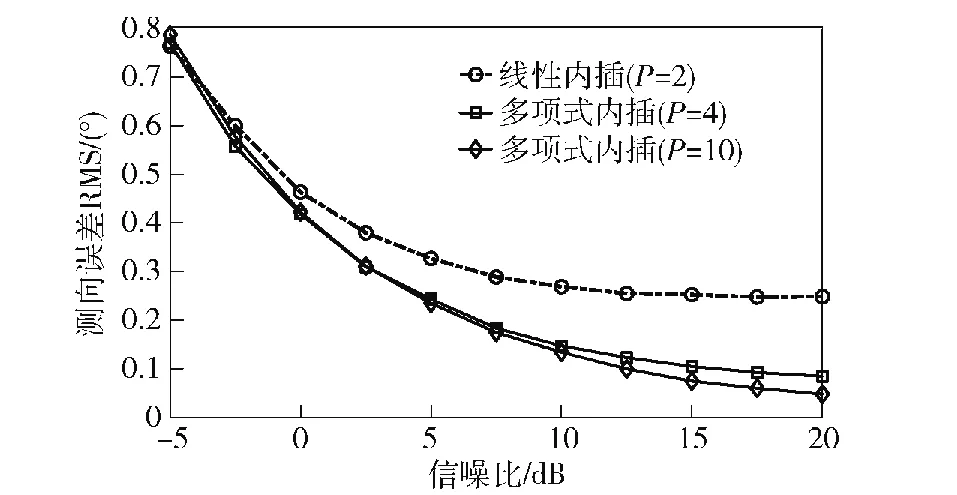
图4 不同内插阶数下DOA估计性能

图5给出了线性内插DOA估计与多项式流形内插DOA估计算法的性能比较。多项式流形内插选择预置方向格角度间隔为10°,线性内插分别选择预置方向格角度间隔1°和6°。通过性能曲线对比可知,在间隔10°的条件下多项式流形内插DOA估计算法性能与间隔1°的线性内插算法性能相近,并明显优于间隔6°条件下线性内插算法性能。由此可见,在高阶内插条件下,基于多项式流形内插算法的小流形样本高精度DOA估计性能优势较为明显。

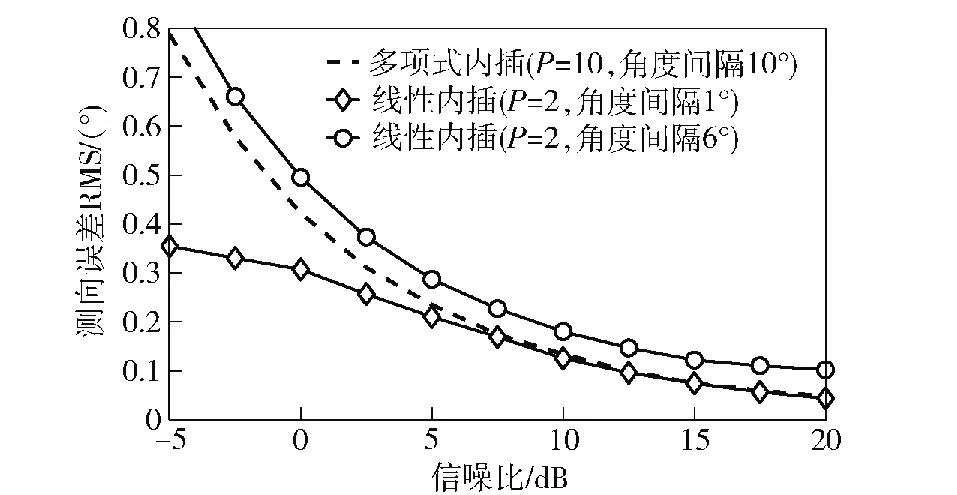
图5 线性内插与多项式流形内插的DOA估计性能比较

此外,通过上述仿真实验可验证基于流形内插的DOA估计算法可有效对抗阵列互耦效应,且算法不受阵列结构的约束。

4 抗互耦无线测向系统

4.1 测向机原型系统设计

针对LTE移动通信系统下行信号实时测向需要,采用多项式流形内插DOA估计算法,实现无线测向原型系统设计。该设计方案未来可用于“伪基站”搜索设备的研制工作。系统设计中关键单元包括:测向阵列与基于嵌入式处理器的多通道测向接收机。

4.1.1 测向阵列

原型系统的测向阵列为8个低剖面天线阵元构成的均匀线阵,阵列中阵元采用偶极子结构设计,偶极子天线外形为11.5 mm×11.5 mm,支持频段 1 710～2 650 MHz,增益为9.5 dB,均匀线阵阵元间距11.5 mm,设计测向角度范围-30°～30°。阵列天线高度30 mm。该天线阵列中阵元排列紧密,便于与测向机单元共同集成于紧凑的设备结构中,满足不同机动平台的搭载要求,但天线阵元密集排布以及未来设备内部散射部件势必产生互耦效应,影响DOA估计算法的可靠性。

4.1.2 基于嵌入式处理器的多通道测向接收机

系统中测向接收机采用美国Xilinx公司生产的ZYNQ系列全可编程处理器与美国ADI公司生产的无线收发处理器AD9361实现核心测向卡设计,每个测向卡以单板双AD9361配置进行设计,支持4通道接收,接收频段覆盖70 MHz～6 GHz,并针对移动通信频段设计有相应频段的带通滤波器,通过开关矩阵进行滤波通道选择。测向卡接收通道动态范围60 dB,增益按1 dB步进可配置,通道接收灵敏度-105 dBm,同时射频前端设计有通道校准电路。针对大规模多通道测向接收机需要,测向卡支持多卡级联扩展,满足不同规模阵列下测向系统设计需要。

图6所示的原型系统采用主从双卡模式构建8通道测向接收机。系统中主测向卡实现自身多通道信号接收、全部通道基带采样数据汇聚,以及校准与测向运算处理;从测向卡则在主测向卡的控制下实现多通道信号接收处理,并将自身多通道基带采样数据通过以太网口传输至主测向卡。此外,原型系统设计有上位机软件,该软件以IP地址区分各测向卡,实现多测向卡设备管理与测向结果的实时展示。

图6 无线测向原型系统

多通道数字测向机要求硬件保证各通道基带采样同步以及通道间相位相干。为保障上述特性,测向卡设计有级联扩展所需硬件接口。如图6所示连接,主测向卡对从测向卡提供基带处理时钟,保证两卡基带时钟同步,同时主测向卡处理器通过同步控制信号对两卡中4个AD9361芯片进行功能配置,从而实现主从两测向卡上8个通道基带采样时钟的相位对齐。此外,主从测向卡均以信号源输出作为射频本振,从而保证8通道接收的相位相干。

在满足基带采样同步与接收相位相干条件基础上,测向机还需要校准处理去除接收通道残留的固有相位偏差。本文系统设计中,主测向卡处理器通过同步控制信号控制全部射频前端的校准电路,并以主测向卡中通道1为参考实现各通道残留相位偏差估计。每次测向任务启动前,主处理器均需要启动校准流程以去除当前通道残留偏差。经校准处理后,各通道间相位误差可控制在0.5°以内。

4.2 基于嵌入式处理器的算法实现

本文提出的抗互耦DOA估计算法基于ZYNQ系列的XC7Z020型号处理器实现,该SoC处理器将ARM处理器(PS)与FPGA器件(PL)在单芯片内部组合,具有较强的并行处理能力。SoC处理器的PS部分包括双核Cortex-A9处理器和NEON协处理器,为完全发挥处理器能力,设计中在双核ARM处理器上采用嵌入式Linux操作系统;SoC处理器的PL部分由Artix-7等效可编程逻辑单元构成,其包含丰富的逻辑处理资源、DSP处理资源,以及存储资源。

测向系统软件功能框架如图7所示,算法软件实现分为PS与PL两部分,其中PS部分为主处理器完成多通道数据汇聚与DOA估计算法处理,PL部分为协处理器实现射频通道信号的实时采集。PS与PL部分层间采用APB接口实现功能寄存器配置查询以及流形样本数据读取等低速数据交互,采用AXI-HP接口实现高速率的通道采样数据交互。

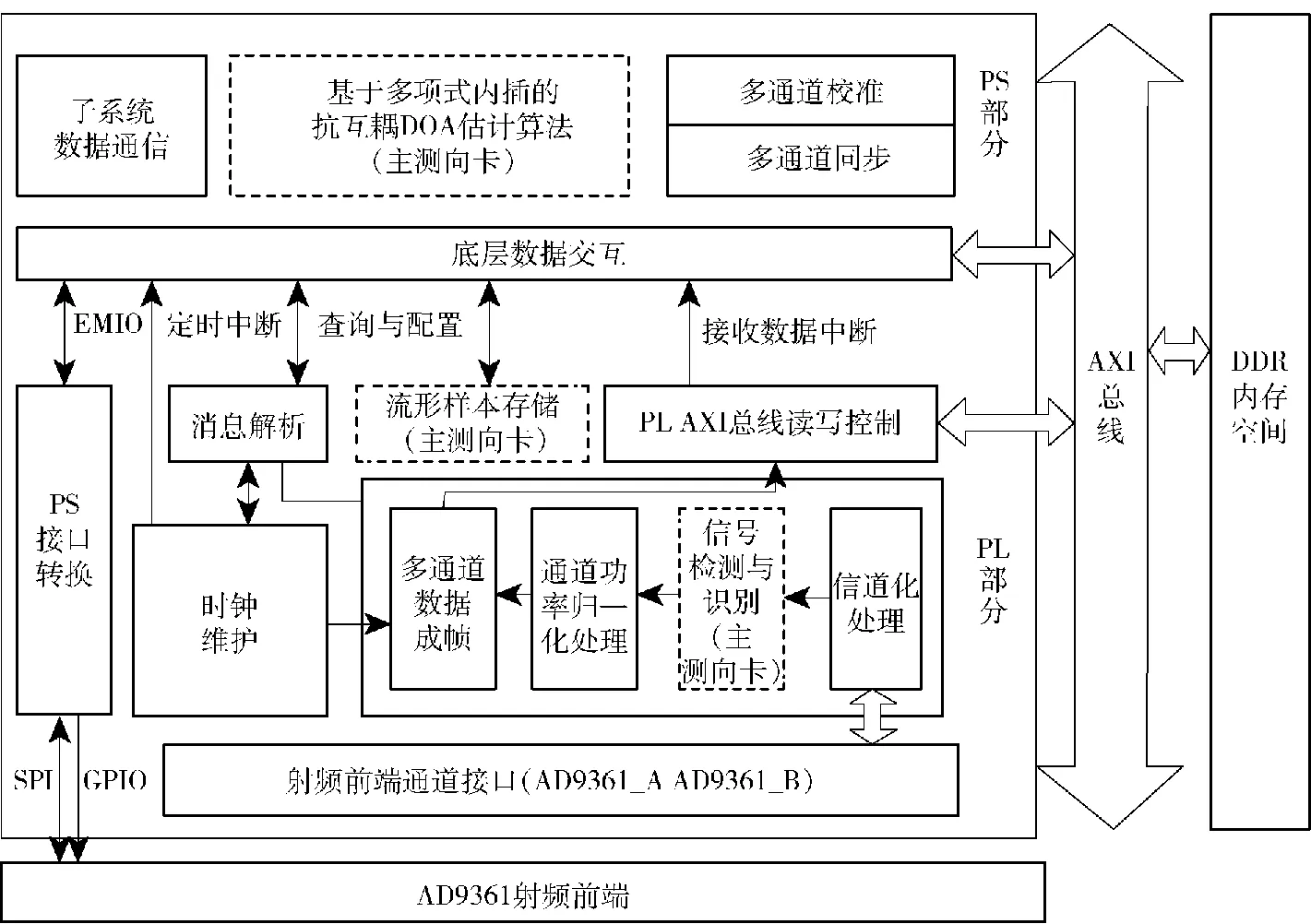
图7 软件设计功能框图

4.2.1 PS部分软件实现

PS作为主处理器负责系统整体工作流程调度,与其测向卡及上位机间的数据交互。具体软件设计流程如下:系统上电后PS响应上位机软件参数配置,配置成功后主测向卡控制从卡完成多通道的同步与校准,完成校准后主测向卡PS启动测向处理。测向处理中主处理器根据各通道接收数据帧结构中的时间戳信息完成数据汇聚,而后按照本文提出的抗互耦DOA估计算法进行处理,算法实现过程如图8所示。算法中预置方向格点的角度间隔为10°,根据测向系统的设计目标,系统预存有2 330 MHz、2 349.8 MHz 以及2 585 MHz 3个频率下,每个频率对应7个方位格点的流形向量样本,算法处理中内插阶数为4,协方差矩阵估计快拍数为500。

输入:测向阵列接收信号y[i],测向目标数K=1

快拍数N=500,精细方向格数R=10

2:特征值分解,得出噪声子空间特征向量Un

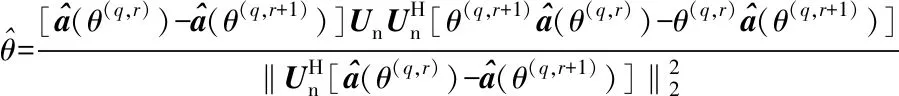
图8 基于多项式流形内插DOA估计算法

原型系统可实现特定LTE小区下行信号检测,并从目标LTE小区下行同步时隙提取窄带测向信号,且系统设计测向结果更新时间为0.5 s。测向卡ARM处理器主频为866 MHz,算法可在更新时间内完成测向结果的输出,满足系统实时性要求。

4.2.2 PL部分软件实现

PL作为从处理器在PS调度下实现天线通道数据的实时同步采集与成帧处理。数据处理流程如下:射频前端接口完成多通道AD9361的复基带信号接收,而后对接收信号进行滤波降采样等信道化处理;得到待测频带数据后进行功率归一化,防止实际工程部署中部分天线受到突发近场遮挡引起接收功率波动;归一化处理后多通道数据进行数据成帧处理并加注时间戳信息;成帧后数据经过AXI总线写入DDR外部存储空间,并向PS发送接收数据中断信号。PL中设计有时钟维护模块由该模块为多通道数据帧提供时钟定时信息。

在主测向卡中设计有针对LTE物理层信号体制的检测与识别模块,并可以根据LTE物理层帧结构实时提取所需时频位置的采样信号,从而实现对不同信号目标的测向处理。此外,流形向量样本数据存储于主测向卡的ROM中。主测向卡中PL部分资源占用情况如表1所示。

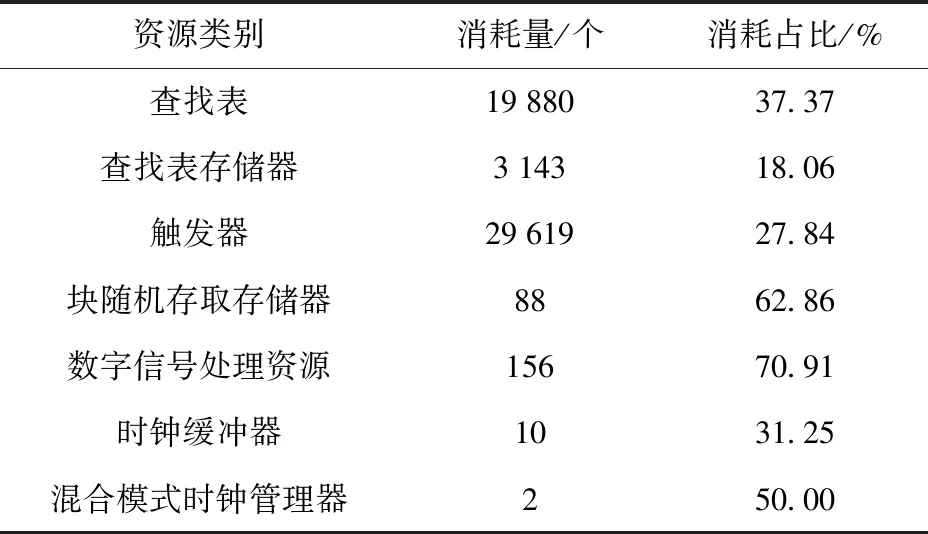
表1 PL资源占用

4.3 实验验证

为验证原型系统的性能,在微波暗室环境下对系统进行测试。测试中阵列天线固定于数控转台,并可由转台调整其方向,从而等效为目标信号处于不同的来波方向。目标信号由信号源E8267D产生,并由暗室中喇叭天线进行发射。测试前通过控制转台旋转,由式(7)获得方位格点的流形向量样本,并存入主测向卡中。

测试过程中选择法线两侧各3个来波方向进行测试,且所选测试方向均非预设方位格位置。测试目标信号为LTE模拟小区的下行信号,信号源发射功率设置为-30 dBm,并分别在2 330 MHz、2 349.8 MHz、2 585 MHz三个典型LTE载波频率下对原型系统的性能进行测试。

测试结果由表2给出:测试中在各载波频率下对不同来波角度方向分别进行120次测量,并将结果进行均方根误差统计,测试表明各频段下原型系统可实现误差为1°以内的测向。

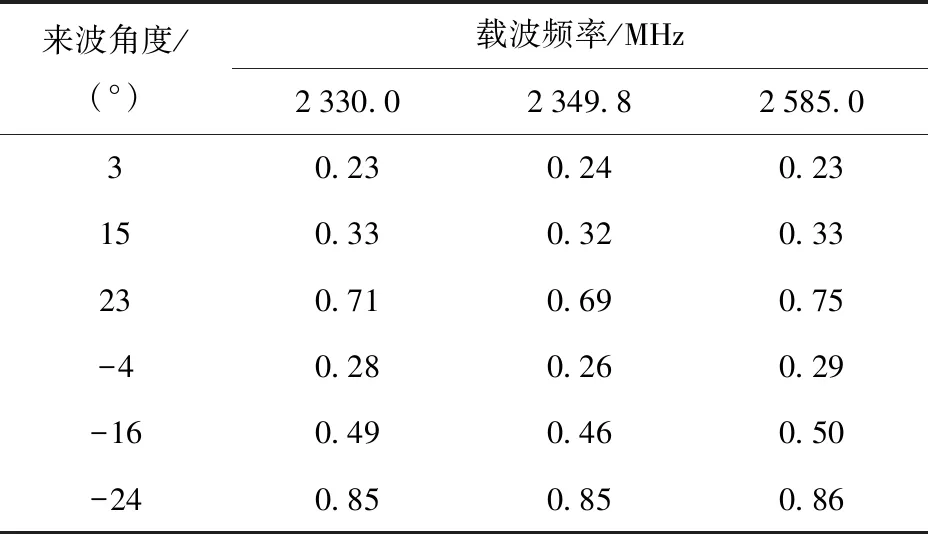
表2 测向结果均方根误差

5 结论

本文提出基于多项式流形内插的抗互耦DOA估计算法,并基于嵌入式处理器对算法进行硬件验证。该算法采用多项式流形内插实现小预存流形向量样本条件下高精度测向,有效降低了流形内插类方法在预处理以及样本数据存储环节对测向设备的负荷。此外该算法采用逐次逼近思想,以精细角度区间搜索代替角度遍历搜索,有效减少搜索运算的负荷,从而提升了算法的实时处理能力。在理论分析与仿真验证基础上,基于嵌入式处理器完成算法的实现。系统设计采用主从双卡模式构建8通道测向系统原型,并基于8阵元线阵在微波暗室中完成了系统性能的测试。测试结果表明,该原型系统可实现针对LTE下行信号的高精度实时测向。