一种单级控制的高精度指向系统研究

杜永刚, 王雪松, 王禺林

(中国空间技术研究院 兰州空间技术物理研究所, 甘肃 兰州 730000)

0 引言

高精度指向系统被广泛应用在航天、航空领域,是该领域内的关键技术。在航天、航空领域,各种光学系统对其指向提出了极高的要求,如美国的詹姆斯·韦伯望远镜要求其指向系统的精度达到0.007″[1],美国论证中的大型紫外-可见光-红外综合天文望远镜要求其指向系统的精度不低于0.000 34″[2]。近期中国研制的小卫星“凝视”热成像仪以及中国首颗太阳专用观测卫星的X射线成像仪都对其指向系统的精度提出了极高的要求[3-4],中国的“墨子”号量子卫星的指向系统的精度达到0.000 4″[5]。光电跟瞄设备是航空战斗机吊舱系统的核心组成,其指向系统的精度达到了亚微弧度的精度,如某机载激光通讯吊舱采用了一种复合指向系统,其指向精度可达0.002″[6],高精度指向系统也是航母舰载机着舰引导光电设备的关键组成[7]。

近年来光通讯技术发展迅猛,该领域也对高精度指向技术表现出强烈的需求态势,如现代民用无人机的集群控制采用了激光通讯,它的核心组成之一就是高精度指向系统[8],它也是水下激光通信系统的核心组成[9]。高精度指向系统的研究依然具有重要的意义和价值。

目前,采用压电陶瓷致动器的指向系统可以实现单级控制的高精度指向的性能[10-12],但是这种指向系统的工作空间极小[13-14],限制了其应用,所以现在的高精度指向系统采用了双级控制技术,即采用一级机构稳定加上快速反射镜二级稳定的粗精双稳定系统,这种双级系统具有较高的技术复杂性,因此单级控制的高精度指向系统受到了广泛关注。李仕华等[15]优化了一种球面5R指向机构,提高了其工作空间和灵巧性。田少乾[16]提出一种新型的3-RRCPR并联指向机构,通过改进控制算法使其角位移误差小于0.85°,其线位移误差范围是0.02～0.03 mm。白智龙等[17]提出一种单级串联指向机构,其指向机构是万向节结构,通过研究永磁同步电机的控制算法,使该指向系统的稳态指向精度达到了1″。王玫羽等[18]提出了一种新型串联球面指向机构,其应用对象是机载光电平台,实现载荷在俯仰、方位及横滚的三轴调整,其测试的指向误差不大于0.25°。殷康程等[19]研究了一种星载双反射天线的指向机构,该指向机构将双轴间的连杆作为支撑和运动传递组件,具有运动范围广、结构紧凑、体积小、重量轻等特点,其双轴的工作空间分别为0～163°和0～360°,其指向精度优于0.03°。赵颖等[20]研究了一种卫星天线的指向机构,这种指向机构是电机驱动的一个单自由度关节,其单轴精度可以达到0.008°。杨鹏等[21]则报道了一种应用于空间光学跟踪系统的高精度二维指向机构,它承受的光学载荷质量约为100 kg,指向精度优于0.014°。

随着空天地海一体化的军事发展技术需求,空间立体化作战系统对其天地通讯技术提出了更高的要求,要求某指向系统具有小体积、大承载以及高精度的性能指标,同时要求低成本,因此不能采用复杂和高成本的双级控制指向系统,在这种背景下,本文提出一种单级控制的高精度指向系统,并通过理论计算和实验验证的方法对其进行了研究,详细阐述了这种单级控制的高精度指向系统的工作原理、理论模型、模拟仿真与实验测试,研究成果为后续工程应用奠定了基础。

1 指向系统组成及原理

1.1 组成

图1为这种单级控制的高精度指向系统的组成,其主要构成为传动机构、控制器以及上位计算机。该指向系统通过消除传动环节的位置浮动实现高指向精度的性能,其技术指标是:单轴误差不大于0.005°,空间合成误差不大于0.008°,载荷不小于100 kg。

图1 高精度指向系统的组成结构

考虑到工程应用,该指向系统采用了嵌入式控制技术,控制器的软件由C语言编写,指向指令由一台上位计算机模拟并给出。上位计算机为下位控制器给出指向命令,下位控制器按照指令解算出执行机构的执行参数,即两个分支的输出位移,而位置传感器则把指向位置反馈给控制器,根据误差消除算法,控制器会对实际的指向位置进行修正直至达到目标精度。

1.2 传动及控制原理

图2 并联机构的组成

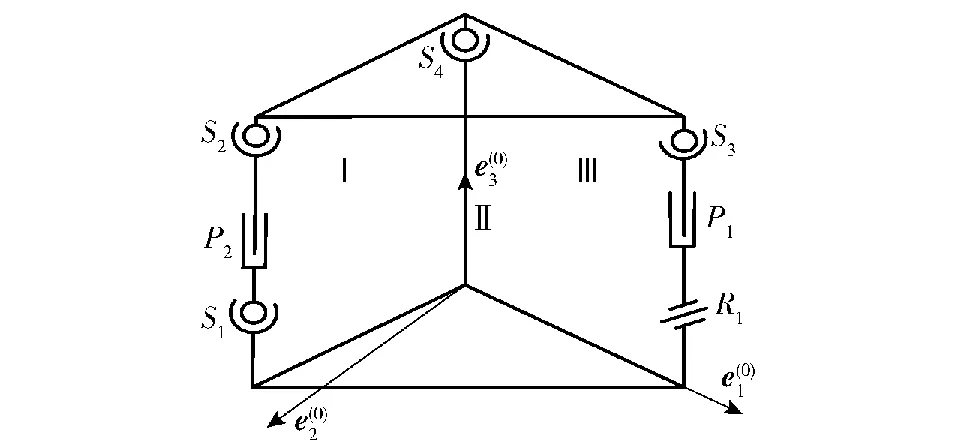
图3 机构原理图

对于空间机构的自由度计算方法已提出多种观点,普遍认可的方法是转换空间机构为平面内的解算关系[23-24]。式(1)被用来计算这种并联机构的自由度:

W=Px-λ-3N

(1)

式中:W是空间机构的自由度数目;Px是空间机构运动副的自由度总数;λ是空间机构运动副的多余自由度数目;N是空间机构的封闭环数。本文设计的指向机构有3个封闭环,分别是环Ⅰ、Ⅱ、Ⅲ,封闭环的位置见图3。对于环Ⅰ,其自由度为WⅠ=10-6-3×1=1;对于环Ⅱ,其自由度数WⅡ=12-8-3×1=1;对于环Ⅲ,其自由度数为WⅢ=8-5-3×1=0。因此整个指向机构的自由度数为W=WⅠ+WⅡ+WⅢ=2,表明指向机构的自由度符合了设计。

综合误差是导致并联机构精度损失的主要原因[25-26],设计合理的控制策略可有效降低并联机构的精度损失。基于RPS-SPS并联机构,本文开发了误差消除算法,形成以消除误差为核心目标的控制策略,该控制策略如图4所示。上位计算机给出预期指向矢量nexp,该指向矢量由一个控制器完成解算,控制器解算后得到两个分支的矢量值pexp,控制器根据该值调整两个分支,一个超高精度的位置传感器测量实际位置,并被表示为矢量ntrue,指向误差是矢量ntrue和nexp之间的差异,并被定义为μerror=‖ntrue-nexp‖。如指向误差大于0.005°,控制器继续调整机构,当指向误差小于0.005°,指向机构则停止调整,过程调整量由误差消除算法解算并给出。

图4 指向机构的控制策略

铰链间隙会导致传动误差[27-28],本文利用一种新型滚动球轴承消除球铰的配合间隙误差。这种轴承通过滚子的过盈配合消除了运动间隙,同时该球轴承的结构进一步简化了误差消除算法。图5是这种滚动球轴承的外形。

图5 指向机构的滚动球轴承

本文提出一种双模型比较的误差消除算法,其原理是建立一个标准模型,该标准模型作为标准对机构实际输出位置进行误差校验。设定控制误差带为μerror≤0.005°,算法根据双模型的误差校验数据计算出指向的调整量,控制器再根据调整量调整指向机构的分支矢量pcor,当指向误差小于控制误差带后,指向机构停止位置指向,图6为这种误差消除算法的流程,流程图说明运动学模型是由反向解算模型和正向解算模型组成。

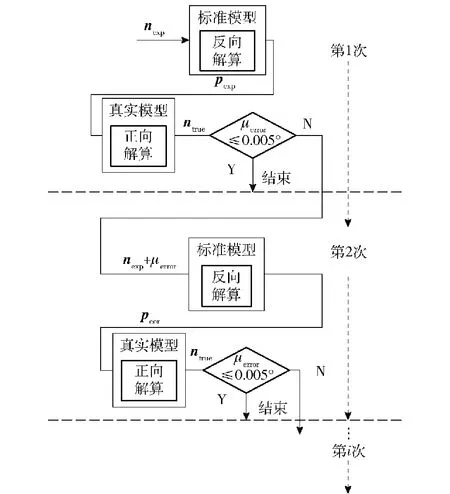
图6 指向机构的误差消除算法流程

2 运动学模型及其仿真计算

2.1 运动学反解模型

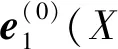
图7 空间坐标系的定义

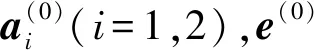
图8 单分支的矢量定义

根据空间几何学和单分支的矢量定义,可得

(2)

(3)

(4)

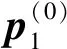
(5)

(6)

(7)

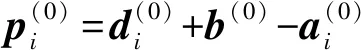
2.2 运动学正解模型

正向解算模型是从两个分支矢量pi推出指向矢量n。图9为两个分支矢量的定义,定义从球铰S3指向球铰S2的矢量为f,其他矢量的定义同图8。

图9 双分支的矢量定义

(8)

(9)

2.3 仿真计算

本文利用MATLAB软件编写上述模型的仿真程序,表1中列出了指向机构的参数。因参数b的精度难以保证,计算程序设定b的误差范围为5 mm,然后对这种跟踪指向系统的工作空间和指向误差等进行仿真计算。

表1 指向机构的参数

图10为指向机构工作位置空间的计算结果。图10中坐标轴是指向矢量n绕X、Y轴的工作角,云图则表达了指向矢量n和Z轴夹角,从图10中可得出该指向机构的工作空间为X、Y两轴±9°。

图10 机构工作空间的仿真结果

指向误差的仿真结果如图11和图12所示。图11 中的数据表明该指向机构的理论单轴误差不大于0.001 2°,图12中可以得出其理论空间合成误差不大于0.002°。

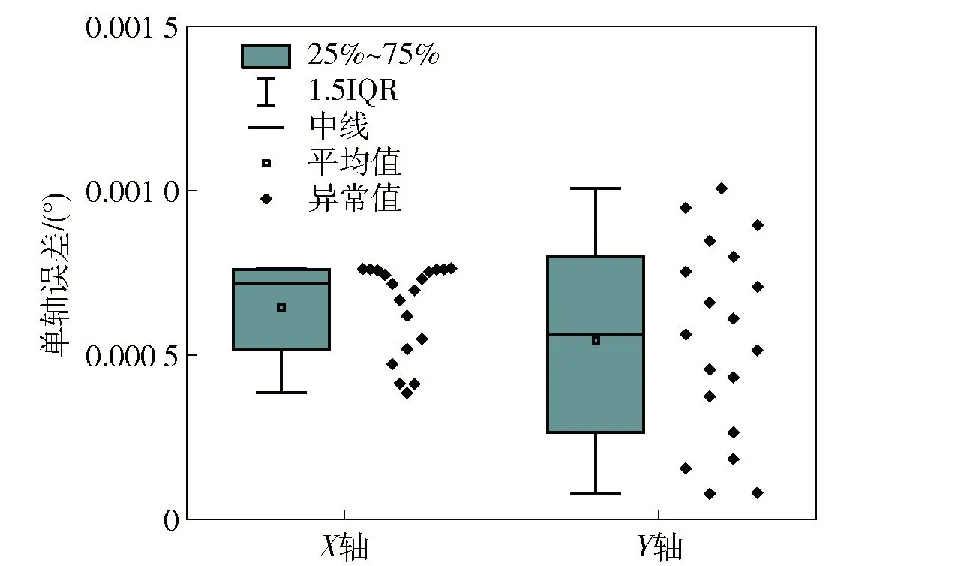
图11 单轴误差的仿真结果

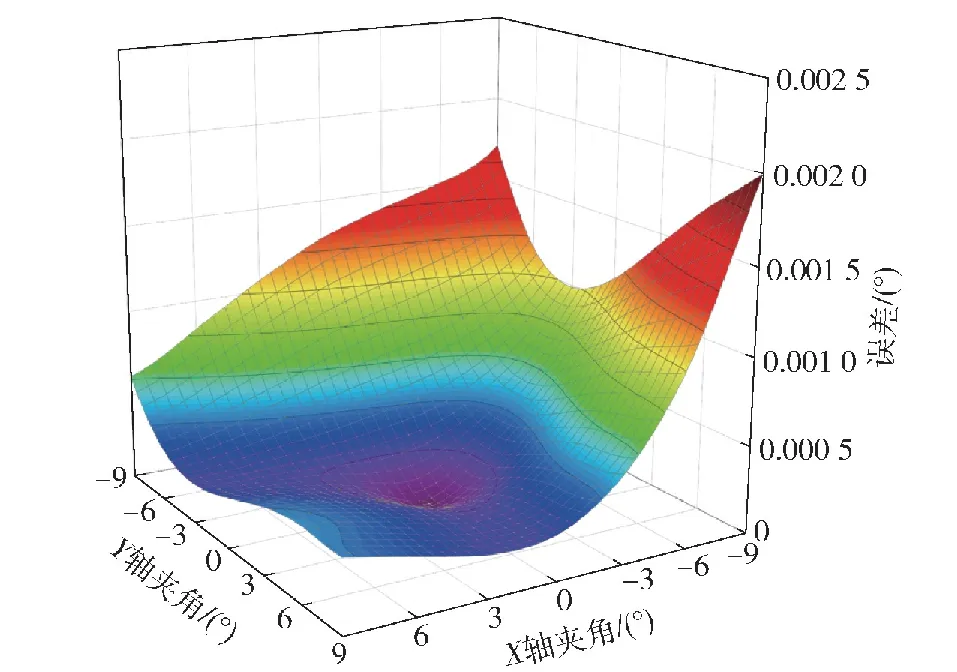
图12 合成指向误差的仿真结果

3 实验及分析

3.1 实验

本文开发的原型机如图13所示,并开展了实验测试研究。原型机的参数选用表1中的数据。

图13 系统原型机的外观照片

首先测试了指向系统的工作空间。上位计算机给出两轴每间隔3°的指向指令,位置传感器获得指向机构两轴的角度位置数据,图14为测试数据形成的位置点图,从中可以得出该系统的工作空间满足了两轴±9°的要求。

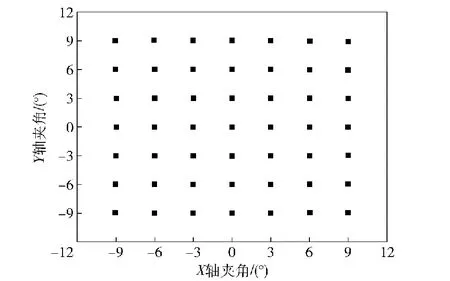
图14 工作空间的测试结果

其次,分别测试了空载和110 kg载荷下的单轴指向误差,测试的结果如图15所示,从中可以得出在两种载荷条件下该系统的单轴指向误差均不大于0.004°。同时,测试了指向系统的空间合成指向误差,其测试结果如图16所示,从中可知在两种载荷条件下,该系统的空间合成指向误差均不超过0.006°。

在研究新型城镇化背景下我国城市精明增长与蔓延发展的关系时，不可割裂看待精明增长与城市蔓延，这两者是城市发展过程中不可或缺的阶段，有相互交织、相互依存的关系，对各地城市发展都有一定的意义。

图15 单轴误差的测试结果

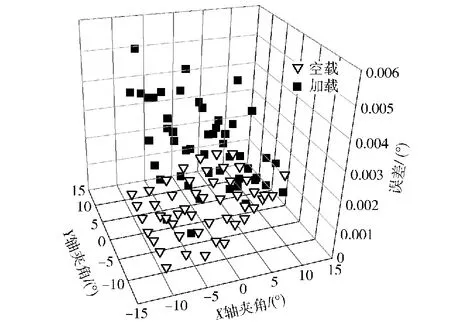
图16 合成误差的测试结果

然后,本文中也验证了双模型比较误差消除算法的有效性。设置指向误差控制带为0.005°,测试了X、Y两轴分别间隔1°的位置比较次数,其测试的数据如图17所示。测试结果表明:在两种载荷条件下,误差消除算法的比较次数均不超过3次。

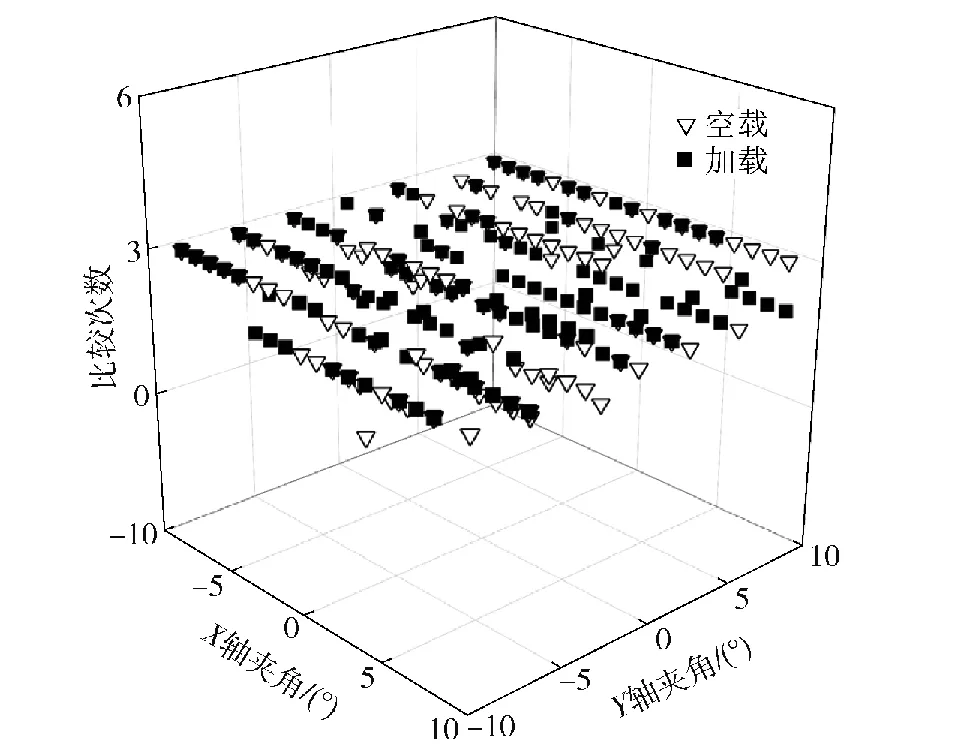
图17 比较次数的测试结果

最后,开展了指向系统的响应速度测试。响应速度是评价指向系统的重要指标,本文用指向稳定时间表征高精度指向系统的响应速度,指向系统的稳定时间越短,表示其响应速度越高。设定控制误差带为0.005°,并测试了原型机的指向稳定时间,图18为测试的结果。实验数据表明在两轴±9°的工作空间内,原型机的指向稳定时间均小于100 ms。

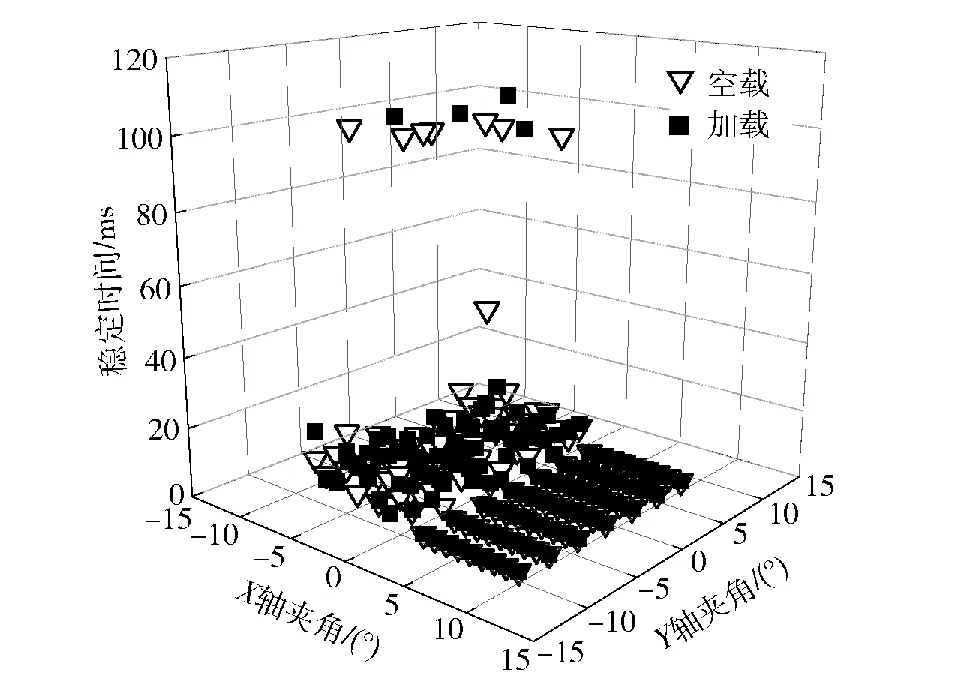
图18 稳定时间的测试结果

3.2 结果分析

本文旨在获得一种单级控制的高精度指向系统,要求其建造成本低,同时具有小体积、大承载以及高精度的性能指标。两个关键设计使本研究达到了预期目标,其一是该指向系统采用了一种2自由度的RPS-SRS并联机构,这种新型的并联机构利用中间球铰副消除了位置浮动,同时也消除了载荷重量对传动链的作用;其二是采用了基于RPS-SRS并联机构的双模型比较误差消除算法,算法进一步改善了指向精度和稳定性。理论模型的仿真结果表明这种指向系统的工作空间可达到两轴±9°,其单轴误差不大于0.001 2°,其合成误差不大于0.002°。

为进一步证实这种设计思想的正确性,本文开展了原型机的实验研究,原型机采用和理论模型相同的机构参数,其测试结果证明指向系统的工作空间可达两轴±9°,单轴误差不大于0.004°,其空间合成误差不大于0.006°,其可承受的载荷不小于110 kg。理论和实验研究的结果均证实了这种指向系统的可行性和有效性。研究结果也表明这种单级控制的高精度指向系统存在以下特点:

1) 非对称性。指向系统具有两个不同的分支形式,因此理论仿真和实验误差数据均出现不对称形态,这种不对称的形态如图11、图12、图15和图16 所示。但机构的工作空间是对称的形态,图19 为该系统空间坐标系中的指向位置,因此这种非对称性并不影响指向系统的功能。

图19 空间坐标系中的指向位置

2) 指向精度表现出对惯量的敏感性。RPS-SPS并联机构通过中间球铰副消除了载荷重量对分支的作用,这使载荷惯量成为影响精度的主要因素之一。载荷惯量和其质量成正比关系,因此原型机在加载状态下的指向误差大于空载下的数值。通过对比图11 和图15、图12和图16,可以得出以下结果:仿真的指向误差小于空载的误差,而空载的误差又小于加载的误差,理论计算和实验数据均证实了这个特点,因此减少载荷质心到中心球铰的距离能有效提高指向精度。

3) 指向精度表现出对振动的敏感性。当原型机周围存在振动扰动时,测试的误差也明显增大,研究也表明振动环境能对指向精度产生严重扰动[31],这也是测试数据比仿真结果表现出更大离散性的原因之一。

4) 指向稳定时间表现出对载荷不敏感的特性。在两种载荷状态下,大部分位置点的稳定时间都小于30 ms,只有少数位置点的稳定时间接近于100 ms。 图18表明空载和加载状态下的实验数据基本一致,这说明双模型比较误差消除算法起到了作用。

综合以上的分析,本文提出的这种高精度指向机构在大载荷下依然有很好的响应特性,这得益于其稳定时间对载荷不敏感的特点,但需要考虑载荷惯量对指向精度的影响,通过降低载荷质心位置减少了该影响,最终的技术方案匹配了某系统的功能要求,也满足了大载荷、高精度的性能指标。

4 结论

基于消除指向机构的位置浮动环节可提高指向精度的原理,本文研究了一种单级控制的高精度指向系统,可实现大负载、高精度的指向性能。得出以下主要结论:

1) 指向系统原型机在110 kg的载荷下,其达到的性能指标为:单轴误差≯0.004°,空间合成误差≯0.006°,指向稳定时间≯100 ms,工作空间为两轴±9°。

2) 消除并联机构的中间位置浮动环节可有效提高指向精度。研究的指向系统采用了一种无中间位置浮动环节的RPS-SRS并联指向机构以及双模型比较法的误差消除算法,其理论和实验结果均验证了该设计思想的正确和有效性。

3) 原型机的实验结果表明振动环境会对指向造成扰动,振动抑制能改善原型机的指向精度。RPS-SRS并联指向机构及其信号处理系统中的振动抑制技术成为研制工程样机的重要环节。