高超声速攻防博弈自适应微分对策三维制导

王子瑶, 唐胜景, 郭杰, 阎宏磊, 葛健豪

(北京理工大学 宇航学院, 北京 100081)

0 引言

高超声速飞行器具有飞行速度快、可自主博弈机动等突出特点,其作为进攻性武器具有很强的突防能力,现有防空反导系统对高超声速目标的拦截效能较低,不具优势[1]。2018年,美国国防高级研究计划局探究新型作战空天拦截方案,启动“滑翔破坏者”项目,旨在使用高超声速滑翔飞行器(HGV)远距离精确拦截高超声速目标,并于2021年完成了项目技术演示的关键设计审查和飞行试验的可行性研究[2-3]。使用HGV作为高超声速拦截器对高超声速目标进行拦截具有以下优势:

1)HGV在速度和机动性方面与高超声速目标相当甚至更具优势,可以避免采用多拦一的拦截策略,提高效费比。

2)HGV具备远程制导拦截的能力,可在远离我方阵地处对高超声速目标进行有效毁伤,避免了拦截后的附加伤害。

3)高超声速目标飞行轨迹位于现有防空反导系统的拦截“盲区”高度[4],使用HGV再入拦截可以弥补这一空窗高度。

4)HGV可以自上而下再入拦截高超声速目标,有利于增加导引头探测距离,创造更大的拦截窗口[5]。

本文以HGV作为高超声速拦截器,其拦截高超声速目标的作战流程示意图如图1所示。在探测到高超声速目标后,拦截器经过助推段开始无动力滑翔再入,在初始下降段和滑翔段依靠卫星进行目标探测,进入末制导段后依靠自身导引头探测目标并实施最终打击。本文在末制导段为HGV设计可精确拦截高超声速目标的先进制导律。

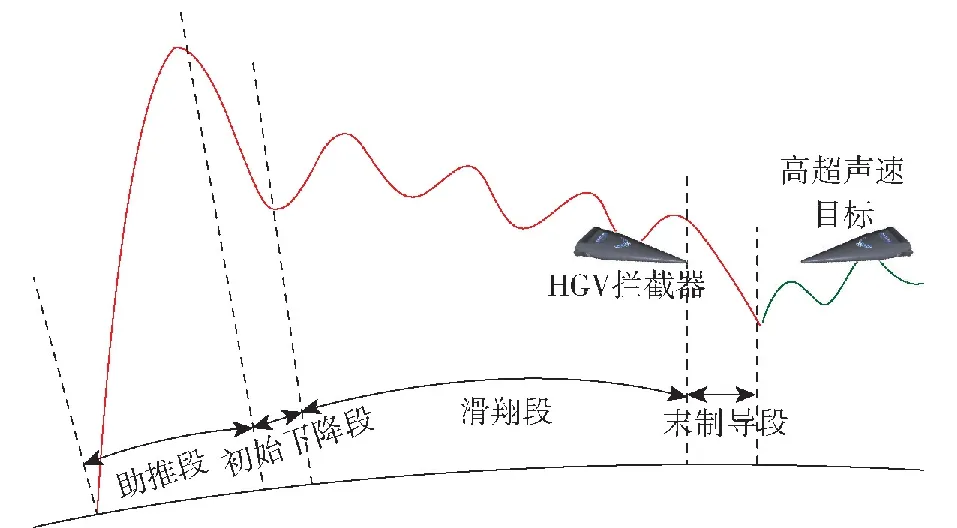
图1 HGV拦截高超声速目标的作战流程示意图

而高超声速目标能够进行主动机动,面对拦截可以采取智能的躲避策略,所以进行高超声速攻防博弈制导律研究是十分必要的[6]。攻防博弈即攻防双方在已知信息和约束的基础上利用各自能力展开博弈,以获取各自的最大利益[7]。现有攻防博弈研究对象主要集中在无人机对抗[8]、传统战术弹攻防[9]、航天器交会[10]等,关于高超声速飞行器攻防博弈的研究较少。文献[11]中针对吸气式高超声速飞行器与从同一方向连续来袭拦截弹之间的博弈问题,在过载约束下设计了躲避拦截的最优制导律。文献[12]在战术弹拦截吸气式高超声速巡航目标的末制导问题中基于直觉模糊的动态博弈模型,结合多属性评估方法和支付矩阵直觉模糊表示,求解博弈双方动态策略。

攻防博弈问题是一个典型的双边最优问题,当前对该问题的求解方法集中在了微分对策理论,即考虑攻防博弈双方的最优策略[13]。微分对策理论最早由Issacs[14]提出,后续Friedman[15]严格证明了微分对策值与鞍点的存在形式,从而奠定了微分对策坚实的理论基础。文献[16]证明了高超声速目标采用微分对策制导律相比正弦机动等传统策略更容易躲避拦截。文献[17]对高超声速弹头躲避动能拦截器的二人零和微分博弈问题,基于微分对策理论构建最优策略集,得出弹头的最优规避策略。文献[18]对导弹在大气层外拦截高超声速目标进行分段小扰动线性化,通过求解Riccati微分方程设计了微分对策制导律。文献[19]为有效拦截高超声速飞行器目标,以非线性模型预测控制为框架,采用梯度下降法求解拦截弹的有限时域微分对策三维制导律。

微分对策制导的核心是求解Hamilton-Jacobi-Isaacs(HJI)方程,但HJI方程一般为形式复杂的偏微分方程,无法直接获得解析解。而自适应动态规划(ADP)利用神经网络估计代价函数,并且具有求解速度快、计算精度高等优点,能够很好地应用于攻防博弈制导律求解过程。目前,ADP在飞行器制导领域的应用成果较少,研究主要针对低速导弹[20]。文献[21]采用策略迭代ADP算法,求解了攻防博弈系统模型未知情况下的近似最优策略。文献[22]对存在不确定项的导弹攻防零和微分对策问题,利用ADP算法提出了鲁棒自适应最优控制方案。文献[23]则利用ADP算法设计了输入饱和条件下的有限时间微分对策制导律。ADP算法在高超声速攻防博弈问题上的应用比较少见。文献[24]对高超声速目标拦截问题进行了微分对策建模,并基于双启发式的ADP算法求取了纳什均衡解。但其建立在攻防双方速度不变的假设上,未考虑高超声速飞行器真实的动态特性。

本文将HGV作为攻防博弈的双方,在末制导段设计了基于ADP算法的高超声速攻防博弈自适应微分对策三维制导律。根据HGV制导特性,将高超声速攻防博弈三维制导问题分解到纵向平面和侧向平面内。在不忽略高超声速动态特性的前提下,建立纵向二人零和微分博弈问题模型,设计非二次型代价函数保证攻防博弈双方控制量在约束内,引入评价神经网络拟合最优代价函数并求解HJI方程,得到微分对策倾侧角幅值指令。侧向制导则基于平行接近法得到航向角参考指令,并设计倾侧角反转逻辑对参考指令进行跟踪。最后通过HGV攻防博弈仿真算例验证所设计制导律的有效性和优越性。

1 高超声速攻防博弈双方运动模型

本文考虑高超声速飞行器三维攻防博弈问题,拦截器试图拦截目标,而目标试图躲避拦截器,博弈双方均以HGV为研究对象,攻防博弈几何关系如图2所示。忽略地球曲率及其自转效应,HGV在东北天坐标系Oxyh中的运动方程为

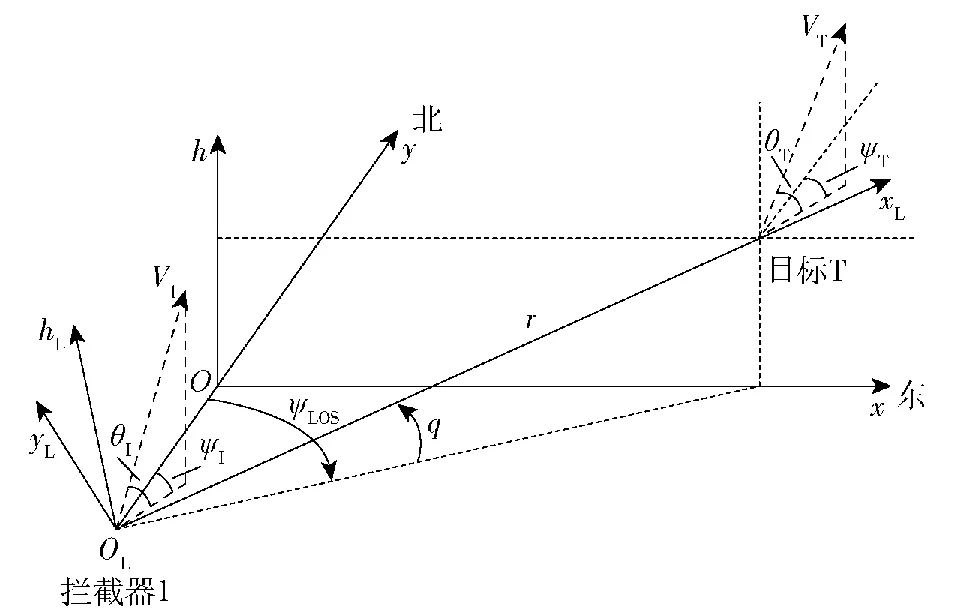
图2 攻防博弈几何关系

(1)

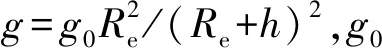
(2)

ρ为高度决定的大气密度,ρ=ρ0exp (-h/hs),ρ0为海平面处的大气密度,hs为标准高度,CL和CD分别为攻角α和马赫数Ma确定的升力系数和阻力系数,Sref为HGV的特征面积。图2中,为区分攻防博弈双方,高超声速拦截器相关变量带有右下标I,高超声速目标相关变量带有右下标T,r为拦截器和目标之间的相对距离,q为纵向视线角,ψLOS为侧向视线角,以正北方向顺时针方向为正。

首先建立视线坐标系OLxLyLhL,如图2中所示。视线坐标系原点OL取在拦截器处;OLxL轴与弹目视线重合,指向目标为正;OLyL轴在水平面内与OLxL轴垂直,从拦截器向目标方向看,指向左侧为正;OLyL轴垂直与OLxLyL平面,方向按右手直角坐标系确定。东北天坐标系Oxyh到视线坐标系OLxLyLhL的转换矩阵为

(3)

则高超声速拦截器速度在视线坐标系中的投影VIx、VIy、VIh为

(4)

同样地,高超声速目标速度在视线坐标系中的投影VTx、VTy、VTh为

(5)

则高超声速拦截器和目标的相对运动关系为

(6)

由于HGV无动力滑翔再入过程速度不断下降,在滑翔段速度下降到一定值后开始采用最大升阻比攻角飞行,可以达到较大航程[25],实现远程拦截效果,所以假设本文中高超声速拦截器与目标均采用常值最大升阻比攻角飞行,即αI=αIL/D、αT=αTL/D。高超声速拦截器和目标分别通过控制倾侧角σI和σT的幅值进行纵向机动,通过倾侧角反转改变倾侧角符号进行侧向机动。本文将分别设计攻防博弈双方的纵向自适应微分对策制导律和侧向平行接近倾侧角反转逻辑,实现高超声速拦截器对灵活机动躲避打击的高超声速目标的精准拦截。

2 高超声速纵向自适应微分对策制导

2.1 高超声速二人零和微分博弈问题

首先引入零控脱靶量的概念,即高超声速拦截方和目标均不再发生机动时的最小距离[26],表达式为

(7)

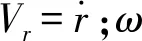
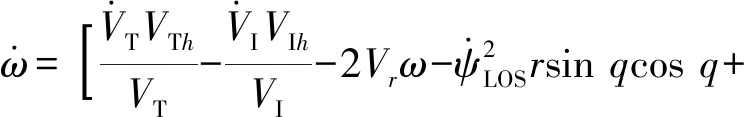
(8)

选取高超声速拦截器的纵向法向加速度u和目标的纵向法向加速度v作为高超声速攻防博弈系统的虚拟控制输入,其表达式为

(9)

于是式(8)可整理为

(10)

式中:

在高超声速攻防博弈过程中,为了能够成功拦截目标,拦截方会通过选择控制策略u最小化零控脱靶量,而目标会调整自己的控制策略v最大化零控脱靶量,试图逃逸[22]。则高超声速攻防博弈系统式(10)为二人零和微分博弈问题,即博弈其中一方试图最小化设计的代价函数,而另一方使其最大[27]。

假设1假设式(10)中g(ω)和h(ω)均有上界,即存在两个正常数gm和hm,使得|g(ω)|≤gm、|h(ω)|≤hm成立。

为避免弹目距离趋近于0 m引起的高超声速攻防博弈双方终端状态和控制量发散,当高超声速拦截器与高超声速目标相对距离小于距离rf时,不再进行机动,制导策略采取零值,因此有|g(ω)|≤1/rf、|h(ω)|≤1/rf,故假设1成立。

2.2 高超声速微分博弈最优策略

基于高超声速攻防博弈系统的二人零和微分博弈问题式(10)建立合适的代价函数,求取纳什均衡解。高超声速拦截器的控制输入目的是最小化代价函数,而目标的控制输入则试图最大化代价函数。由式(9)可知,当高超声速拦截器和目标的倾侧角为0°时,博弈双方的升力全部用来提供纵向法向加速度,法向加速度达到最大值。当法向加速度超过最大值时,将造成倾侧角幅值无解的情况。为了保证博弈双方倾侧角幅值始终有解,设计二人零和微分博弈问题式(10)的代价函数[28]为非二次型形式:

(11)

式中:Q为代价函数权重,为一正常数;UJ(u)、VJ(v)均为处理控制约束的非二次型泛函,设计为

(12)

R1、R2为代价函数权重,λ1、λ2为控制增益,均为正常数,φ(·)为满足φ(·)≤1、φ(0)=0的一一映射连续有界Cε(ε≥1)类函数,且其为1阶导数有界的单调奇函数[29],φ-1(·)代表φ(·)的反函数。函数φ(·)可映射施加的控制约束,并且已被证明此类函数能满足最优解在控制约束内[30]。由于双曲正切函数满足要求且积分形式简单,选择φ(·)=tanh (·),则式(12)可表达为

(13)

对式(13)求积分,可得

(14)

为求取代价函数式(11)的最优控制策略,建立二人零和微分博弈问题式(10)的Hamilton函数为

(15)

根据Nash-Pontryagin极大极小值原理,Hamilton函数式(15)的纳什均衡解(u*,v*)存在的必要条件[31]为

H(u*,v)≤H(u*,v*)≤H(u,v*)

(16)

二人零和微分博弈问题式(10)的最优代价函数J*满足如下关系式:

(17)

可通过求解Hamilton-Jacobi-Isaacs(HJI)方程得到,即

(18)

为使HJI方程式(18)的解存在且唯一,利用最优控制必要条件∂H(u,v)/∂u=0和∂H(u,v)/∂v=0,可得到攻防博弈双方的纳什均衡解为

(19)

2.3 基于ADP的微分对策制导律

将最优控制策略式(19)代入式(14),可得攻防博弈双方的非二次型泛函为

(20)

进一步,将攻防博弈双方的最优控制策略式(19)和非二次型泛函式(20)代入HJI方程式(18)中,整理可得

(21)

由此可见,HJI方程式(21)为关于最优代价函数J*的非线性偏微分方程,难以得到解析解。为解决这一问题,通过ADP方法,利用神经网络的非线性逼近能力[29],构建权值在线更新的评价神经网络对最优代价函数J*进行逼近。

评价神经网络为反向传播(BP)神经网络,其结构图如图3所示,仅采用一层隐藏层。BP神经网络的输入仅为纵向视线角速率ω,输出即为最优代价函数J*的估计值,其存在一个理想评价神经网络,即

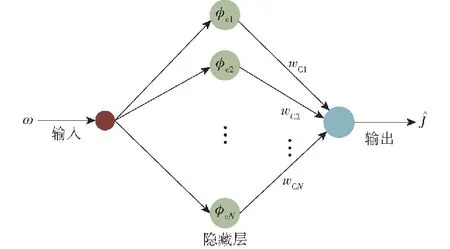
图3 评价神经网络结构图

(22)

ΦC(ω)=[φC1(ω),…,φCi(ω),…,φCN(ω)]T

(23)

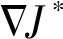
(24)

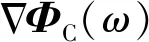
将式(24)代入最优控制策略式(19),可得

(25)

式中:

(26)

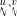
(27)

式中:εHJI为由评价神经网络逼近误差引起的残余误差,其表达式为

(28)

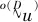
根据文献[29],随着神经元个数N的不断增加,剩余残差εHJI逐渐收敛到0。即对于一个任意正数εHJIm>0,总是存在一个正数N′,使得当N>N′时,|εHJI|≤εHJIm。

但是估计最优代价函数J*的理想评价神经网络是未知的,只能利用神经网络拟合逼近最优代价函数,即

(29)

式中:WC为评价神经网络的估计权值向量,WC=[wC1,wC2,…,wCN]T∈RN。式(29)对纵向视线角速率ω的偏导数为

(30)

于是可得估计的微分对策控制策略为

(31)

式中:

将式(31)代入Hamilton函数式(15),可得到估计的Hamilton函数为

(32)

(33)

式中:αC、αW为学习率,αC,αW>0。式(33)中等号右边第1项由梯度下降法得到,可使估计的Hamilton函数最小化,第2项为权值反馈项,有利于权值向量更快地收敛。令β=∂eC/∂g(ω)+h(ω)],则评价神经网络估计误差的变化率为

(34)

评价神经网络无需进行离线训练,其权值向量进行在线更新。评价神经网络的输入仅为纵向视线角速度ω,权值更新律式(33)亦为与纵向视线角速度ω有关的函数。纵向视线角速度ω通过拦截器的导引头即可测得,具有一定的工程实现性。

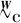
证明选择Lyapunov函数为

(35)

(36)

针对式(36)等号右侧第1项:

(37)

由HJI方程式(27),可得

(38)

式中:

基于假设条件,易得ε1是有界的,即存在常数ε1m满足|ε1|≤ε1m。

(39)

式中:

(40)

针对式(36)等号右侧第2项:

(41)

由HJI方程式(27),可得

(42)

由泰勒展开式

(43)

式中:

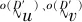
(44)

(45)

进一步,式(36)可变换为

(46)

(47)

于是由式(9)和式(31)可得高超声速博弈双方的倾侧角幅值指令为

(48)

3 高超声速侧向平行接近倾侧角反转制导律

侧向制导律采用航向角走廊方法[33-34]确定倾侧角符号。首先通过平行接近法确定博弈双方的参考航向角,然后在参考航向角两侧建立宽度为Δψ的航向角走廊。当HGV的航向角超出航向角走廊时,倾侧角反转改变符号;当航向角未超出航向角走廊,保持倾侧角符号不变[35]。

对于高超声速拦截器,为使攻防博弈双方在侧向平面内满足平行接近关系,需博弈双方速度满足

VIy=VTy

(49)

代入式(3)～式(5)可得高超声速拦截器的参考航向角为

(50)

则高超声速拦截器的倾侧角反转逻辑为

(51)

式中:σ′I为上一时刻高超声速拦截器的倾侧角;Δψ为航向角走廊宽度,其表达式为

Δψ=(Δψ2-Δψ1)r/r0+Δψ1

(52)

Δψ1和Δψ2为常值系数,且0<Δψ1≤Δψ2,r0为初始弹目距离。航向角走廊宽度随着弹目距离减小而不断减小。

对高超声速目标来说,为使博弈双方侧向速度保持平行但相互远离,博弈双方速度需满足

VIy=-VTy

(53)

由式(3)～式(5)可得,高超声速目标的参考航向角为

(54)

同样地,高超声速目标的倾侧角反转逻辑为

(55)

式中:σ′T为上一时刻高超声速目标的倾侧角。

4 仿真与分析

以高超声速拦截器对来袭高超声速目标进行拦截为背景进行仿真,高超声速拦截器和目标均以美国通用航空器CAV-H[36]为仿真对象,双方最大升阻比攻角αIL/D=αTL/D=20°。为验证本文所设计制导律的有效性,设计3个高超声速目标拦截任务进行仿真,分别记作任务1～任务3。在各拦截任务中,高超声速拦截器初始状态不变,高超声速目标的初始位置和初始速度相同,但初始航迹角和航向角不同。双方初始状态如表1所示。为了提现本文所设计微分对策制导律的优越性,将比例导引制导律作为对比方法,对比方法中纵向制导利用比例导引律确定倾侧角幅值,比例导引系数为3,侧向制导采用本文提出的平行接近倾侧角反转制导律,高超声速目标仍然按照微分对策制导指令飞行。

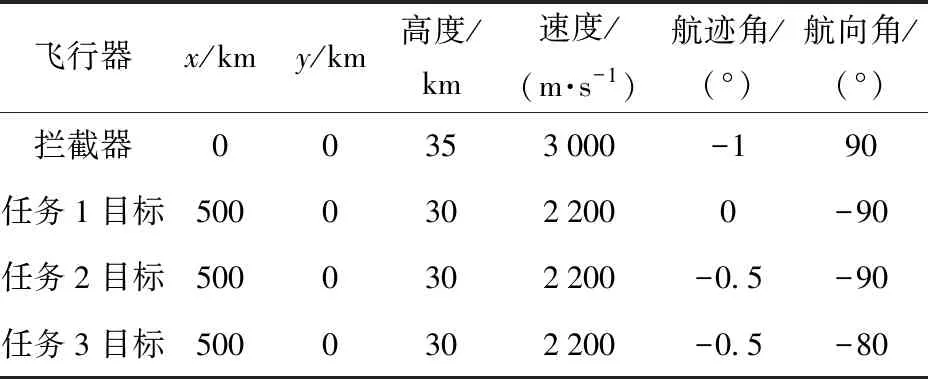
表1 攻防博弈双方的初始状态

纵向自适应微分对策制导中,代价函数权重选取为Q=10、R1=0.003、R2=0.001,控制增益选取为λ1=0.4、λ2=0.4,评价神经网络为BP神经网络,激励函数选取为ΦC(ω)=[ω,ω2,ω3,ω4]T,初始的估计权值向量选取为WC=[-100,-100,-100,-100]T,评价神经网络学习率αC=1×108、αW=0.01。当博弈双方相对距离小于rf=1 km时,开始采取零值法向加速度。侧向平行接近倾侧角反转制导中,航向角走廊宽度系数选取为Δψ1=0.5°和Δψ2=3°。

仿真结果如图4～图12所示。由图4所示的攻防博弈双方三维轨迹曲线可以直观地看到各任务中,本文所设计的微分对策制导律和比例导引制导律均能够使高超声速拦截器成功命中高超声速目标。但在图5所示的纵向法向加速度曲线中,高超声速拦截器采用微分对策制导律所需法向加速度明显小于比例导引律。图6展示了ADP算法估计的Hamilton函数值,值并未逐渐减小是由评价神经网络权值更新律包括权值反馈项导致的,但 Hamilton函数值始终保持在零值附近,验证了评价神经网络对最优代价函数逼近的正确性。各拦截任务中的评价神经网络权值如图7所示,可见权值wC1最终稳定于零值。由于权值wC2、wC3、wC4更新律中包含纵向视线角速率ω的高次幂,而由图8(c)所示的纵向弹目视线角速率曲线可以看出,各拦截任务中纵向视线角速率基本都保持在0 rad/s,所以权值wC2、wC3、wC4的更新律受到ω的影响较小,变化趋势主要由权值反馈项决定。图8(a)展示了微分对策制导下,高超声速拦截器和目标的相对距离曲线,显示出在本文所提出的制导律作用下,拦截器能够在目标机动的情况下不断接近目标,各任务中攻防博弈双方的最终距离分别为6.78 m、7.77 m、4.18 m,均达到了米级精度,实现了精确打击。图8(b)为纵向弹目视线角曲线,可见纵向视线角基本上都保持恒定,直到最后时刻弹目距离很小时才发散。高超声速拦截器和目标的速度如图9所示,由于阻力的存在,攻防博弈双方速度均大幅度减小。图10为高超声速拦截器和目标的航迹角,最后时刻为了避免由于相对距离趋近于0 m而引起的神经网络权值发散问题,纵向法向加速度采取零值,所以最后时刻攻防博弈双方的航迹角保持不变。图11展示了高超声速拦截器和目标的航向角曲线,拦截器通过不断改变倾侧角符号进行侧向制导逼近目标,而目标航向角未超出其航向角走廊边界,一直力求朝着远离拦截器的方向飞行。图12为攻防博弈双方的倾侧角,可见双方倾侧角在博弈过程中始终有解,故满足控制约束。随着弹目距离减小,航向角走廊宽度也逐渐减小,高超声速拦截器的倾侧角反转频率逐渐加快。高超声速目标的倾侧角幅值是逐渐减小的,这是由于随着弹目距离不断减小,目标采取减小倾侧角策略而得到更大的升力,进而得到更大的纵向、法向加速度以躲避拦截器,但拦截器最终仍能够成功命中目标。

图4 攻防博弈双方的三维轨迹

图5 攻防博弈双方的纵向法向加速度

图6 ADP算法估计的Hamilton函数值

图7 ADP算法评价神经网络权值

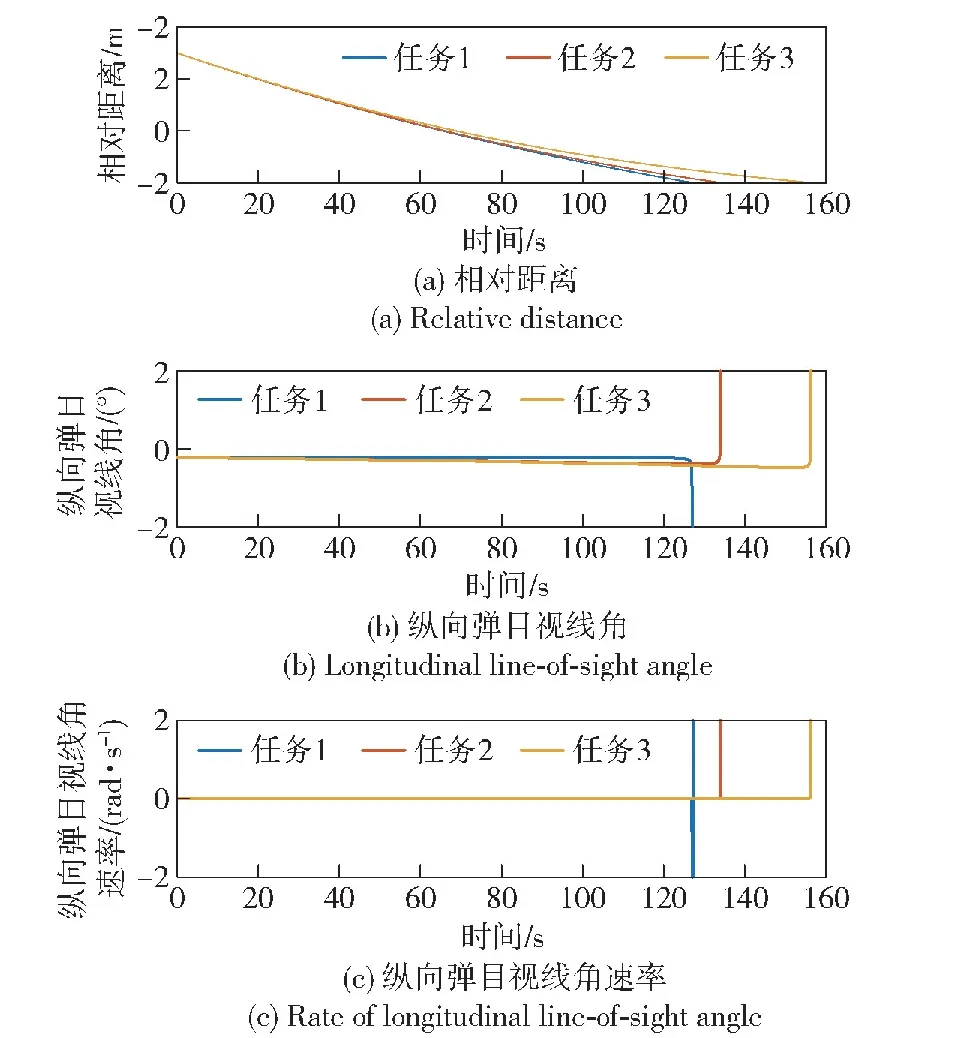
图8 微分对策制导下攻防博弈双方的相对关系

图9 微分对策制导下攻防博弈双方的速度

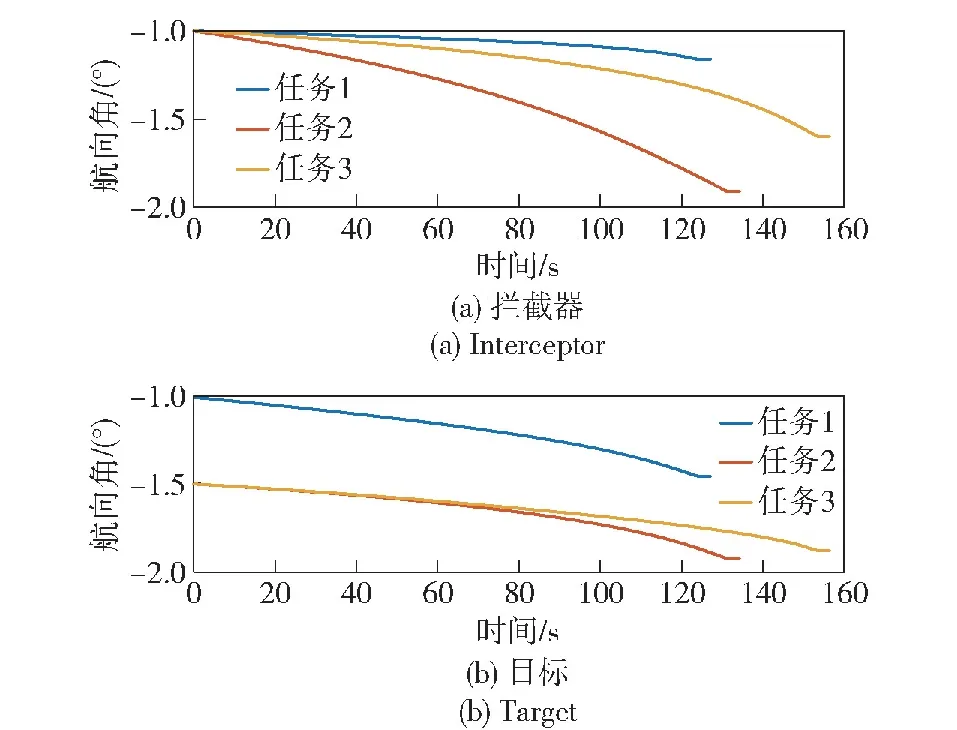
图10 微分对策制导下攻防博弈双方的航迹角

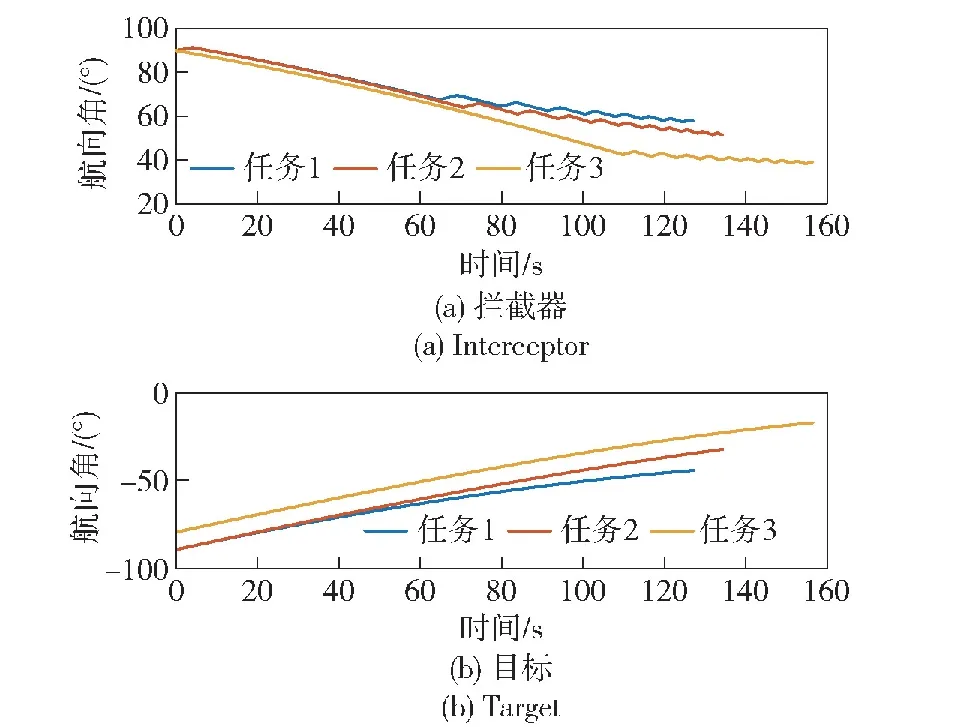
图11 微分对策制导下攻防博弈双方的航向角

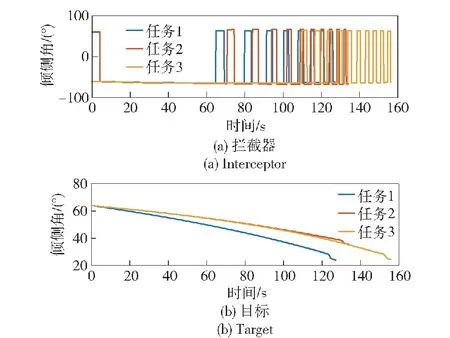
图12 微分对策制导下攻防博弈双方的倾侧角

各拦截任务的仿真是在配有Intel(R) Core(TM) i5-8265U CPU @ 1.60 GHz、8.00 GB内存的仿真计算机上进行,仿真计算用时分别为2.83 s、2.95 s、3.48 s,可以满足在线制导的实时性要求。

5 结论

本文基于ADP算法对高超声速拦截器打击高超声速机动目标的攻防博弈系统进行自适应微分对策三维制导律设计。在纵向平面内建立了高超声速二人零和微分博弈问题模型,设计了非二次型代价函数,并通过求解HJI方程,引入评价神经网络逼近最优代价函数,得到了高超声速拦截器和目标的微分对策制导指令。在侧向平面内,通过平行接近制导法为攻防博弈双方提供参考航向角指令,并基于倾侧角反转逻辑实现了侧向制导。得出的主要结论如下:

1)本文以HGV为攻防博弈双方对象,在攻防博弈三维制导律设计中考虑了高超声速飞行器动态特征,在不忽略攻防博弈双方速度变化率的前提下建立了高超声速二人零和微分博弈问题。

2)相比于比例导引制导律,本文提出的微分对策制导律所需要的法向加速度更小,且能够实现高超声速拦截器对机动躲避拦截的高超声速目标的精准打击。

3)设计了非二次型代价函数保证攻防博弈双方满足控制约束,使得攻防博弈双方的倾侧角指令始终有解。

本文后续工作可进一步拓展微分对策制导的应用场景,应用于HGV滑翔段等多个飞行阶段,并针对高超声速巡航目标等多种机动目标进行拦截制导。此外,可在本方法基础上考虑攻击角度约束及障碍约束,实现多约束条件下的高超声速攻防博弈制导。