基于DNA动态编码和VMP-WFRFT的安全通信方法

王西康, 孟庆微, 许华, 齐子森, 张悦

(空军工程大学 信息与导航学院, 陕西 西安 710077)

0 引言

信息安全是国家安全的重要组成部分,涵盖了通信安全、系统安全以及网络安全等多个方面。无线通信物理层安全通信技术[1],颠覆了上层加密方案以计算复杂度换取安全性的做法,能够通过物理层加密、人工噪声、波束成形等方式保障信息在无线传输过程中的安全,使窃听者无法有效窃取、破译合法信息,是当前无线通信领域的一个热点问题。

混沌系统因具备伪随机性、对初值敏感性以及难以预测等特点在信号加密领域开展了广泛研究。文献[2]提出了一种基于Hénon映射相位旋转和子载波随机选择的安全传输方法。文献[3]提出利用改进的Logistic混沌序列产生随机相位旋转矩阵对多参数加权分数傅里叶变换(MP-WFRFT)信号进行相位加扰。然而低维混沌映射存在迭代方式简单,易被预测等问题。因此,研究人员利用高维混沌系统[4-5]的复杂混沌序列进行算法设计,用于确保信息安全。但实际上,高维混沌系统结构复杂,会不可避免地造成较大计算损耗,且基于单一混沌映射设计的加密算法不足以确保信息传输的高安全性。

DNA编码是生物信息领域研究的一个热点,在数据加密、隐藏、认证等技术领域具备广阔的研究前景,尤其在图像加密[6-8]等领域展现出了其优异的性能。将混沌系统与DNA相结合可以降低其编码规则少所带来的安全隐患。文献[6]提出利用混沌随机序列动态选择DNA编码规则以及作为约瑟夫遍历的变步长,该加密算法能有效抵御统计性分析和穷举分析等攻击操作。文献[7]提出将图像处理为DNA序列,并与构建的S盒进行DNA运算,最后利用超混沌序列进行图像置乱。本文通过将DNA编码引入比特加密,可从比特编码层面显著提高物理层的安全性。考虑到基于混沌和DNA的加密方法只能停留在比特层面,对于信号传输过程中的调制样式无法掩盖,为进一步提升信号传输的加密性能,采用改进的变化多参数加权分数傅里叶变换(VMP-WFRFT)对已调信号的星座实施置乱和扩散,这也是DNA编码与WFRFT通信系统的首次结合。WFRFT是一种特性良好时频数学工具,其过程实现简单,且经过WFRFT后的信号星座复杂,呈类高斯分布。WFRFT可用于星座预编码设计[9]、高斯标签嵌入[10]、掩盖信号生成[11]等安全通信算法中,相关研究人员也对其提出了一些新的改进[12-13]。然而目前关于WFRFT参数识别的研究[14-16]表明,在固定参数下,参数识别正确率可达到90%以上。因此将变参数更新策略用于MP-WFRFT是十分有必要的,可以极大提高MP-WFRFT的参数抗扫描性能。

综上所述,针对高维混沌巨大的计算开销、DNA编码样式准则少和MP-WFRFT固定参数易被识别等问题。本文将4个一维混沌系统嵌套使用在DNA动态编码过程中,降低混沌系统的计算损耗同时将DNA编码过程动态化,实现比特置乱。在保密信号调制样式上,利用混沌随机序列作为MP-WFRFT 的变化参数进行信号星座混淆、扩散,提高了MP-WFRFT参数抗扫描性能,整体上可归为从比特-信号两级加密的置乱-扩散机制通信方法。

1 混沌编码-域变换系统

1.1 混沌系统

Logistic混沌映射是一种应用十分广泛的非线性动力学离散混沌系统,但是基于单一Logistic混沌映射的加密算法存在密钥空间过小、含有大量弱密钥、产生的混沌序列分布不均匀等问题。文献[17]表明通过多混沌系统复合设计的加密算法能有效降低单一混沌加密算法的上述问题,强化密钥的随机性能,抵抗安全攻击,因此本文采用多混沌进行加密算法设计。LSS、LTS和TSS[18]等一维混沌映射是从Logistic映射演变而来的,具备良好的混沌特性和更大的混沌参数区间,各混沌映射的方程定义如下:

xn+1=Logistic(r1,xn)=r1xn(1-xn)

(1)

(2)

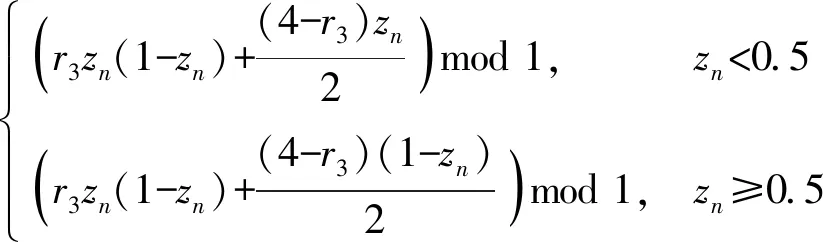
(3)

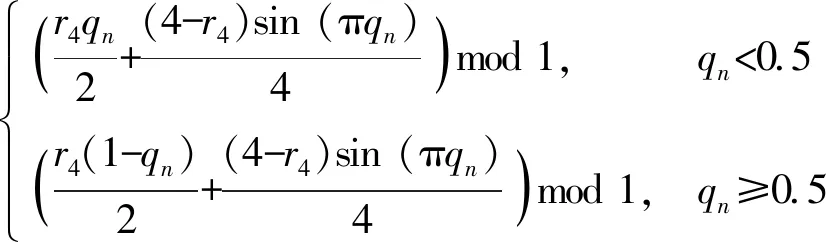
(4)

式中:x、y、z、q为状态变量;r1、r2、r3、r4为分岔参数;n为迭代次数。在Logistic映射中,当r1处于[3.6,4.0],系统进入混沌状态,而在LSS、LTS和TSS映射中,当r2、r3、r4的取值处于(0,4]区间内时,系统均为混沌态。将以上4个低复杂度的一维混沌系统嵌套在DNA动态编码过程中,不仅克服了高维混沌方程的高计算复杂度问题,同时满足了DNA编解码多阶段多操作的加密序列随机性。

1.2 DNA生物编码

DNA分子组成共包含4种脱氧核苷酸,腺嘌呤(A)、胞嘧啶(C)、鸟嘌呤(G)、胸腺嘧啶(T)。由于DNA编码种类的特殊性和对信息处理的规律性,适用于处理0、1数字信息,采取将“00”、“01”、“10”、“11”这样的2个数字一组作为进行操作的数据元。通过DNA碱基互补配对的原则可以发现共存在 8种规则的配对方式,如表1所示。在对DNA编码后的数据进行操作时,提供3种方式来进一步加强编码的程度,分别是DNA加法、DNA减法以及DNA异或,具体规则见表2、表3、表4。通过以上DNA编码和DNA操作完成了对原始信息流数据的加密,其中置乱和混淆这2个操作往往是隐式发生的,包含在上述过程之中。

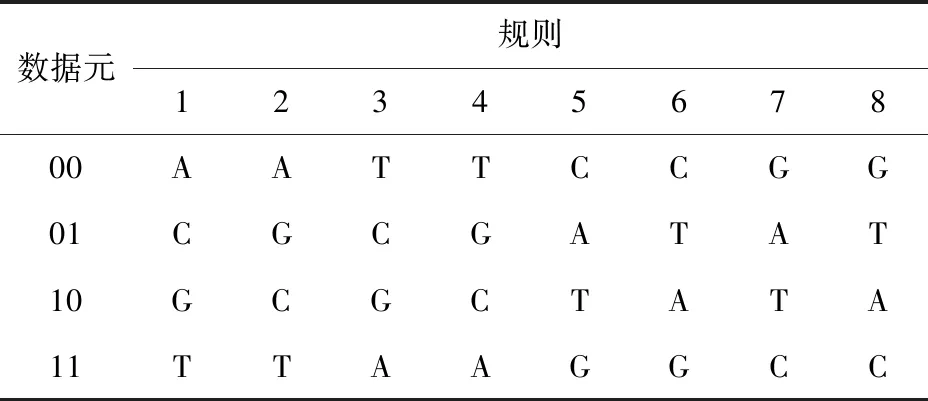
表1 DNA编码解码规则

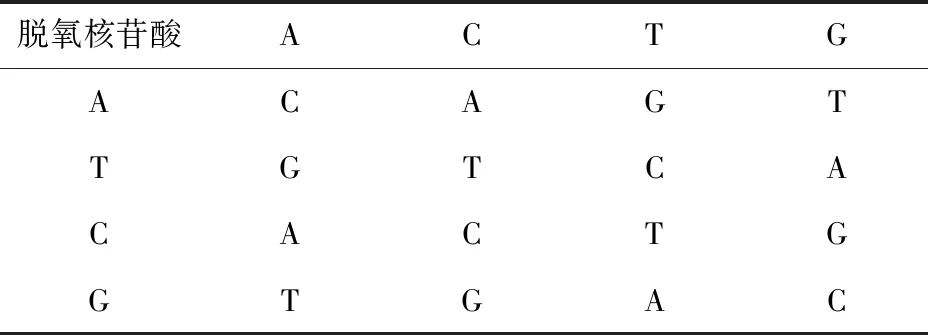
表2 DNA加法操作

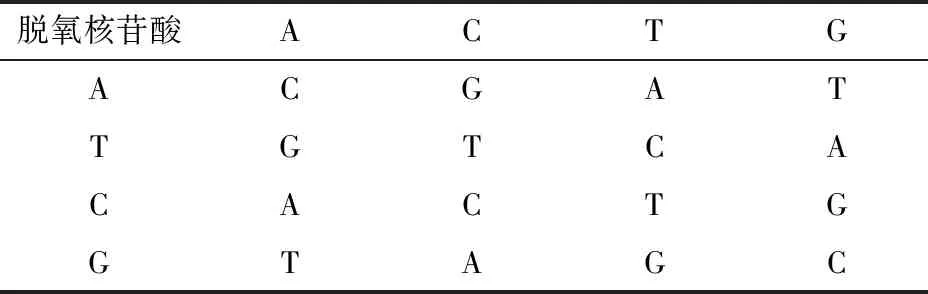
表3 DNA减法操作

表4 DNA异或操作

1.3 离散序列的多参数加权分数阶傅里叶变换

设X0是任意复数序列,分别对其进行1～3次离散傅里叶变换,结果分别为X1、X2、X3,MP-WFRFT的定义表示为

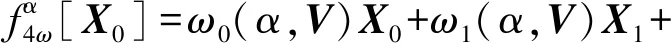
(5)

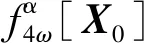
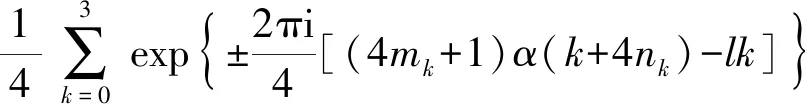
(6)

式中: i为虚数单位;mk、nk(k=0,1,2,3)构成尺度向量V= [m0,m1,m2,m3,n0,n1,n2,n3],通过调整变换阶数α和尺度向量V的取值来影响加权系数,进而使信号星座图发生旋转扩散。

2 加解密算法

基于DNA动态编码和VMP-WFRFT的通信系统框图如图1所示。发射端加密过程主要分为两个部分:第1部分为利用DNA动态编码系统对比特流信息进行加密;第2部分则为利用混沌序列控制MP-WFRFT阶数对QPSK调制后的信号进行星座加扰,接收端按照发射端相反顺序进行解密解调即可恢复出原始信号。

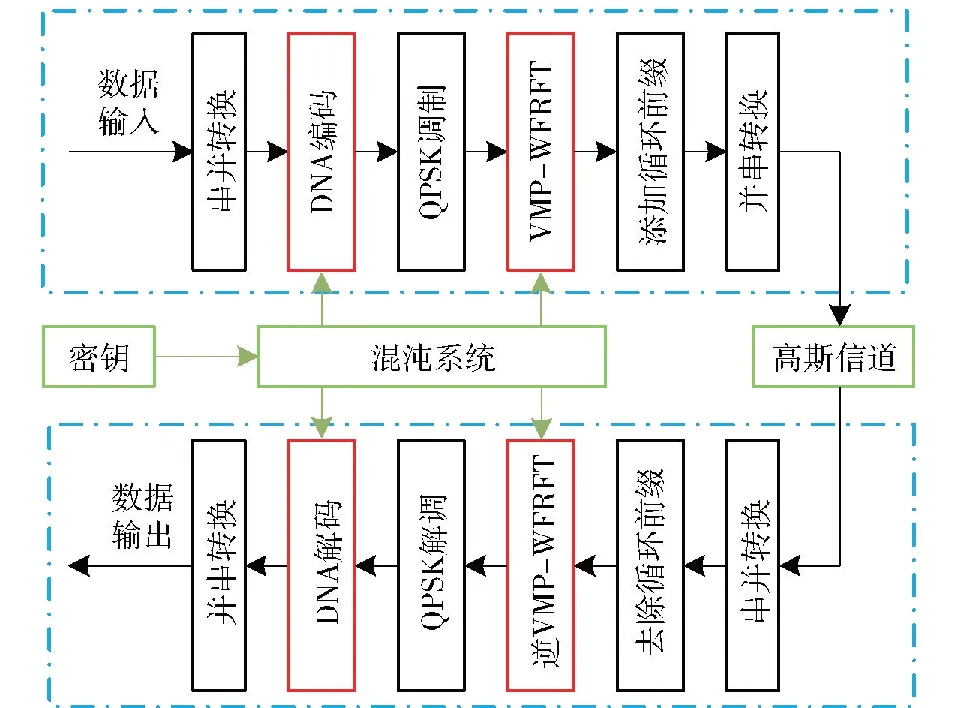
图1 基于DNA动态编码和VMP-WFRFT的通信系统框图

2.1 加密过程

本文主要针对信息在传输过程中的比特、信号两种状态进行分别加密,利用多维混沌系统融合至DNA编码多阶段多过程,对比特信息进行混淆,其次将Logtistic序列值代替MP-WFRFT的变换参数α,对已调信号星座分布进行加扰,变化的参数选择方式可以抵抗参数扫描。

具体的加密步骤为:

1) DNA动态编码。图2展示了DNA动态编码过程各阶段的具体操作,下面对其进一步进行阐述。由于四维混沌序列的取值都处于(0,1)区间,为了便于将序列值应用于加密各阶段,后续操作采取将混沌序列乘以1014后向下取整后,再进一步进行模运算。

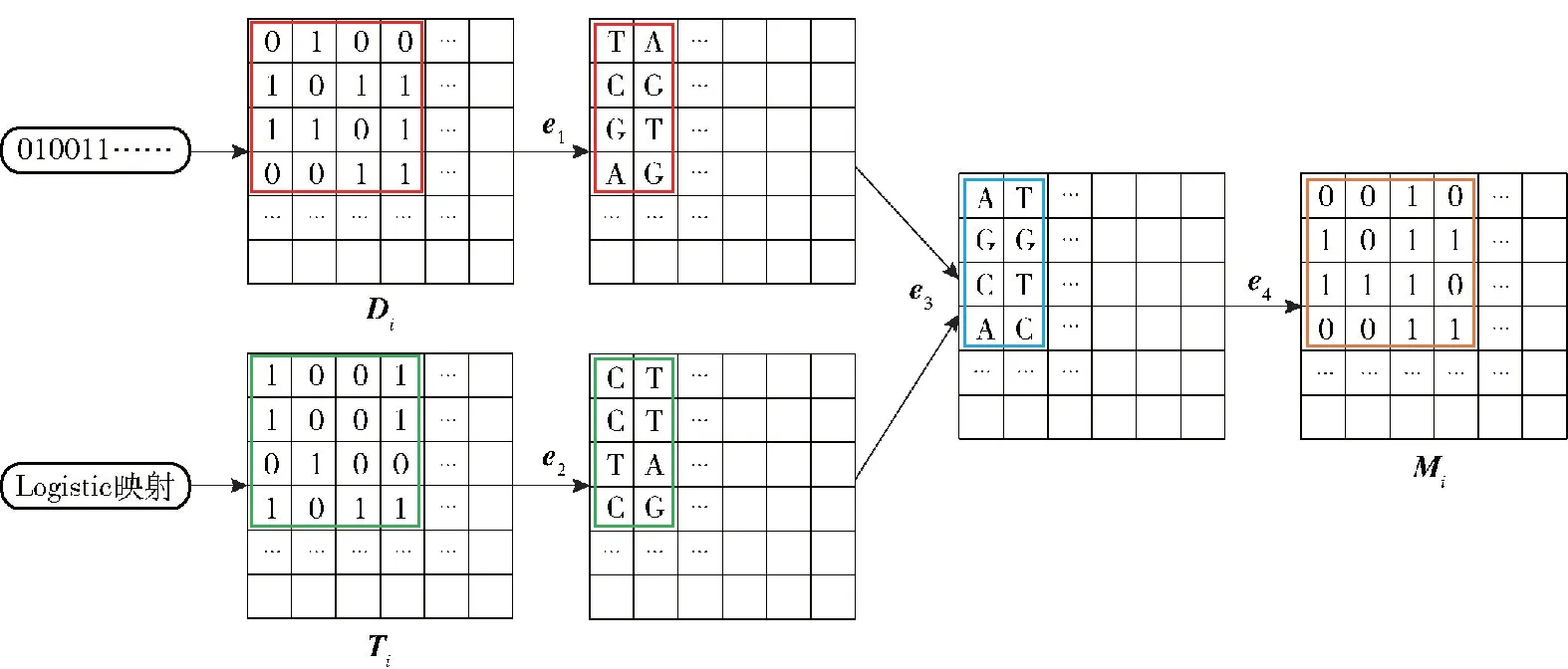
图2 DNA动态编码过程

首先,将原始信息流I,以长度H为单位进行分块,串并转换为大小g×g的矩阵Di,将其作为整个加密过程的基本操作单元。利用式(7)得到Di的密钥Pi,Pi用于生成Di对应密文模板Ti,通过Di与Ti的DNA加密操作生成密文信息Mi,由于密钥Pi来源于信息矩阵Di本身,能显著突出密钥的灵活性。

(7)

式中:ρ、λ为信息矩阵Di中比特值的位置索引。利用密钥Pi求得Ti的操作如下:Pi通过式(8)得到长度为H、取值为0,1的加密序列Bi,再进行串并转换为大小g×g的密文模板矩阵Ti。

Bi=mod (floor(Logistic(Pi,r1)×1014),2)

(8)

设置密钥(s1,s2,s3,s4,r1,r2,r3,r4)作为Logistic、LSS、LTS和TSS混沌系统的初值和参数,用于生成控制编码、运算、解码的浮点数ci(i=1,2,3,4)。

其中c1由(s1,r1)通过Logistic系统生成,c2由(s2,r2)通过LSS系统生成,c3由(s3,r3)通过LTS系统生成,c4由(s4,r4)通过TSS系统生成。Di和Ti的DNA操作是分块进行的,因此对Di和Ti再进行大小为t×t的分块处理后得到子块Dij、Tij,其中j为子块索引。ci中所包含序列的个数为分块大小t×t的矩阵个数U,如式(9)所示:

(9)

根据表1～表4,由于编码、解码方式有8种,运算方式有3种,因此通过式(10)将混沌系统产生在区间(0,1)内的ci(i=1, 2, 3, 4)搬移到集合{1, 2, 3, 4, 5, 6, 7, 8}和{1, 2, 3}上,得到控制序列码c′i(i=1, 2, 3, 4),用于DNA加密的各个阶段动态选择编码、解码以及运算方式,实现加密过程的动态化。

(10)

式中:e1用于控制Dij的编码方式;e2用于控制密文模板矩阵Tij的编码方式;e3用于控制Dij和Tij两个矩阵进行运算的操作方式,得出结果Vj,在运算过程中,每次还需利用Vj与Vj-1进行二次运算,实施扩散效果;e4用于控制Vj的解码方式。

Mij=[[Vj-1,[[Dij]e1,[Tij]e2]e3]e3]e4

(11)

式中:Mij为Dij加密后的信息。对Di加密后得到Mi。

2)VMP-WFRFT。将Mi展平为一维向量输入至MP-WFRFT,针对提升MP-WFRFT参数的抗扫描特性,利用密钥(s5,r5)生成Logistic混沌序列替代MP-WFRFT的固定参数α,同时结合固定值尺度向量[m0,m1,m2,m3,n0,n1,n2,n3]完成星座加扰,将变换后的信号加上循环前缀后经过并串变换,发送到AWGN信道上。

2.2 解密过程

解密过程是加密过程的逆过程,详细解密步骤如下所示:

1) 逆MP-WFRFT。接收方对接收到的信号进行去循环前缀、串并转换处理等操作,利用密钥(s5,r5)生成 Logistic 序列作为变换参数结合密钥[m0,m1,m2,m3,n0,n1,n2,n3]利用逆MP-WFRFT模块恢复QPSK调制星座图;

2) DNA解密。对进行QPSK解调后的数据进行DNA解密操作,经由并串转换后得到原始信息流。

3 实验与算法性能分析

3.1 混沌系统性能分析

混沌信号作为混沌加密算法的核心,其伪随机性能十分关键,混沌系统的初值灵敏度以及混沌序列的自相关、互相关值可以表征其伪随机特性的好坏。首先测试初值灵敏度,r1、r2、r3、r4的值设置为3.9,x、y、z、q的值设置为0.7。当x、y、z、q的初始值存在Δ=10-15的差异时,经过几十次迭代后,每两个混沌序列是完全不同的,Logistic、LSS、LTS和TSS的详细性能在图3中给出。其次,测试了4个混沌系统的自相关和互相关性能。获取长度为1 000的混沌序列,从图4(a)、图4(c)、图4(e)和图4(g)可以看出,仅序列自身自相关值等于1,其他时候,自相关值均接近0,这表明它们具有良好的自相关性能。互相关性能如图4(b)、图4(d)、图4(f)和图4(h)所示,从中可以看出,当给出初值当Δ=10-15的微小差异时,所有值的变化在[-0.1,0.1]中,这表明所产生序列互相关特性良好。

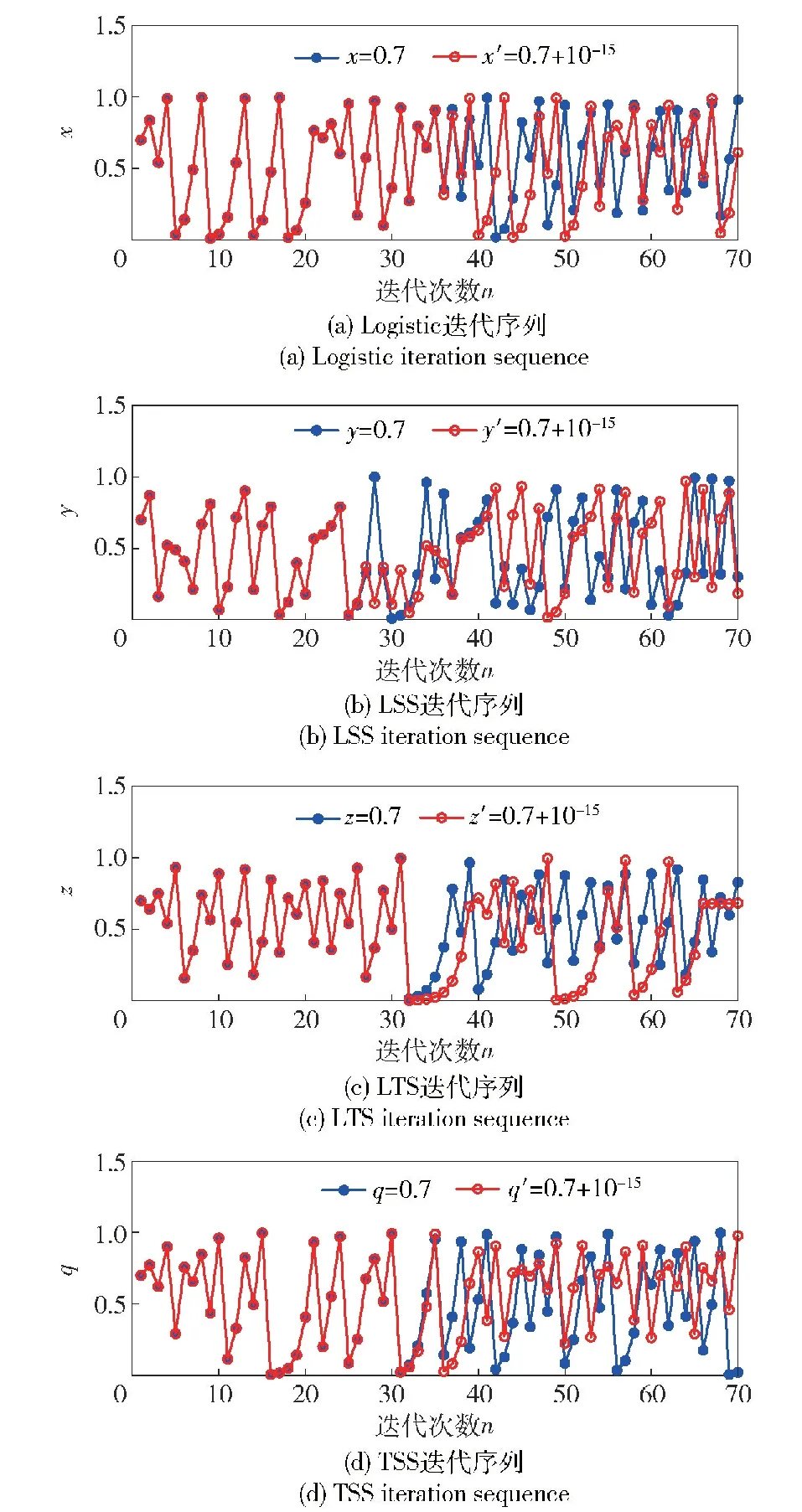
图3 混沌系统初值敏感度测试

表5将本文的混沌系统与其他高维混沌系统进行比较。由表5可以发现,本文使用的混沌系统具有较低的计算复杂度和较高的安全性且密钥空间较大,而文献[19-21]的超混沌系统采用4阶龙格-库塔方法,随着阶数的增加,伴随着较高的时间复杂度。

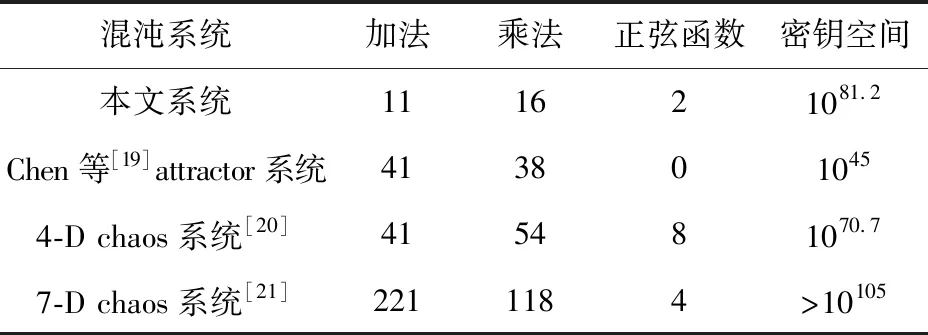
表5 不同混沌系统的比较

3.2 星座图裂变特性分析

MP-WFRFT可将不同调制样式下的星座分布转化为类高斯分布, 用于抵抗基于星座图案的调制信号识别。本文利用MATLAB软件进行了数值仿真。仿真信号的长度为65 535 bit,分块矩阵的大小设置为32×32,采用QPSK进行调制。设置MP-WFRFT参数V=0,分析变换阶数α为0、0.05、0.2和0.4不同取值下相对应的信号星座图,如图5 所示。

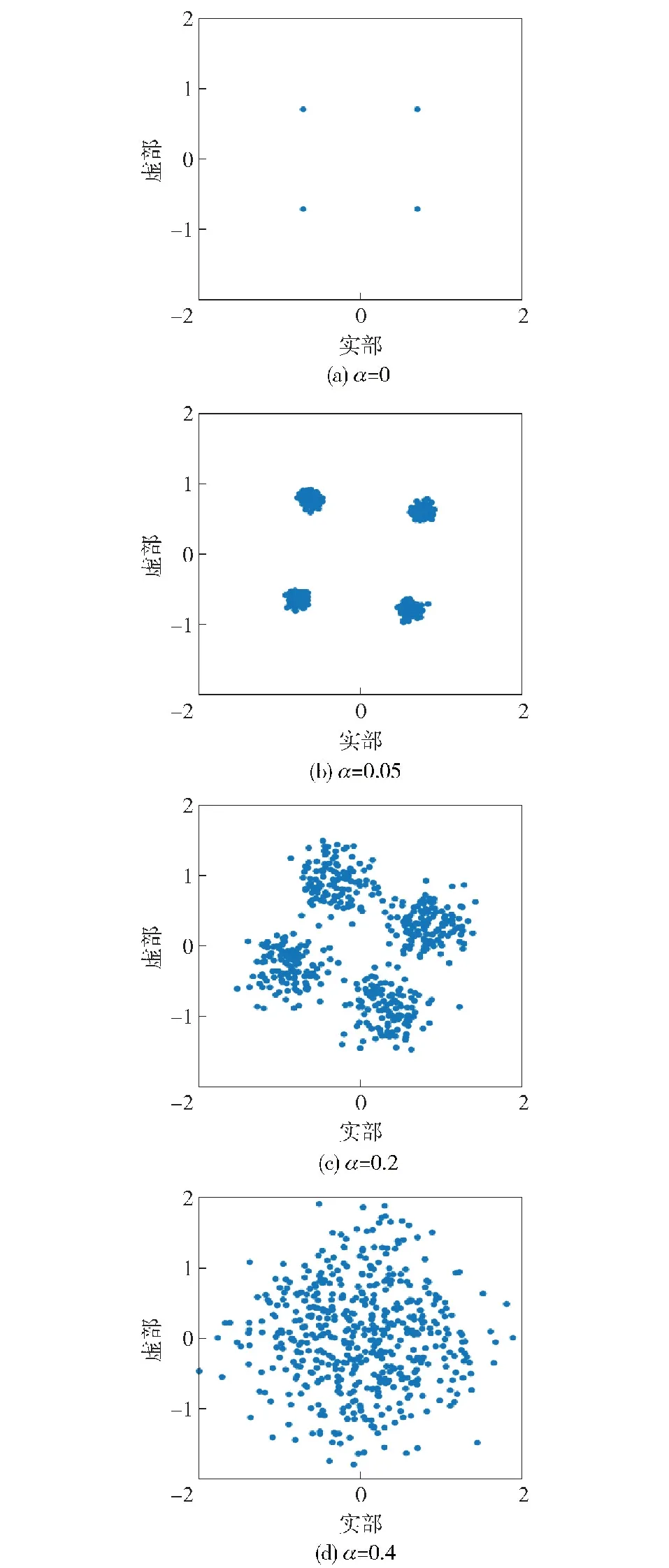
图5 MP-WFRFT信号星座图

从图5中可以看出,QPSK星座图在经过MP-WFRFT后,发生了相位旋转和混淆,并且随着变换阶数α增大,星座图的旋转和混淆程度也伴随着增大,随机分布更加明显。

3.3 DNA动态编码加密性能分析

由于图像相比较传统0-1比特流而言,更加直观、信息更加丰富。因此,利用图像数据进一步分析DNA加密算法对于信息置乱、扩散的效果。

3.3.1 直方图分析

直方图分析反映了明密文的图像灰度分布,均匀分布的密文直方图表明算法能够有效抵抗统计攻击。对图像处理系统中使用的经典图像Lena进行了测试。如图6所示,给出了原始图像以及加密图像数据的直方图,图6(b)可以得出原始数据的大致直方图分布特征,图中的不均匀线表示不规则灰度值信息。同时,对于加密后的情况也给出了图像和直方图,如图6(c)、图6(d)所示。与原始图像相比,加密后的图像没有观察到不规则的图像灰度分布。

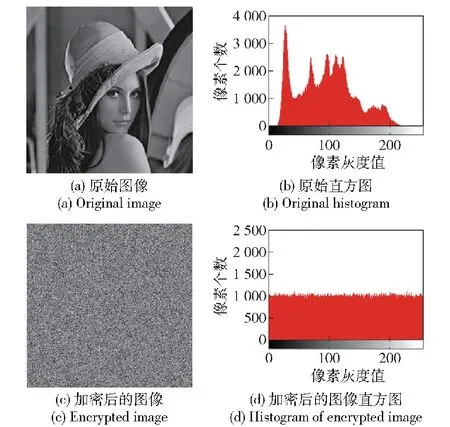
图6 原始图像、直方图和加密后的图像以及直方图

此外,本文演示了非法用户和合法用户的解密图像信息。对于未知密钥的非法用户,不能恢复原始图像数据,并且仅显示不可区分的图像,如图7(a)～图7(c)所示。对于合法的用户,原始图像数据几乎可以完全恢复且没有失真,如图7(d)所示。这些特征表明,本文提出的方案具有较高的加密能力。

图7 非法用户解密和合法用户解密出来的图像

3.3.2 信息熵分析

为了测试DNA动态编码对信息分布的扰乱效果,在图像中进行信息熵分析。熵是测试图像随机性的重要指标,对于8位二进制表示的灰度图像,理想信息熵的值为8,越接近该值,说明图像的加密效果越好。熵的计算公式为

(12)

式中:E(m)为图像m信息熵;N表示每个像素所占的二进制位数;mi表示第i位像素的灰度值,P(mi)表示像素值mi出现的概率。表6展示出了不同普通图像的熵和分别通过不同方案加密后图像的熵,不同尺寸下的最大信息熵以粗体显示。从表6中可以看出,通过本文方案加密的密码图像大多数熵比其他方案的熵更接近8。因此,所提出的方案可以对数据进行高强度加密。

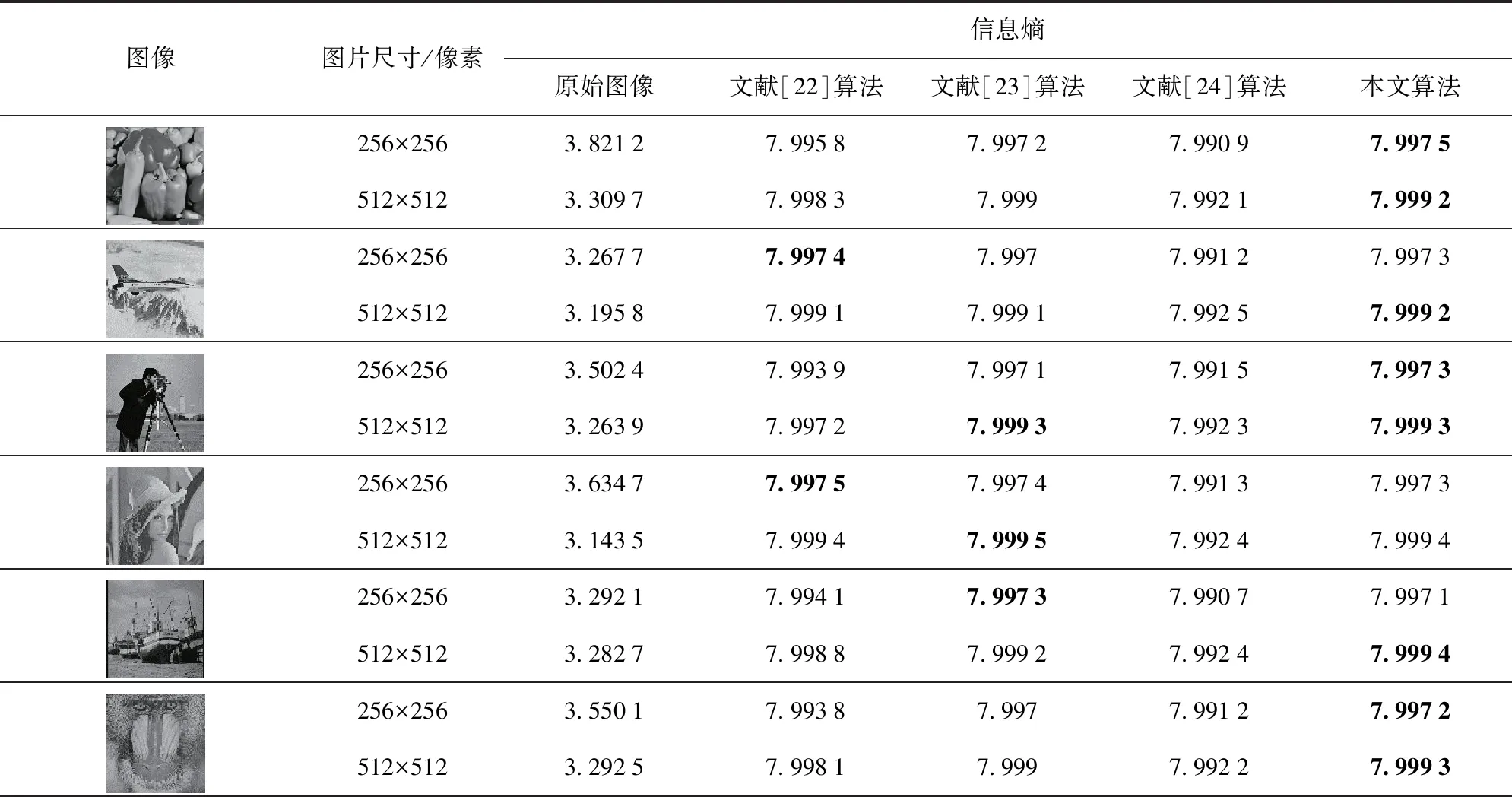
表6 不同方案下普通图像和密码图像的信息熵比较

3.3.3 相关性分析

相关性分析是评价加密算法优劣的重要指标,其主要描述了水平、垂直和斜线3个方向相邻像素点间的相关系数,当密文各个方向上相邻像素值的相关系数越接近于0时,代表加密效果越好。相关系数的计算公式为

(13)

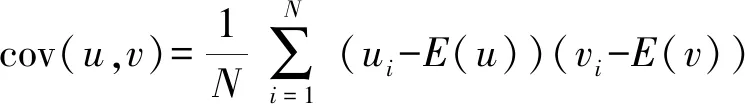
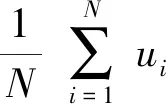
表8对比了文献[25-27]与本文算法下不同密文图像的相关系数,可以看出本文算法具备较好的安全性,能够抵抗统计攻击。

表8 图像相关系数

3.3.4 差分攻击分析

差分攻击分析反映了加密算法对于明文微小变换的敏感程度。通常以像素改变率(NPCR)和一致平均改变密度(UACI)作为衡量加密算法抗差分攻击性能的两个重要指标,计算公式如下:

(14)

(15)

式中:C1、C2为两幅尺寸为W×K的图像;ξ、ψ为图像中像素值的位置索引;D(ξ,ψ)取值满足:

(16)

表9给出了本文加密算法下不同图像的NPCR和UACI值,并与同类文献[25-27] 进行了对比,可以看出本文算法下NPCR和UACI值十分接近理想值99.609 4%和33.463 5%,可抵抗差分攻击。

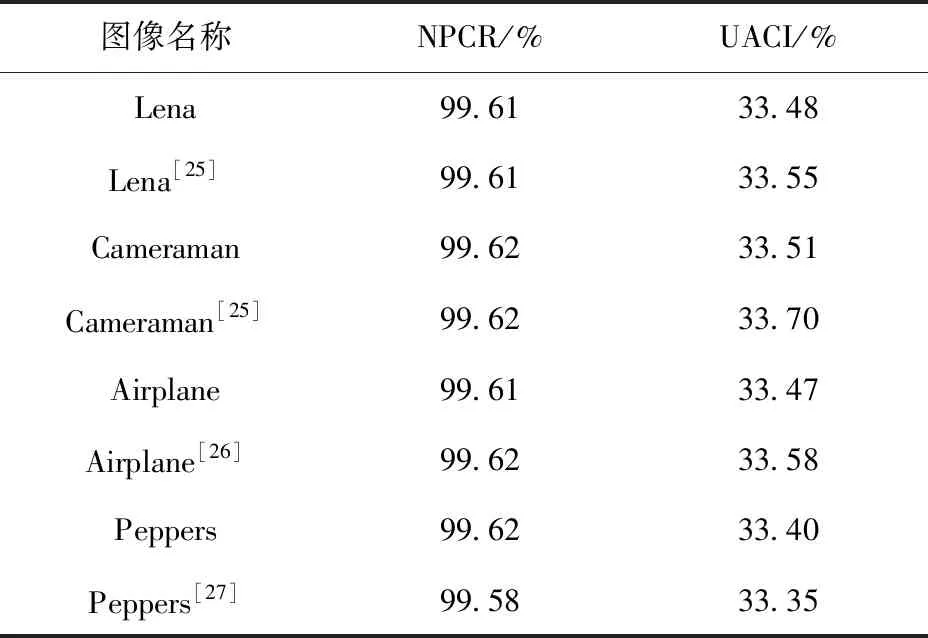
表9 NPCR和UACI

3.4 DNA-VMP-WFRFT信号统计特性分析

信号统计特性分析对于通信信号的抗截获、抗干扰性能十分重要,类高斯分布的信号能够使基于高阶累积量的调制识别方法失效。图8展示了调制阶数α为1时,DNA-VMP-WFRFT信号的复包络、相位统计特性以及信号的同相分量分布情况。图8(a)、图8(b)和图8(c)中的柱形图展示了信号复包络、同相分量以及相位的统计结果,蓝色虚线是与其均值、方差相同的瑞利分布、高斯分布以及均匀分布概率密度曲线。由上述信号统计特性可知:DNA-VMP-WFRFT 信号复包络拟合于瑞利分布,相位分布均匀,且同相分量幅度对高斯分布趋近效果很好,能够实现低概率截获和低概率检测通信的目的。

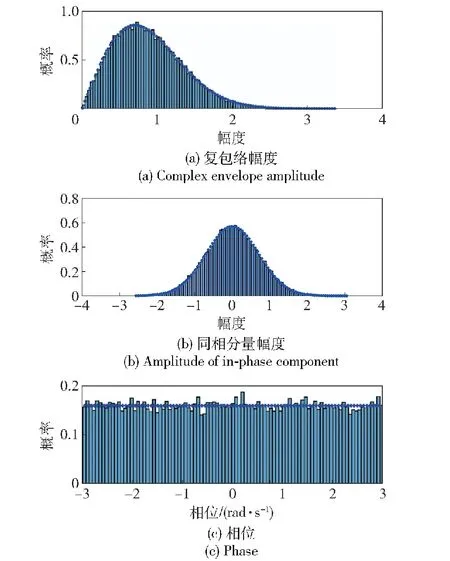
图8 DNA-VMP-WFRFT信号统计特性

3.5 复杂度分析

物理层安全技术在具备高安全性的同时其计算复杂度也应当满足实际应用需求。复杂度分析可以表现出一个算法的运行效率与数据规模间的增长关系,是评估算法性能的重要指标。本文算法的实施过程可分为3个阶段,第1阶段是混沌系统迭代生成伪随机序列,第2阶段利用混沌序列对比特进行DNA加密,第3阶段使用混沌序列对调制信号进行VMP-WFRFT扰动。因此本文的复杂度分析从以上3个阶段进行,假设输入序列长度为N,对各阶段计算次数进行分析统计,结果如表10所示。

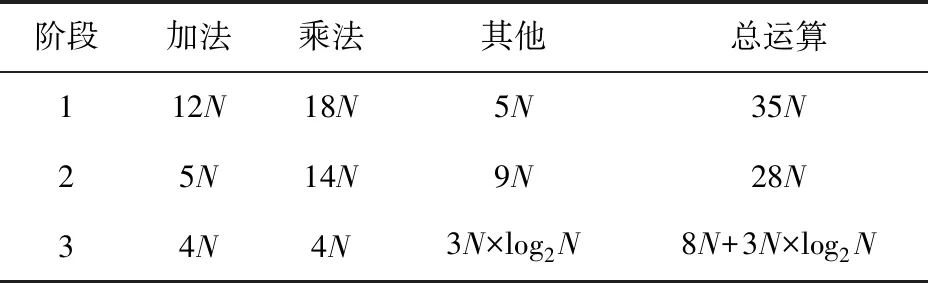
表10 各阶段计算次数

由表10可得本文算法的时间复杂度为O(N×log2N),为进一步与其他混沌加密技术的复杂度进行比较,表11给出了本文算法与文献[28-29]所提加密算法的时间复杂度,可得出本文算法在提升安全传输性能的同时,仍能保持较低的计算开销。

表11 时间复杂度

3.6 误比特率曲线分析

仿真参数如表12所示。

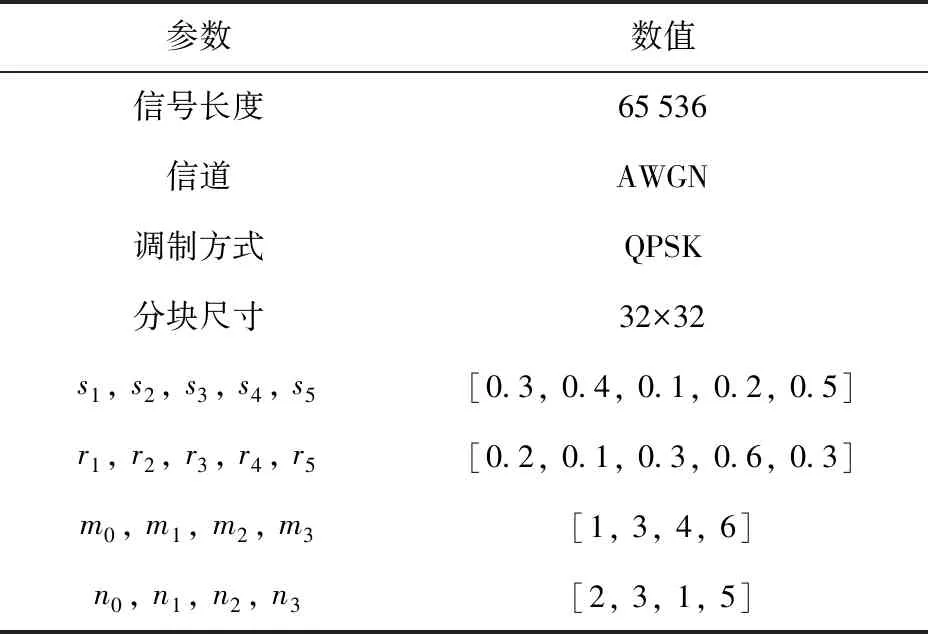
表12 系统仿真参数

误比特率是评价数据通信传输质量重要指标,可以用来衡量加密算法对信号传输所产生的影响。图9所示为经过DNA动态编码和VMP-WFRFT变换后的信号在非法用户接收端与合法用户接收端的误比特率对比。非法用户由于缺少各个阶段的加密密钥,无法正确解调信号,如当尺度向量中存在误差Δm0=0.1、Δn0=0.1或混沌密钥的误差为Δs1=10-15的情况时,误比特率始终维持在0.4～0.5之间。对于合法用户,接收信号性能保持与理论值相近,只产生了较小损耗。密钥空间决定加密算法是否可以抵抗暴力攻击,因此可利用密钥空间评估算法的安全性能,本文算法的密钥为[s1,s2,s3,s4,s5,r1,r2,r3,r4,r5,m0,m1,m2,m3,n0,n1,n2,n3],由于64位双精度数的计算精度为10-15,可得密钥空间大小为(215)18≈1081.2,能够抵抗暴力攻击,说明本文提出的新算法能够显著提高物理层安全传输性能。

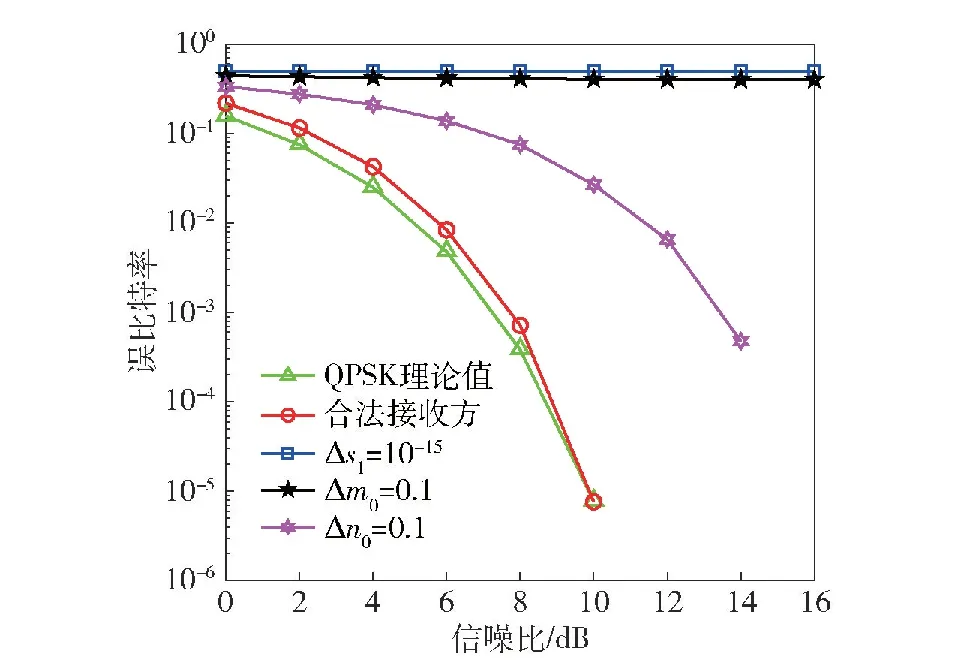
图9 系统误比特率曲线

4 结论

在分析DNA编码和MP-WFRFT机理的基础上,针对DNA编码、运算规则样式少的特点,利用四维低复杂度混沌序列嵌套在DNA动态编码的各阶段中,对比特实施置乱,同时利用混沌序列实现VMP-WFRFT对信号调制样式进行进一步加密,增强MP-WFRFT参数抗扫描特性。综上,本文提出了一种基于DNA动态编码和VMP-WFRFT的安全通信方法。得出以下主要结论:

1)DNA编码加密对于信息的置乱、混淆加密效果较好,在信息熵、相邻像素相关性分析以及差分攻击分析等均有不错表现,VMP-WFRFT能够提高MP-WFRFT参数抗扫描性的同时实现信息的安全传输。

2)该方法计算复杂度低且具备较大的密钥空间,对于合法用户通信质量损耗极低,非法用户在没有正确密钥情况下难以获得有用信息,可以用于解决无线通信中的安全问题。