考虑区间叠加不确定间隙的空间可展机构动力学研究

2023-09-06孟凡斌张渤洋侯月婷王震南

上海航天 2023年4期

孟凡斌，张渤洋，侯月婷，王震南

（1.天津大学精密仪器与光电子工程学院，天津 300070；2.河北工业大学机械工程学院，天津 300401；3.天津航天机电设备研究所天津市微低重力环境模拟技术重点实验室，天津 300301；4.哈尔滨工程大学机电工程学院，黑龙江哈尔滨 150001）

0 引言

空间展开机构［1-2］高精度展开是卫星天线［3］、太阳能列阵［4］等航天部组件稳定运行的前提。但是受设计公差、加工和装配误差，以及部组件运行过程中间隙接触、挤压、摩擦造成的关节变形等［5-6］因素影响，间隙大小呈现区间不确定现象，造成系统动力学特性难以精确预示的问题。在含区间不确定的多体系统动力学建模过程中，将不确定参数［7-9］认定为随机变量与区间变量，是研究含不确定参数多体系统动力学常用方法。其中，将不确定参数认定为随机变量常采用蒙特卡洛方法或者多项式混沌展开逼近方法［10］。由于航天机构场地与成本的限制，无法进行大量试验来补充试验数据库，采用传统的不确定性分析模型对空间展开机构整体进行可靠性分析难以实现。为解决小样本航天机构中认知不确定分析问题，将航天机构中不确定参数进行处理。

针对区间不确定量化［11-12］方法，对代理模型［13］（包括多项式模型）、Kringing 模型以及神经网络［14-17］等进行量化分析，其中通常选取多项式模型为代理模型。WU 等［18］利用泰勒多项式展开与子区间技术相结合的方法与切比雪夫区间方法研究了含区间参数多体系统的响应分析，从而有效避免区间误差叠加导致长时间计算精度不准的问题，降低含区间参数求解中的“过度估计”。邓汉卿［19］针对空间展开索网天线对机构自由度进行分析，通过运动螺旋系提出广义机构的逆运动综合方法，并给出展开天线的测地线索网生成方法。肖剑［20］基于极限状态函数、有限元方法与反向传播（Back Propagation，BP）神经网络，提出针对空间展开绳系的高精度全局代理模型。XIANG 等［21］基于切比雪夫区间求解方法对考虑不确定间隙参数与旋转关节摩擦系数的多体系统进行了灵敏度分析，弥补了预测与测量之间的偏差，提高了机构响应参数变化的灵敏度。MA 等［22］建立了基于实验拟合参数的改进薄层单元（TLEs）方法来模拟界面上接头的动态特性，并基于切比雪夫多项式分析了含区间参数转子系统的时域响应。

然而，上述分析方法在进行不确定性分析时，由于区间参数取不同样本点时，得到的动力学响应出现不同的频率与相位差，且随着时间的增大而逐步扩大，导致瞬时相位累积效应。由此，CUI 等［24］结合不确定分析方法与信号分解，将系统的时域响应分解为若干振动项与趋势项的叠加，并在每一时刻下建立相应代理模型，解决了传统不确定分析长时域信号瞬时相位累积效应。

本文通过对不确定间隙进行描述，结合传统接触模型提出含不确定区间间隙接触模型，并将其嵌入系统动力学模型，通过切比雪夫扩张函数对含不确定区间系统动力学模型进行求解，提出一种相适应的局部均值分解方法、瞬时叠加方法与区间扩张方法进行区间叠加处理，揭示系统区间累加下动力学响应边界分布规律。

1 不确定间隙描述

在传统含间隙多体系统动力学分析过程中，普遍将间隙认定为旋转关节孔半径与轴半径的相减，推导过程基于初始最大间隙所得。在展开机构运转过程中，由于多间隙的耦合作用，针对旋转关节间隙处发生接触碰撞-碰撞分离-再次碰撞的运动过程中的碰撞分离过程，旋转关节产生碰撞分离过程并不是每次都可以到达初始间隙最大值再次发生下次碰撞，如图1 所示。每一次发生接触碰撞的初始间隙是一个不确定量，其不确定长度可以表示为

图1 旋转关节轴心任意时刻位置Fig.1 Diagram of the position of the axis of the rotary joint at any moment

式中：ΔRx为旋转关节初始间隙不确定量横向投影距离；ΔRy为旋转关节初始间隙不确定量纵向投影距离。

将旋转关节间隙与相连接的连杆长度简化为开环机械臂两段，利用欧氏运动群上的卷积探究开环机械臂的运动传播问题，给出两端机械臂运动工作空间密度为ρ1(g)与ρ2(g)，g=(R，x)∈SE(n)，对这2 个工作空间密度进行卷积，得到整体机械臂运动范围密度为

式中：SO(n)为机械臂横向运动区域量，R为全域量。

在旋转关节运转空间环境中，假设间隙角θ在运转角度[0，2π]内均匀分布：

间隙角θ在X方向累计分布函数可以表示为

同理，间隙角θ在Y方向累计分布函数可以表示为

对间隙角在X与Y方向上的累计分布函数分别求导，可得间隙角在X与Y方向上的概率密度函数ρx与ρy：

利用欧氏运动群上的卷积公式对式（6）与式（7）间隙角概率密度函数进行卷积积分，可得间隙角末端点在间隙圆内分布概率密度函数为

根据卷积在Rn的性质，可以得到

结合式（9）与式（10），间隙角末端点分布概率密度函数均值μ与σ可表示为

式中：Qn为n×n的单位矩阵。

对于运动范围不受限制的旋转关节，其间隙角末端点分布可能为间隙圆内任意一点，根据中心极限定理与迭代关系，利用高斯概率函数构建间隙角末端点在X方向与Y方向分布概率密度函数：

结合式（13）与式（14）间隙角末端点在X方向与Y方向分布概率密度函数，可得间隙角末端点全域联合分布概率密度函数为

在不考虑嵌入量的情况下，间隙角末端点分布最大值为间隙圆边界ΔR，因此在考虑机构运动行程与分布区间大小，给出间隙角末端点在间隙圆概率分布密度函数：

2 含不确定机构动力学建模

在考虑实际接触过程中，随着空间展开机构多单元的叠加特点，导致不同位置处的间隙为一未知量。通过对不同位置处间隙采用区间变量的形式进行统一描述，对空间展开机构进行高精度建模分析。

根据Winkler 弹性基础模型［25］，接触体在接触位置产生一定变形，如图2 所示，接触区域径向位移与最大法向穿透深度的关系满足刚性接触体的几何边界条件，其变形量可表示为

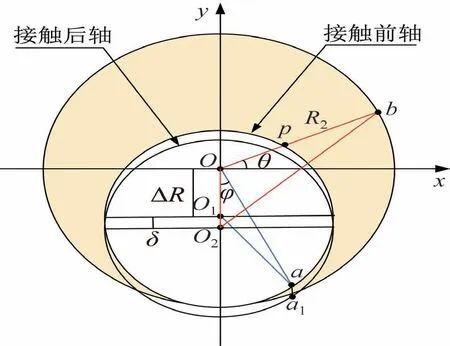
图2 接触体二维接触模型Fig.2 Two-dimensional contact model for contact bodies

式中：R1、R2分别为接触体半径；ΔR为初始间隙；φ为半接触角度。

轴孔接触模型半接触角度φ处的法向接触应力为

式中：E为接触体弹性模量；c为接触区域弹性层厚度。

在接触区域上任取一弹性微元，对式（18）在半接触区域内进行积分，r由于轴孔初始间隙ΔR和轴孔嵌入量δ均远小于轴半径R1，接触点与固定坐标系原点之间的距离近似于接触体半径R1。则接触区域承受的接触力为

将式（17）代入式（19），忽略高阶项，接触域单位接触长度接触力为

结合图1 旋转关节在发生三接触状态的过程中，其每一次碰撞点初始位置都不尽相同，导致接触体瞬时接触力产生差异。其考虑不确定区间间隙的接触力模型可进一步表示为

式中：[ΔR]为不确定初始间隙值，结合式（16）可表示为[R]=R2-R1-|f(x)|。

采用拉格朗日方程对空间展开机构进行动力学建模，空间展开机构展开单元动力学方程可表示为

式中：L为拉格朗日函数，定义为空间展开单元动能与势能的差值；φi为广义坐标；Fi为广义坐标对应的广义力；[Fc]为接触体的接触力。

3 考虑不确定参数切比雪夫求解方法

切比雪夫区间分析方法作为应用最为广泛的非嵌入式多体系统动力学解算分析方法，采用切比雪夫函数进行区间求解，不仅在计算含区间不确定的多体系统动力学方程时有较高的计算精度，而且其扩张函数对考虑不确定间隙导致系统动力学方程维度增加时，区间计算产生的累加效应能够起到一定的抑制作用，可以用作较长时间分析含区间不确定的多体系统动力学响应特性。

3.1 切比雪夫扩张函数

基于Weierstrass 理论，在定义区间[a，b]上连续函数采用多项式的形式逼近，对于一维问题，在定义区间[a，b]上的p阶切比雪夫级数为

式中：变量x∈[a，b]且θ∈[0，π]。

对于一维单变量连续函数f(x)∈[a，b]可用切比雪夫扩张函数近似表示为

式中：fi为多项式的系数。

将每一个一维多项式表示为张量积，从而给出n维切比雪夫多项式定义为

多元函数f(x1，x2，…，x n)用n次切比雪夫多项式近似可表示为

式中：fj1，j2，…，jk为n次多元函数的系数，基于Mehler 积分可知

式中：m为多项式插值点数，一般取m=p+1 可保证近似精度。

综上所述，含区间不确定性的空间展开机构动力学方程，可通过切比雪夫多项式的形式，构建响应函数的代理模型，并采用区间计算的方法计算系统动力学方程的区间解。

3.2 切比雪夫扩张函数求解方法

本节针对多体系统动力学模型，提出切比雪夫扩张函数对动力学模型进行求解，通过切比雪夫正交多项式构建代理模型，完成对动力学模型求解，切比雪夫求解流程如图3 所示。

图3 切比雪夫求解动力学方程流程Fig.3 Flow chart of Chebyshev dynamic equation solving

在图3 中，n为含区间间隙空间展开单元动力学方程维数，y0为动力学响应初始值，t0为初始时间，tend为结束时间；h为切比雪夫区间求解的迭代步长；k为切比雪夫多项式阶数。

采用切比雪夫多项式构建含区间间隙空间展开单元动力学方程代理模型时，将具有含不确定区间参数的空间展开单元动力学方程，转换为仅具有特定区间参数的动力学方程并进行求解，根据多个所求数值解构造切比雪夫代理模型，基于区间算法来计算含不确定区间参数的空间，展开机构动力学方程的区间解。其区间解可用如下形式表示：

式中：yj+1为tj+1时刻含不确定区间参数的空间展开单元动力学方程数值解；y(tj)为tj时刻插值点处含不确定区间参数的空间展开单元动力学方程数值解。

4 小区间叠加方法

针对区间求解方法中区间叠加误差过大问题、分解的小区间整合成大区间的问题与启动阶段估计不准问题，提出局部均值分解方法、瞬时叠加方法与区间扩张方法，为提高切比雪夫求解精度大区间分解的小区间整合成大区间下的区间边界，并再此基础上降低启动阶段估计精度。通过小区间累加方法在切比雪夫求解方法上进行进一步处理，获得较高精度区间边界值。

4.1 局部均值分解方法

针对切比雪夫区间求解方法区间叠加导致误差累积效应，在长时域内求解仅保持短时间有效的缺点，对切比雪夫求解获得动力学响应边界(ω，t)采用局部均值分解的方法，将响应边界分解为若干个响应幅值与响应相位乘积之和的形式，对动力学响应边界(ω，t)中响应幅值a(ω，t)与响应相位φ(ω，t)建立代理模型，解决传切比雪夫区间求解方法相位累计效应问题。其中响应幅值通常是缓变甚至单调的信号，响应相位指幅值为1 的函数，代理模型指计算结果与原模型非常接近，并便于求解的模型。

具体步骤如下：取初始残差函数ri(t)等于初始动力学响应边界(ω，t)，提取初始动力学响应边界中的极大值点ai与极小值点bi，对提取的所有极大值点ai进行局部均值拟合，得到上包络线vi(t)；同理，得到下包络线ui(t)，将上包络线vi(t)与下包络线ui(t)进行瞬时均值处理，得到动力学响应边界瞬时均值ci(t)为

动力学响应瞬时幅值函数在时域内累加可表示为

动力学响应瞬时相位函数在时域内累加可表示为

对初始信号全部采样点处理完成后，φi(t)在时域内累加构建为动力学区间响应相位ψi(t)，ci(t)时域内累加构建为动力学区间响应幅值Ci(t)，将动力学区间响应幅值函数与动力学区间响应相位函数相乘，可得第i阶乘积函数动力学区间响应代理模型PFi(t)：

新的残差函数ri(t)可表示为

综上所述，通过局部均值分解方法，将动力学区间响应边界分解为动力学响应幅值函数与动力学响应相位函数乘积之和的形式，具体表达形式为

4.2 瞬时叠加方法

基于上节提出的局部均值分解方法，结合传统响应面分析方法，提出多体系统动力学瞬时叠加方法，对切比雪夫区间求解过程中大区间分解后的小区间进行叠加，获得初始区间下系统动力学响应边界，具体可分为以下步骤。

1）输入动力学响应边界、不确定间隙[r]，在不确定间隙[r]中选取n个样本，记作：r1，r2，…，rn，n为样本序号，n个不确定参数对各样本对应的时域内响应分别为x(r1，t)，x(r2，t)，…，x(rn，t)。

2）采用4.1 节提到的局部均值分解方法，将时域内的不确定参数样本响应分解为n个动力学响应幅值函数与动力学响应相位函数乘积之和与相对应的残差函数。其中分解结果如下：

3）在每一时刻下，基于多项式函数拟合建立切比雪夫区间求解响应的瞬时响应幅值函数与瞬时响应相位函数，以及残差函数的代理模型，得到相应代理模型，分别逼近真实解。

4）计算每一时刻下，动力学响应边界分解的瞬时响应幅值函数代理模型与瞬时响应相位函数代理模型的耦合形式

5）在耦合形式代理模型中加入残差函数代理模型，计算完成形式的代理模型，得到完全的谐波叠加形式的代理模型为

6）计算代理模型上边界与下边界。如图4所示。

图4 瞬时叠加方法流程Fig.4 Flow chart of the instantaneous superposition method

4.3 区间延拓方法

在切比雪夫区间求解过程中，在启动阶段出现区间求解误差较大问题，启动阶段前没有相对应的区间与启动阶段进行关联，单一区间求解状态下容易出现误差较大的情况。启动阶段以前，区间通过余弦拓展方法进行扩张，在求解过程中启动阶段有2 个甚至多个区间联合求解，解决启动阶段区间误差较大问题。

通过切比雪夫区间求解获得系统动力学响应边界以后，可以根据零点附近动力学响应变化趋势，在动力学响应零点以前区间增加相应的相位、幅值与频率适当的余弦延拓函数，使动力学响应区间代理模型可以在零点处有更多区间与相应响应边界函数，从而提高启动阶段所得上下包络线精度，余弦延拓函数及参数定义如下：

式中：ci(t)为代理模型瞬时幅值函数；φi(t)为代理模型瞬时相位函数；ri为代理模型误差；Ti为延拓周期数，在数值上等于延拓周期与相邻极大值与极小值之前时间差的n倍。

通过上述余弦延拓方法，可保证代理模型在展开过程任意有效时域内都有相邻区间关联求解，从而降低启动过程中单一区间求解带来的动力学响应区间边界误差。

5 系统区间累加动力学响应边界分析

以平板式合成孔径雷达（Synthetic Aperture Radar，SAR）天线展开机构为研究对象，如图5 所示，通过区间求解来分析区间间隙对空间展开天线展开过程的动力学特性影响，选取区间间隙大小为［0.01，0.1］ mm，连杆刚度系数为5×105N/m，动摩擦系数为0.1。

图5 空间展开机构仿真Fig.5 Simulation schematic of the spatial unfolding mechanism

多体系统动力学特性边界计算流程如图6 所示。对多体系统旋转关节间隙进行不确定参数量化取值，将所得区间值代入区间接触模型进行计算并嵌入到含不确定间隙多体系统动力学模型，通过切比雪夫扩张函数进行求解，并对所得结果通过小区间叠加的区间处理方法进行处理，得到动力学特性边界。

图6 多体系统动力学特性边界计算流程Fig.6 Flow chart of the dynamics boundary calculation for multi-body system

［0.06，0.1］ mm 区间间隙标记点小区间叠加区间结果与切比雪夫区间计算对比如图7 所示。对区间计算结果进行区间划分，并统计每个区间下概率密度，同时由区间计算给出该间隙下标记点误差分布区间。采用小区间叠加方法可明显降低区间边界处由代理模型长时域区间迭代产生的误差累计效应。将区间叠加计算平均结果与传统拟合结果进行对比如图8 所示，由图8 可知在［0.06，0.1］ mm间隙下区间叠加计算平均结果与传统拟合结果相比提高7.74%，［0.03，0.06］ mm 区间叠加计算平均结果与传统拟合结果相比提高3.73%，可进一步提高空间可展机构展开预示精度。

图7 ［0.06，0.1］ mm 区间间隙标记点区间结果与区间计算结果对比Fig.7 Comparison of the interval results of the marked gap points with interval calculation results in the［0.06，0.1］ mm interval

采用局部瞬时分解方法、瞬时叠加方法与区间扩张方法对不同区间间隙大小与数量下区间边界进行处理，得到大区间下位移偏差区间分布状况，如图9 和图10 所示。

图9 不同间隙大小下叠加区间边界Fig.9 Boundaries of the stacking intervals with different gap sizes

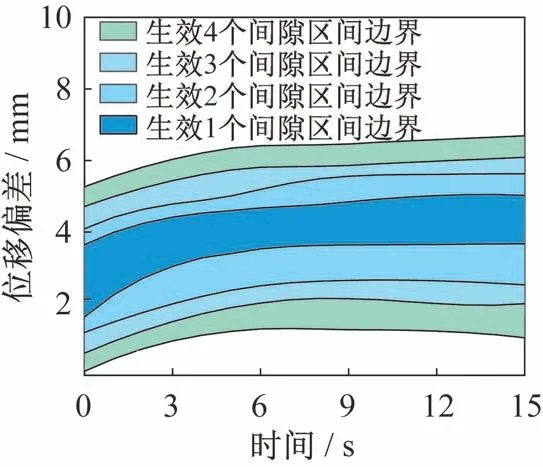
图10 不同区间间隙数量下叠加区间边界Fig.10 Boundaries of the stacking intervals with different gap numbers

由图9 可知，随着间隙区间的增大，系统位移偏差基准值出现逐渐增大的趋势，但是区间范围扩张并不明显。由图10 可知，小区间叠加方法可以有效解决小区间与大区间之间的转换、区间累加效应与边界估计不准的问题。随着生效区间间隙数量的增多，系统位移偏差基准值趋于稳定，但是区间范围产生明显增大。说明间隙大小对系统运动精度产生较大影响，而间隙数量对系统运动稳定度影响较为严重，在对空间展开机构展开过程分析中间隙对系统的影响时，不仅要合理控制各旋转关节间隙大小，同时还要关注由于多级机构叠加从而导致系统间隙数量倍增的状况。