线性调频激光回馈粒度探测灵敏度提升方法*

寇科 王错 王晛 连天虹 焦明星 樊毓臻

(西安理工大学机械与精密仪器工程学院,西安 710048)

激光回馈(或激光自混合干涉)技术在位移、距离、速度、振动等传统物理量测量领域具有广泛的研究和应用.近20 年来,这项技术在纳米粒度检测中也展示出了巨大的前景,其测量原理是: 基于激光束与照射区域每个粒子相互作用的非相干叠加,粒子直径可以通过激光回馈信号功率谱的洛伦兹拟合而求出.激光回馈粒度检测一般使用恒流驱动的半导体激光器,其信号功率谱峰会位于零频附近,只呈现出右侧部分,有些使用固体激光器的粒度传感器通过一对声光调制器进行移频,将功率谱峰搬离零频位置,但是极大地增加了系统的复杂度和费用.本文用线性调制电流驱动半导体激光器,以产生近似线性调频,从而方便地把功率谱峰搬移到任意期望的频谱位置上.此外,适当的光反馈强度下,倾斜的回馈信号条纹会导致功率谱峰产生高次谐波,这些谐波峰的频谱展宽较主峰更为明显,可以有效提高纳米粒子检测的灵敏度.本文所提出的新技术方案通过数值仿真和实验验证,有望应用在低成本、结构紧凑、高灵敏度的激光回馈粒度传感器或相关仪器中.

1 引言

凭借着易于准直、结构简单紧凑、低成本、高灵敏度和不依赖激光器类型的优点[1−4],激光回馈(或激光自混合干涉)技术吸引了世界各地研究者的注意,且在传统物理量(如位移[5]、距离[6]、速度[7]、振动[8]、角度[9]等)测量领域具有广泛的应用.此外,该项技术逐渐应用于纳米粒度检测中,这主要依赖于腔内光场与悬浮在静态液体或动态液流中的粒子的后向散射光场的相互混合.

近20 年来,许多国内外研究者开展了激光回馈纳米粒度检测的相关研究工作,并取得了丰硕的成果.2005 年,Zakian 等[10]最早将激光回馈技术应用于粒径测量,他们基于速率方程推导了激光散射回馈下光场所满足的规律,指出自混合功率信号频谱可以用洛伦兹函数拟合,对水中20—200 nm范围内的5 种聚苯乙烯微球进行测量,得出粒径越小自混合信号频带越宽的结论,并对频带宽度和粒径作了指数拟合,最高实现了3%左右的粒径测量精度.同年,Otsuka 等[11]基于载波频分多路复用技术,用一个微片固态激光器同时独立测量两个样品池中布朗粒子的运动,并通过光子相关光谱法得到粒径分布柱形图,粒径测量精度为5%.2006 年,Sudo 等[12]使用微片固态激光器检测纳米粒子,通过两个声光调制器进行上下变频将信号功率谱搬离原点,测量水中262 nm 的聚苯乙烯微球,粒径测量精度在5%左右.同年,他们通过测量微球得到粒子直径、浓度与信号功率谱的对应关系,并指出多粒径混合溶液的功率谱拟合线可看作各粒径溶液功率谱所拟合洛伦兹曲线的线性叠加,该研究为本项目中的多通道检测方案提供了启发[13].2007 年,Sudo 等[14]采用同样的装置测量流体通道中的粒子浓度,指出溶液按一定方向流动时信号功率谱呈现非对称性,并对262 nm 的聚苯乙烯微球和3 µm 的红细胞分别实现了质量分数为10–6和10–5的探测极限.2008 年,王华睿和沈建琪[15]基于激光回馈技术,采用超平面投影法求得多粒径混合溶液中的粒径分布,粒径测量精度为5%—10%;2010—2012 年,他们基于高斯光场分布和时延速率方程推导得出了流动和静止溶液中粒子回馈信号功率谱密度的解析表达式,并通过数值仿真分析了功率谱密度的相关特性[16,17];2013 年,他们设计了16 通道模拟电路分析激光回馈信号,以纯硬件方式实现了粒径分布的快速测量,克服了超平面投影法运算耗时的问题[18].2016 年,Contreras 等[19]通过乙炔气室边缘滤波器将激光回馈频率信号映射为功率信号来探测气流中的微粒,提高了信噪比,把探测距离扩大到10 m.2017 年,Ramírez-Miquet 等[20]对激光回馈流速测量做了综述,基于速率方程推导了流体粒子散射下回馈信号的变化规律,并指出该技术在粒度和流速测量中的潜在应用.同年,法国的Moreira 和国内的赵宇等[21]通过半导体激光器的回馈效应探测到了流体中远小于激光半波长的单个粒子并测得其速度.2018 年,Herbert 等[22]基于激光回馈技术对混合流体中不同大小的粒子进行了区分.2019 年,赵宇等[23]开始将激光回馈技术应用于微流体研究之中,分析了粒子大小、浓度、通道表面折射率、通道尺寸对回馈信号频谱的影响,随后他们又使用希尔伯特变换方法对微流道中的粒子大小展开了测量,对于微米量级的粒子实现了300 nm 的分辨率[24].上述研究现状涉及了纳米粒度检测的多个方面,但并未针对检测灵敏度开展相关研究.

为进一步提高粒度检测灵敏度,并减小系统硬件复杂度,本文通过半导体激光器中注入电流与激光频率的近似线性关系将功率谱峰从零频处搬移到任意频谱位置,同时在适当的光反馈强度下,功率谱峰的高次谐波会伴随着激光回馈信号条纹的倾斜而产生,这些高次谐波峰会呈现出比主峰更为显著的频谱展宽,从而有助于提高粒度检测的灵敏度.该方案有望应用于开发低成本、结构紧凑、高灵敏度的激光回馈粒度传感器或相关仪器.

本文结构如下: 第2 节简要介绍激光回馈粒度检测的理论背景和相关公式;第3 节基于Python语言进行数值分析并给出仿真结果;第4 节给出实验结构图、实验条件和相关实验结果,并与仿真结果对比,同时进行简要分析;第5 节总结,并指出所提方案的潜在应用场合及后续研究计划.

2 线性调频激光回馈纳米粒度检测原理

2.1 激光回馈纳米粒度检测原理

激光回馈纳米粒度检测的基本公式如下:

其中,S表示激光回馈信号的功率谱, 〈N〉 表示激光照射区域的平均粒子数目,ω表示激光回馈信号的角频率,ω0表示功率谱种洛伦兹峰搬移的中心频率,D为扩散系数,q为散射矢量,n为溶剂的折射率,λ为激光波长,θ为散射角(在激光回馈结构中,θ=π).根据斯托克斯-爱因斯坦关系式,散射系数D与粒子直径x的关系可以表示为

式中,kB为玻尔兹曼常数,T为热力学温度(开氏温度),η为溶剂的黏度,x为粒子直径.黏度η和温度T的经验关系式如下:

其 中,A=2.414×10-5Pa·s,B=247.8 K,C=140 K.在室温(25 ℃,298 K)下,纯水的黏度大约为 8 .935×10-4Pa·s.在采集到激光回馈信号并求得其功率谱之后,可以通过洛伦兹拟合直接求解谱峰宽度Dq2,进而计算出粒径x.

2.2 线性调频激光回馈工作原理

根据经典的三镜法-珀腔模型和时延速率方程模型,激光回馈功率和频率变化的方程如下:

其中,P0和ϕ0分别表示无光反馈时激光器的功率和相位;ϕF为有光反馈时的相位;m一般看作调制系数;α为激光器的线宽展宽因子.C为光反馈强度系数,其表达式如下:

其中,L是激光器出射端面到反射物体的绝对距离,n和l分别为增益介质折射率及内腔长度,R2和R3分别为激光器出射端面和外部反射体的功率反射率.在被测物体距离及激光器都确定的情况下,外部反射率R3成为了决定光反馈强度的关键参数.

在注入电流调制和弱反馈的条件(C＜1)下,激光频率随着注入电流近似线性变化,则有反馈相位ϕF可以表示为(8)式,功率方程(5)中的关键波动项可表示为(9)式.

其中,c为光速;ν0为无光反馈时的激光频率;L表示被测样品与激光器出射端面之间的距离;W(t)表示调制电流波形,为了实现线性调频,一般选择锯齿波或三角波;γ为频率调制系数,单位为Hz/mA;这属于半导体激光器的内在特性,对于一个具体的激光器而言,该参数可以看作常数.正如在线性调频激光回馈测距中那样,频移量fs可以表示为

对于一款已确定的半导体激光器而言,频移量与被测样品距离和调制电流斜率直接相关联.通过这种线性调频的方式,零频处只显示一半的功率谱峰就会被搬移到频率fs处,且该频率可以很便捷地由距离L及调制波形W(t)的参数来进行调整.

3 仿真分析

基于Python 语言,结合Numpy 和Scipy 包开展数值仿真分析,并通过Matplotlib 包绘制仿真结果图.图1 为线性电流调制下仿真激光回馈信号生成的原理图.首先,设置一个随机运动的粒子,根据粒子运动位移与调制三角波电流引起的线性频率变化生成无反馈状态下的初始相位φ0,然后参照文献[25]中提出的激光回馈信号生成方法,通过相位插值得到归一化的回馈信号,接着更换下一个随机运动的粒子,继续执行上一步操作,直到为所有粒子都生成相应的激光回馈信号,最后将所有粒子对应的激光回馈信号进行平均,即得到最终的激光照射区域内所有粒子的整体激光回馈信号.由于对激光器注入电流进行了三角波线性调制,激光回馈信号中必定包含了幅度调制的不利影响,通过相减操作去除调幅影响之后才可以进行后续分析.

图1 仿真信号生成原理图Fig.1.Schematic diagram of the simulated signal generation.

在进行多粒子体系的仿真分析之前,首先对单个粒子线性运动产生的激光回馈信号及其功率谱进行了简单的数值仿真,结果如图2 所示.单个粒子线性运动,其激光回馈信号表现为多普勒频移信号,随着光反馈强度增加,信号条纹倾斜程度逐渐增加,高次谐波逐渐出现在功率谱图中.接着开始进行多粒子体系的仿真分析,采用的仿真参数数值或其范围见表1.

根据上述仿真信号生成原理,将多个不同速度的小片段线性运动连接成随机运动,再将每个粒子随机运动的激光回馈信号叠加,去除调幅影响之后的归一化激光回馈信号示例如图3 所示.纳米粒子在溶液中做随机布朗运动,其激光回馈信号时域波形必然呈现出杂乱无章的状态,粒径信息难以从时域波形中分析得出.在4 种不同的光反馈强度水平下,对激光回馈信号进行频谱分析,得到的归一化功率谱图如图4 所示.仿真中未人为添加噪声,去除三角波调幅影响之后的残留构成了噪声本底.谐波阶次通过箭头标记指出.在较弱光反馈强度水平(C=0.1)下,功率谱图中仅清晰地呈现出了从零频位置搬移的洛伦兹峰,其二次谐波峰几乎淹没于噪声中,勉强可见.随着光反馈强度水平的不断提高,高次谐波峰逐渐呈现,谐波阶次越高,谱峰越接近本底噪声,信噪比越低,但是谱峰的宽度越宽.由(1)式—(3)式可知,谱峰的宽度直接对应着纳米粒子的粒度,加宽之后的谱峰可以更为灵敏地识别出粒度变化.在未被噪声淹没的前提下,灵敏度的提升倍数完全取决于谐波峰的阶次,即N次谐波的检测灵敏度会提升N倍.

图4 不同光反馈强度下激光回馈仿真信号功率谱图Fig.4.Power spectra of laser feedback signals at different feedback strength levels.

以光反馈强度C=0.7 为例进行分析,得到拟合宽度参数Dq2与谐波阶次的关系如表2 所列.表2 中每个谱峰宽度数据均是10 次洛伦兹拟合结果的平均值,该结果表明,随着谐波阶次增加,谱峰宽度几乎成比例展宽,这相当于将粒度变化引起的谱峰宽度变化进行了成比例放大.通过高次谐波峰来进行粒度分析可以成倍地提高纳米粒度检测的灵敏度,N次谐波峰的检测灵敏度将会提升N倍.但是,随着谐波阶次升高,谱峰会更加接近噪声本底,信噪比随之下降.实际检测工作需要在谐波阶次和信噪比之间作出折衷.

表2 不同谐波阶次下洛伦兹峰的宽度Table 2.Width of Lorentz peak under different harmonic orders.

4 实验测试

本文也开展了相应的实验测试工作,实验系统示意图如图5 所示.实验用悬浮于蒸馏去离子水中的聚苯乙烯微球作为被测对象,混合物的质量分数设置为0.1%以消除多重散射的影响.实验光源为半导体激光器L850 P010 (索雷博,美国),出射光波长为850 nm,最小阈值电流为10 mA,最大输出功率为10 mW,且其内部封装了一个用于功率监测的光电二极管.激光器安装于温控底座LDM9T(索雷博,美国)中,其温度控制稳定性优于0.02 ℃.激光器驱动电源为LDC201CU (索雷博,美国),其驱动电流噪声小于0.2 µA.当激光回馈现象发生时,光电二极管产生的光电流送入自制信号调理电路,该电路中包含了跨阻放大和带通滤波单元.放大和去噪后的激光回馈信号通过数据采集卡USB61902 (简仪科技,中国) 采集到计算机中进行后续数据分析.

图5 实验结构示意图Fig.5.Schematic diagram of the experimental setup.

实验中采用与仿真几乎一致的参数,不同之处在于,测试系统的光反馈强度无法精确量化调控,照射区域中的粒子数目无法精确得知,除了去除调幅影响的残留之外,各类噪声干扰(包括激光器、光电二极管、信号调理电路的噪声等)更多.以标称粒径为200 nm 的聚苯乙烯微球溶液为例,所测得的激光回馈信号功率谱如图6 所示.实验采集的信号与仿真信号一样,均呈现为杂乱无章的状态,无法从时域信号中分析出有效消息,故时域波形不再展示.实验中溶液浓度低,光反馈强度偏弱,功率谱图中仅可以较为清晰地看到从零频处搬移的洛伦兹峰及其二次谐波.红色曲线为洛伦兹拟合结果,图中可以很直观地看到二次谐波峰的宽度大于主峰宽度.

图6 激光回馈实验信号功率谱示例Fig.6.Exemplary power spectrum of laser feedback signal in experiments.

实验中在待测样品之前插入中性滤光片以进一步降低光反馈强度,这时所得的激光回馈信号功率谱如图7 所示.图7 中二次谐波峰难以辨识,这种现象足以证明,高次谐波峰的出现源自于光反馈强度增加所带来的信号条纹倾斜程度的增加.

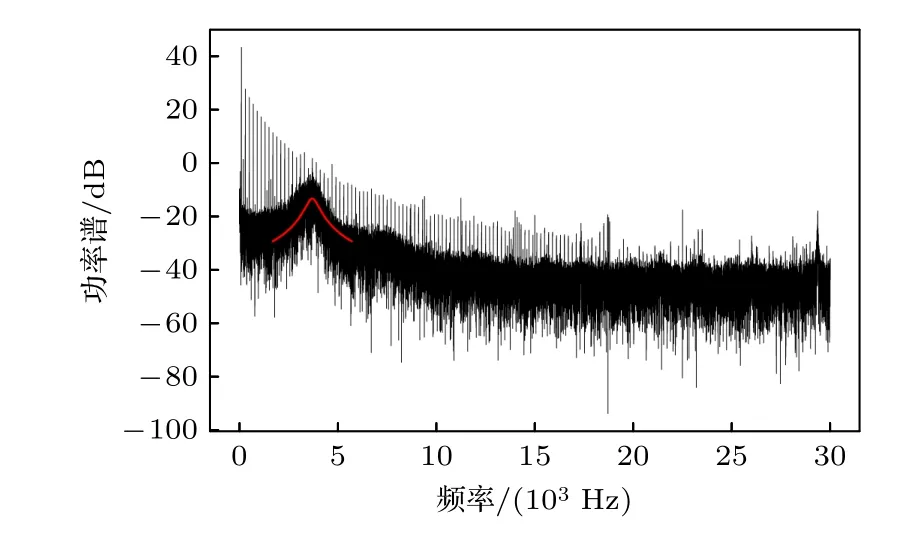
图7 添加滤光片之后激光回馈实验信号功率谱示例Fig.7.Exemplary power spectrum of laser feedback signal in experiments after optical filter inserted.

为了验证线性调频引起的高次谐波宽度被成比例展宽,选取了多种不同粒径的聚苯乙烯微球作为被测对象,取消滤光片,对每种微球产生的激光回馈信号,按照时间分割出100 段分别进行频谱分析和洛伦兹拟合,求得基频峰和二次谐波峰宽度的平均值与标准差,分析结果如图8 所示.可以看出,对于多种不同粒径的粒子,二次谐波的峰宽几乎均为对应主谱峰宽度的两倍,这与仿真分析结果相符合.随着粒径的增大,布朗运动速度会相应减慢,谱峰宽度逐渐减小,这与现有文献[10,13,15]报道的实验现象一致.通过二次谐波峰进行粒度检测的灵敏度将会提升为主峰的2 倍.

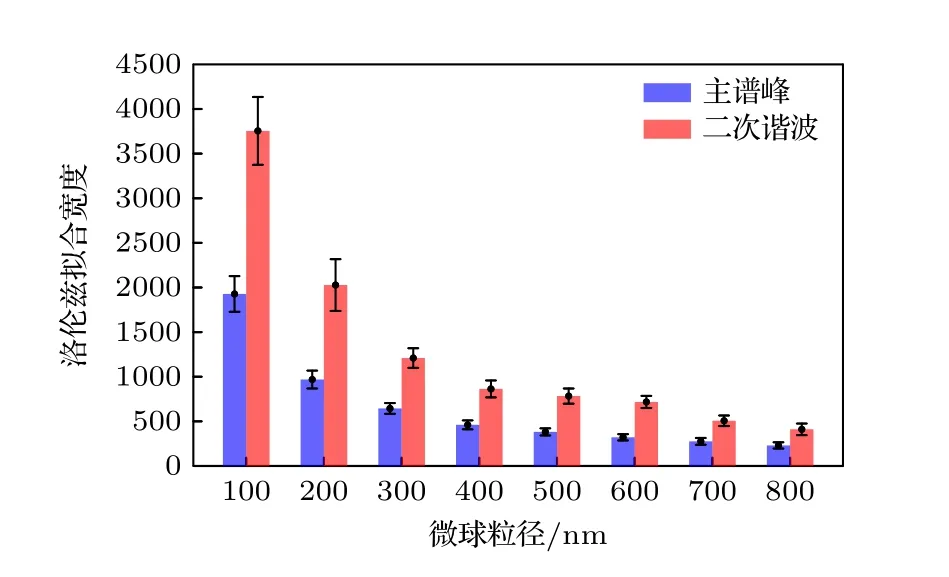
图8 不同粒径激光回馈信号功率谱的洛伦兹宽度Fig.8.Lorentz width of power spectra of laser feedback signals under different particle sizes.

最后,将本文提出的全新技术方案与已报道的两种方案进行简单的定性比较,结果如表3 所列.文献[10,15]中提出的方案(方案一)用恒流驱动的半导体激光器照射待测粒子,求得的功率谱峰中心在零频位置,仅能显示谱峰的右半侧.文献[12,13]中提出的方案(方案二)用微片固体激光器照射待测粒子,用一对声光移频器将功率谱峰搬离零频位置,移频量由两个声光移频器的+1 和–1 级衍射光的移频量所限定,不能随意调整.

表3 本方案与其他两种方案的定性比较Table 3.Comparison between this scheme and other two typical methods.

5 结论

本文提出了一种全新的方法来提升激光回馈纳米粒度检测的灵敏度,该方法通过对半导体激光器注入线性变化电流以实现线性调频,从而将功率谱峰从零频处搬移到任意频谱位置,同时在适当的光反馈强度下,功率谱峰的高次谐波会伴随着激光回馈信号条纹的倾斜而产生,这些高次谐波峰会呈现出相比于主峰整数倍的频谱展宽.该方法的理论模型在检测原理部分进行了相关推演.相应的仿真分析工作通过Python 语言完成,实验系统、实验条件及测试结果也相继给出.仿真分析结合实验测试结果表明,该方法可以有效地搬移功率谱峰并产生高次谐波峰,高次谐波峰宽度相比于主峰呈整数倍展宽,展宽后的高次谐波峰可以将粒度的微小变化成倍放大,有助于提高粒度检测的灵敏度.更多倍数的频谱展宽也对应着更低的信噪比水平,在实际测试中需要在二者之间作出平衡.该方法的物理内涵在于类正弦条纹倾斜引起的高次谐波,整个系统结构简单紧凑,易于实施,操作灵活,可以有效提升粒度检测灵敏度,有望应用于开发低成本、结构紧凑、高灵敏度的激光回馈粒度传感器或相关仪器.后续的研究工作将着重聚焦于测试这种灵敏度提升方法的纳米粒度检测效果,并进一步探索该方法的潜在应用场景.