V/Pd 界面氢吸附扩散行为的第一性原理研究*

张江林 王仲民 王殿辉 胡朝浩 王凤 甘伟江 林振琨3)†

1) (桂林电子科技大学材料科学与工程学院,桂林 541004)

2) (广西科学院高性能材料研究所,南宁 530007)

3) (南宁职业技术学院,南宁 530008)

采用钒/钯(V/Pd)金属复合膜渗氢是从混合气体中分离氢气的一种有效实用方法.为深入地了解催化Pd层与金属膜结合处的界面结构与吸氢/渗氢特性的关联性,进而提升合金膜提纯氢气的能力,本文采用基于密度泛函理论的第一性原理研究了V/Pd 金属复合膜界面的氢吸附/扩散行为.研究结果表明: 由于V/Pd 界面的电荷密度随着V/Pd 成键而增加,导致氢原子(H)溶解能随着接近界面而增大,在V/Pd 界面附近具有最高的溶解能(0.567 eV).氢迁移能垒计算表明,与H 沿V/Pd 界面水平扩散的最大能垒(0.64 eV)相比,H 垂直V/Pd 界面能垒(0.56 eV)更小,因而H 倾向于垂直V/Pd 界面进行迁移,并由Pd 层扩散到V 基体一侧,因V/Pd 界面处Pd 层的氢溶解能(0.238 eV)高于V 膜侧(—0.165 eV),H 将在界面的V 膜侧积累,易引起氢脆.V 基体掺杂Pd/Fe 的计算表明,与未掺杂的能垒(0.56 eV)相比,掺杂Pd/Fe 可明显地降低界面扩散路径中的最大能垒(0.45 eV/0.54 eV),利于氢的渗透扩散,且掺杂界面能一定程度抑制V 和催化Pd 层的相互扩散,提高复合膜的结构稳定性.

1 引言

氢能是人类战略能源的发展方向,氢气的分离提纯技术是氢能产业规模化应用的关键环节之一[1].钯及其合金(如Pd-Ag 合金)具有较好的氢渗透和抗氢脆的综合性能,是目前唯一实现工业应用的合金膜材料.但由于钯源稀有以及成本高等原因限制了其规模化应用.因此,非钯或少钯的新型氢渗透合金成为研究的热点.其中第5 族(V,Nb,Ta)金属的研究尤引人关注[2-4].具有体心立方结构(body centered cubic,BCC)的第5 族金属具有优良的氢扩散性能[5,6],氢扩散速率比面心立方相(face centered cubic,FCC)的Pd 以及其他金属晶体高出1 个数量级以上,其中V 金属的氢扩散系数最高(＞ 3.0×10—7mol·m—1·s—1·Pa—0.5,T≥ 320 ℃)[7].然而,V 直接用作膜材料仍存在一些问题,如V 表面的氧化[8]以及在低温下的氢脆效应[9].在V 膜材料上覆盖一层Pd 或Pd 合金,是解决这些问题的有效方法,氢气在镀Pd 的V,Nb 和Ta 膜中可以获得更高的通量,并且不容易受到氢脆影响[10].Alimov 等[11]发现,氢气通过100 mm 厚的Pd-V-Pd复合膜的流量在标准状况下达到了2.4 mL/min.其他研究表明,由于存在弹性变形和界面能量,具有界面的层状材料有利于改善界面的热力学性能和吸氢性能[12].然而,在实际应用中常会提高膜的操作温度从而避免V 膜在低温下的氢脆效应,这会导致Pd 层与V 层的相互扩散,加速膜的失效[13].Ko 等[14]通过第一性原理方法证实了晶界扩散是V 层与Pd 层的相互扩散机制.本课题组采用第一性原理研究了H 在V(100)表面和内部以及通过过渡金属元素M(M=Mo,W,Pd 和Ni)掺杂对其热力学稳定性和氢渗透特性的影响[15,16].当前,V/Pd 界面研究多集中在实验方面,相关界面氢吸附扩散的机理研究还不够深入.

本文拟建立合理的V/Pd 界面模型,开展氢在V/Pd 界面氢吸附和扩散特性的第一性原理计算分析,以期揭示V/Pd 界面的相互作用及其对氢吸附扩散的影响和作用机制,为合理设计和改善V/Pd 储氢材料性能提供理论指导.

2 计算方法

本文第一性原理计算使用VASP 软件包[17,18].计算的过程中,交换关联函数采用Perdew-Burke-Ernzerhof (PBE)修正的广义梯度近似(generalized gradient approximation,GGA)函数[19]所描述,投影增强波(projector augmented wave,PAW)方法[20]被用来处理原子核-电子相互作用,k点网格采样分辨率为2π×0.025 Å—1(1 Å=10—10m).所有计算均采用了350 eV 的动能截止能量,能量和力的自洽收敛阈值分别设定为0.01 meV 和0.02 eV/Å,并采用一阶Methfessel-Paxton 函数处理费米面附近的电子占据情况.计算出的BCC 相的V 与FCC 相的Pd 的晶格常数为2.99 Å和3.94 Å,与先前的计算结果一致[21].为了寻找H 原子的最小扩散路径和过渡态,采用了爬行图像微动弹性带(CI-NEB)方法来计算优化后的初始和最终位置之间的H 扩散能垒[22,23].

3 结果与讨论

3.1 V/Pd 界面模型构建及稳定性

基于相关研究报道[24,25],考虑到V(3.03 Å BCC)和Pd(3.89 Å FCC)晶格常数失配度较大,本文选择了常见的V(110)与Pd(111)面沿着c方向进行堆叠来模拟V/Pd 界面模型.为了模型的合理性并节约计算资源,计算了V(110)和Pd(111)表面的表面能,用以确定原子层数.表面能定义为表面原子和块体材料中的原子的自由能之差[26]:

其中γs是表面能,Eslab是表面模型的总能量,u是块体材料中原子的化学势,n是表面模型中原子的数量,A是相应的表面积.为了避免周期性对表面结构模型影响,在模型c轴方向添加了一个15 Å的真空层.如图1 所示,V(110)面和Pd(111)面每两层和三层为一个周期.如表1 所列,随着层数的增加,V(110)面和Pd(111)表面能均逐渐稳定,因此采用了6 层V 和Pd 组成的界面模型.

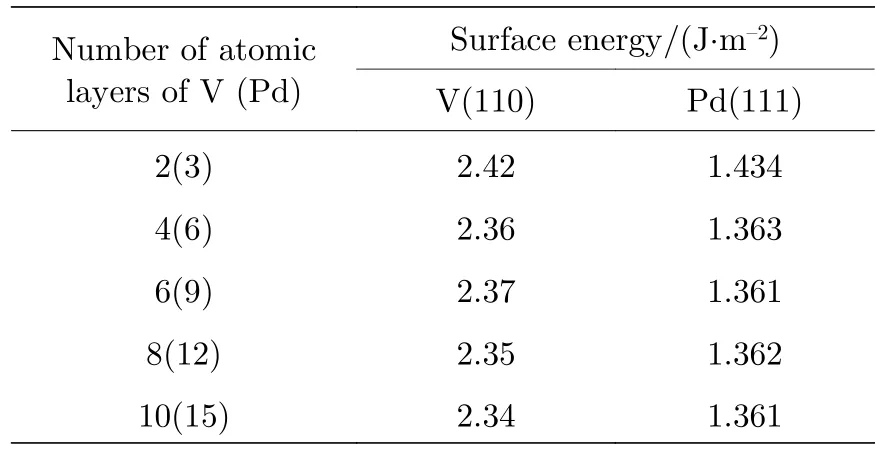
表1 不同厚度的V(110)面表面能Table 1.Surface energy of V(110) surface with different thickness.

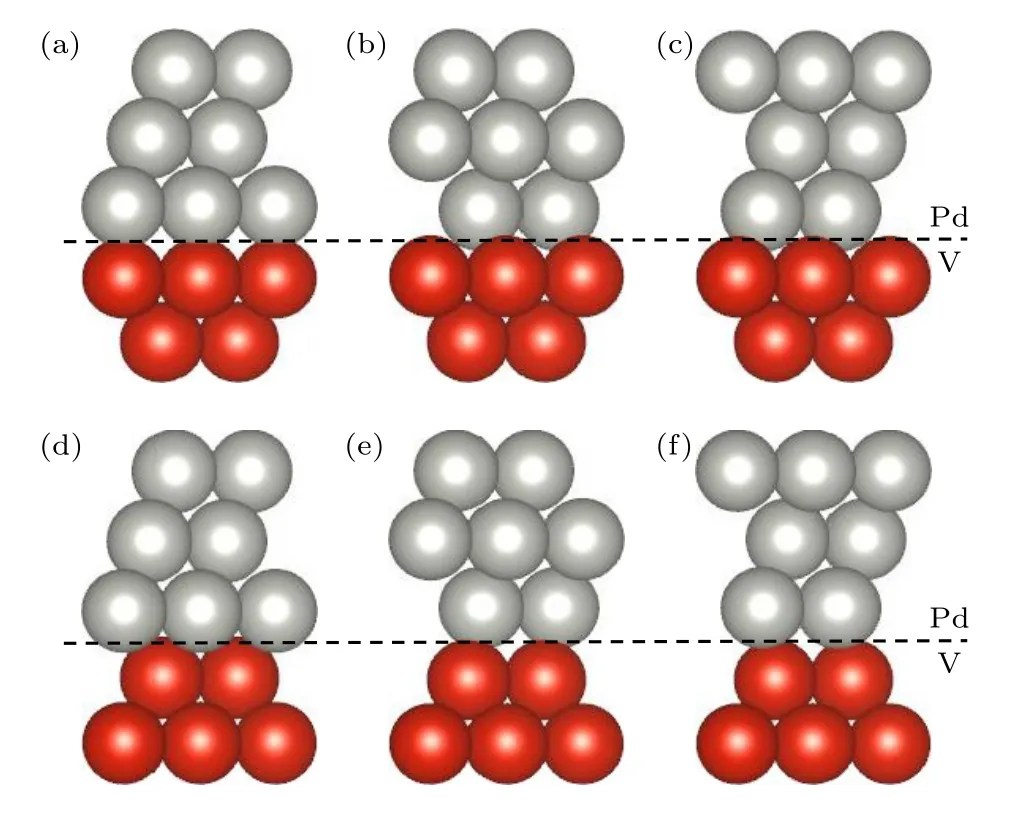
图1 V(110)面与Pd(111)面的6 种组合模型(Pd 原子为银白色,V 原子为红色) (a) AA';(b) AB';(c) AC';(d) BA';(e) BB';(f) BC'Fig.1.Six combined models of V(110) plane and Pd(111)plane (Pd atoms are silvery white and V atoms are red):(a) AA';(b) AB';(c) AC';(d) BA';(e) BB';(f) BC'.

通过旋转V(110)面使得其与Pd(111)面结合,界面失配度小于5%.如图1 所示,V(110)有A和B两种表面,Pd(111)有A',B'和C'三种表面,所以两者共有AA',AB',AC',BA',BB',BC'六种不同的组合模型.

为了确定最稳定的结构和合适的界面距离,采用 了UBER (universal binding energy relation)方法[27],计算了6 种结合模式在不同界面距离的理想黏附功,理想黏附功通常被用来定义将单位面积的界面结构分离成单独的表面结构所需要的能量[28].理想条件下忽略了结构的塑性变形和原子的扩散.可以由界面体系和孤立界面的能量差计算:

其中Ea和Eb表示组成界面结构的两个独立表面的总能量;Ea/b表示界面结构的总能量,A表示界面面积.图2 显示了V(110)和Pd(111)表面的黏附力与分离度的关系.AB'堆积界面在2.18 Å时的Wad最大,其次是AA'和BC'.因此,在进一步研究中采用了AB'耦合模型.在模拟界面时,固定了V(110)面底部两层和Pd(111)面顶部两层,并在模型c轴方向添加了一个15 Å的真空层.

图2 V(110)/Pd(111)界面的理想黏附功随着V 和Pd 原子层之间的分离的变化Fig.2.Change of ideal adhesion work of V(110)/Pd(111)interface with the separation between V and Pd layers.

界面模型两侧(V 侧,Pd 侧)中的块体、表面中部和界面三个不同区域的局域态密度(LDOS)分别标记(V1,Pd1),(V2,Pd2)和(V3,Pd3),结构如图3 所示.V 和Pd 都表现出明显的金属特性,界面处V 原子和Pd 原子的局域态密度在—6—0 eV 的能量范围内具有相似峰形,V3 的s 轨道与Pd3 的d 轨道存在明显的共振峰形,体现了界面处V 和Pd 原子的1 s—9 d 轨道杂化作用.另一方面,如图4 的界面电子局域函数图所示,上限值1表示电子完全局域化,而0 表示电子完全离域化[29].V 原子和Pd 原子之间的电子局域函数值约为0.3,说明界面处V-Pd 之间电子表现为离域特性,复合金属键的性质,V 和Pd 之间有较强的键合作用.

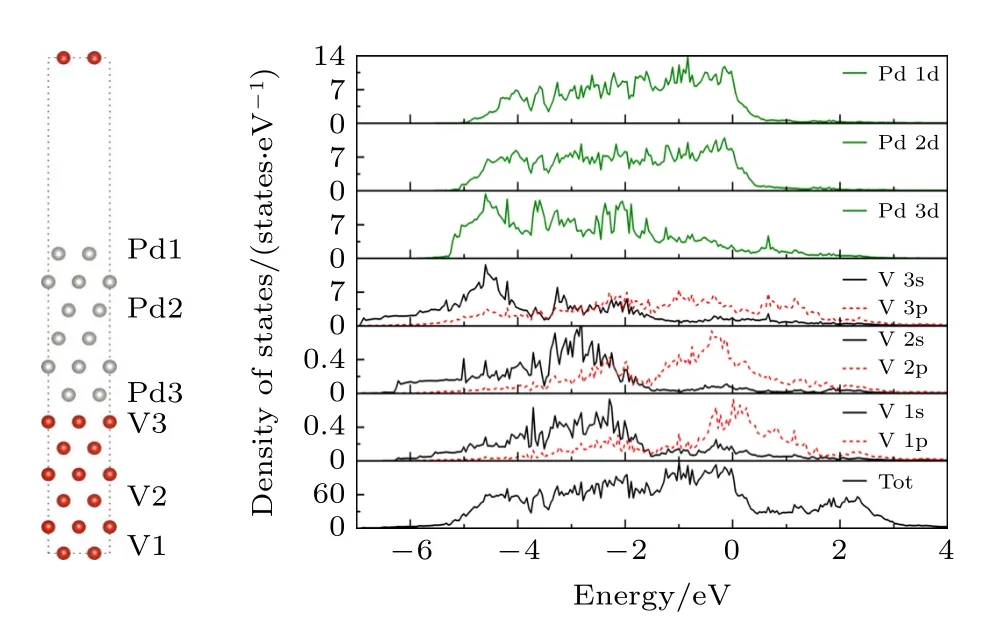
图3 V/Pd 界面模型和相应的局域态密度Fig.3.V/Pd interface model and the corresponding local density of states.

图4 V/Pd 界面电子局域化函数图Fig.4.Electronic localization function diagram of V/Pd interface.

3.2 氢原子在V/Pd 界面的溶解与扩散

为解析V/Pd 界面氢原子的渗透行为,首先研究了H 在界面附近的溶解和扩散情况,H 溶解能计算公式为

其中Etot是包含H 原子在内V/Pd 界面的总能量;EV/Pd是不含H 原子界面的能量;EH是H2分子能量的一半.氢溶解位置及其对应的氢溶解能如图5(a)和图6 所示.H 在V/Pd 界面溶解的可能位点有八面体位、四面体位以及伪八面体位置,如图5(b)—(d)所示.计算发现最初放置在伪八面体位点之间的H 在松弛后移动到四面体位点,这表明H 不能被困在伪八面体位点.由于界面的拉伸应变,V 层的层间距发生了收缩,Pd 层的层间距发生了拉伸.在Pd 层内,H 的溶解与Pd 块体中的氢溶解相似,H 更倾向于占据八面体位点,H 原子位于界面附近时也是如此.远离界面时,H 在四面体位置的氢溶解能为—0.030 eV,在八面体位置S2 的氢溶解能为—0.077 eV,比H 在Pd 中的溶解能要小[30].当界面Pd 侧中的H 靠近界面时,H 的溶解能逐渐变大并变为正,这与拉伸应变降低Pd 中H 的间隙形成能的效果相反[31],这将在第3 节详细讨论.先期研究证实,H 更倾向位于V-BCC 相晶体结构中的四面体位点,其溶解能约为—0.37 eV[21],在界面区域的H 溶解能量在远离界面时逐渐接近H 在V 块体中的溶解能.值得注意的是,H 在界面的溶解能都为正数,从能量角度来看,界面处不利于H 的占据.此外,从图6 的计算预测可以看出,由于界面处Pd 侧的H 溶解能均比在V 侧的高,H 将在界面的V 侧积累.

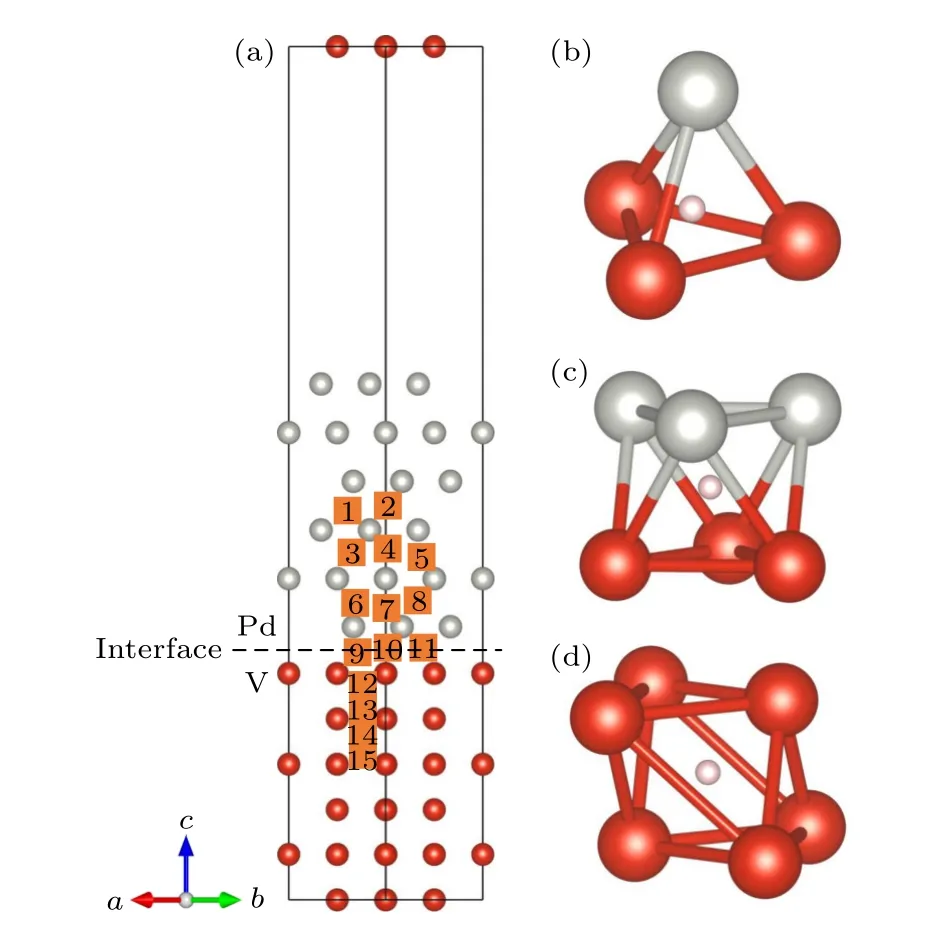
图5 (a) V/Pd 界面模型,其中方块表示H原子溶解的间隙位;(b) 四面体位置;(c)八面体位置;(d) 伪八面体位置Fig.5.(a) V/Pd interface model,where the square represents the interstitial position of H atom dissolution;(b) tetrahedron position;(c) octahedron position;(d) pseudo octahedron position.

图6 界面中不同位置上的氢溶解能Fig.6.Hydrogen dissolution energy at different positions in the interface.

H 的扩散势垒是评估H 扩散特性的关键,结合溶解能和缺陷/杂质的相互作用,可预测材料中的H 是否形成团簇造成氢脆[32].在计算V/Pd 层块界面附近的H 迁移能时,研究了H 在界面附近两种不同的扩散路径,其中一条是垂直于V/Pd 界面的扩散路径(图7),即S1→S2→S3→S4→S5→S6.H 原子由S1 跳跃到S2 的能垒为0.14 eV,这与块体Pd 中的迁移能垒(0.15 eV)相似.在从Pd 层到V 层的扩散路径上,S2→S3 的H 迁移能垒明显增加到0.56 eV,然而,S3 到S4 跳跃的能垒只有0.11 eV.这些结果表明,与体内的Pd 原子不同,界面处的Pd 原子似乎对H 有更大的排斥力,这将在下文讨论.越过V-Pd 界面进入V 原子层后,H 在V(110)的扩散更倾向于从当前四面体位到邻近四面体位,这与H 在金属V 中的体扩散途径类似.从S4 到S5,H 的激活屏障为0.09 eV.当H 从S5 到S6 继续向V 层深处移动时,由于H 经过了一条棱边,迁移的活化能垒升高至0.17 eV,同样接近H 原子在V 块体中扩散的势垒(0.165 eV)[15,21].

图7 H 垂直通过V/Pd 界面的迁移能量Fig.7.Migration energy of H passing through V/Pd interface vertically.

除了垂直于V/Pd 界面的H 迁移途径外,还研究了界面上H 的平行扩散.图8 展示了H 在V/Pd界面的两个最近的稳定八面体之间的迁移途径和扩散势垒.如图8(a)所示,由于H 在伪八面体位置不稳定,所以H 沿着八面体→四面体→八面体的路径迁移.H 在八面体→四面体→八面体路径扩散有两种不同的路径,路径Ⅰ: A→C→B,最大迁移能垒为0.64 eV;路径II: A→D→B,最高迁移能垒为0.44 eV(图8(b)).总之,在平行于界面的H 扩散必须克服0.64 eV 或0.44 eV 的能量障碍,而H 是否向Pd 界面移动决定了不同的迁移能量屏障.综上所述,从迁移能量角度分析,与V/Pd界面的平行扩散相比,H 在V/Pd 界面的扩散更倾向沿垂直方向迁移,并从Pd 层扩散到V 基体中,而不是从界面的V 侧扩散到Pd 层.计算结果也表明,H 从界面的Pd 侧到V 侧的低扩散势垒将起到促进H 进入V 的作用,从而强化V-Pd 复合薄膜的扩散性能,并促进V 中H 团簇的形成.

图8 水平通过V/Pd 界面的迁移能量Fig.8.Migration energy through V/Pd interface horizontally.

为探究H 原子在V/Pd 界面附近不同位置时的成键机制,计算了H 在界面的电荷密度.图9(a)—(d)显示了V/Pd 界面的电荷密度(e/Bohr3)分布.其中,图9(a)为没有H 原子的界面电荷密度图,图9(b)—(d)分别为H 原子在图5(a)中1,7,9 位置的电荷密度图.在物理学中,金属中的氢溶解能可以通过氢在均匀电子气中的溶解能近似理解,H 的溶解能量随着电荷密度的增加而减少,直到在最佳电子密度2.67×10—3e/Bohr3时达到最小值,然后随着电荷密度的进一步增加而增加[33].如图9所示,V/Pd 界面两侧的电荷密度均高于H 溶解的最佳电荷密度.同时,除了因为晶格匹配导致的电荷增加外,界面V 原子与Pd 原子的成键导致界面附近H 间隙位点的电荷密度进一步增加,因此,H 在V/Pd 界面附近具有最高的溶解能.

3.3 V 基体掺杂对V/Pd 界面渗氢性能的影响

掺杂是改善V 金属抗氢脆性能的一种有效方法.而最近的研究表明,元素掺杂也可抑制V 和Pd 的相互扩散,提高合金膜的氢渗透性能[34].Pd,Fe 掺杂对V/Pd 界面H 迁移能量的影响见图10,Pd 掺杂的S2→S3 的能垒为0.45 eV,比纯V/Pd界面(0.56 eV)降低了0.11 eV,S3→S4 的能垒为0.34 eV,比纯V/Pd 界面(0.11 eV)增加了0.23 eV.Fe 掺杂的S2→S3 的能垒为0.54 eV,S3→S4 的能垒为0.17 eV.如图11 所示，Fe 掺杂V 基体后,Pd 原子向V 基体空位扩散的势垒增加为0.48 eV,同时,在Pd 掺杂V 基体后,Pd 原子向V 基体空位扩散的势垒增加为0.39 eV,表明Fe 和Pd 掺杂后可以抑制Pd原子的扩散.

图10 (a) H 在Pd 掺杂界面的垂直扩散;(b) H 在Fe 掺杂界面的垂直扩散;(c) H 垂直通过掺杂界面的迁移能量Fig.10.(a) Vertical diffusion of H at the Pd doping interface;(b) vertical diffusion of H at the Fe doping interface;(c) migration energy of H through the doping interface vertically.

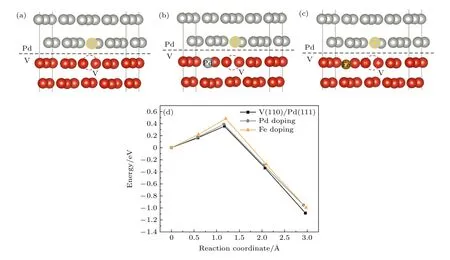
图11 (a) Pd 向V 空位的扩散;(b) Pd 向Pd 掺杂界面中V 空位的扩散;(c) Pd 向Fe 掺杂界面中V 空位的扩散;(d) Pd 向V 空位的扩散能垒Fig.11.(a) Diffusion of Pd to V vacancy;(b) diffusion of Pd to V vacancy in Pd doped interface;(c) diffusion of Pd to V vacancy in Fe doped interface;(d) diffusion energy barrier of Pd to V vacancy.

图12(a)和图12(b)显示了H 在S4 位置的电子局域函数图,Pd—H 键的长度为1.79 Å,Fe—H键的长度为1.67 Å,H 原子和金属原子之间的电子局域函数值约为0.5,表明V/Fe/Pd—H 键由金属键和共价键混合而成.在图10 中,Pd 对H 的相互作用使得H 远离了Pd 原子,相较于Fe 掺杂,S2→S3 的扩散路径缩短,扩散能垒降低,S3→S4的扩散路径增加,扩散能垒增加.同时,原子半径较小的Fe 原子掺杂增大了扩散间隙,使得H 原子能更容易地从S3→S4 扩散[14].图12(c)和图12(d)为Pd 原子扩散最终位置的电荷密度图,可知Pd 原子更偏向与V 原子成键,而不是与Pd 原子或Fe 原子成键,因为Pd 原子和V 原子的电负性相差最大,因此Pd/Fe 掺杂可以抑制Pd 原子向V 基体的扩散.

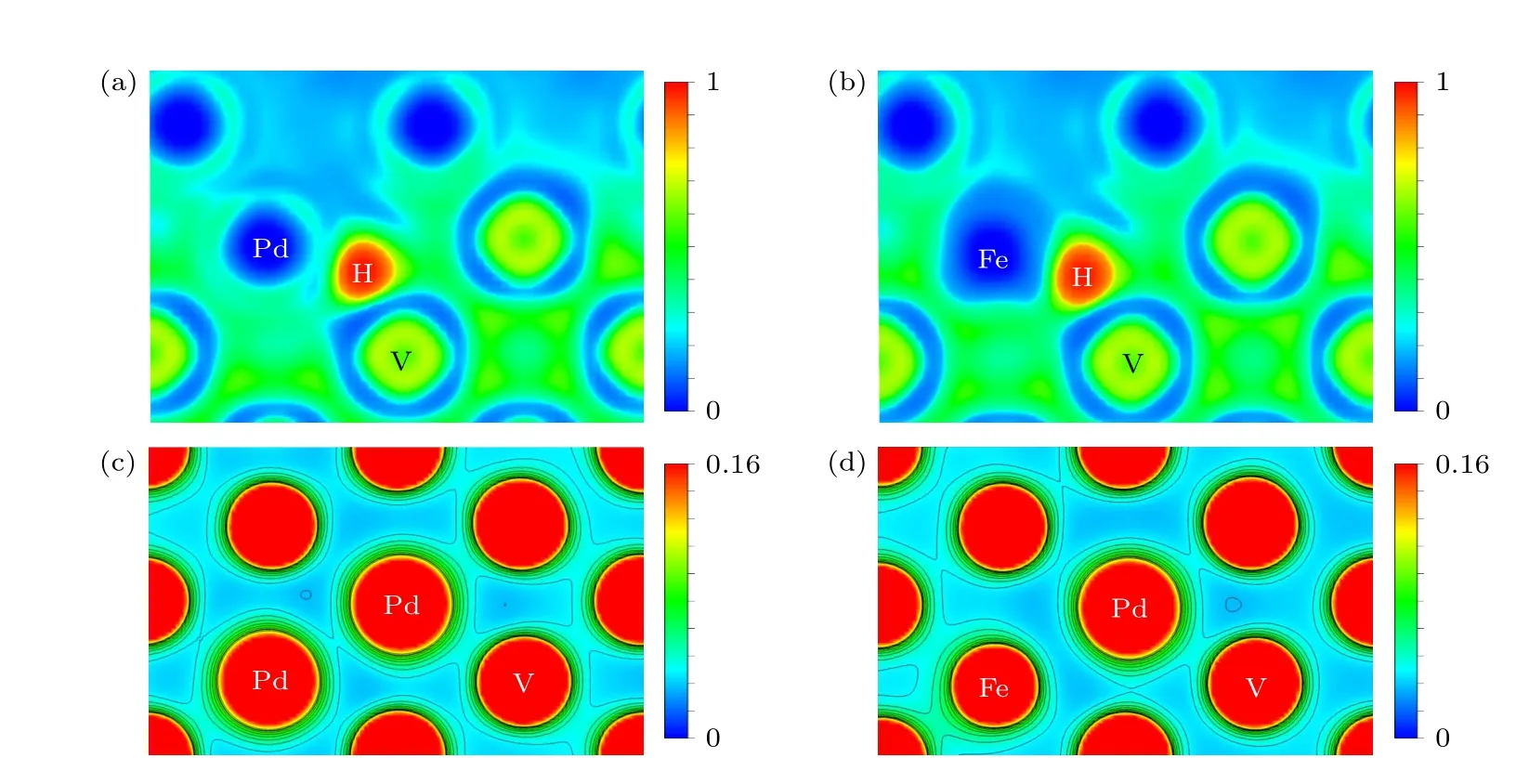
图12 (a) H 在Pd 掺杂界面S4 位置的电子局域函数图;(b) H 在Fe 掺杂界面S4 位置的电子局域函数图;(c) Pd 在Pd 掺杂V 基体空位的电荷密度图;(d) Pd 在Fe 掺杂V 基体空位的电荷密度图Fig.12.(a) Electronic local function diagram of H at S4 position of Pd doping interface;(b) electronic local function diagram of H at S4 position of Fe doping interface;(c) charge density diagram of Pd in Pd-doped V matrix vacancies;(d) charge density diagram of Pd in Fe-doped V matrix vacancies.

为了探究掺杂对V/Pd 界面力学性能的影响,采用第一性原理拉伸对V/Pd 复合界面进行拉伸测试.如图13(a)所示,无掺杂的界面拉伸应变率为12.5%时,达到了弹性强度的极限19.41 GPa.此时,拉伸模型中原子重新排列,完成第一次变形过程,即弹性变形阶段结束,之后继续拉伸,模型开始弹塑性变形过程,逐渐失去抵抗变形能力.Fe 与Pd 掺杂后界面的最大拉应力均略微下降,分别为15.52 GPa 和15.07 GPa.同时,在观察模型拉伸断裂面时,发现断裂位置均为界面处与V 结合的Pd 原子层,为此,对V(110)与Pd(111)方向进行了拉伸测试,发现Pd(111)的弹性强度极限(22.90 GPa)明显低于V(110)的35.25 GPa.此外,可能由于界面处V 原子层与Pd 原子层的成键,增加了界面周围的电荷密度,形成了一个电荷密度浓密的区域,加强了界面强度,但这也影响了界面附近Pd 原子层之间的强度,降低了界面Pd 原子层的理论拉伸强度.以上结果表明在制备V/Pd 复合薄膜时,应特别注意V 基体的表面状态并做合适的处理,如基体的预热等.

4 结论

本文采用第一性原理计算分析了H 在V/Pd界面的吸附和扩散行为,得到的主要结论如下.1) 采用常见的V(110)与Pd(111)面沿着c方向进行堆叠来构建V/Pd 界面模型,结合表面能和界面失配度,选取AB'组合,V(Pd)原子层数为6 的界面模型.2) 态密度和电荷密度分析证实,界面处V 与Pd 原子有很强的键合作用,H 在界面的溶解能最高,而在远离界面的溶解能逐渐接近H 在V 或Pd 块体中的溶解能值.3) 氢原子迁移能垒计算表明,与平行V/Pd 界面扩散相比,H 倾向于垂直V/Pd 界面进行迁移,并扩散到V 膜一侧.此外,因V/Pd 界面处Pd 层的氢溶解能高于V 膜侧,H 将在界面的V 膜侧积累,易引起氢脆.4) V 基体表面掺杂Pd 和Fe 的计算表明,虽然Fe 与Pd掺杂后界面的最大拉应力均略微下降,但是掺杂可明显降低界面垂直扩散路径中的最大能垒,利于氢的渗透扩散,并且能一定程度抑制V 基体和Pd 催化层的相互扩散,提高复合膜结构和性能.上述计算结果可为V/Pd 复合膜的设计与制备提供理论指导.