运动感应涡流磁场检测中的激励磁场优化设计方法

李恺翔 刘润聪

(中国科学院大学材料科学与光电技术学院,北京 101408)

在生产或使用过程中,薄金属板中会产生微缺陷(微颗粒或气孔),这些微缺陷的数目及尺寸决定了薄金属板的品质,影响其使用寿命和安全系数.因此,对微缺陷进行定量和准确的表征是保证薄金属板产品品质与使用安全的必要条件.电磁检测中的运动感应涡流磁场检测可应用于检测导电非导磁材料中的缺陷.本文通过模拟和实验结果显示,当提离距离、永磁体表面剩磁确定时,永磁体尺寸与缺陷检测信号幅值正相关.另外,提出一种运动感应涡流磁场检测中激励磁场的优化方法,由该方法产生的两种永磁体阵列相比于同体积、同表面剩磁的简单永磁体,产生的缺陷检测信号幅值更高,因而可以提高检测的灵敏度.

1 引言

薄金属板是一种在工业领域具有广泛应用的重要冶金产品.在生产或长期使用过程中,薄金属板中会产生缺陷[1−4],这些缺陷会损害结构的完整性,在特定应用场合导致事故.因此,为保证和保持材料的性能,缺陷的检测至关重要.根据应用场景、测量对象等要素,有多种无损检测方法可用于检测缺陷,如漏磁[5,6]、超声[7,8]、光学检查[9,10]以及涡流检测法[11−13].

运动感应涡流磁场检测(motion induced eddy current magnetic field testing,MIECMF)方法是涡流检测法的一种,由Ramos 等[14]在2013 年首次提出.他们研究指出MIECMF 方法的灵敏度随速度的增大而增大,因此在诸如生产流水线这类样品本身在运动的应用场景下,该方法是一种非常适合的检查方法.目前已有研究证明了MIECMF 方法检测缺陷的有效性.Rocha 等[15]将MIECMF 方法应用于表面和亚表面缺陷的检测,并指出在较高的速度下,较深的涡流扩散所需的时间,也使得通过测量永磁体的运动距离来估计亚表面缺陷的深度成为可能.Feng 等[16]将MIECMF 方法用于检测金属管道中的缺陷,研究结果显示,该方法可以用于识别管道的内缺陷与外缺陷.Brauer 等[17]研究了应用运动感应涡流检测(motion induced eddy current testing,MIEC)技术评价搅拌摩擦焊接性能的方法.Yuan 等[18]通过MIECMF 方法提出了一种定量表征运动铁磁材料裂纹的方法,结果指出直流电磁系统基于MIEC 不仅可以检测铁磁金属,如轴承、齿轮等,而且可对非铁磁金属内部裂缝进行定量表征.

在一些应用场景中,需要对尺寸较小的缺陷(几十到几百微米)进行检测.在检测微小缺陷时,MIECMF 方法的灵敏度由于其原理受到硬件条件的限制,该方法需要激励磁场的永磁体,其磁场比一般电磁系统强,但常用的永磁体材料的表面剩磁最高也只能达到1 T 左右.永磁体表面到导电板之间的距离被称为提离距离,而该参数也因传感器或拾取线圈的尺寸和运动机构的机械误差等因素,而具有明显的限制.此外,导电板的电导率等参数也是该方法的制约因素之一,因此优化第一磁场布置是少数可行的方案.本研究的目的是在激励磁场、提离距离及检测对象电导率等因素确定的情况下,通过调整磁体的布置方式来提高测量方法的灵敏度.

针对MIECMF 检测导电非导磁金属板中微缺陷问题,本文提出了一种第一磁场优化设计方法.该方法不仅指出了MIECMF 方法中缺陷信号幅值的决定因素,还解释了前人研究中对激励磁场优化尝试面临挑战的原因,这可以为激励磁场优化提供新的思路.

2 理论与模型

2.1 MIECMF 基础

MIECMF 方法基于运动感应涡流现象对导电非导磁材料薄板中微缺陷进行检测[14].如图1 所示,其利用激励磁场(一般是永磁体或通电螺线管,又称为第一磁场)与所检测的导电板之间的相对运动产生运动感应涡流.由于导电板中存在由腐蚀导致的缺陷或凹坑等不连续性,其电导率的空间分布不均匀,会影响运动感应涡流的路径及其产生的磁场(以下称为第二磁场).通过测量材料表面附近的磁场,可以确定缺陷的数量与尺寸.

图1 运动感应涡流检测原理 (a)无缺陷;(b)有缺陷Fig.1.Principle of motion induced eddy current testing: (a) Without defect;(b) with defect.

如图1(a)所示,运动感应涡电流是导电板与第一磁场存在相对运动产生的,表现为导电板运动切割磁感线.根据电磁学原理,感生电动势主要集中于导电板内永磁体正下方的区域,该区域的尺寸与永磁体相当,即电敏感区(electric sensing zone,ESZ).运动感应涡电流的电流密度可通过欧姆定律求出:

其中J为电流密度,v为永磁体与导电板的相对速度,B为第一磁场的磁通密度,E为电场强度,σ为导电板材料的电导率.显然,当导电板材料固定时,相对速度与第一磁场提供的磁通密度越大,ESZ 中电流密度越大.欧姆定律从另一角度说明了该方法中的ESZ 等同于导电板中第一磁场磁通密度较大的区域.

当检测对象中的微缺陷随相对运动进入检测区域时,如图1(b)所示,由于缺陷与金属材料的电导率不同,运动感应涡电流会发生畸变.畸变后的涡电流可被视为在原始电场上增加了一个畸变相,用ΔJ表示.第二磁场的变化量可用于表征缺陷,并通过毕奥-萨伐尔定律计算:

其中dl为载流体的线元,r为电流元到磁场检测点的径矢,er为该径矢的单位向量,µ0为真空磁导率.

2.2 建模方法

本文使用COMSOL Multiphysics[19]有限元模型元素求解器获得数值结果.MIECMF 主要涉及电学与磁学,建模和计算时有以下几个假设与设置.

条件1在低磁雷诺数条件下,所有结果使用瞬间稳态解.

磁雷诺数Rem是影响ESZ 区域的关键参数之一,定义为磁对流相与磁扩散项之比,其物理意义为激励磁场与感应磁场之间比率的量度,磁雷诺数的表达式为

其中L为该问题中的典型长度标度,µ为磁导率.Wang 等[20]研究表明低雷诺数的情况下(Rem≪1),ESZ 尺寸与使用的永磁体尺寸相当.Yuan 等[18]还通过改变速度间接调整Rem的方式,观察到相对速度增大时ESZ 会发生变形(拖拽效应),表现为ESZ 沿相对速度方向发生偏移,Rem越大偏移越明显.Brauer 等[21]指出当Rem较大时(Rem≫1),会产生与趋肤效应类似的现象,表现为ESZ 的深度与相对速度为负相关关系.显然,Rem较大时,ESZ 中的电流密度会更可观,但该情况下ESZ 的形状更复杂,这使得涡流的计算与第二磁场的计算都具有一定难度.相反,Brauer 等[21,22]研究还指出低Rem时,第一磁场可看作一个固定不变的磁场,空间中总磁场的变化只由第二磁场变化引起,这样既简化了第二磁场测量,也更有利于参数分析.

显然,在低Rem条件下,导电板移动对ESZ 区域形态的影响可忽略.导电板在磁场中运动过程中的每一时刻,涡电流与第二磁场均处于稳态.导电板在第一磁场中运动过程的瞬态解,可视为每一时刻下稳态解的集合.本研究采用的相对速度较小,并将导电板在第一磁场中的运动的瞬态过程按照运动时间拆解成系列稳态研究[20,22].

条件2永磁体空间区域以外部分的相对磁导率相同.

Marek 等[23]研究指出,微缺陷通过两种机制造成总磁场发生变化: 1)由于空气、导电板和微缺陷的相对磁导率不同,微缺陷移动对第一磁场磁感线造成扰动;2)微缺陷的存在使得电导率不连续,导致运动感应涡流重新分布,从而导致第二磁场发生变化.对于导磁材料板,第一机制为主要原因;对于非导磁材料板,第二机制为主要原因.

为研究非导磁材料中缺陷引起的空间第二磁场变化,需消除磁导率差异的影响.因此,将空气域、导电板和微缺陷的相对磁导率设为相同值(µr=1).根据表1,该设置显然不会引起较大误差,该方法能消除第一磁场可能的变化,突出第二机制的作用,同时也简化了计算.

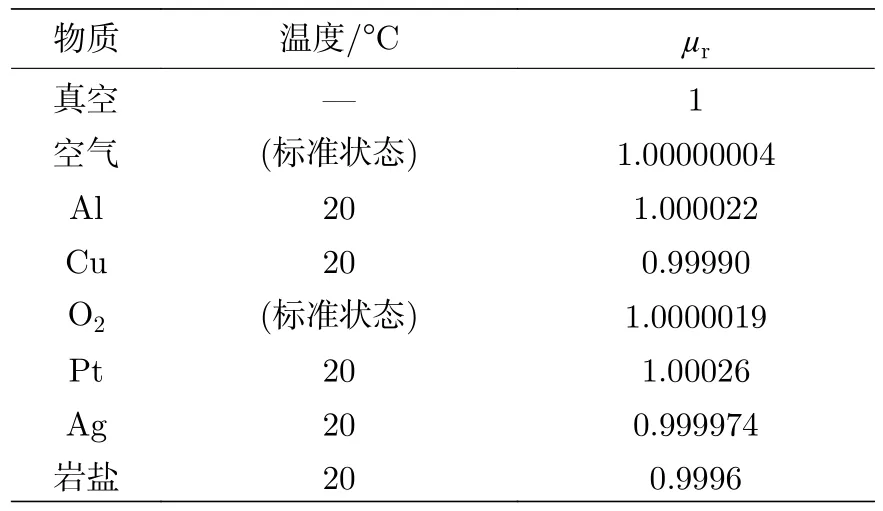
表1 常见物质相对磁导率Table 1.Relative permeability of common materials.

条件3磁体的默认布置方式为上下对称.

上下对称的永磁体设置是对于导电薄板(厚度远小于提离距离与永磁体尺寸),将两个相同磁化方向的永磁体固定在导电薄板上下距离相等的位置,Moreau 等[24]在推导涡电流解析式的研究中提出了这种永磁体布置方式.该方法中整个导电薄板均可以视为处于图2 中Z方向的磁场中,该布置方式下,导电薄板中涡流的Z方向分量均为零,进而简化第二磁场的计算.

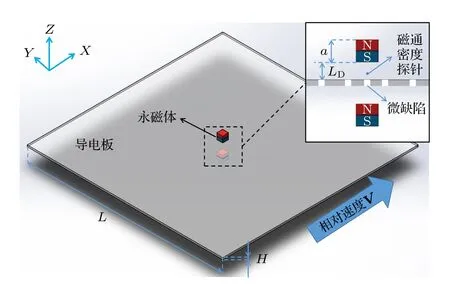
图2 数学模型示意图Fig.2.Schematic diagram of mathematical model.

根据以上假设,在选定导电板为参考系时,由于导电板可看作无穷大平面(实际建模中并非无穷大),虽然在模型中可设定导电板具有相对速度,但其空间位置不变.同样永磁体与磁通密度探针(探针为虚拟的,非物理概念.经检验,不会影响电磁场分布)坐标也不变化.模拟时计算瞬时稳态解,相对运动过程仅有缺陷沿相对速度方向上的位置变化体现.

本节所建立的数学模型如图2 所示,笛卡尔坐标系的原点选在导电板的体心处.立方体缺陷具有固定边长,且贯穿导电板.两个永磁体在导电板上下对称设置,称为一个永磁体组.永磁体为边长为a的立方体,其材料选择为BMN-35.设提离距离LD,表示导电板上方永磁体的下端面到导电板上表面的距离.磁场检测的探针点处于永磁体轴线上,距导电板表面距离为0.5 mm.各部分材料的磁导率、电导率、永磁体磁化程度以及提离距离固定,永磁体的尺寸和磁化方向可以调节.

该模型中的网格划分均采用自由四面体网格,每部分中的网格单元尺寸设定为该部分最小尺寸的50%—20%.其中对于中心在原点处、边长为40 mm 的立方体内空气域进行较细化网格设置,以在提高求解精度的同时缩短计算时间.数值模拟部分参数见表2,模拟中所用网格划分足够多,经检验在目前基础上约再增加网格数量的17 倍,模拟结果差异在1%以内.

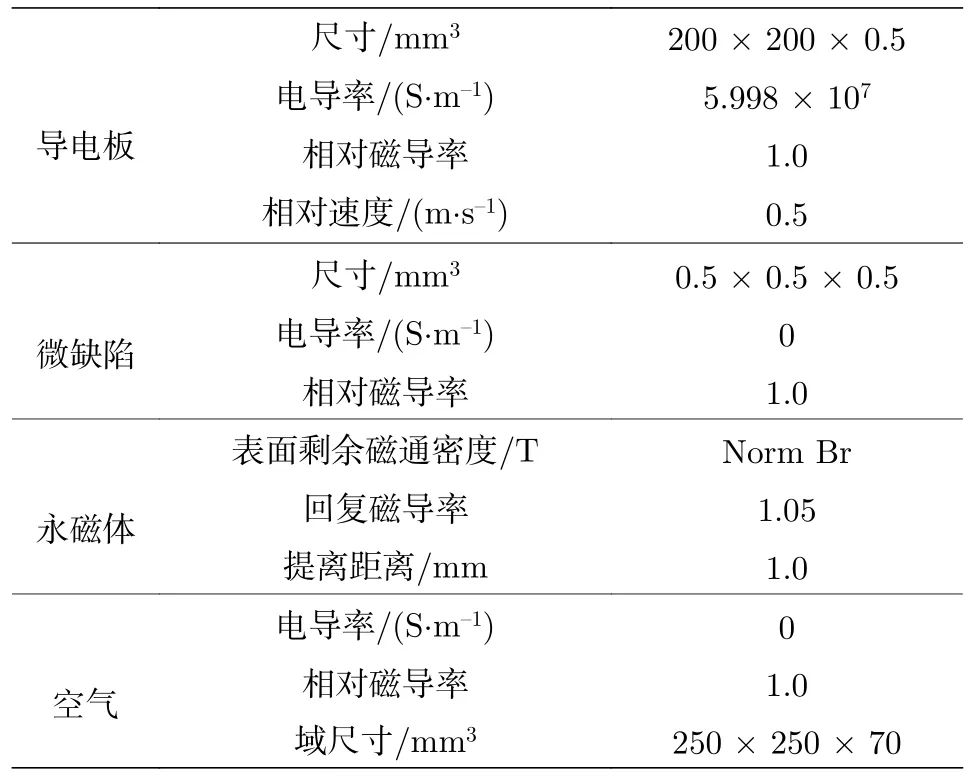
表2 数值模拟部分参数Table 2.Parameters of numerical simulation.

导电板内各处的电流密度在实验中无法被准确测量,但通过模拟的方法得到的电流密度分布,却可以为第一磁场优化方法提供依据.导电板内电流密度及缺陷信号获得方法如图2 所示.导电板内沿X轴预设多个带有电流密度探针的缺陷结构.在导电板内部预设一些立方体型的区域,在此基础上进行网格划分,而在后续模拟时根据需要将相应区域的电导率设置为导体或缺陷.这种做法能保证在所有模拟中网格划分一致,否则每次模拟网格划分会因缺陷分布带来的形貌差别而略有差异,进而带来模拟误差.在上述立方体区域内设置电流密度探针,且仅在导电板内无缺陷时启用,从而得到缺陷路径上的电流密度分布.在与后续实验中磁场传感器处设置磁通密度探针,且仅在导电板内存在缺陷时启用,从而得到缺陷引起的第二磁场变化.

2.3 ESZ 对缺陷信号的影响

本节讨论缺陷信号与永磁体尺寸的关系.原理上是由永磁体与导电板相对运动产生涡电流,再由涡电流产生第二磁场,因此分两步讨论: 即先讨论ESZ 中的感应电流和永磁体尺寸关系,再讨论ESZ 中的感应电流和缺陷信号关系.

2.3.1 永磁体尺寸对ESZ 的影响

首先研究当导电板中没有缺陷时,永磁体尺寸与ESZ 中电流的关系.设相对速度v=0.5 m/s,沿X正半轴,提离距离LD=1 mm,永磁体剩余磁通方向ez=1 ,控制永磁体边长a为变量,a=1,2,4,6,8 和10 mm.缺陷移动路径上各点处电流密度的Y方向分量的变化如图3 所示,其中每个负峰的宽度体现了该情况下ESZ 的尺寸.显然,在永磁体尺寸a从1 mm 增至10 mm 过程中,ESZ 尺寸增大,且ESZ 中电流密度模增大.此外还可以明显观察到,电流密度的Y方向分量在ESZ 内外方向相反.

图3 永磁体尺寸对缺陷运动路径上各点处电流密度的Y 方向分量的影响Fig.3.Influence of permanent magnet size on the Y-direction component of current density at each point on the defect motion path.

永磁体与原点处电流密度模的关系如图4 所示,显然两者为正相关关系.考虑到模拟中提离距离设置为1 mm,当永磁体尺寸接近10 mm 或更大时,原点处的电流密度模达到该方法的极限.换言之,当永磁体尺寸达到提离距离的10 倍之后,继续增大永磁体尺寸,原点处电流密度模不再有明显增长.这主要是因为当永磁体尺寸达到提离距离的10 倍之后,继续增大永磁体尺寸,原点处电流密度模不再有明显增长,如图5 所示.分析认为,随着永磁体的增大,原点处的第一磁场Z方向分量BZ不再有明显增长.永磁体尺寸增大,原点处磁通密度的Z方向分量趋于表磁,这也决定了电流密度的上限.

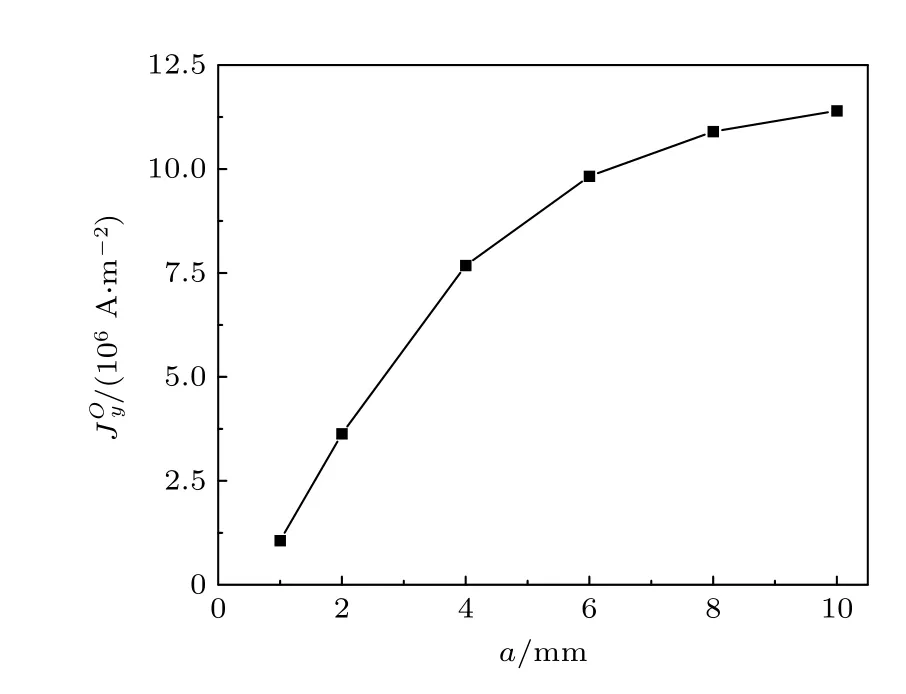
图4 永磁体尺寸与原点处电流密度模的关系Fig.4.Relationship between permanent magnet size and current density mode at the origin.

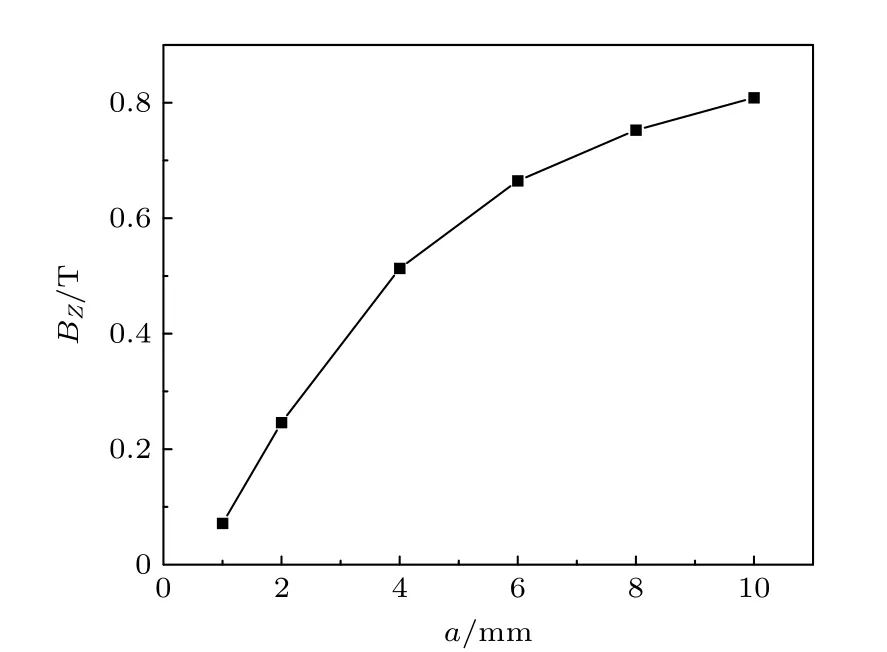
图5 永磁体尺寸与原点处第一磁场Z 方向分量的关系Fig.5.Relationship between permanent magnet size and Z direction component of the first magnetic field at the origin.

对图3 和图4 中电流密度模的量级需进行验算.在验算过程中,为方便起见只验算(1)式中括号里B×v项.为贴合实际,采用工业中更实用的铜电阻率(ρ=1.75×10–8Ω·m).则铜电导率σ=5.7×107S/m,速度v=0.5 m/s.而磁通密度B,可以从模拟结果中得到.在没有导电板与缺陷的情况下,模拟得到原点处Z方向的磁通密度分量BZ约为0.8 T.如表2 所列,在模拟过程中永磁体的剩余磁通密度仅由材料BMN-35 决定,为更好地重复该模拟,故没有修改Comsol 软件的材料库.BZ的取值由永磁体的材料与相对位置决定.

将以上数据代入,确实可以得到该电流密度为106—107A/m2.模拟结果依然合理,因为模拟中所用的0.8 T 是一个日常环境中很强的磁场,对于永磁体来说只有在其近表面磁场才能达到该强度.且后续研究发现,虽然其电流密度模很大,但对应的电势差其实很小(在mV 量级),而这个看似很大的电流密度模,由于导体的运动故在导体的每个区域作用的时间也很短,不会对其产生明显影响.因此这个结果是合理的.

而缺陷移动路径上各点处电流密度的X方向分量,其电流密度模远小于Y方向分量且规律不明显.根据系统的对称性,理论上在X轴线上也不存在X方向的电流,故此X方向的电流分量为计算误差.该误差绝对量随永磁体尺寸的增大而略有增大,这是由Y方向分量的增大导致.

2.3.2 永磁体尺寸对缺陷信号的影响

为研究永磁体尺寸a与缺陷信号的关系,在上述模拟参数不变的情况下,引入带有微缺陷的导电板.在a取相同变量值时分别进行模拟得出缺陷信号,其结果表示为缺陷移动位置X与点探针处磁通密度在X方向的变化量ΔBx曲线,如图6 所示.显然,永磁体尺寸与缺陷信号的幅值为正相关,且永磁体尺寸增大到一定值后,继续增大永磁体尺寸,缺陷信号幅值的提升将不再显著.

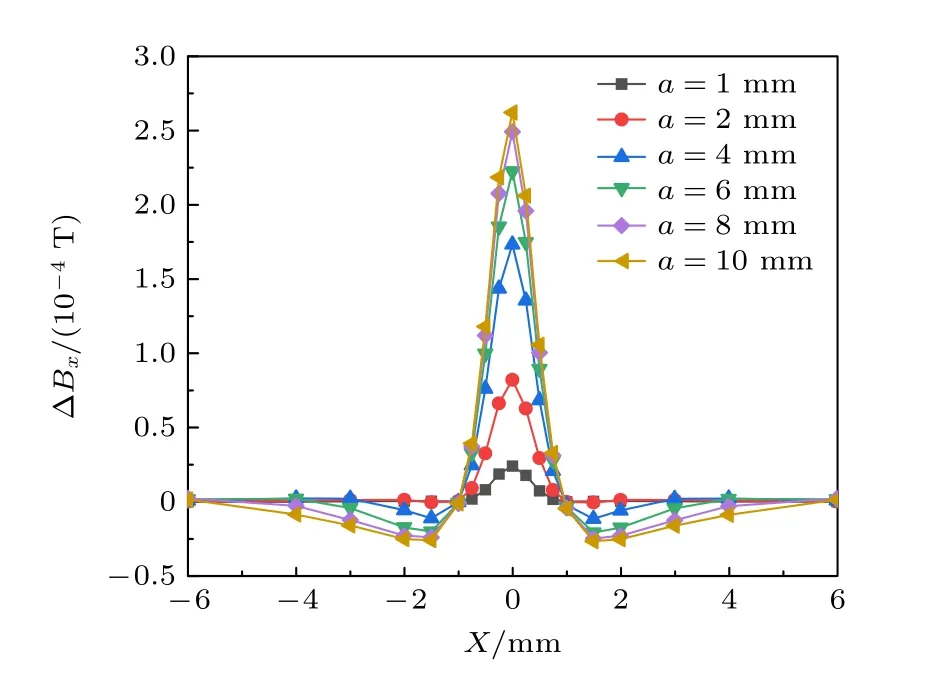
图6 缺陷移动位置X 与点探针处磁通密度的X 方向变化量曲线Fig.6.Curve of defect moving position X and X direction change of magnetic flux density at point probe.

使用相同方法得到缺陷移动位置X与点探针处磁通密度的Y方向变化量ΔBy曲线.由于探针处磁通密度的Y方向变化量ΔBy的绝对量远小于ΔBx,且理论上该方向的磁场变化为零,因此在实际测量时应将传感器敏感方向设置在X方向,以探针处磁通密度在X方向的变化量ΔBx表征缺陷尺寸.需要指出的是,在前人的研究中可以测得Y方向上微小的磁场变化[18].这是由于实验中,缺陷并不是严格从探针点下方经过.

对比以上结果不难看出,第二磁场在垂直于ESZ 中电流密度分量较大的方向上的变化量更大,其原因也可由毕奥-萨伐尔定律解释.实验中应该将传感器的敏感方向更多地设置在该方向上.

综上,得到永磁体尺寸与ESZ 中电流密度的关系,也得到了永磁体尺寸与缺陷信号关系.考虑到测量原理,改变永磁体尺寸其实是改变涡电流,因此考虑原点处电流密度模与缺陷信号幅值的关系.之所以选择在原点处,是因为: 1)低磁雷诺数的情况下,相对速度对ESZ 形状影响不大.由2.3.1 节结果可知,ESZ 在永磁体区域正下方.2)原点距离探针点距离最近,则原点处的涡流与探针点处的第二磁场变化量相关性最大.

如图7 所示,显然原点处电流密度模与第二磁场变化幅值呈线性关系,则可以认为: 在提离距离、相对运动速度与传感器位置等条件确定时,缺陷信号的幅值仅由原点处原始电流密度在Y方向的分量决定.换言之,提高原点处原始电流密度就能有效提高缺陷信号的幅值,进而提高MIECMF方法的检测能力.注意,在这里假设缺陷尺寸与提离距离相当或更小,若缺陷尺寸较提离距离更大,则在考虑涡电流时也需要考虑更大范围.

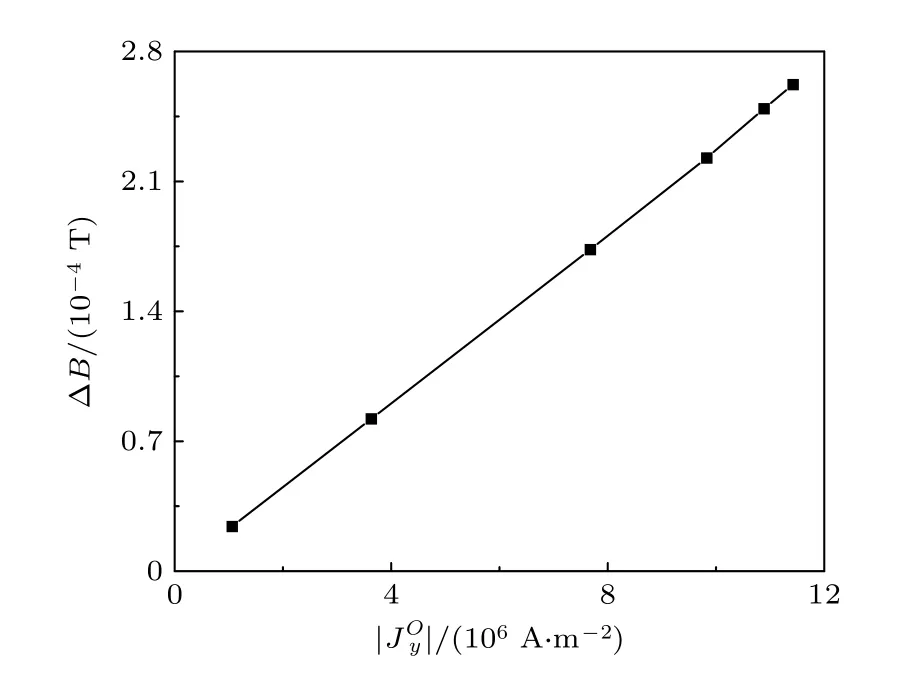
图7 原点处电流密度模与信号幅值关系Fig.7.Relation between current density mode at origin and signal amplitude.

2.4 缺陷信号取决于第一磁场设置

基于2.3.2 节中的结论,在永磁体尺寸外探索第一磁场设置方式优化的可能.本节研究方法是对于不同空间位置永磁体微分单元,考察其对原点处电势与电流密度在X和Y方向分量的贡献,并以此得出第一磁场优化设置.图8 为一个微分单元,其几何形状为贯穿永磁体区域的圆柱状体积元.

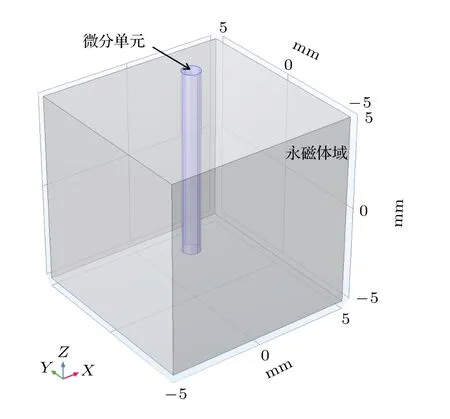
图8 微分单元选取示意图Fig.8.Schematic diagram of differential unit selection.

各永磁体微分单元的贡献获得方法为: 永磁体区域内磁导率固定.仅将该区域内的某个微分单元磁化,而同为永磁体区域、微分单元之外的部分设为没有磁化.在上述条件下,计算出在导电板内产生的涡流在原点处的电流密度与电压,即为该永磁体微分单元的贡献.在计算电势时,选取边缘处为电势参照点,电势为零.

依据磁场、电场服从矢量叠加原理,电势服从代数原理叠加以及电势的唯一性定理,显然各微分单元永磁体产生的电场服从上述叠加原理.对永磁体的微分操作不会引起电场畸变.

2.4.1 贡献计算

对于每个永磁体单元,其产生的运动感应涡流在原点处的电势与电流密度在X和Y方向分量,取决于该单元所处的空间位置.在边长a=10 mm的立方形永磁体(剩余磁通方向ez=1)中,取半径为0.5 mm,高为10 mm 的多个圆柱状微分单元(各微分单元间无重合体积),分别模拟每个微分单元产生的涡电流,并依据该涡电流在原点处的X方向电流密度分量、Y方向电流密度分量与电势的不同情况对整个永磁体进行划分,其结果如图9所示.

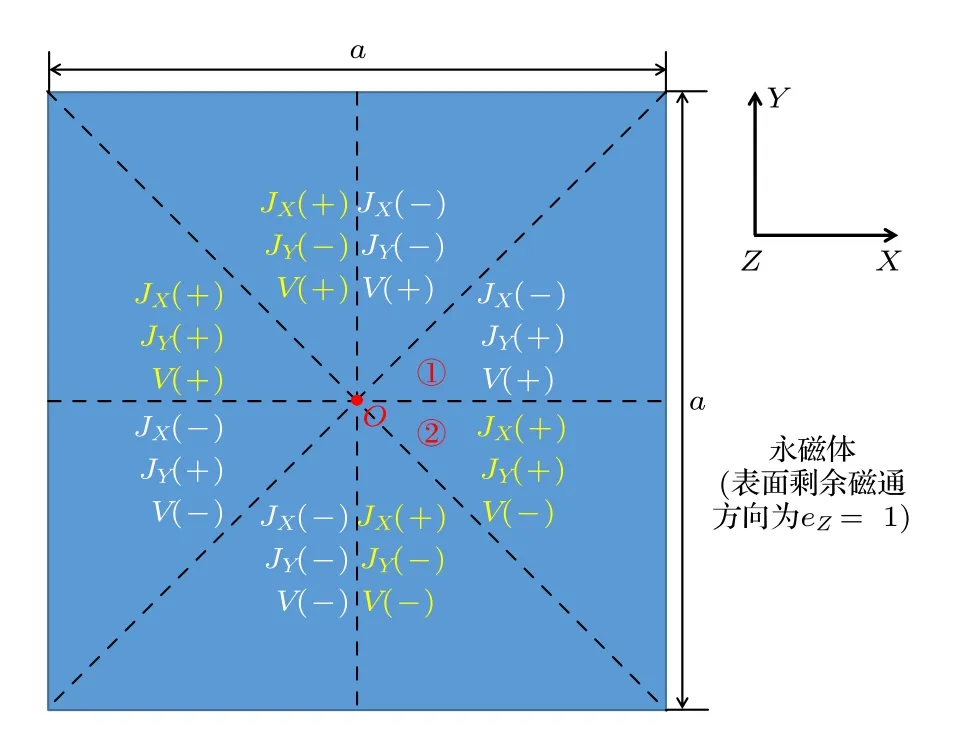
图9 永磁体依据运动感应涡流在原点处的电势与电流密度贡献分区,图中假设永磁体磁化方向为 eZ 方向,即永磁体N 级为Z+方向,导体板运动方向为X+方向Fig.9.Permanent magnet is divided according to the potential and current density contribution of the motion induced eddy current at the origin.In the figure,it is assumed that the magnetization direction of the permanent magnet is eZ direction,that is,the permanent magnet N is Z+direction,and the movement direction of the conductor plate is X+direction.

根据图9 中的结果,不难发现永磁体各单元产生的涡流之间存在“相互部分抵消”的情况.如标记区域①产生的运动感应涡流,其在原点处电流密度的X分量为负,而区域②则为正,这就使得永磁体各部分之间产生运动感应涡电流的效果相互部分抵消.则根据图9 中的结果,可选定电势或某方向电流密度分量为标准,将贡献为负的区域的磁化方向反向设置,从而使得永磁体阵列整体产生的运动感应涡电流场在原点处的电势或电流密度在某方向的分量增大,通过抑制“相互部分抵消”的情况以提高电流密度,进而得到幅值更大的缺陷信号.

将图9 中Y方向电流密度分量为负值部分的磁化方向反向设置得到图10(b),为聚Y方向电流设置.将图9 中X方向电流密度分量为负值部分的磁化方向反向设置得到图10(c),为聚X方向电流设置.将图9 中电势为负值部分的磁化方向反向设置得到图10(d),为聚集电势设置.其中聚集电势设置下的永磁体与Rocha 等[19]研究中的永磁体设置十分类似,后面也会讨论这种设置方式在提高缺陷信号幅值时遇到挑战的原因.而聚X方向电流设置下的永磁体与Feng 等[25]研究的永磁体设置十分类似.

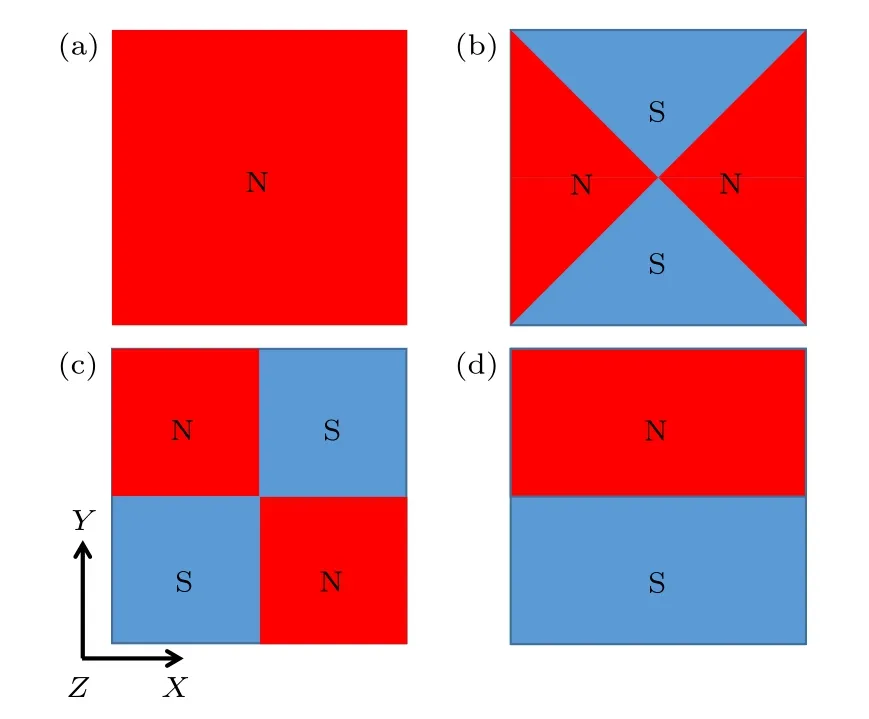
图10 第一磁场设置 (a)原始设置;(b)聚Y 方向电流设置;(c)聚X 方向电流设置;(d)聚集电势设置(表面剩磁方向平行于Z 轴;导电板相对速度方向平行于X 轴)Fig.10.Setting of the first magnetic field: (a) Original pattern;(b) pattern focusing current in Y direction;(c) pattern focusing current in X direction;(d) pattern focusing potential (The direction of surface remanence is parallel to the Z-axis;the relative velocity direction is parallel to the X-axis).

2.4.2 多种第一磁场设置下的涡电流分析

本部分建立的数学模型与2.3 节相同.考虑2.3.2 节中a=8 mm 与a=10 mm 时缺陷信号幅值提升不大,因而本节采用2.3 节永磁体尺寸的最大值a=10 mm 的情况,分别对2.4.1 节中3 种永磁体阵列形式的运动感应涡电流场与简单永磁体设置(以下简称原始设置)的差异,以及缺陷信号的改变.3 种永磁体设置产生的涡电流均需要与原始设置,即图11(a)部分,在原点处的Y方向电流密度()作比较从而初步确定该方法对涡流场优化的程度.表3 列出了以上电流密度比较与原点处电势的模拟结果.

表3 数值模拟结果Table 3.List of numerical simulation results.

图11 原始及3 种优化设置涡电流场电流密度分布Fig.11.Eddy current field current density distribution of original and three optimized patterns.

图11(b)为聚Y方向电流设置下的涡电流场,电流密度分布图中的红色区域可视为该设置下的ESZ 区域,其区域面积约为原始设置ESZ 面积的1/8,且原点处电流密度在Y方向的分量比原始设置情况下提高了38%.此外,其电流密度分布图中主要由3 条主要的电流组成,中间的、经过原点的电流主要方向平行于Y轴正半轴;两侧的电流主要方向与之相反,电流密度也远不及中间电流.聚Y方向电流设置的优点在于抑制了永磁体各单元产生的涡电流在原点处Y方向分量相互抵消的作用,从而有力提高了原点处Y方向的电流密度.

图11(c)为聚X方向电流设置下的涡电流场,电流密度分布图中的红色区域可视为该设置下的ESZ 区域,其区域的面积约为原始设置ESZ 面积的1/10.且原点处电流密度在X方向的分量比原始设置情况下提高了54%.聚X方向电流设置的优点在于抑制了永磁体各单元产生的涡电流在原点处X方向分量相互抵消的作用,从而有力提高了原点处X方向的电流密度.

从图12 也可观察到,当不同表面剩余磁通方向永磁体部分的边界与相对速度平行时,便会在导电板中与该边界对于的位置形成至少一个电势极点.聚X方向电流设置具有两个表面剩余磁通方向相反的边界与相对速度方向平行,故其形成两个电势极点,并在电势极点之间形成了ESZ.

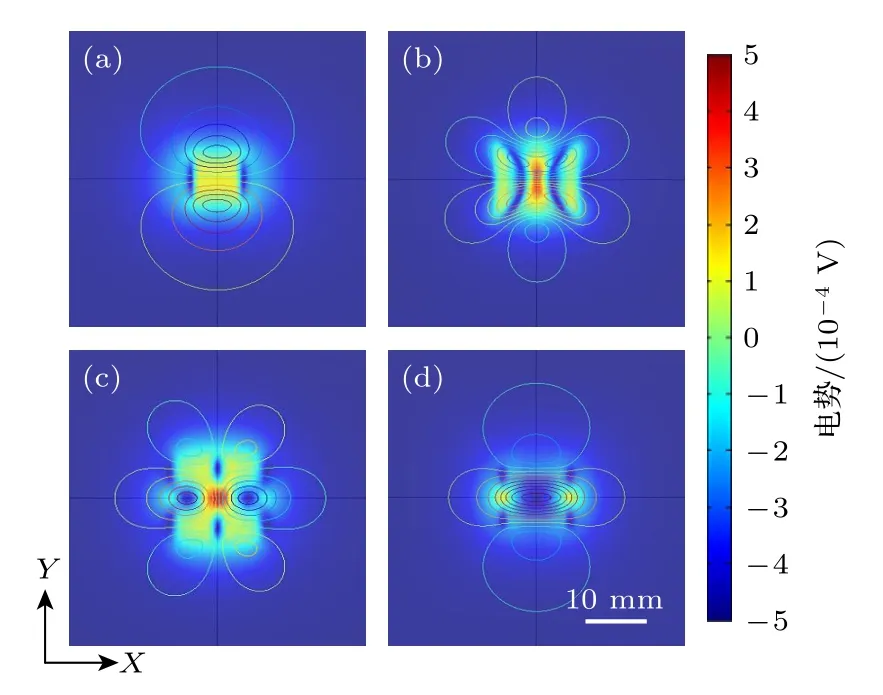
图12 原始及3 种优化设置涡电流场等势线分布Fig.12.Equipotential distribution of eddy current field in the original and three optimized patterns.

图11(d)为聚集电势设置下的涡电流场.很明显,聚集电势设置中只存在一个平行于相对速度方向的剩余磁通方向相反边界.故其只在原点处形成一个电势极点,但理论上电势极点处的电流密度模为零.则当缺陷接近电势极点时,缺陷对运动感应涡流的影响可忽略不计.因而缺陷运动过程中,只在电势极点旁的两个ESZ 中对运动感应涡流具有较明显的影响.在每个ESZ 中,电流密度主要平行于X方向,且电流密度在X方向的分量略小于原始设置.

2.5 缺陷信号取决于第一磁场设置

根据2.3 节的结论,由于原始设置的第二磁场磁通变化量的X方向分量明显大于Y方向分量,因而取缺陷信号标表示为.聚Y方向电流设置的第二磁场磁通变化量的X方向分量明显大于Y方向分量,因而取缺陷信号表示为.聚X方向电流设置的第二磁场磁通变化量的Y方向分量明显大于X方向分量,因而取缺陷信号标表示为.模拟结果如图13 所示.表4 给出了该模拟结构的尺寸与位置参数.

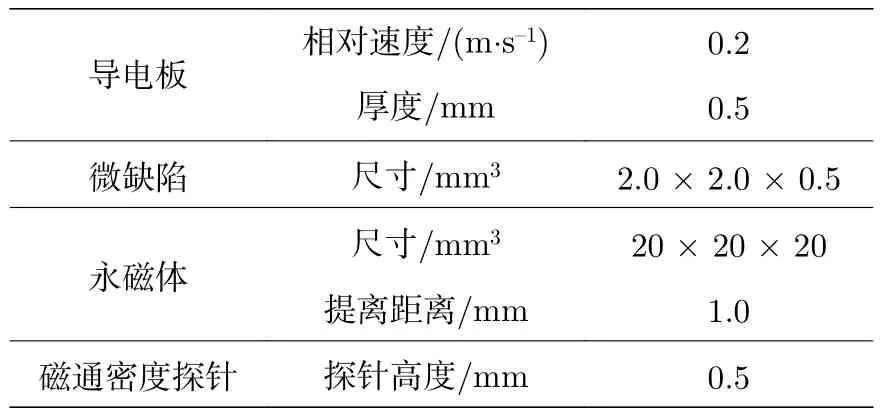
表4 模拟部分参数Table 4.Parameter of simulation part.

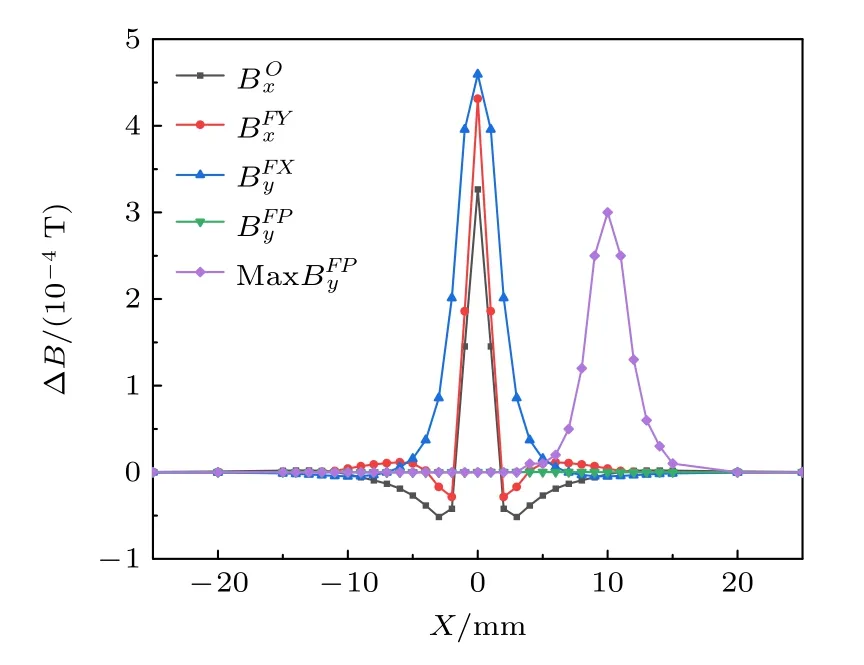
图13 各永磁体设置下的缺陷信号Fig.13.Defect signal at each permanent magnet patterns.

与2.4.2 节推测的结果基本一致,由于聚X和聚Y方向电流设置下的涡电流场在原点处的电流密度模大于原始设置,聚X和聚Y方向电流设置产生的缺陷信号大于原始设置.其中相较于原始设置下的缺陷信号幅值,聚Y方向电流设置将幅值提高到132%,聚X方向电流设置将幅值提高到141%.考虑图11 中,聚集电势设置下的ESZ 不在电势极点附近,而是处于永磁体投影轮廓线上.故对于聚集电势设置下的缺陷信号需要分别在两个检测点处获得并对比:P原点正上方;Q坐标点(10,0,0)处的正上方.两检测点距导电板表面的距离均为0.5 mm.

在检测点P处,聚集电势设置情况第二磁场磁通变化量的X与Y方向分量都较小,故采用Y方向分量,取缺陷信号标表示为.由图13可以看出,聚集电势设置下的检测点P处第二磁场基本不变化,这也证明了该设置产生的运动感应涡电流在原点附近确实具有很高的稳定性.在检测点Q处,ESZ 中电流密度主要为X方向,因而该点处的第二磁场磁通变化量的Y方向分量明显大于X方向分量.因而取缺陷信号表示为Max.聚集电势设置将幅值降低到92%.这与Rocha 等[19]的实验结果基本一致.考虑缺陷脉宽的不同可以观察到,聚Y方向电流设置并没有明显使缺陷信号脉宽产生变化,而聚X方向电流设置与聚集电势设置却使得缺陷信号的脉宽增大.这是由于聚X方向电流设置的ESZ 中的电流方向与缺陷运动轨迹相平行所致.

3 实验方法

缺陷信号依赖于ESZ 的实验结构和模拟部分2.3 节相似.同时为消除多永磁体之间由于退磁水平不同引入的误差,实验部分使用一个原始永磁体来代替模拟中的一组.为了减少振动对信号测量产生的噪声,实验的导电板采用旋转的运动方式.实验中缺陷距离圆盘边缘较近,主要考虑到在越是边缘的区域其运动方式就越接近平动.实际测量时,永磁体下方被圆盘完全覆盖,即ESZ 并未达到边缘.从文献[20]与本文逻辑的角度,边缘效应会存在部分影响,但在图11 可以看到,在导体上磁体正下方以外的区域,其感应涡电流相比于磁体正下方区域很弱且衰减较快.因此可以认为这种影响是可忽略的.导电板内存在微缺陷(其直径为D),不同尺寸缺陷的中心距离导电板圆心距离均为55 mm(忽略加工误差).导电板转速为37 r/min,缺陷位置速度为0.2 m/s.

表5 列出了本部分对应的实验参数.由于小尺寸永磁体在实验中难以准确控制其相对位置,故采用a=5,10,20 mm 的永磁体.实验中使用的传感器为通用多功能线性TMR 传感器(多维科技公司,TMR2104),该传感器具有较高的灵敏度(3.1 mV·V–1·Oe–1),其可将所在处的磁通密度变化(第二磁场变化)表示为输出电压V变化.

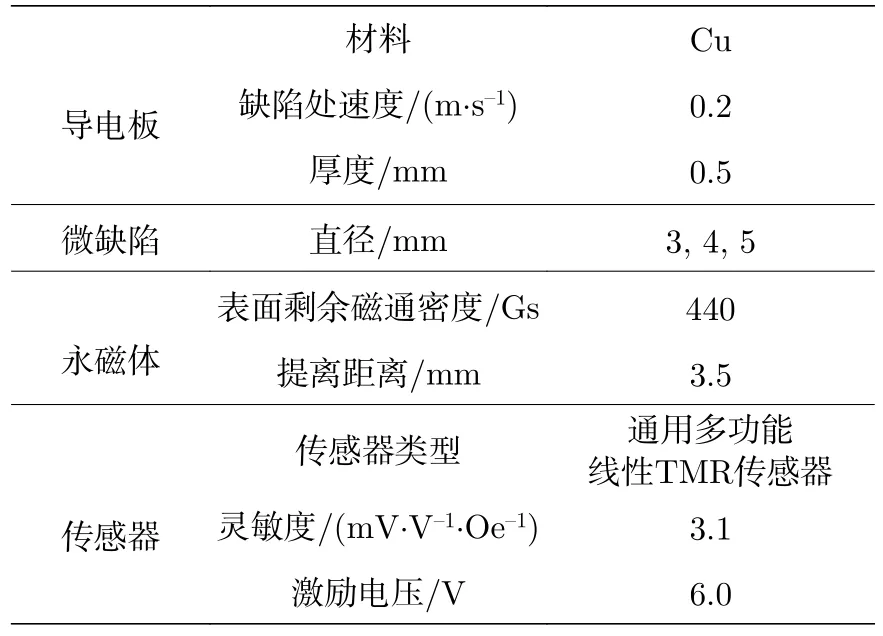
表5 实验参数Table 5.List of experimental parameters.

缺陷信号取决于永磁体设置的实验结构与上文相同,如图14 所示.实验所用的传感器贴附于永磁体上表面,处于旋转铜盘与永磁体之间.实验控制变量仅为永磁体结构,如图15 所示,3 种设置的永磁体尺寸均为20 mm.分别测量了原始设置、聚Y方向电流设置与聚X方向电流设置三类永磁体下,铜盘中缺陷所产生的第二磁场信号.

图14 实验结构Fig.14.Experimental structure.

图15 三种永磁体设置Fig.15.Three permanent magnet settings.

4 结果与讨论

4.1 缺陷信号依赖于ESZ

缺陷信号依赖于ESZ 的实验结果如图16 所示.实验与模拟结果在变化趋势上具有较好的一致性.增大永磁体尺寸可以提高运动感应涡流缺陷信号的幅值.a=10 mm 相比a=5 mm 的永磁体,信号幅值提高55%—82%.a=20 mm 相比a=5 mm 的永磁体,信号幅值提高105%—123%.并且随a的增大,缺陷信号增长率变小,这也与模拟呈现的趋势相同.实验与模拟部分缺陷信号的脉宽方面存在一定差别.原因可能有: 1)模拟与实验部分的缺陷形状不相同.即模拟的边界条件与实验存在部分差别,相应的缺陷信号幅值存在差异.2)实验中,转动的导电板不是绝对水平,因而会是提离距离发生微小变化.

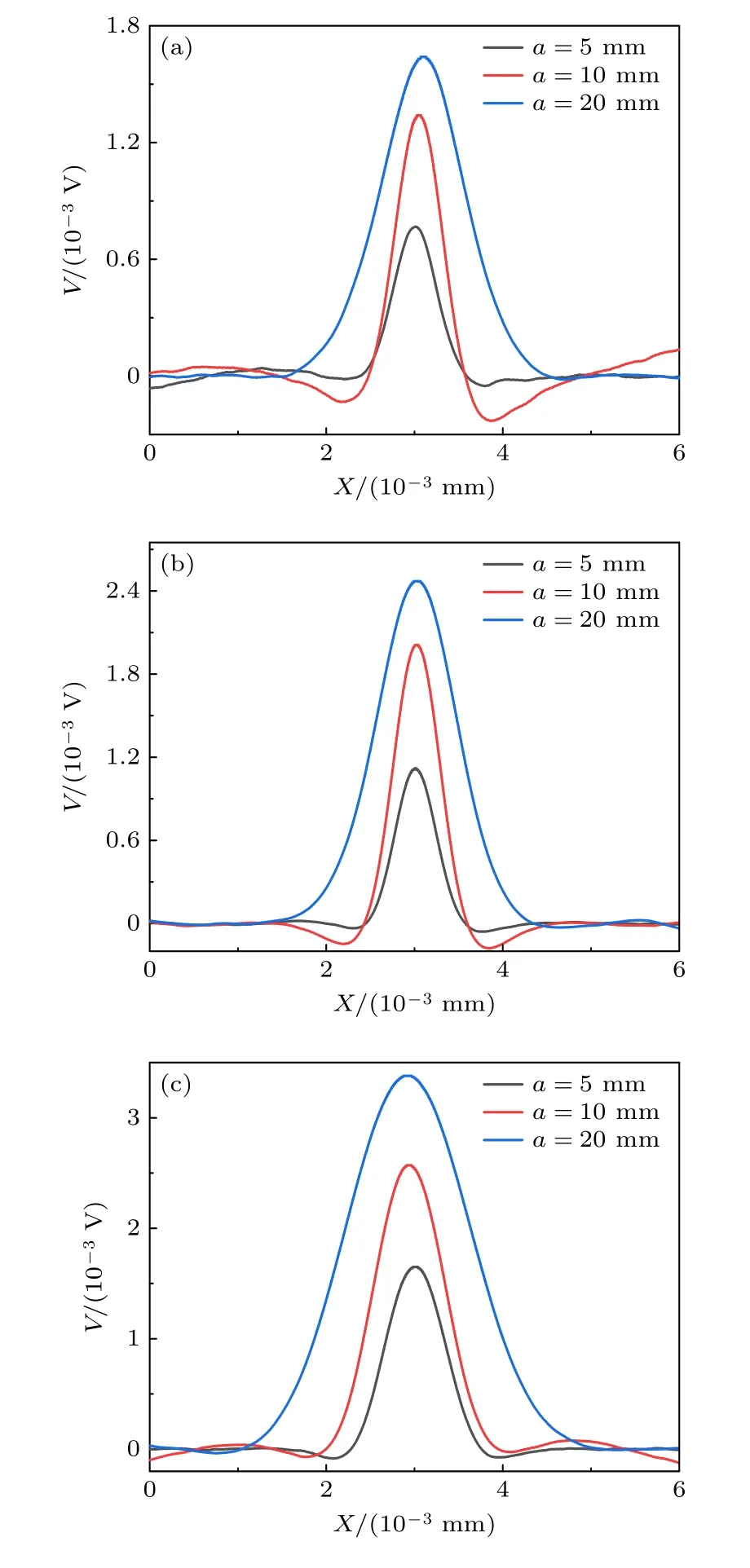
图16 改变永磁体尺寸对缺陷信号的影响 (a) D=3 mm;(b) D=4 mm;(c) D=5 mmFig.16.Effect of changing permanent magnet size on defect signal: (a) D=3 mm;(b) D=4 mm;(c) D=5 mm.

4.2 缺陷信号取决于第一磁场设置

缺陷信号取决于第一磁场设置的实验结果如图17 所示.实验与模拟结果在变化趋势上具有较好的一致性.聚Y方向电流设置与聚X方向电流设置相对于原始设置,可以提高运动感应涡流缺陷信号的幅值: 聚Y方向电流设置下,信号幅值提高78%—91%;聚X方向电流设置下,信号幅值提高88%—92%.且聚X方向电流设置的缺陷信号幅值与脉宽,都略大于聚Y方向电流设置,这与模拟结果相符.两种优化后的第一磁场设置具有的信号提升比率相当.模拟中聚X方向电流设置比聚Y方向电流设置略大的结果,在实验中由于存在部分误差所以并不明显.

图17 聚Y 方向电流设置与聚X 方向电流设置下的缺陷信号 (a) D=3 mm;(b) D=4 mm;(c) D=5 mmFig.17.Defect signal under current patterns of poly Y direction and poly X direction: (a) D=3 mm;(b) D=4 mm;(c) D=5 mm.

实验与模拟部分信号提升率存在一定差别,原因可能有以下3 点: 1)模拟部分的探针点处于空气域中,该部分的网格划分程度会带来一定误差.2)模拟与实验部分的缺陷形状不相同.这可能导致涡电流畸变程度不同,则相应的缺陷信号幅值存在差异.3)实验中,转动的导电板不是绝对水平,因而提离距离会发生微小变化.

5 结论

根据经典电磁学理论,提出一些MIECMF 方法的优化方法.根据模拟计算的假设,从最简单的单一磁体开始,探究磁体尺寸和涡电流及ESZ 的关系,进而模拟出不同永磁体尺寸下的缺陷信号.由此得到结论: 当永磁体尺寸约达到提离距离的10 倍之后,继续增大永磁体尺寸,原点处电流密度模不再有明显增长.在提离距离、相对运动速度与传感器位置等条件确定时,缺陷信号的幅值仅由ESZ 中原始电流密度在Y方向的分量决定.

基于这个结论,在永磁体尺寸外探索第一磁场设置方式优化的可能.通过研究永磁体微元在原点处的贡献得出不同的第一磁场设置方式,进而比较各设置方式下产生的涡电流与缺陷信号.本文提出一种MIECMF 中第一磁场的优化方法.由该方法产生的两种永磁体阵列,相比于同体积、同表面剩磁的简单永磁体在固定相对运动速度,提离距离的前提下,提高了感应涡电流的强度,从而提高缺陷第二磁场检测信号.提出了聚Y方向电流、聚X方向电流和聚集电势的3 种永磁体设置方法,其中聚Y方向电流、聚X方向电流设置对缺陷信号的幅值都有所提升,从而提高MIECMF 方法对于微缺陷的检测能力.