金刚石/环氧树脂复合物热导率的分子动力学模拟*

刘秀成 杨智† 郭浩 陈颖 罗向龙 陈健勇

1) (广东工业大学材料与能源学院,广州 510006)

2) (中国科学院理化技术研究所,低温工程学重点实验室,北京 100190)

提高环氧树脂热界面材料热导率对解决5G 等微电子芯片高热流密度散热问题具有重要意义.采用非平衡态分子动力学方法,重点研究了纳米金刚石填料的不同填充方式对环氧树脂基复合物热导率的影响.结果表明,单颗粒填充方式下,复合物热导率随金刚石尺寸的增大而增大,大尺寸金刚石填料可以降低复合物的自由体积分数,对热导率的提升效果更显著;多颗粒填充方式下,复合物热导率随颗粒数的增多呈先增大后减小的趋势,增加颗粒数可以减小复合物的自由体积分数,但具有更大的比表面积及界面热阻,其对热导率的削弱作用更为显著.此外,同一质量分数下,增大纳米金刚石颗粒尺寸比增加颗粒数对复合物热导率的提升效果更为显著.本文研究对具有高热导率的纳米金刚石/环氧树脂复合物热界面材料的设计和制备具有指导意义.

1 引言

随着新一代5G 通讯技术的不断发展和芯片制造工艺的不断进步,核心电子器件日趋高功率和高集成化,高热流密度的散热问题成为制约微电子器件进一步发展的瓶颈.环氧树脂作为一种典型的热固性聚合物,具有良好的热稳定性、化学稳定性、机械性能、电绝缘性和黏结性等,被广泛应用于热界面材料和电子封装等领域[1−3].然而,环氧树脂的热导率通常很低(0.1—0.3 W·m–1·K–1)[4,5],难以满足高功率和高集成化的核心电子器件的散热需求.为提高环氧树脂的热导率,最常用的方法是添加高导热填料以形成聚合物复合物.常用填料主要包括金属及其化合物[6]、氮化硼[7]、石墨烯[8,9]、碳纳米管[10,11]和金刚石[12]等.其中,金属及其化合物和氮化硼填料的本征热导率不高,而具有高热导率的石墨烯和碳纳米管等碳基填料则具有较大的电导率,不宜作为芯片等电子器件直接接触的导热材料[7].

金刚石具有高热导率(2000 W·m–1·K–1)、低电导性(1000 Ω·cm)、极高的硬度和电化学性能稳定等优异性能,且可实现纳米尺度的加工与制备[13],已成为一种重要的聚合物热导率强化填料.近年来,以金刚石为填料强化聚合物热导率的研究受到了广泛关注.Cho 等[14]实验研究了金刚石/聚硅氧烷复合物,发现金刚石颗粒填料呈线性排列时可使复合物热导率提升至0.301 W·m–1·K–1.Sun 等[15]实验制备了金刚石/硅酮复合物,发现金刚石薄层呈平行分层分布时,复合物热导率达到2.0 W·m–1·K–1,比相同填充质量分数下的随机填充形式提高了335%.Kang 等[13]将金刚石颗粒填充于聚氨酯聚合物中,并获得了0.434 W·m–1·K–1的复合物导热率.Neitzel 等[16]将纳米金刚石填充于环氧树脂中,并获得0.32 W·m–1·K–1的复合物导热率,而纯环氧树脂热导率仅为0.25 W·m–1·K–1.综上所述,金刚石作为高导热填料对聚合物导热性能提升效果显著.然而,当前以金刚石为填料的复合物导热性能研究仍以实验为主,且金刚石填料对环氧树脂等热界面材料导热特性的影响规律及内在机理研究仍较为缺乏,如将多少颗粒数或者多大尺寸的金刚石颗粒添加到环氧树脂才能更有效提升复合物的热导率,这个问题至今仍未被深入研究和认识.

分子动力学(molecular dynamic,MD)[17]作为一种常用的微观分析手段,在预测物质宏观性质上具有较高的准确性,已广泛用于复合物微观热传导特性及机理的研究.Yang 等[18]采用MD 方法,模拟计算了石墨烯纳米片/环氧树脂复合物的导热性能,并获得了与实验较好的一致性.Zhu 等[19]采用MD 研究了氮化硼填料对环氧树脂导热性能的影响,且通过声子态密度分析进一步阐明了氮化硼/环氧树脂复合物的导热机理.因此,本文同样采用MD 方法,开展金刚石/环氧树脂复合物的热导率研究,进而阐明金刚石颗粒尺寸和颗粒数对金刚石/环氧树脂复合物热导率的影响规律及其微观机理,这对采用何种填充方式来高效提升金刚石/环氧树脂复合物热导率具有重要的指导意义.

2 模型构建与计算方法

2.1 单体分子模型

分别选用双酚F 二缩水甘油醚(di-glycidyl ether of bisphenol F,DGEBF)和二乙基甲苯二胺(diethylene toluene diamine,DETDA)作为环氧树脂单体和交联剂,金刚石颗粒作为填充材料,其分子结构如图1(a)所示.所有单体结构模型均在Materials Studio 2019 (MS)软件中构建.每个环氧单体分子上有两个环氧官能团,每个交联剂分子有两个氨基官能团.一个氨基官能团可以与两个环氧官能团反应,因此DGEBF 和DETDA 的混合比例通常为2∶1.

2.2 环氧树脂交联模型

对环氧树脂单体DGEBF 和交联剂DETDA分子分别进行结构优化后,将64 个DGEBF 和32 个DETDA 分子填充到周期性盒子中,构建DGEBF/DETDA 非晶模型,如图1(d)所示,模拟盒子的尺寸、初始密度和温度分别为33.72 Å×33.72 Å×33.72 Å (1 Å=10–10m),1.1 g/cm3和300 K.在构建非晶模型的过程中,采用Smart Minimizer 算法对模型进行结构优化,使模型能量达到最小化.随后将初始构型在温度为300 K 的等温-等容系综(NVT)下弛豫100 ps,继而在压力为1.01×105Pa 的等温-等压系综(NPT)下弛豫100 ps,主要用于获得适当的非晶模型密度和降低内应力.温度和压力分别由Andersen 温控器和Berendsen 调压器控制,时间步长为1 fs.

交联反应的流程如图1(c)所示.在交联过程中,DETDA 中的氨基与DGEBF 中的环氧基发生反应,当氨基中氮原子和环氧基中碳原子之间的距离小于反应截断距离时,环氧基末端的碳氧键断开,氨基的氮与环氧基末端的碳之间进行成键,环氧基中的氧原子与氨基脱落的氢原子形成羟基(—OH).为避免交联反应中新生成的键产生过大应力,体系随后在NPT 系综下弛豫50 ps,然后再进行新一轮的交联反应,直到达到最大截断距离或达到设定的交联率,交联程序运算完成.交联后的模型结构见图1(e).交联过程温度设为600 K,最大截断距离设为10 Å.在理想的条件下充分反应时,交联率可达到100%,但实际体系的交联率一般在80%—95%内[20].因此,本文选取环氧树脂交联率为90%.

2.3 复合物模型

为构建金刚石/环氧树脂复合物模型,采用Amorphous Cell 模块将不同质量分数的金刚石纳米颗粒混入环氧树脂基质中,并采用Smart 算法进行多次几何优化,直到复合模型体系能量趋于稳定.随后模型在NPT 系综下弛豫100 ps,直到密度和能量充分收敛.在此过程中,时间步长设置为l fs,采用Nose-Hoover 调温器和Berendsen 调压器将体系温度和压力分布控制在T=300 K 和P=1.01×105Pa,模拟盒子设置为周期边界条件.此外,为保证模拟体系的电中性,本文将纳米金刚石颗粒表面带有自由基的碳原子进行加氢处理,过程如下: 1) 从MS 案例库中导入金刚石晶格结构;2) 使用Build Nanocluster 工具构建不同粒径的纳米颗粒;3) 使用Adjust hydrogen 模块对纳米金刚石颗粒表面带有自由基的碳原子进行加氢处理.

2.4 热导率计算方法

热导率计算的分子模拟方法主要包括平衡态分子动力学(equilibrium molecular dynamic,EMD)和非平衡态分子动力学(non-equilibrium molecular dynamic,NEMD).尽管EMD 方法受尺寸效应影响较小[21],但其计算值波动性大,通常需要独立计算多次取平均,计算成本较高.然而,NEMD 方法计算结果稳定准确,且收敛速度快[22,23].NEMD 产生温度梯度的方法主要有动量交换法、速度重标法和局部热浴法[22,24,25],其中动量交换法里的能量交换频率和速度重标法中的能量值均需要用试错法来确定.相比之下,在局部热浴法中可以直接设定热源和热汇的温度值,从而保证具有合理的温度梯度值.事实上,在纳米复合物等非均质体系中,热源和热汇之间原子速度的交换可能会涉及不同相的原子(如石墨烯和环氧树脂),它们的特征是不同的振动模式,可能导致整个计算域的热流不均匀,从而产生偏差结果.因此,采用基于局部热浴法的NEMD 方法来计算热导率,计算原理如图2(a)所示.将模拟盒子分成20 等份,第1 层温度设定为330 K,中间层温度设定为270 K,通过郎之万控温方法在冷热层间构建温差,当体系达到稳定后进行温度梯度和冷热端热流的统计计算,进而通过傅里叶公式计算热导率.在NEMD 模拟中,首先将模型依次在300 K 和1.01×105Pa 的NPT 系综和300 K 的NVT 系综下弛豫500 ps,随后在NVE系综下弛豫500 ps 以建立稳定的温度梯度.最后,继续进行2500 ps 的平衡计算,并通过采样统计平衡体系的热流和温度梯度,体系冷热端的吸放热量和温度分布如图2(b)和图2(c)所示.模拟时间步长设置为0.25 fs,三个方向均设为周期性边界条件,采用PCFF 力场[2,26,27]描述环氧树脂内原子间的相互作用,采用Tersoff 势函数[18]描述金刚石原子间的相互作用,采用Lennard-Jones 12-6 势(如(1)式)描述环氧树脂与金刚石颗粒之间的相互作用,这些力场均已被广泛用于复合物体系的分子模拟研究[18].本文中,所有NEMD 计算均在LAMMPS平台下进行,金刚石/环氧树脂复合物热导率的分子模拟计算流程如图1(b)所示.

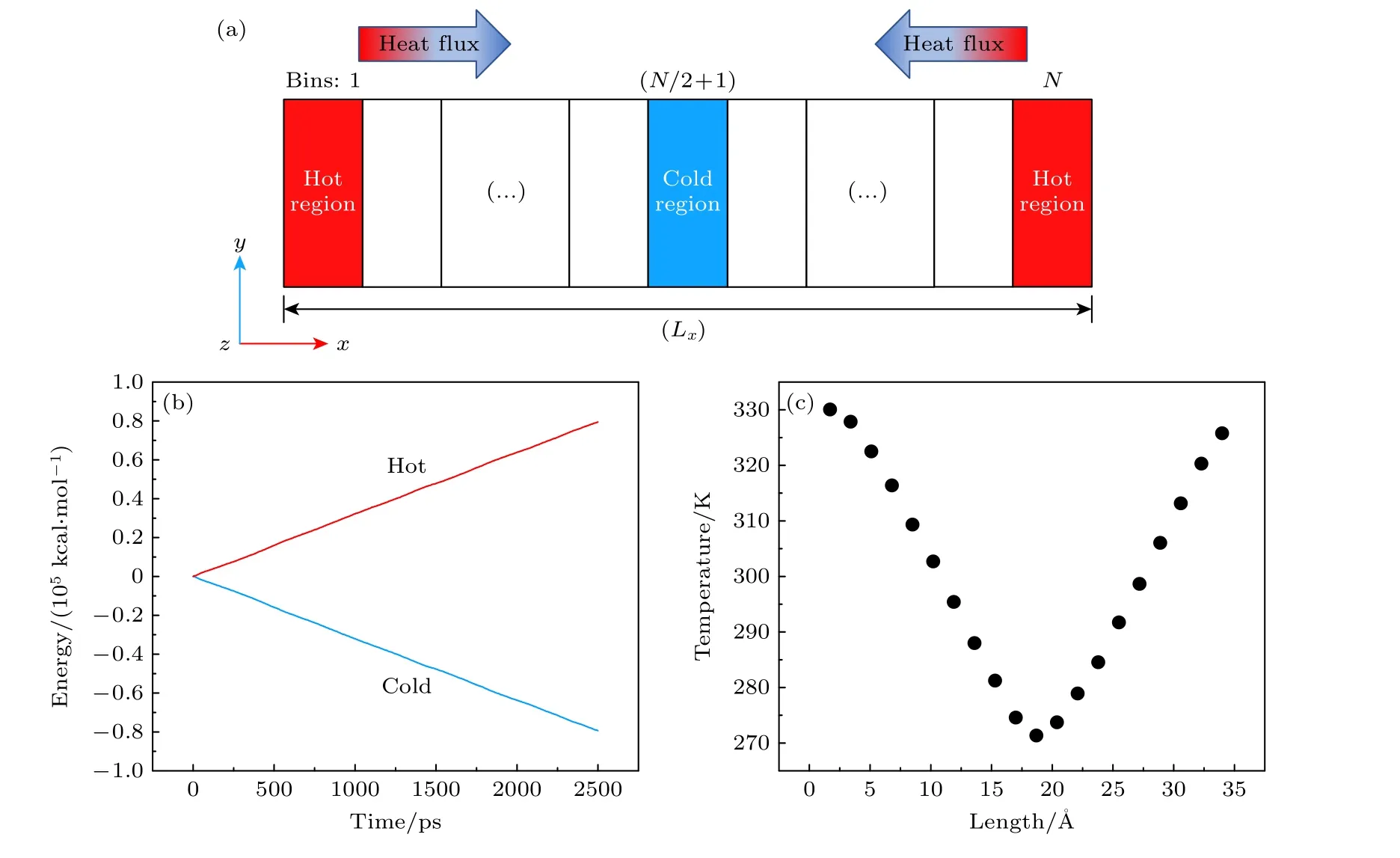
图2 (a) 热传导方向示意图;(b) 冷热端的能量变化;(c) 环氧树脂在x 方向上的温度分布Fig.2.(a) Schematic diagram of heat conduction direction;(b) energy change in hot and cold regions;(c) temperature distribution in the x direction of the epoxy resin.

式中,rij是粒子i和粒子j之间的距离;ε和σ分别代表分子能量和尺寸参数,不同原子类型之间的势参数可通过洛伦兹混合法则计算得出:

3 结果与讨论

3.1 交联率对环氧树脂热导率的影响

环氧树脂一般由环氧树脂单体和交联剂交联聚合而成,这与聚乙烯等线性聚合物有着显著差异.现有研究表明,交联率对环氧树脂热导率可产生不同的影响,如Li 等[28]和Huo 等[29]研究表明交联率对环氧树脂热导率的影响极为微弱,而Wan 等[30],Liu 等[31]以及Xu 等[32]研究表明环氧树脂热导率随着交联率的增大而增大.因此,针对以上研究分歧,首先研究了交联率对环氧树脂热导率的影响.取交联率分别为0%,18.75%,32.81%,49.22%,64.06%,75.78%,90.00%的体系作为计算模型,部分模型结构如图3 所示,其中球棍模型表示参与交联反应的交联点,线状模型表示体系中的其他原子.

图3 不同交联率的模型结构 (a) 0%;(b) 32.81%;(c) 64.06%;(d) 90.00%Fig.3.Model structures with different cross-linking rates:(a) 0%;(b) 32.81%;(c) 64.06%;(d) 90.00%.

图4 给出了环氧树脂热导率预测值与交联率的函数关系.结果表明,环氧树脂热导率随着交联率的增大而增大,与Wan 等[30]和Liu 与Rao[31]的模拟结论一致.当交联率为90.00%时,环氧树脂的热导率可达0.23 W·m–1·K–1,比未交联体系提升了77%.可见,交联率对环氧树脂热导率具有显著影响,这主要由于分子体系中的键连接在传热过程的贡献比重增大,即更多交联键的引入为传热开辟了新的途径,并直接强化热输运[33,34].此外,实验测定的环氧树脂热导率通常在0.1—0.3 W·m–1·K–1之间,这与本文的模拟预测值具有较好的一致性,也表明本文所选取的分子力场及模拟计算方法的可靠性.

图4 环氧树脂热导率与交联率的函数关系Fig.4.Functional relationship between thermal conductivity and cross-linking rate of epoxy resin.

3.2 金刚石质量分数对复合物热导率的影响

通常,填料质量分数对复合物热导率具有显著影响.然而,填料的不同添加形式也会引起复合物热导率的差异,将多少颗粒数或多大尺寸的金刚石颗粒添加到环氧树脂才能更有效提升复合物的热导率,这个问题至今仍未被深入研究和认识.为此,采用变金刚石粒径和金刚石颗粒数这两种方式分别来改变填料质量分数,进而研究这两种方式对金刚石/环氧树脂复合物热导率的影响.

3.2.1 填料粒径对热导率的影响

为研究填料粒径对复合物热导率的影响,选取6 种尺寸金刚石颗粒 (分别为1,1.2,1.4,1.6,1.8和2 nm),进而将不同尺寸的颗粒掺混至环氧树脂中进行复合物热导率的研究,部分复合物模型如图5(a)所示.复合物热导率随金刚石质量分数(颗粒尺寸)变化的关系如图5(b)所示,复合物热导率随金刚石质量分数的增大而增大,当金刚石质量分数为26.15%时,热导率可达0.592 W·m–1·K–1,是纯环氧树脂的2.52 倍.由此可见,大尺寸的金刚石颗粒填料相比小尺寸能更有效提高复合物热导率.为了从微观结构上揭示纳米金刚石填料对复合物热导率的影响,图5(c)给出了不同复合物体系的径向分布函数(radical distribution function,RDF).计算结果表明,不同复合物体系的RDF 曲线均具有较好的相似性,其主要峰的峰值均位于1.11 Å和1.41 Å,金刚石颗粒尺寸越大,RDF 的峰值越小,表明随着金刚石体积分数占比增大,环氧树脂分子的自由运动逐渐受到限制,导致复合物体系中氢原子和碳原子周围出现其他原子的概率逐渐减小,进而减小声子散射.从图6 和表1 可知,随着金刚石粒径的增大,复合物的自由体积分数(fractional free volume,FFV)逐渐减小,同样表明大尺寸颗粒更严重挤压了环氧树脂的自由运动空间,与RDF结果一致.

表1 不同粒径复合物的自由体积Table 1.Free volumes of composites with different particle sizes.

图5 不同粒径复合物 (a) 结构图;(b) 热导率;(c) 径向分布函数Fig.5.Different particle size composites: (a) Structure diagram;(b) thermal conductivity;(c) radial distribution function.

3.2.2 填料颗粒数对热导率的影响

复合物热导率不仅取决于颗粒粒径,还与其在基体材料中填料的数量有关[35,36].为研究金刚石颗粒填料数量对复合物热导率的影响,本文选取的颗粒数分别为1,2,3,4,6,10,其中颗粒尺寸均为1 nm,并与环氧树脂掺混形成不同的复合物体系,部分复合物体系模型如图7(a)所示.

图7 不同颗粒数复合物 (a) 结构图;(b) 热导率;(c) 振动态密度图谱Fig.7.Composites with different particle numbers: (a) Structure diagram;(b) thermal conductivity;(c) vibrational density of state.

之前,Neitzel 等[16]实验研究了纳米金刚石填料不同体积分数对环氧树脂基复合物热导率的影响,结果显示当体积分数由0%增大至12%时,复合物热导率几乎不变或变化很小,并将其原因简单归结为纳米颗粒在体相空间的均匀分散特性,但未提供纳米颗粒微观分散特性的实验表征结果.为获得更清晰的微观机理认识,进而采用MD 方法开展了多颗粒填充的金刚石/环氧树脂基复合材料热导率的影响,发现在0%—13.35%的体积分数填充范围内,其所对应的填充颗粒数为0—10,对应的质量分数为0%—30.38%,复合物的热导率呈现出先增加后减小的变化规律,如图7(b)所示.单颗粒填充下,复合物的热导率显著增大至0.393 W·m–1·K–1,比纯环氧树脂提高67%;当颗粒数由1 增大至4时,复合物热导率变化极小;值得注意的是,随着填充颗粒数的继续增多,复合物热导率的变化呈下降趋势,其主要原因为填充于环氧树脂中的颗粒处于随机分散状态,随着颗粒数的持续增多,复合物中纳米颗粒的比表面积更大,从而产生较大的界面热阻.如表2 所列,金刚石颗粒数的增多同样导致复合物自由体积分数的减小,这与颗粒尺寸增大的效果一致,也即自由体积分数减小实质上可强化复合物热导率.然而,单颗粒添加形式具有较为通畅的热输运路径,而多颗粒的掺混不仅增大了复合物体系的界面热阻,还会形成多个局部热点,在内部形成了复杂的导热网络及无效的传热路径.

表2 不同颗粒数复合物的自由体积Table 2.Free volumes of composites with different particle numbers.

根据理论模型(即声学失配模型和扩散失配模型)可知,两种界面材料振动态密度(vibrational density of state,VDOS)的匹配程度在本质上决定了其界面间的热输运[37-39].因此,为了阐明多颗粒填充形式对复合物热导率的影响机制,计算并对比了纯环氧树脂和不同复合物体系的振动态密度.如图7(c)所示,环氧树脂的VDOS 曲线一般是宽频低频峰,这可归因于是由环氧树脂结构的无定型性质决定的[40],可用于解释环氧树脂热导率低的性质.当填充颗粒数从2 增加到4 时,复合物VDOS曲线与纯环氧树脂VDOS 曲线的匹配现象得到改善,故热导率得到提升.随着填充颗粒数的进一步增多,复合物VDOS 曲线逐渐偏离纯环氧树脂的VDOS 曲线,意味着界面不匹配现象愈加严重,也即体系的界面热阻逐渐增大,从而导致复合物的热导率变小.

3.3 单颗粒和双颗粒填充对复合物热导率的影响

为进一步研究相同颗粒质量分数下单颗粒和多颗粒填充对复合物热导率的影响区别,进一步构建了质量分数分别为7.84%,11.92%,20.91%和26.15%的单颗粒和双颗粒复合物体系,并计算了不同复合物体系的热导率,结果如图8 所示.对比结果可知,所有质量分数下单颗粒金刚石填充的复合物热导率均大于双颗粒填充的复合物.当填充颗粒质量分数为20.91%时,单颗粒复合物的热导率为0.54 W·m–1·K–1,比双颗粒复合物热导率高出29.59%.显然,双颗粒在复合物体系具有更大的界面热阻,且未形成有效的导热网络,故在相同填充质量分数下,颗粒尺寸相比于颗粒数对复合物热导率的提升效果更为显著.

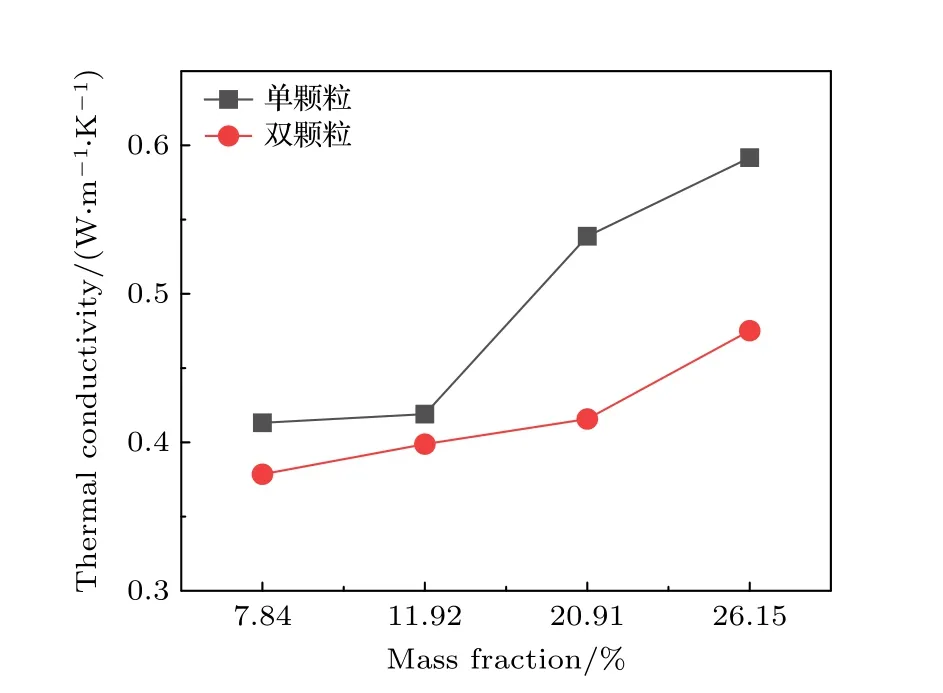
图8 不同质量分数复合物的热导率Fig.8.Thermal conductivity of composites with different mass fractions.

4 结论

提高环氧树脂热界面材料热导率对解决微电子芯片高热流密度散热问题具有重要意义.金刚石颗粒作为一种高导热填料,对环氧树脂热导率具有潜在的强化效果.因此,本文主要开展了纳米金刚石/环氧树脂复合物热导率的MD 模拟研究,旨在探究纳米颗粒的不同填充形式对复合物热导率的影响规律,主要结论如下.

1) 不同交联率下环氧树脂热导率模拟结果与实验值具有较好的一致性,且环氧树脂热导率随交联率的增大而增大.这主要由于更多交联键的引入为传热开辟了新的途径,从而提高了整体的热导率.

2) 在单颗粒填充方式下,复合物热导率随金刚石颗粒尺寸的增大而增大,当填充质量分数为26.15%(颗粒尺寸2 nm)时,复合物热导率可达0.592 W·m–1·K–1,是纯环氧树脂的2.52 倍.这主要是由于大尺寸颗粒复合物的自由体积分数更小,进而减少了声子散射.

3) 在多颗粒均一粒径填充方式下,复合物热导率随金刚石颗粒数的增多呈先增大后减小的变化趋势.尽管颗粒数增多同样使得复合物自由体积分数减小,复合物热导率提高,但颗粒数过多会使得纳米颗粒的比表面积增大,界面热阻显著增大,其对热输运的削弱作用远大于自由体积分数减小对热导率的提升效果,从而导致复合物热导率下降.

4) 同一填料质量分数下,单颗粒填充的复合物热导率比双颗粒填充具有更高热导率,双颗粒填充并不能形成更有效导热网络,反而增大了界面热阻.因此,颗粒尺寸相比于颗粒数对复合物热导率的提升效果更为显著.