超冷原子动量光晶格中的非线性拓扑泵浦*

苑涛 戴汉宁† 陈宇翱

1) (中国科学技术大学,合肥微尺度物质科学国家研究中心和物理学院,合肥 230026)

2) (中国科学技术大学,上海量子科学研究中心和中国科学院量子信息与量子科技创新研究院,上海 201315)

3) (合肥国家实验室,合肥 230088)

在拓扑系统中,探索相互作用引起的新奇的拓扑泵浦现象日益受到人们的关注,其中包括由相互作用诱导的非线性拓扑泵浦.本文提出可以利用超冷原子动量光晶格系统,有效地模拟一维非线性的非对角Aubry-André-Harper (AAH) 模型,研究非线性拓扑泵浦的实验方案.首先,通过数值方法计算了一维非对角AAH模型的非线性能带结构随相互作用强度的变化,得到了非线性系统的孤子态解.然后,分析了不同相互作用强度下孤子态的拓扑输运,发现其质心的移动距离具有量子化的输运特征,由所占据能带的陈数决定,并讨论了非线性拓扑泵浦对相互作用符号的依赖性.同时还计算了在不同相互作用强度下,系统最低能带和最高能带对应陈数的分布.最后,基于 7 Li 原子的动量光晶格实验系统,提出了一个非线性拓扑泵浦方案.本文构造了一种近似于孤子态分布的初始态并演示了其动力学演化过程,并分析了绝热演化条件对泵浦过程的影响.结果表明,在动量晶格系统中演示非线性拓扑泵浦具有可行性.本文的工作为在超冷原子系统中研究非线性拓扑泵浦提供了一个可行的途径,有助于进一步探测非线性引起的拓扑相变和边界效应.

1 引言

拓扑泵浦[1]是一种在绝热调制的周期性势阱中的量子化输运现象,在实现粒子的量子化传输[2]、纠缠态产生[3]和探索高维拓扑系统性质[4]方面有重要的应用.因此,人们对其进行了大量的研究[5−7],并在超冷原子[8]、自旋[9]、光波导[10]以及声波波导[11]等实验系统中观测到了量子化的拓扑泵浦现象.最近,在拓扑系统中,探索相互作用引起的新奇的泵浦现象日益受到人们的关注.例如由相互作用诱导的非线性拓扑泵浦,其特征为中等强度的非线性支持孤子态的量子化输运,而强非线性使得孤子态呈现局域特性.通过理论研究,人们提出可以利用液晶[12]、超冷原子[13,14]和光波导[15]系统具有的非线性效应,实现对非线性拓扑泵浦的探索.到目前为止,人们仅在光波导系统中通过引入克尔型吸引非线性观测到了量子化的整数[15]和分数拓扑泵浦现象[16].所以,在不同的系统中开展进一步的研究工作仍然是有必要的,可以更深入地理解非线性拓扑泵浦现象并探索其应用前景.

在超冷原子系统中,人们可以利用光晶格[17]和Feshbach 共振[18]技术对原子之间的相互作用进行精确的调控,这使其成为研究由相互作用诱导的非线性效应的理想平台.例如人们已经研究了物质波孤子[19]和非线性局域化[20]等现象.特别是,随着超冷原子动量晶格技术的发展[21],可以利用其具有的晶格参数和系统相互作用可独立精确调制的特性,来研究非线性动力学和拓扑物理,并在实验上观测到了相互作用导致的自陷俘效应[22]以及对迁移率边的影响[23].值得注意的是,在超冷原子系统关于拓扑泵浦的研究中,相对于线性拓扑泵浦而言,对于非线性拓扑泵浦的研究仍然很少.因此,本文提出可以利用超冷原子动量晶格系统来演示非线性拓扑泵浦,为进一步探索非线性拓扑输运提供了一定的指导.

本文用数值求解方法计算一维非对角Aubry-André-Harper (AAH)模型的非线性能带结构随相互作用强度的变化,并分析了孤子态的非线性拓扑泵浦具有量子化的输运特征.进一步,基于7Li 原子的动量晶格系统,提出了一个演示非线性拓扑泵浦的方案,并分析了绝热演化条件对泵浦过程的影响.结果表明,在动量晶格系统中演示非线性拓扑泵浦具有可行性.本文为在超冷原子系统中研究非线性拓扑泵浦提供了一个可行的途径,可进一步扩展对非线性拓扑现象的研究.

全文结构安排如下: 第2 节对一维非对角AAH模型的非线性能带和孤子态进行分析;第3 节对不同相互作用系统中非线性泵浦过程进行了分析;第4 节基于7Li 原子的动量晶格系统,提出了一个具体的非线性拓扑泵浦方案.第5 节是对非线性拓扑泵浦的总结与展望.

2 理论模型

本方案研究的是一维非对角AAH 模型[24−26]的非线性拓扑泵浦.如图1(a)所示,在一维非对角AAH 模型中,每个原胞包含3 个格点(分别表示为A,B和C),最近邻格点之间的耦合强度分别为Jab(t) ,Jbc(t) 和Jca(t),且每个格点上的能量均为零.在紧束缚近似下,一维非对角AAH模型的有效哈密顿量表示为

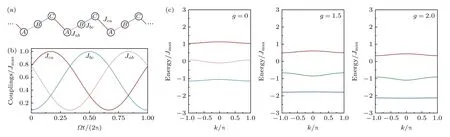
图1 (a)一维非对角AAH 模型示意图,每个晶格原胞有3 个格点(A,B,C),最近邻格点之间的耦合强度(Jab,Jbc,Jca)随时间变化,每个格点上的能量设置为零;(b)在一个泵浦周期内,耦合强度的周期性调制函数 (由(2)式定义);(c)在 Ω t=0 时刻,非对 角AAH 模型非线性能带结构在不同相互作用强度 g=0,1.5,2.0 下的分布.图中的物理量均以 Jmax 为单位,耦合强度值Jab=0.77,Jbc=0.10 和Jca=0.77Fig.1.(a) Schematic illustration of 1D off-diagonal AAH model with three sites (A,B,C) per unit cell and time-dependent couplings (Jab,Jbc,Jca) between neighbouring sites;(b) variation of the couplings during one pumping cycle defined by Eq.(2);(c) energy bands of nonlinear off-diagonal AAH model vs.interaction strength g.All quantities shown in the pictures are given in units of Jmax,with coupling strength values Jab=0.77,Jbc=0.10 and Jca=0.77 .

其中,j=0,1,2 分别对应的是Jab(t),Jbc(t) 和Jca(t)耦合项;Jmax表示系统的最大耦合跃迁强度,设定Jmax=1 作为能量单位;Ω为耦合强度的调制频率,要求调制频率尽可能低,以满足绝热演化条件.在一个调制周期内(Ωt=2π),耦合强度的调制曲线如图1(b)所示.同时,根据不同的J/K比值,一维非对角AAH 模型具有不同的拓扑特征[27].本文选择J=0.55 和K=0.45,那么系统3 个能带的陈数分别为C={-1,2,-1}.

进一步,在一维非对角AAH 模型的基础上,考虑到平均场相互作用带来的格点上的非线性项,那么,第n个原胞中A,B和C格点的波函数演化将由一组离散的非线性薛定谔方程决定,具体如下:

其中,φn,a(t),φn,b(t),φn,c(t) 分别表示在t时刻原胞n中3 个格点上的波函数振幅;g＞0 (或g＜0)表示相互作用强度.

之后,通过求解定态薛定谔方程H(k,Φ(k))Φ(k)=EΦ(k),就可以得到非线性系统的本征值(E)和本征态(Φ(k)).具体而言,采用的求解过程如下所示.将定态薛定谔方程H(k,Φ(k))Φ(k)=EΦ(k) 展开后,可以得到:

该方程组是一个6 元目标函数F(X)=(F0,F1,F2,F3,F4,F5)T,其中X=(E,a,b,c,u,v) 为变量.对每个方程均求一阶偏导数后,可以得到目标函数F(X) 的雅可比矩阵J(X) .之后,通过牛顿迭代法,利用泰勒展开式对目标函数进行局部近似,并通过求解近似函数的根来逐步逼近方程的真实解,得到E,a,b,c,u,v这6 个变量的解,从而得到能量E和波函数Φ(k)=(ϕa,ϕb,ϕc)T.

利用上述数值计算方法,计算了在相互作用强度g＞0 的情况下,非对角AAH 模型的非线性能带结构,结果如图1(c)所示.这里设定的是Ωt=0时刻的耦合强度值,即Jab=0.77,Jbc=0.10 和Jca=0.77.从图中可以看出,能带结构因相互作用的存在产生了改变.随着g强度的增加,第二能带和最高能带的能量发生了偏移,但其能带的色散关系没有发生变化.相比之下,最低能带除了发生了能量偏移,其能带色散关系也出现了调制,从具有色散特征的能带逐渐变成了平带结构.对于一个无色散的平带系统而言,系统的群速度为零,波包可以作为一个整体在晶格中进行演化,表现为物质波孤子态[28].

图2(a)是在相互作用g＞0 情况下,最低能带的孤子态分布.该孤子态主要分布在单个原胞3 个格点上,且φn,a,φn,c和φn,b之间存在着π 相位.如图2(b)所示,将这种孤子态作为初始注入态,在g ＞0的非线性系统中进行淬火动力学演化,可以发现孤子态表现出局域化效应.采用同样的方法,也可以计算出相互作用g＜0 非线性的非对角AAH 模型的能带结构随g的变化,如图2(d)所示.可以看出,g＜0 的相互作用主要是对最高能带的结构产生调制,使其从具有色散特征的能带逐渐变为平带结构.如图2(c)所示,其本征态同样具有孤子态的分布特征,且3 个格点上的波函数是同相位的.这些结果为进一步探索非线性系统中的拓扑泵浦现象提供了基础.

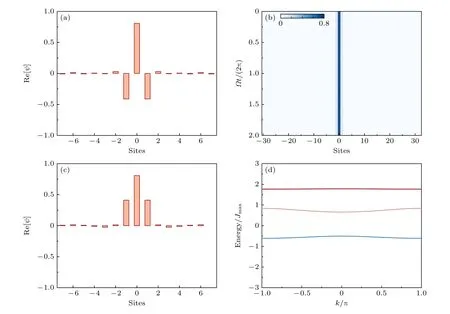
图2 (a),(b)在 g ＞0 的 系统中,计算得到的最低能带的孤子态的波函数分布,在淬火动力学演化过程中是严格局域化的;(c),(d)在 g ＜0 的系统中,最高能带的孤子态波函数分布和能带结构的分布Fig.2.(a),(b) In the system of g ＞0,the wave function distribution of soliton state for the lowest energy band is strictly localized in the process of the quench dynamics;(c),(d) in the system of g ＜0,the wave function distribution of soliton state for the highest band and the energy band structure.

3 结果分析

接下来,对非线性系统中的孤子态的拓扑泵浦过程进行了分析.分别在g＞0 和g＜0 区间选取了一个典型的相互作用强度值,对孤子态的演化过程进行了数值求解.图3(a)给出的是在无相互作用系统中的线性拓扑泵浦过程.这里选择的初始态为占据最低能带(C0=-1)的瓦尼尔态,且耦合强度的调制频率为Ω/Jmax=0.02,满足绝热演化条件.在这种情况下,物质波包的衍射效应呈主要作用,波包在演化过程中存在着明显的色散.在一个泵浦周期内,波包质心向左移动了3 个晶格格点的距离,具有量子化泵浦的特征,受所占据能带的陈数决定.随着相互作用的增强,系统会产生稳定的非线性拓扑孤子态,波包作为整体在晶格中进行移动,此时相互作用起到了将波包局域化的效果.图3(b)给出的是g=1.5 情况下的非线性拓扑泵浦.选择的初始态和图2(a)所示的波函数分布形式一致,是处在最低能带上的孤子态分布,耦合强度的调制频率为Ω/Jmax=0.01,满足绝热演化条件.在每个泵浦周期内,质心仍遵循向左移动3 个晶格格点的距离,仍由最低能带的陈数决定.利用同样的方法,计算了在g=-1.5 的系统中,对于占据最高能带的孤子态(图2(c)),同样表现为具有量子化的非线性拓扑泵浦过程,结果如图3(c)所示.

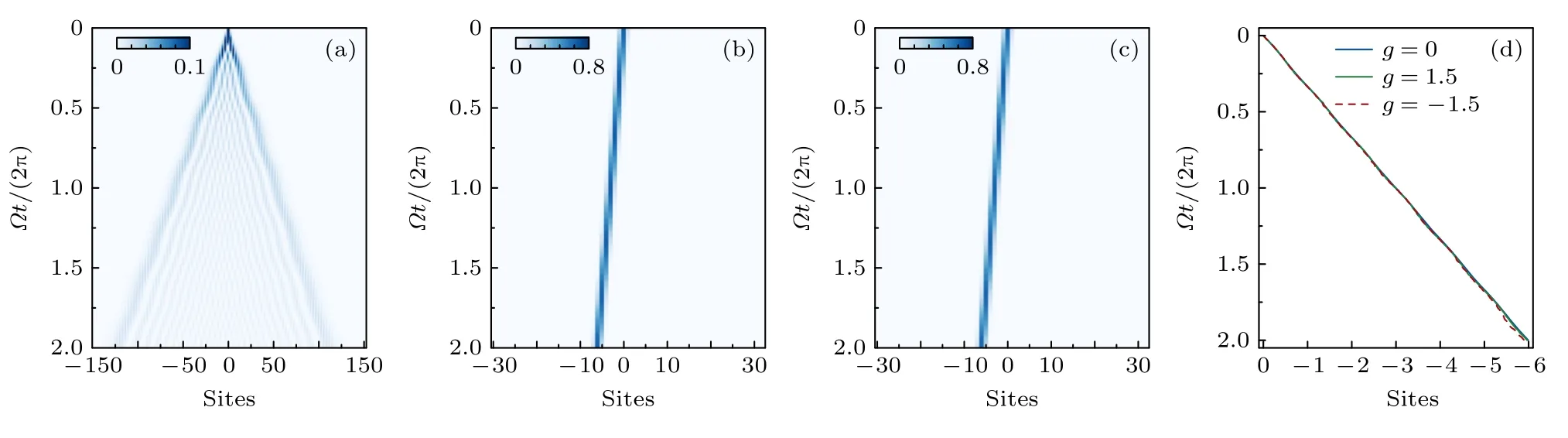
图3 非线性拓扑泵浦 (a) g=0 系统中,最低能带上分布的瓦尼尔态的线性泵浦演化;(b) g=1.5 系统中,最低能带的孤子态的非线性演化;(c) g=-1.5 系统中,最高能带的孤子态的非线性演化;(d) 在两个泵浦周期内,系统的质心位移结果.上述结果均是对(3)式进行数值求解所得,所用参数: (a)耦合强度 Jmax=1,调制频率 Ω/Jmax=0.02,原胞数 Nc=101 ;(b),(c)耦合强度Jmax=1,调制频率 Ω/Jmax=0.01,原胞数Nc=21Fig.3.Interaction induced nonlinear propagation in topological pumps: (a) At g=0,the linear pump evolution of uniformly distributed Wanier states at the lowest band;(b) at g=1.5,the nonlinear evolution of the soliton state for the lowest occupancy band;(c) at the g=-1.5,the nonlinear evolution of the soliton state for the highest occupancy band;(d) displacement of the centre of mass for the cases shown in a to c.The results are obtained by numerically solving Eq.(3) with parameters: (a) Jmax=1,Ω/Jmax=0.02,Nc=101 ;(b),(c) Jmax=1,Ω/Jmax=0.01,Nc=21 .

通过对非线性拓扑泵浦过程的数值分析可以得到,在较弱的相互作用强度条件下,系统存在的孤子态的演化过程满足量子化的输运特征.同时,利用本文提到的数值求解方法对系统的能带结构进行求解H(k)|Φn(k)〉=En(k)|Φn(k)〉,得到了能带和波函数.那么第n个能带对应的陈数为[29]

其中,Fn=〈∂tΦn|∂kΦn〉-〈∂kΦn|∂tΦn〉 为贝里曲率.这里,采用数值方法[30]对能带陈数进行计算,具体结果如图4 所示,在g＞0 的弱相互作用区间,最低能带的陈数保持为C0=-1 ;在g＜0 的弱相互作用区间,最高能带的陈数保持为C2=-1 .同样,Jürgensen 等[15]通过一种自定义的间接方法,在弱相互作用区间对最低能带的陈数进行了计算,陈数也为C0=-1 .

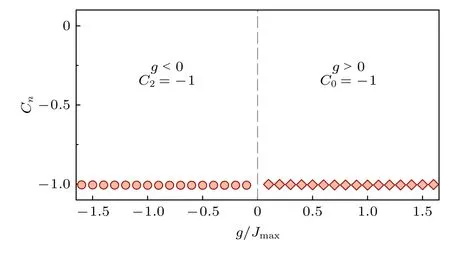
图4 在 g ＞0 和 g ＜0 的弱相互作用系统中,分别计算最低能带的陈数 C0 和最高能带的陈数C2Fig.4.Chern number associated with the energy band are calculated for g ＞0 and g ＜0 in the regime of weak interaction strengths,respectively.

4 实验方案

本节基于玻色子7Li 原子的动量晶格系统,提出了一个演示非线性拓扑泵浦的实验方案.图5(a)简要描述了动量晶格的实现原理[21].将一对对射晶格光(波长为λ)照射到BEC 原子团上,其中向右传播的晶格光包含单一频率(E+cos(kx-ω++ϕ+)),而向左传播的晶格光中包含多个频率成分.通过双光子布拉格跃迁,每对光场 (ω+和) 都会对相邻的动量态(|n〉 和|n+1〉)之间的耦合跃迁产生影响.这里,晶格光的波长为λ=1064 nm,远 失谐 于7Li 原子 的能级跃迁线(671 nm).同时,对于处在基态原子团的色散关系可以近似处理为自由粒子的色散关系,那么相邻动量态|n〉 和|n+1〉 之间的能级差为ΔE=4Er(2n+1),其中,原子的反冲能 量Er=ℏ2k2/(2M) (M是原子质量),对于λ=1064 nm 的晶格光,Er=2π× 25 kHz.并且,每对光场 (ω+和) 之间的频率差满足 4Er(2l+1)/ℏ,相位差满足.那么,描述动量晶格系统的哈密顿量可以表示为

图5 利用动量晶格系统演示非线性拓扑泵浦方案 (a) 动量晶格示意图;(b) 初态制备过程;(c) 在两个泵浦周期内,调制频率为 Ω/Jmax=0.5 时孤子态的动力学演化;(d) 在两个泵浦周期内质心移动的晶格距离(红线为动量晶格的实际哈密顿量计算的结果,蓝线为理想哈密顿量计算的结果);(e) 绝热演化条件分析,不同 Ω/Jmax 对应的每个泵浦周期质心位置的移动距离.设置参数为: Jmax=2π×10.0 kHz,U/Jmax=1.5,Nc=21Fig.5.Implementatial proposal of nonlinear topological pumping based on the momentum lattice: (a) Schematic diagram of the momentum lattice;(b) preparation of initial state;(c) dynamics evolution of soliton state in two pumping periods,with modulation frequency of Ω/Jmax=0.5 ;(d) lattice displacement of the center-of-mass during two pumping periods (The red line is the result calculated from actual Hamiltonian of the momentum lattice,and the blue line is the result of the ideal Hamiltonian);(e) analysis of adiabatic evolution conditions.The shift of center-of-mass for each pumping period corresponding to different values of Ω/Jmax .Parameters are: Jmax=2π×10.0 kHz,U/Jmax=1.5,Nc=21 .

在平均场近似和Hartree-Fock 近似处理下,每个动量态波函数的动力学演化均由Gross-Pitaevskii (GP) 方程决定,其表达式与(3)式类似,即

其中,相互作用强度项为U=4πℏ2asρN/M(ρN是BEC 原子团密度,as是s 波散射长度).通过Feshbach 共振[18]技术调节原子间的散射长度as,可实现对相互作用的精确调节.同时,在不同演化时刻下,系统波函数的分布均需满足归一化条件,即

在动量晶格系统中演示非线性拓扑泵浦方案,表征原子团输运特征的观测量可以定义为在一个泵浦周期内原子团的平均动量的变化量,即

其中,n为动量态 |n〉 对应的晶格格点坐标;|φn(t)|2表示原子分布在动量态 |n〉 的概率;动量态质心移动的距离单位是 2 ℏk.实验中可以通过时间飞行测量来探测所有动量态的原子团的密度分布,从而得到不同演化时刻下的所有动量态分布情况,即|φn(t)|2.通过(10)式可计算出原子团的平均动量移动的距离.

下面对演示方案进行具体描述.由文献[31,32]可得,对于|F=1,mF=1〉 内态的7Li 原子系统,可以利用Feshbach 共振技术精确调控原子间的相互作用.当囚禁BEC 原子团的势阱频率为(ωx,ωy,ωz)=2π×(70,800,800) Hz,并在偏置磁场强度调节到710 G 左右,即散射长度达到约 200a0(a0表示玻尔半径)时,可以得到原子数为N=3.0×105的BEC 原子团.在动量晶格中,设定最大耦合强度为Jmax=2π×10 kHz,且满足Jmax≪8Er的条件.同时设定偏置磁场为B=731.548 G左右,使得s 波散射长度为as≈1000a0,可调控相互作用强度为U/Jmax=1.5 .

为了在动量晶格系统上更方便地制备初态并演示非线性拓扑泵浦过程,将初态构造成近似满足孤子态的形式,即将波函数全部分布在中间原胞的格点上,而其他原胞格点上的分布忽略不计.图5(b)是初态制备的示意图.这里选择将|-1〉,|0〉,|+1〉3 个动量态组成初态所占据的原胞.在t=0 时刻,系统处在零动量的BEC 状态,此时波函数为Ψ0=(0,1,0)T.之后,同时打开|-1〉,|0〉 和|0〉,|+1〉动量态之间的耦合跃迁项,分别设置为Je-iθ和Jeiθ,原子会在3 个动量态格点之间进行拉比振荡.经过时间t的演化,得到的目标初始态为Ψini=这样,通过选择合适的耦合项参数J,θ和时间t,就可以制备所需要的初始态.如当选择参数J=2π×4.0 kHz,θ=π/2 和t=18.1µs 时,初 始态分布为Ψini=(-0.424,0 .800,-0.424)T,满足相互作用为U/Jmax=1.5 的系统对孤子态分布的要求.

图5(c)给出了在相互作用强度为U/Jmax=1.5的系统中,上文所示初始态的非线性泵浦过程.这里,相邻动量态之间的耦合强度按照(2)式进行调制,设定的最大耦合强度为Jmax=2π×10.0 kHz,调制频率为Ω/Jmax=0.5,系统原胞数为Nc=21 .从图5(d)所示的质心位移结果可以发现,计算得到的质心位移值基本上体现出了量子化的输运特征,但其与理想值 〈pc〉=-3.0 之间仍有一定偏离,主要是受到实际动量晶格中的非共振的多频率光带来的能级失谐和系统绝热演化条件等因素的影响.

通过数值分析,评估了演化过程中的绝热条件对非线性泵浦效果的影响,如图5(e)所示.计算了在不同的调制频率Ω/Jmax情况下,单个泵浦周期内原子动量态质心 (〈pc〉) 移动的晶格距离.从图中可以看出,调制速率越慢,即Ω/Jmax越小,〈pc〉越接近理想的移动距离 〈pc〉=-3.0 .随着Ω/Jmax的增加,逐渐破坏演化过程所需要的绝热条件,〈pc〉 会逐渐偏离理想值.当Ω/Jmax=0.5 的时候,〈pc〉≈2.8,基本也能够体现出非线性拓扑泵浦的主要特征.并且,在此调制频率下,每个调制周期所需的时间为T=2π/Ω=0.2 ms,这样的参数在实验上具有一定的可行性.同时,考虑到囚禁BEC 原子团的外势阱形状对原子团分布和相干演化时间的影响,动量晶格系统演化的相干时间在1 ms 以内.这样,基本上可以从3 个调制周期内的动力学演化结果中得到能带的陈数.

5 结论

本文使用数值求解方法计算了一维非对角AAH 模型的非线性能带和孤子态解,并分析了在g ＞0 和g＜0 的相互作用系统中,存在着处于最低能带和最高能带的孤子态的量子化的输运现象.此外,基于7Li 原子的动量晶格系统,还提出了一个演示非线性拓扑泵浦的实验方案,并分析了其在动量晶格实验上的可行性.本文为在超冷原子系统中实现非线性拓扑泵浦提供了一个新颖且可行的途径,可进一步用于研究非线性系统的拓扑输运现象,例如边界态在相互作用系统中的拓扑输运[33−35].

感谢中国科学技术大学郑炜教授和罗祎帆博士的有益讨论.