弹线膛一体径向精锻成形身管内膛轴向褶皱缺陷的形成机理
2023-09-06杨宇召樊黎霞
杨宇召 杨 晨 徐 诚 樊黎霞
南京理工大学机械工程学院,南京,210094
0 引言
径向精锻工艺成形效率高、精度好,是世界各国加工身管的主流工艺。身管的内膛由弹膛和线膛两部分组成,我国将弹膛和线膛一体成形的径向精锻工艺称为弹线膛一体径向精锻工艺,其芯棒含有弹膛和线膛的特征,然而该工艺成形的身管出现过炸膛事故,炸膛原因至今不明确,因此一直未在实际生产中应用,导致我国的身管制造只能将弹膛和线膛分开加工,先用纯线膛径向精锻工艺成形线膛,然后再用铰削工艺单独成形弹膛,两次工艺需要重新定位,导致效率低且身管同轴度不高,影响身管的射击精度。欧美国家早已实现弹线膛一体径向精锻成形,而我国只能采用纯线膛径向精锻的妥协之举,弹线膛一体径向精锻工艺已成为我国身管制造的瓶颈。
国外关于锻造身管炸膛的公开研究很少,国内王涛[1]最早探讨弹线膛一体径向精锻工艺成形身管的炸膛现象,分析了锻后身管去应力前后的力学性能变化,将炸膛现象归因于锻后身管的残余应力。然而,XU等[2-3]系统地研究了不同身管材料锻后的残余应力分布,经过600 ℃热时效后,残余应力能被消除80%以上。樊红伟等[4]研究了残余应力对锻后身管的力学性能影响,发现去应力后身管性能得到了恢复。弹线膛一体径向精锻身管都有去应力退火阶段,因此无法认定残余应力是导致炸膛的原因。田文松等[5]分析认为炸膛是由于氢脆,这个分析集中在个案上,材料无氢脆弹线膛一体径向精锻后也出现过炸膛。近年来,YANG等[6]研究发现,弹线膛一体径向精锻身管在下沉段内壁会形成轴向的褶皱,而褶皱缺陷在进入锻造段后,在持续的挤压下会形成裂缝,裂缝将严重影响身管的安全,因此下沉段形成的褶皱可能是导致弹线膛一体径向精锻成形身管炸膛的原因之一。
国内外对径向精锻工艺造成内膛褶皱的相关研究并不多,GHAEI等[7]利用二维精锻有限元模型模拟无芯棒锻打过程发现,在没有芯棒的情况下,管内表面的轴向拉应力可能导致锻造后的身管产生周向的褶皱与裂纹,但该研究没有实验验证,且研究得出的裂纹方向是沿周向的。LI等[8-9]利用三维有限元径向锻造模型研究薄壁铜管的成形时发现,管材内壁在锻打过程中产生了轴向褶皱,且利用电镜观察铜管内部验证了有限元模拟,进一步的有限元模拟发现,内壁的褶皱会演变成轴向的裂纹,而裂纹有可能导致管材在承压时出现破裂的现象。陈修琳等[10]研究发现,铍青铜QBe2薄壁管在径向冷锻过程中会出现纵向裂纹。关于锻造身管的缺陷,刘金明等[11]研究发现,在弹线膛一体径向精锻成形身管的弹膛锥角处会形成圈纹缺陷,然而圈纹缺陷与本文的轴向褶皱缺陷方向不同。童维等[12]利用有限元仿真以及形貌测量研究了弹线膛一体径向精锻成形身管下沉段褶皱的形貌演化情况。周勐弢等[13]根据材料性能研究了精锻身管下沉段开裂的判据。然而上述研究均没有涉及弹线膛一体径向精锻成形身管的褶皱缺陷的形成机理。
尽管关于径向精锻工艺成形缺陷的研究较少,但是旋锻工艺以及皮尔格轧管工艺(pilgering)都与径向精锻工艺类似,故可将这两种工艺的缺陷研究作为参考。在旋锻成形管件中,常见的缺陷有褶皱、裂纹、飞边以及扭曲等[14]。石松等[15]和孙子莹等[16]研究了无芯棒径向进给参数对旋锻成形车轴的影响,发现车轴内圆会出现几何凹陷。王宏等[17]采用有限元分析了旋锻过程中工件是否出现损伤缺陷等。王俊士等[18]研究了不同锤头入口曲面对旋锻成形管件变形的影响,发现管件端部会出现凹坑现象。皮尔格轧管工艺中工件变形也是先减径后减壁厚,与弹线膛一体径向精锻工艺类似,ABE等[19]研究了皮尔格成形管件内壁的轴向褶皱缺陷,并形成了工件可加工性的判据。李恒等[20]系统总结了皮尔格轧管工艺的研究进展,认为管件在减径减壁厚过程中的宏观不均匀变形是该工艺的研究难点,而宏观变形的不均匀会带来缺陷以及精度的问题。
旋锻和皮尔格轧管工艺一般用于生产薄壁管件,而身管属于厚壁管,尽管上述学者的部分研究涉及了工艺产生的褶皱缺陷,但是大部分都集中在工艺参数对成形的影响上,较少研究缺陷的形成机理。
综上所述,国内外公开的关于径向精锻工艺成形的厚壁管件内壁褶皱缺陷,特别是针对弹线膛一体径向精锻工艺成形身管的研究均处于空白,为了探究弹线膛一体径向精锻成形身管内膛轴向褶皱缺陷的形成机理,本文采用有限元方法,建立三维径向精锻有限元模型,模型中考虑了大部分径向精锻的工艺参数,如毛坯尺寸、旋转进给、轴向进给、锤头参数以及夹持压力等。利用仿真研究褶皱的形成机理以及工艺参数对褶皱成形的影响,同时还设计了径向精锻实验成形身管,对有限元结果进行验证。
1 三维径向精锻有限元的建立
径向精锻工艺的锻造锤头分布如图1所示,四个锤头沿工件周向均匀分布,对身管毛坯进行高频径向锻打,完成减径与减壁厚过程,而身管的膛线则是依靠表面带有膛线特征的芯棒来成形。弹线膛一体径向精锻工艺如图2a所示,纯线膛径向精锻工艺如图2b所示,弹线膛一体成形和纯线膛成形两种工艺都是径向精锻工艺,区别在于芯棒以及毛坯的内径。与纯线膛精锻相比,弹线膛一体成形工艺中工件需要先完成减径即经历下沉段过程,然后才能与芯棒接触,进入锻造段。由于褶皱是沿轴向的,故常用的二维轴对称径向精锻有限元模型已经不再适用,身管径向锻造时,工件除了轴向的进给外,还需要旋转,另外实际的锤头也并不是圆弧形状,径向锻造过程不是完全轴对称的,因此本文需要建立弹线膛一体径向精锻工艺的三维有限元模型。

图1 径向精锻工艺锤头分布图

(a)弹线膛一体径向精锻

(b)纯线膛径向精锻图2 径向精锻工艺示意图
1.1 材料模型
工件的材料为30SiMn2MoVA钢,该材料是我国常用的身管制造材料,材料属性来自FAN等[21]的研究,在有限元模型中,材料模型为弹塑性,本构关系为σ=Kεn(σ为应力,ε为应变,K、n为幂强化材料本构模型的常数)。各项参数如表1所示。

表1 工件的材料参数
1.2 几何模型及边界条件
三维径向精锻的有限元几何模型如图3所示,模型包含沿周向均匀分布的四个锤头和身管部件,限制身管轴向进给速度的挡块简化为与身管端面耦合的参考点。由于褶皱是在下沉段减径过程中产生的[6],而下沉段毛坯与芯棒是无接触的,且进入锻造段与芯棒接触后褶皱会被打平或形成裂缝,不容易直观地看到,故本文数据点的提取位置以及研究重点均在下沉段,而芯棒对下沉段是无影响的,因此在模型中将芯棒部件移除。

图3 身管径向精锻三维有限元模型
对于工件在旋转过程中的复位问题,本文定义相应的弹性单元来代替弹性杆。身管部件单元类型为带有沙漏控制的缩减积分单元C3D8R。身管网格使用ALE网格,其自适应功能可使身管网格在变形过程中保持良好的质量。
锤头为刚体,单元类型为节点刚性单元R3D4,其几何形状与工厂目前使用的一致,如图3所示。图4中标出了径向精锻的工艺参数含义,模型中设置的相关工艺参数值如表2所示,模型中接触面采用库仑摩擦模型,摩擦采用罚函数法,滑移公式为有限滑移公式,锤头与工件的摩擦因数为0.15[21]。身管的径向精锻在常温下进行,且加工过程中有持续的冷却液,因此模型里的温度设置为常温,忽略温度的影响。

图4 加工参数示意图
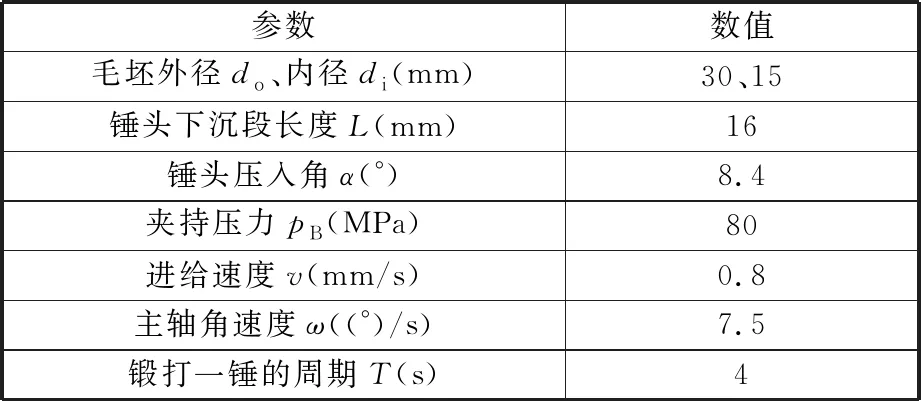
表2 径向精锻工艺参数(对照组)
模型还考虑了工艺参数对褶皱的影响,因此根据控制变量方法的原则,每个模拟算例仅更改一个工艺参数,具体参数如表3所示,对照组的工艺参数如表2所示。

表3 几何和工艺参数(控制变量组)
2 径向精锻实验
采用GFM SKK-10冷径向精锻机进行径向精锻实验,实验用材料为30SiMn2MoVA钢,在实验中用L表示每个实验试件,加工工艺参数如表4所示,其中d1和d2是锻后工件的外径和内径尺寸,Q是锻造比。将锻后身管的下沉段切割制成图5所示的试件,用电镜(型号FEI Quanta 250F)观察图中1、2位置处的形貌,位置1是下沉段开始处,也表示毛坯的形貌,位置2是下沉段结束处的位置。
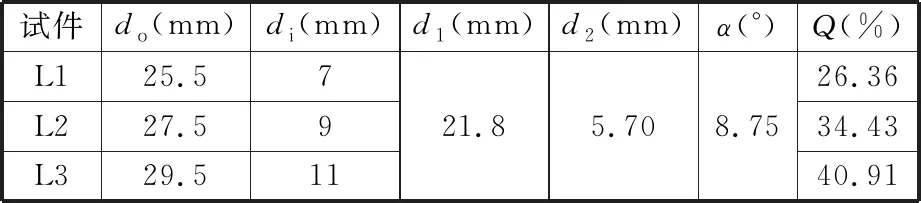
表4 径向精锻实验工艺参数

图5 锻后身管试件
3 有限元模型验证
径向精锻有限元的正确性大部分通过对比仿真得到的锻造载荷与实验结果来验证。本文为在仿真中直观地观察褶皱,在保证毛坯管仍然是厚壁管的情况下将仿真中的毛坯内径扩大设置为15 mm,而实际工厂中没有该型号的毛坯管,无法直接通过实验验证本文有限元模型的正确性,因此,将本文建立的三维有限元模型的毛坯尺寸修改为文献[21]的径向锻造实验中的尺寸,并将模拟结果与实验值[21]进行对比以验证有限元模型。表5所示为文献[21]中的径向锻造实验工件尺寸,在本文建立的三维有限元模型中添加芯棒部件,按表5的尺寸数值修改本文的有限元模型,模拟得到的锻打力如表5所示,将模拟锻造载荷与实验结果进行比较,模拟结果大于实验结果,这与文献[21]的研究结果一致。仿真与实验误差在10%以内,表明所建立的三维径向精锻有限元模型可以用来定性分析径向精锻身管下沉段内壁褶皱的形成机理以及工艺参数的影响规律。

表5 验证实验的工艺参数
4 结果分析
4.1 褶皱的形成机理
由于锤头之间存在间隙,所以锤头压下去时身管的径向变形并不是均匀的,锻打第1锤身管变形如图6所示,可以看出,当锻打第1锤压下后,身管在锤头间隙处的变形与其他位置不同,间隙处的变形比其他区域要大,相应地,由于变形的不同,其径向位移u1也不同,沿轴向的褶皱实际上就是由内壁圆周上点的径向位移不一致造成的,可以明显观察到内膛的圆孔开始变得不规则了。

(a)等效塑性应变

(b)柱坐标下的径向位移u1图6 锻打第1锤身管变形
随着锻打的继续,身管向前进给并且旋转一个角度,锻打第2锤身管变形如图7所示,身管的径向不规则变形加剧,内壁圆周对应锤头间隙的位置有较大的应变,同时在第1锤时有较大应变的点转到了其他位置,由图7可以看出,身管内壁大应变的点约为8个,各点的径向位移也不均匀,圆形已经变得很不规则了。

(a)等效塑性应变

(b)柱坐标下的径向位移图7 锻打第2锤身管变形
身管工件在锻打过程继续旋转进给,在多次锻打后,工件变形情况如图8所示。锤头的工作面为平面,在多次锻打后,身管外部为近似圆形的正多边形,多次锻打后其内膛的圆形非常不规则,横截面形状已变为近似正方形,这说明在工件外部受力不均的情况下,内孔的变形将会变得不规则。由图8b可以看出,内膛产生了许多沿轴向的褶皱,径向变形越大,褶皱越明显。

(a)外部变形(等效塑性应变)

(b)内部变形(等效塑性应变)图8 多次锻打后身管变形 Fig.8 The deformation of the workpiece after the multiple forging beats
根据有限元分析,将弹线膛一体同锻身管内膛产生沿轴向褶皱的机理总结如下:图9所示为某一横截面在下沉段的锻打过程,在锻打第1锤时,由于锤头存在间隙,锤头压下时,处在间隙区的身管材料的变形与受到锤头锻压的区域的变形不一致,从而导致身管内膛圆周各点的径向位移不同,这就使得内孔的圆形发生了变化;身管旋转进给,在下一锤时新的位置转到了锤头的间隙区,身管径向位移的不一致又被加剧,内孔圆形逐渐变为不规则的形状,从而形成了褶皱。弹线膛一体同锻身管内膛产生褶皱的机理与文献[8]中圆弧截面锤头径向精锻成形的薄壁铜管产生褶皱的机理一致,都是由于锤头间隙区的存在。

图9 下沉段褶皱形成机理示意图
4.2 褶皱的成形判据及验证
由上述分析可知,弹线膛一体同锻身管内膛的褶皱是由锤头间隙引起的,在分析内孔的变形过程中发现,在初始锻打时,虽然内孔不再是圆形,但是也仅仅是变得不规则,并没有形成褶皱,比如说在当前这一锤锻打后某点处有了形成褶皱的趋势,但是在下一锤时,身管旋转了一个角度,锤头锻打下来后,原来有形成褶皱趋势的位置在新一锤下这种褶皱趋势又没有了。为了详细研究褶皱的成形过程,取身管下沉段内膛的一横截面,对该截面的内壁单元节点顺次编号,如图10所示,输出每节点在下沉段每一锤结束后的径向位移,相邻点的径向位移之差就是褶皱,每一锤锤头的径向进给量是相等的,每打一锤工件旋转一个角度,每一锤次锻打时四个锤头是同时压下的。
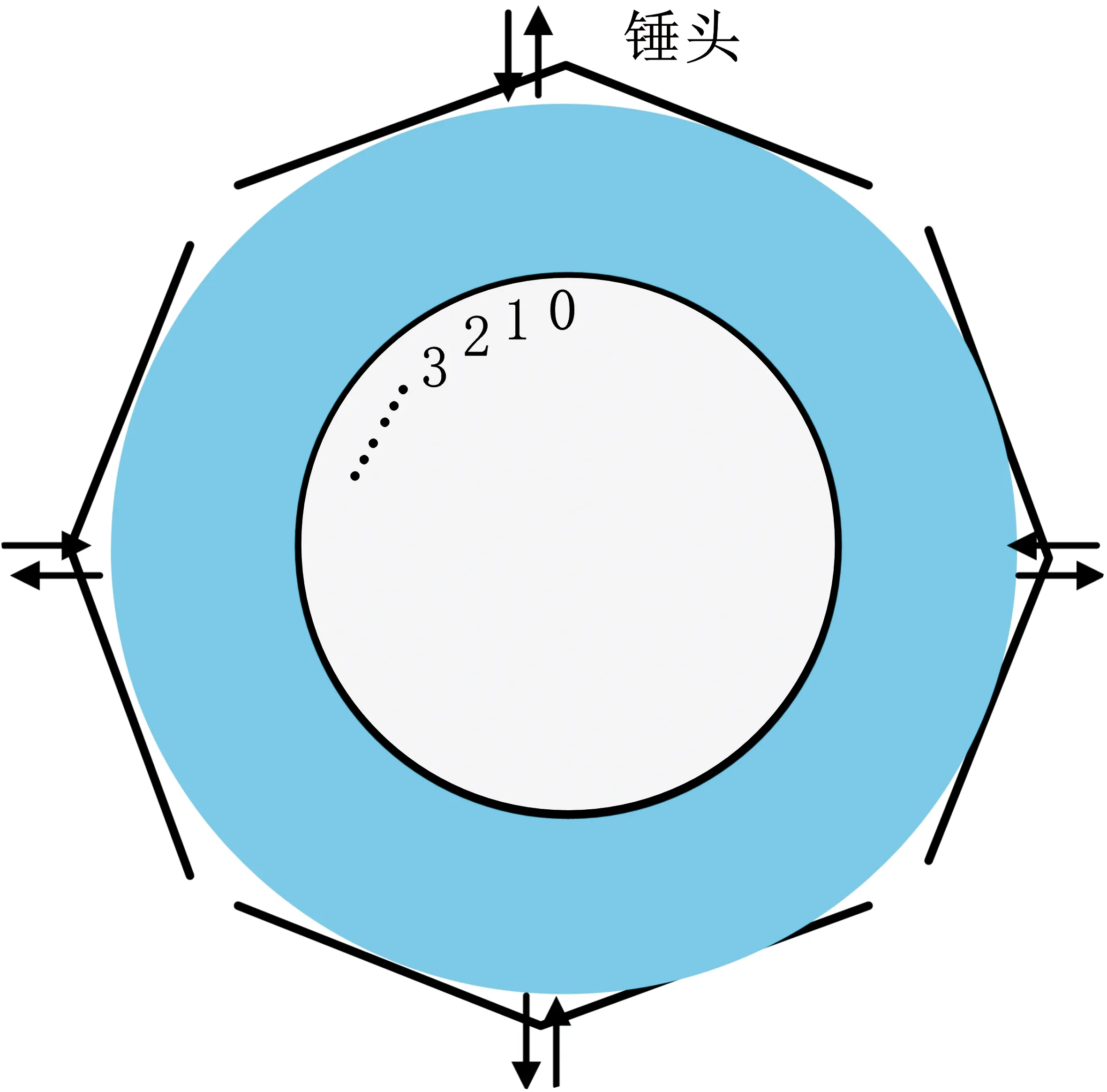
图10 身管内膛截面节点编号
内表面节点的径向位移如图11所示,第1锤次打下后,内表面出现了四个波谷,对应节点12、35、57及79,波谷位置对应的是锤头间隙处,即处于锤头间隙处的节点的径向位移要比其他节点的径向位移小,实际上,波谷就相当于褶皱,只是由于褶皱的宽度太大,高度较小,因此不明显。打第2锤时,由于工件的旋转,新的节点对应于锤头的间隙处,该处节点的位移较小,此时内表面位移的波谷位置为节点21、43、65及87。第3锤打下后,波谷继续转移到其他节点。从第4锤开始,波谷仍然转移到其他节点,曲线上不仅有四个较大的波谷,也可以观察到曲线不光滑了,出现了很多细碎的小波峰波谷。同样地,继续将后续锻打次数的内表面节点位移输出,如图12所示,可以看出,不同锤次之间的径向位移相差较大,直接输出径向位移不利于比较每一锤的波峰波谷的大小变化(实际上就是褶皱大小的变化),因此需要将径向位移做一定的数据处理以方便比较。提取每一锤的径向位移曲线上数值最小的点,将该曲线上其他点的径向位移都减去该点的位移,也就是说统一地将波谷平移到径向位移为0的水平线上,这样可以直观地观察每一锤打下后,波峰波谷的高度变化。
由图12可以看出,从第4锤后,曲线仍然有四个主要的波峰波谷伴随着多个细碎的波峰,与前三锤的径向位移曲线相比变得非常尖锐,并且波峰波谷固定在某些节点上。随着锻打的继续,工件持续转动,这些特征不再随着工件的转动而转移至其他节点,唯一变化的是波峰的高度,本文将波峰波谷不再移动的起始状态定义为褶皱形成,也就是说从第4锤结束后,褶皱就形成了,后续每一锤次的作用是增加褶皱即波峰的高度。
按照上述方法统计所有算例的结果,均发现其褶皱的形成符合上述褶皱成形的判断,并不是本文呈现出来的这一个有限元计算模型的偶然结果。根据表3所示的控制变量组,更改工艺参数,如主轴角速度、锤头角度、进给速度、身管毛坯尺寸、夹持压力等,分别进行有限元仿真,提取下沉段内表面节点的位移,结果都会在若干锤数后出现波峰波谷位置固定的现象,总结这些现象提出上述关于褶皱形成的判断。
虽然可以通过内膛节点径向位移曲线的波峰波谷固定来判断褶皱形成,但径向位移并不是一个反映身管材料变形的本质物理量,因此需要进一步地探究以找到与这种现象相关的本质,为了定量描述褶皱的形成,引入了一个指标,即在下沉段的半径减小量Y,如图4所示。Y可通过下式计算:
Y=mΔh
(1)
Δh=vTtanα
(2)
式中,m为锤头锻打的次数;Δh为每次锤头锻打后工件的半径缩减量。
当褶皱形成时,此刻的半径缩减量为Yc,根据褶皱的形成过程,形成如下的褶皱成形判据:
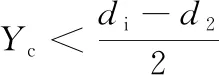
(3)
Yc可以在三维有限元模型中根据褶皱的波峰波谷固定不再转移到其他节点时确定,而di是毛坯的内径,d2是锻后身管的内径,也就是身管的口径。如果Yc比(di-d2)/2小,则说明该锻件在下沉段结束前一定会产生褶皱。
选择径向精锻实验来验证上述褶皱成形判据,根据表4的工件尺寸建立三维有限元模型,提取下沉段内壁节点的径向位移,根据式(3)褶皱形成判据,得出波峰波谷固定时对应的半径减少量Yc,褶皱是否能形成的预测如表6所示。对于L1试件,仿真结果显示当褶皱形成时,半径减小量Yc为0.802 mm,大于整个下沉段的半径减小量0.65 mm,这表明在褶皱形成之前,L1试件的内壁已接触芯棒,完成了下沉段,进入了锻造段。仿真得出的L2和L3试件的褶皱形成时的半径减小量Yc均小于整个下沉段的半径减小量,这表明在褶皱形成时,下沉段还没有结束,工件内壁接触芯棒之前形成了褶皱。
对锻后身管内膛进行电镜观察,如图13~图15所示,其中,位置1是毛坯的内壁形貌,位置2是下沉段刚结束时的内壁形貌。

图13 L1试件的内壁形貌

图14 L2试件的内壁形貌

图15 L3试件的内壁形貌
图13所示为L1身管下沉段结束时内膛形貌,可以看出,内膛表面比较粗糙,但是没有找到沿轴向分布明显的褶皱,这说明L1身管在下沉段结束时没有产生褶皱,与预测结果一致。
图14所示为L2身管下沉段结束时的内膛形貌,可以清晰地看到,有沿轴向的褶皱,另外在图14中还发现了许多横向的条纹,这是由于L2身管毛坯内孔是由高速车削加工的,横向的条纹是刀纹,与锻打产生的褶皱无关。L2身管下沉段结束时褶皱已经成形,与根据褶皱判据做出的预测结果一致。
图15所示为L3身管下沉段结束时的内膛形貌,可以看到明显的沿轴向分布的褶皱,并且其褶皱形貌比图14中L2身管的褶皱形貌要清晰,这说明L3身管内膛在接触芯棒前褶皱就形成了,与预测结果一致。
4.3 工艺参数对褶皱形成的影响
获得工艺参数对褶皱形成的影响规律有助于控制褶皱缺陷。根据表7中的工艺参数设置,模拟了多个参数的径向锻造过程,每个模拟算例仅改变一个工艺参数。这些工艺参数下褶皱形成的判据如表7所示。
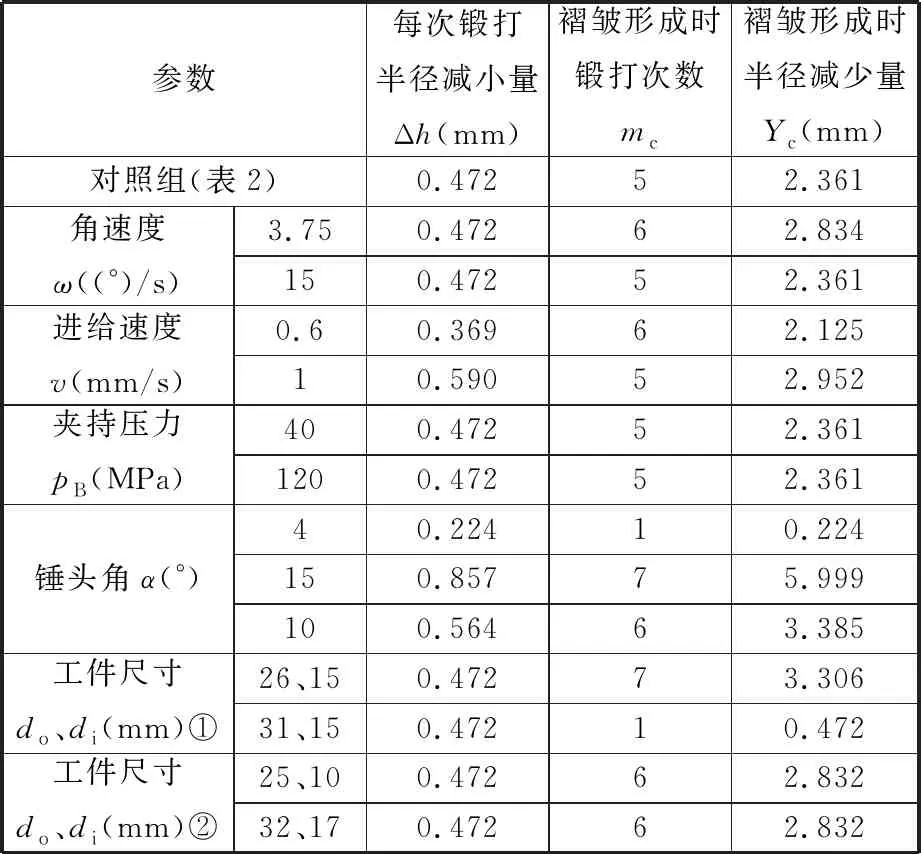
表7 不同工艺参数下褶皱成形判据值
比较上述工艺参数下的Yc值来研究工艺参数对褶皱形成的影响并不是很直观,因此引入ΔY来表示褶皱形成的难易程度,该值表示褶皱形成时的工件半径减少量比设计的全下沉段的半径减少量小多少,越小说明褶皱形成得越早,ΔY越小,该工艺参数越容易形成褶皱,ΔY计算式如下:
(4)
由式(4)可以看出,ΔY可能为负值,ΔY越大,说明形成褶皱时的半径缩减量越大,形成褶皱的难度越大,径向锻造成形身管的质量越好。
每次锻打的半径缩减量Δh只与轴向进给速度、锤头的纵截面角α和一次锻造周期有关。在实际锻造过程中,每次锻打的周期通常是固定的,因此,本文不涉及锻打周期变化的模拟。为了直观地比较褶皱成形判据Yc和褶皱形成难易程度ΔY在不同工艺参数下的变化,将结果绘制为线图。
主轴角速度变化下Yc和ΔY的变化如图16所示,由于锤头布局的对称性,故所选的三个转速在一个锻打周期内工件旋转的角度为15°、30°及60°,均在90°以内,从图16中可以看出主轴角速度对褶皱形成的影响不明显,尽管Yc值在3.75°/s时有波动,此时褶皱成形时对应的Yc为2.834 mm,锻打了6次,接近其他两个不同的主轴角速度下褶皱形成时Yc的值(2.361 mm),以及锻打的次数(5次),有限元计算的误差可能导致这种差异,因此近似认为主轴角速度对褶皱的形成无影响。
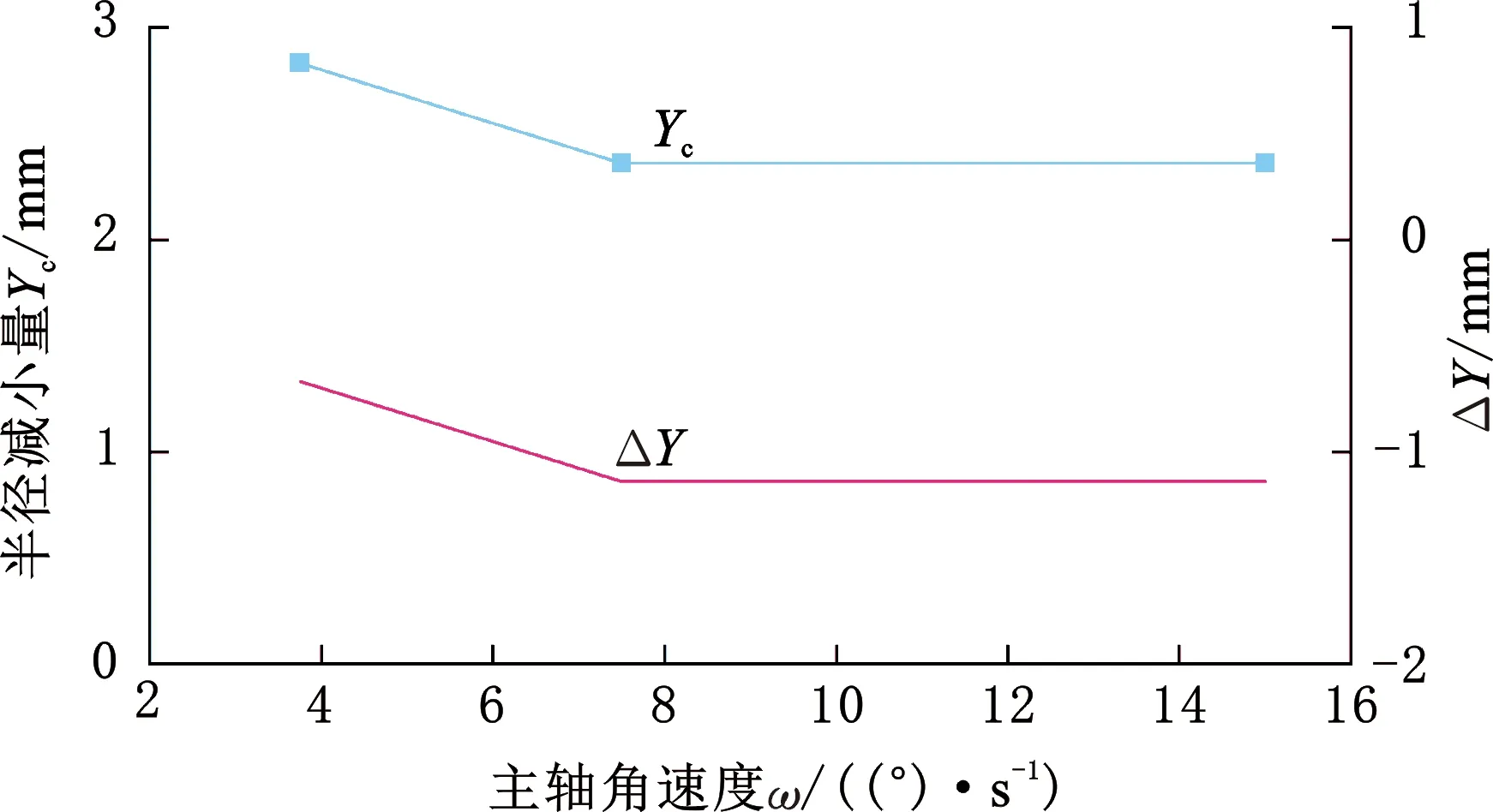
图16 不同角速度下褶皱形成时的Yc和ΔY
图17所示为进给速度对褶皱形成的影响,可以看出,Yc和ΔY都随着进给速度的增大而增大,进给速度为1 mm/s时对应的Yc比0.6 mm/s的值大38.92%,这表明轴向进给速度对褶皱缺陷的形成有影响,轴向进给速度越大,褶皱形成时的半径缩减量越大,褶皱越难形成。
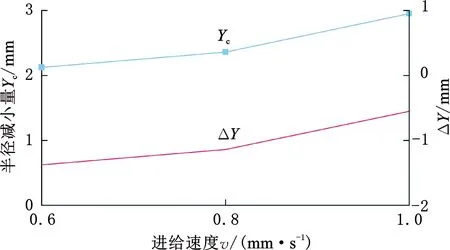
图17 不同进给速度下褶皱形成时的Yc和ΔY
对于夹持压力,如图18所示,改变夹持压力后,褶皱形成时Yc和褶皱形成难易程度ΔY并没有变化,这说明夹持压力对褶皱缺陷的形成时刻没有影响。

图18 不同夹持压力下褶皱形成时的Yc和ΔY
锤头的纵截面角α对褶皱的形成影响很大,改变锤头角α会改变每一锤对应的半径减小量Δh,如图19所示,仿真设计了4个锤头角度的算例,随着角度的增加,Yc和ΔY越来越大,这种影响规律接近线性增长。当α=4°时,第一次锻打时褶皱就形成了,对应的Yc为0.224 mm,ΔY为-3.276 mm。当α=15°时,褶皱形成时Yc为5.999 mm,ΔY为2.499 mm。由上可知,锤头角度越大,褶皱形成的可能性越小。上述规律与童维等[12]的研究类似,他们采用形貌测量研究了下沉段褶皱的增长情况,发现锤头角度越大,内膛节点下沉段应变比越小,而应变比与褶皱形貌高度增长成正比,也就是锤头角度越大,褶皱增长得越慢,尽管本文研究的是褶皱形成的时刻,形成之后才能增长,但是和他们的研究一样,都得出了锤头角度是影响褶皱的重要工艺参数,并且增大锤头角度有利于控制褶皱的结论。

图19 不同锤头角时褶皱形成时的Yc和ΔY
保持内径不变改变工件外径,工件越厚,褶皱越容易形成,如图20所示,随着厚度t的增大,Yc和ΔY逐渐减小。厚度为5.5 mm时,褶皱形成时的Yc值为厚度为9.5 mm时的Yc值的7倍,厚度为9.5 mm时在第1锤就形成了褶皱。

图20 不同厚度工件褶皱形成时的Yc和ΔY
如图21所示,在保持厚度不变但改变内径的情况下,褶皱形成时的半径缩减量Yc没有明显的差别,这并不是说明内径变化对褶皱形成无影响,实际上Yc并不适用于内径改变的情况,因为褶皱是否形成还需要与下沉段半径缩减量(di-d2)/2比较才能确定,改变内径实际上就是改变了di的值,因此单纯地比较不同内径下Yc的值是不准确的,需要用ΔY来评价。对于只改变内径这个工艺参数,Yc与ΔY并没有相同的趋势。内径为10 mm时,ΔY为1.832 mm,而17 mm内径对应的ΔY为-1.668 mm,ΔY随着内径的增大而减小,这种变化的趋势近似于线性,内径越大,褶皱越容易形成,这与常规的认知符合。实际上现在折衷采用的纯线膛精锻工艺其毛坯内径也是会比芯棒直径大约1~2 mm,也就是说理论上纯线膛精锻也存在微小的下沉段,但是纯线膛径向精锻工艺生产的身管内膛并没有发现有褶皱,说明小内径不易产生褶皱。
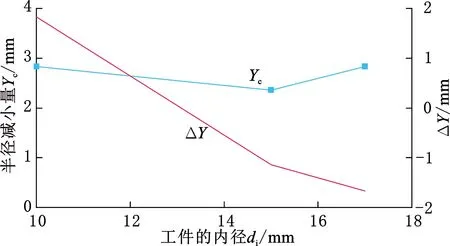
图21 不同内径工件褶皱形成时的Yc和ΔY
综上所述,锤头的纵截面和工件的尺寸对褶皱的形成有显著影响。锤头的纵截面与褶皱形成时的半径减小量Yc和褶皱形成的难度ΔY成正相关,锤头角越大,Yc和ΔY越大,褶皱越难形成;内径不变,工件厚度越大,Yc和ΔY越小,褶皱越容易形成;而工件的厚度不变改变内径时,内径越大,ΔY越小,褶皱越容易形成;主轴角速度和夹持压力对褶皱的形成没有明显的影响;轴向进给速度对褶皱形成的影响较小,成正相关趋势。上述规律暂时无法通过实验验证,因为在实际径向锻造过程中难以检测凹陷区域中皱纹形成的时间,然而童维等[12]通过二维有限元以及下沉段褶皱形貌测量也发现了锤头角度以及工件尺寸对褶皱的形貌影响最大,与本文得出的影响最大的工艺参数一致。
5 结论
(1)利用三维精锻有限元模型推得下沉段褶皱产生的机理:由于相邻锤头之间存在间隙,导致锻打时身管横截面径向受力不均匀,从而引起变形不均匀,相邻节点的径向位移差就是褶皱的高度,在持续锻造后,这种不均匀的径向变形累积并导致在内壁上形成轴向褶皱。
(2)下沉段褶皱缺陷的成形判据是:当同一横截面内壁节点径向位移曲线上的峰谷固定在某些节点上并且不随工件的旋转进给移动时,褶皱形成。此时工件的半径减小量Yc被用作定量描述成形判据的指标。通过径向锻造实验验证了成形判据的正确性。
(3)对褶皱形成影响最大的工艺参数是锤头角度和工件尺寸。锤头角度越大,毛坯厚度越小,毛坯内径越小,则褶皱形成越晚,对生产越有利。工件旋转速度、进给速度、夹头夹持力等工艺参数对褶皱的形成影响较小。
