基于过程阻尼的钛合金丝材表面车削精整加工稳定性研究

2023-09-06史丽晨刘腾飞刘亚雄卢竹青

中国机械工程 2023年16期

史丽晨张倩刘腾飞刘亚雄卢竹青

1.西安建筑科技大学机电工程学院,西安,7100552.西部超导材料科技股份有限公司,西安,710018

0 引言

钛及钛合金材料由于具有比重小、比强度高、耐蚀性好及耐高温等特点,已广泛应用于制造生产航空航天领域的紧固件。通常航空航天紧固件制备用钛合金丝材坯料的要求为单根质量不小于100 kg,即φ8 mm的钛合金丝材长度将达到600 m左右,且对加工后的尺寸精度和表面精度的要求也极高,通常尺寸公差不大于0.02 mm,表面粗糙度度值Ra≤1.6 μm。这就对钛合金丝材表面精整加工技术提出了更高的要求,要求系统连续工作时间长、加工系统稳定性好、精确度高。

表面精整加工是一种精密加工的方法,通过去除极薄的材料表面层来实现提高尺寸精度和降低表面粗糙度的目的[1]。通常表面精整加工方法有研磨和珩磨,但其加工效率低,环境污染大,且对坯料尺寸有限制要求[2-3]。国外现多采用表面车削精整加工方法,可在满足表面加工质量的前提下显著提高加工效率和减少环境污染。无心车床是一种常用的表面车削精整加工设备,它不仅可以通过车削去除表层极薄的材料来实现对钛合金丝材盘圆的精整加工,也可以车削去除管棒丝材表面裂纹、表面氧化皮和其他表面缺陷,同时降低表面粗糙度并提高尺寸精度[4]。由于无心车床结构的特殊性,理论上它可以实现无限长丝材的表面精整加工。对于小直径大盘卷钛合金丝材的表面精整车削,由于钛合金的难加工性,且坯料直径极小,无心车床加工过程中极易发生切削颤振和加工变形,严重影响了加工后的尺寸精度和表面质量[5-6]。因此,本文以提高无心车床刀盘切削系统稳定性为目的,研究无心车床表面车削精整加工颤振机理,这对抑制刀盘切削系统的颤振、提高加工质量十分必要。

近年来,许多学者通过建立颤振动力学模型来分析切削稳定性,并取得了丰硕的成果。邱辉等[7]以数控车床为研究对象,考虑颤振形成机理,建立单自由度动力学模型,分析结构振动参数变化对稳定性叶瓣图的影响。李勤良等[8]以普通正交车削为研究对象,建立考虑非线性迟滞力和激振力的单自由度颤振模型,利用稳定性叶瓣图进行稳定性分析,得到主轴转速、切削深度以及滞回参数对颤振振幅的影响规律。OZLU等[9]以普通车削为研究对象,建立考虑刀片刀尖半径的单自由度切削系统颤振动力学模型进行稳定性分析。仇健[10]以数控车床为研究对象,建立考虑工件轴向和径向两个方向刀具刃倾角和模态方向的切削颤振模型进行切削稳定性判断,肯定了稳定性叶瓣图的判断结果。以上主要是针对普通车床以及数控车床进行切削颤振的多方面研究,但对具有特殊结构的表面车削精整加工设备——无心车床的研究较少;同时在进行颤振模型稳定性分析时,刀具结构参数对车削精整加工时的稳定性也有直接影响,研究时需一并考虑。

钛合金材料由于其固有特性[11-13],在高速切削时会加速刀具磨损且极易发生黏刀现象,无法满足降低表面粗糙度和提高尺寸精度的要求,因此在无心车床车削颤振模型建立时,应当考虑低速切削的影响。针对低速切削工况,李亮等[14]考虑过程阻尼建立非线性铣削动力学模型并计算稳定性极限。李忠群等[15]考虑过程阻尼的影响建立单自由度切削动力学模型,分析了稳定性极限值。秦国华等[16]考虑过程阻尼建立两自由度铣削动力学模型,分析了参数变化下稳定区域的变化规律。以上研究肯定了低速切削工况下考虑过程阻尼的必要性,考虑到无心车床进行钛合金丝材表面精整加工过程的低速切削特性,研究时需考虑过程阻尼的影响。

综上,本文以表面车削精整加工设备——无心车床的刀盘切削系统为研究对象,在分析其结构工作原理和刀盘切削系统结构特性的基础上,建立考虑过程阻尼效应的多自由度耦合颤振动力学模型。基于颤振动力学模型绘制稳定性叶瓣图进行稳定性分析,得到表面精整加工的稳定可加工参数组选择域,继而在分析刀具结构参数对切削稳定性的影响的基础上,确定稳定加工的刀具结构参数选择域,最后通过试验进行验证。

1 无心车床切削系统动力学模型

1.1 无心车床切削系统结构介绍

本文采用图1所示的无心车床完成对难加工材料钛合金丝材盘圆的表面车削精整加工。车床由夹送系统、导向系统、刀盘切削系统以及主轴箱组成。

(a)结构示意图

(b)加工原理示意图图1 无心车床结构图

在车削加工时,闭合前导向,钛合金丝材经外部传送机构进入图1a所示的前夹送,前夹送中的辊轮装置带动丝材持续做直线进给运动,使其通过前导向进入刀盘切削系统,装有刀具的刀盘切削系统绕丝材持续做回转切削运动,加工后的丝材通过中后导向被送出主轴箱,再经后夹送中的辊轮装置持续抽离,使丝材离开无心车床,以完成对丝材的表面车削精整加工。

图2为无心车床刀盘切削系统结构图,该系统由起支撑作用的刀盘以及镶嵌在刀盘燕尾槽的四个装有刀具的刀盒和四个起固定刀盒作用的压块装配而成,在装配时刀盒的切向位置由压块进行固定,径向位置由刀盘切削系统的外围进行固定。

图2 无心车床刀盘切削系统结构图

1.2 模型建立

对无心车床刀盘切削系统的结构进行分析,考虑刀盒在径向的颤振位移以及在切向的滑动位移,基于达朗贝尔原理,考虑过程阻尼效应,建立关于无心车床刀盘切削系统的多自由度耦合颤振动力学模型,如图3所示。

图3 无心车床刀盘切削系统动力学模型

根据无心车床刀盘切削系统的结构特点,对模型作出如下假设:①整个刀盘切削系统由四个小系统组成,分别是以刀盒1为主刀盒3为辅,刀盒2为主、刀盒4为辅,刀盒3为主、刀盒1为辅,刀盒4为主、刀盒2为辅;②刀盒1、2、3、4的固有特性一致,压块1、2、3、4对刀盒的影响均相同,刀盘切削系统内部颤振位移L3r与L1r等大反向。

考虑刀盘切削系统的弹性恢复力和各自方向上的位移成正比,阻尼力和各自方向的振动速度成正比,以动力学模型中丝材集中质量的平衡位置为坐标原点,根据力的平衡关系建立无心车床切削系统的动力学方程:

(1)

式中,m1、m2、m3、m4分别为装有刀具的刀盒1、2、3、4的等效质量;c1r、c2r、c3r、c4r分别为刀盒1、2、3、4在径向上的等效阻尼;c1a、c2a、c3a、c4a分别为刀盒1、2、3、4在轴向上的等效阻尼;k1r、k2r、k3r、k4r分别为刀盒1、2、3、4在径向上的等效刚度;k1a、k2a、k3a、k4a分别为刀盒1、2、3、4在轴向上的等效刚度;L1r、L2r、L3r、L4r分别为刀盒1、2、3、4在径向上的振动位移;L1a、L2a、L3a、L4a分别为刀盒1、2、3、4在轴向上的振动位移;Fr、Fa分别为刀盘切削系统在刀盒径向和轴向上的切削力。

考虑过程阻尼效应(即刀具后刀面与工件之间的干涉作用),它所产生的犁耕力大小取决于刀具与工件之间形成的压痕体积[17-18]。而车削加工的过程中,由于车削加工前的钛合金丝材盘圆原始表面粗糙度呈上下起伏无规律变化,当刀具位置固定后,车削过程中刀具刀尖嵌入丝材的体积大小随着车削位置的变化发生非线性变化。为便于研究,将非线性过程阻尼系数等效为一个线性的过程阻尼系数。在一个切削周期内由等效过程阻尼消耗的总能量等于由刀具压入工件作用产生犁耕力所消耗的能量,由此构建非线性过程阻尼系数与等效过程阻尼系数之间的数学关系[19],其表达式如下:

(2)

式中,ceq为过程阻尼系数;ksp为压痕系数;ap为切削深度;W为刀尖磨损宽度;v为切削速度;kγ为刀具主偏角。

式(2)中,压痕系数ksp[20]和刀尖磨损宽度W[21]可分别表示为

(3)

W=rεsinβ+rεsinγ+rε(cosγ-cosβ)cotγ

(4)

式中,E为材料弹性模量;ρ为刀具的变形程度;μ1为泊松比;rε为刀尖圆弧半径;β为刀具前角;γ为刀具后角。

将式(3)和式(4)代入式(2)可以得到过程阻尼系数的等效关系式:

(5)

由于犁耕力的产生,无心车床刀盘切削系统的切削力F可以被表示为动态切削力Fs与犁耕力Fp之和,即

(6)

式中,b为切削宽度;kf为切削刚度系数;h为切削厚度;μ为库仑摩擦力因数;h0为理论切削厚度;T为机床主轴旋转一周所用时间;L(t)为t时刻下刀具的振动位移;L(t-T)为t-T时刻下刀具的振动位移。

1.3 理论计算分析

整理无心车床刀盘切削系统动力学方程,以刀盒1为主、刀盒3为辅的小系统为例,如图4所示,得到刀盒切削系统动力学方程:

(7)

图4 刀盒动力学模型

对式(7)做拉普拉斯变换,得到如下变换式:

(8)

式中,s为拉普拉斯算子;ξ为阻尼率;ωn为固有频率。

将式(8)整理成如下矩阵形式:

(9)

令式(9)矩阵的行列式等于零,求解方程组的非零解,得到

(10)

使用特征方程的根来判定系统的稳定性:当特征方程根的实部大于0时,切削系统处于不稳定状态;当特征方程根的实部小于0时,切削系统处于稳定状态;当特征方程根的实部等于0时,切削系统处于稳定和不稳定之间的临界状态。将临界状态下的s=jω代入式(10)并且进行整理,令特征方程的实部和虚部分别等于0,可得

(11)

其中,ω为车削振动系统的颤振频率。联立式(11)和主轴转速的定义式n=60/T,得到关于无心车床刀盒切削系统主轴转速的表达式为

(12)

同时,由式(11)中实部为0的公式推导得到无心车床刀盒切削系统极限切削深度的数学表达式为

ap=A0k1asinkγ

(13)

A0=

2 无心车床刀盘切削系统稳定性影响规律分析

2.1 稳定性分析

采用有限元计算的方法来获取模态参数[22],建立刀盘三维模型并对其进行有限元分析,其结果如表1所示,材料参数设置如表2所示。

表1 刀盘系统模态分析结果

表2 刀盘材料参数设置

根据刀盘材料设置参数以及式(3),可以得到无心车床刀盘切削系统的压痕系数ksp为4.36×105N/mm3。同时,使用抗振性较好的YG8硬质合金刀具进行钛合金丝材盘圆的表面车削精整加工,刀具的相关参数如下:前角β=2°,后角γ=7°,刃倾角0°,主偏角30°,刀尖圆弧半径rε=0.3 mm[23]。根据选用刀具的结构参数以及式(4),可以得到无心车床刀盘切削系统的刀尖磨损宽度W为0.03 mm。

采用稳定性叶瓣图来完成无心车床刀盘切削系统切削加工的稳定性分析,稳定性叶瓣图呈现形式是一个以主轴转速为横坐标、以极限切削深度为纵坐标的曲线图,曲线之上为不稳定区域,曲线之下为稳定区域[24]。

考虑到工程实际中无心车床加工钛合金丝材盘圆对进给速度的要求较高,故选定进给速度为1000 mm/min进行稳定性分析。根据理论推导得到的无心车床刀盘切削系统动力学模型的理论结果(式(12)和式(13))以及有限元计算得到的模态参数,绘制无心车床刀盘切削系统稳定性叶瓣图,见图5。

图5 无心车床刀盘切削系统稳定性叶瓣图(β=2°,γ=7°,rε=0.3 mm)Fig.5 Stability lobe diagram of the cutter head cutting system of the centerless lathe(β=2°,γ=7°,rε=0.3 mm)

观察稳定性叶瓣图可以发现高主轴转速下的叶瓣褶皱十分疏散,而低主轴转速下的叶瓣褶皱十分密集,说明相较于高主轴转速,低主轴转速下可选择的稳定可加工参数组的数量减少。同时低主轴转速下由于叶瓣褶皱密集,褶皱间可选择的稳定可加工参数区域收窄,在实际加工中极易超出临界曲线,进入不稳定区域,进而发生颤振,这说明低主轴转速切削状态下的切削稳定性较差。

考虑工程实际中无心车床进行钛合金丝材盘圆表面车削精整加工时的加工参数选择范围,将横坐标主轴转速范围限定在300～900 r/min,绘制图5中所示的细节图。将稳定性叶瓣图分为两个部分讨论:①图中曲线以上(即A点所在区域)为不稳定区域,此区域没有可选择的稳定可加工参数组;②图中曲线以下(即B点所在区域)为稳定区域,工程实际中在此区域内进行稳定可加工参数组的选取。同时,经观察发现,图中曲线所对应极限切削深度的最小值为0.4435 mm,且每个叶瓣的最小值保持一致,故稳定区域包含一个绝对稳定区域,在此区域内随机选择加工参数,无心车床都不会发生颤振。

2.2 刀具结构参数对切削系统稳定性的影响规律分析

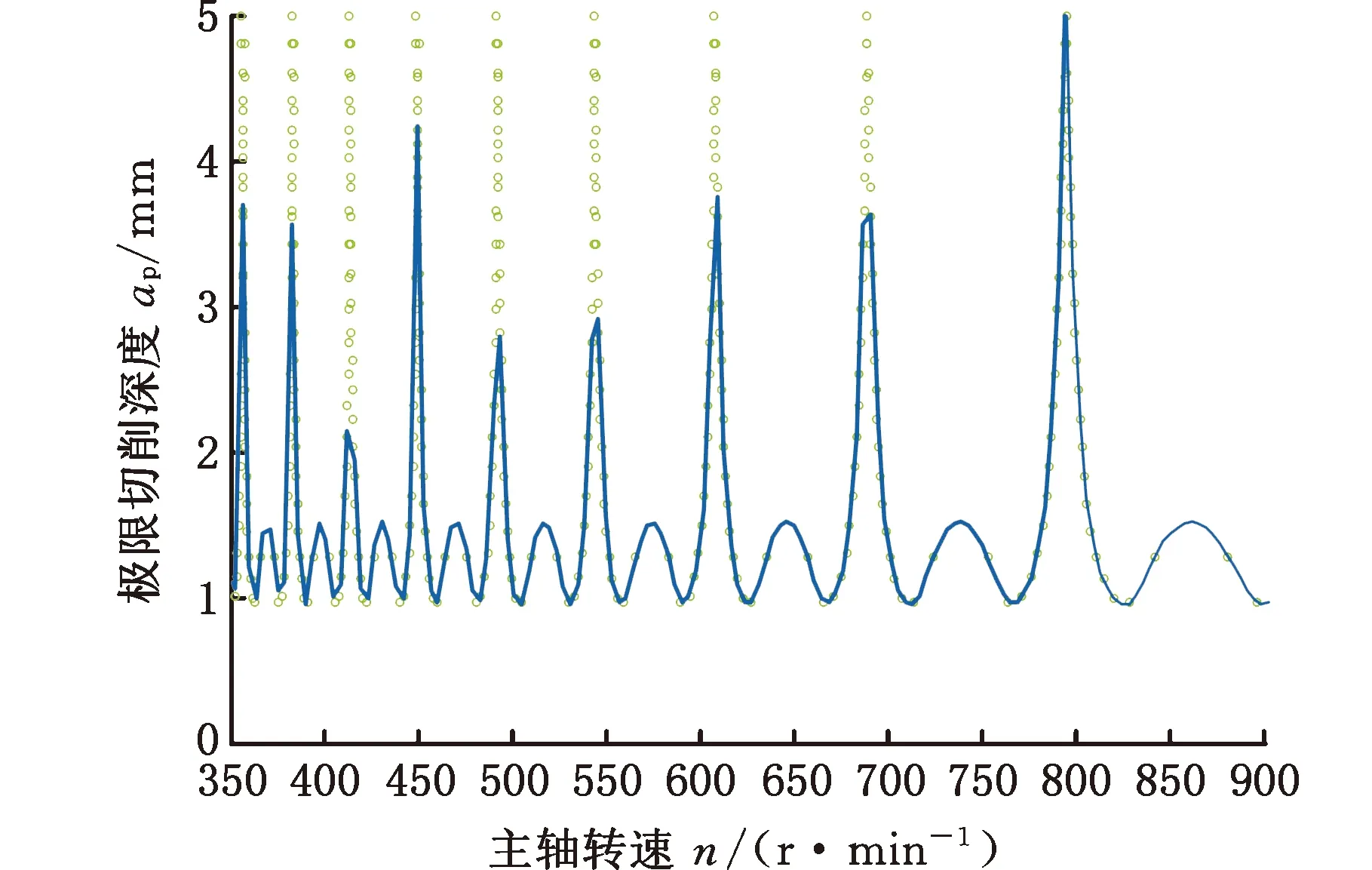
刀具是无心车床刀盘切削系统里面的核心部件,观察式(5)可以发现,过程阻尼系数与刀具的刀尖圆弧半径以及前角、后角之间都存在关系。选定进给速度为1000 mm/min,绘制刀尖圆弧半径、刀具前角和后角变化下的稳定性叶瓣图,分别见图6～图8,研究刀具结构参数对无心车床刀盘切削系统稳定性的影响规律。

(b)rε=0.3 mm

(c)rε=0.5 mm

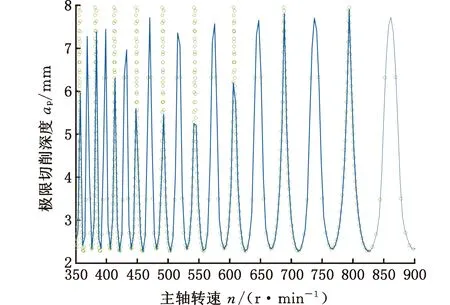
(d)rε=0.8 mm图6 刀尖圆弧半径影响下的稳定性叶瓣图(β=2°,γ=7°)Fig.6 Stability lobe diagram under the influence of tool tip arc radius(β=2°,γ=7°)

(a)β=1°

(b)β=2°

(c)β=5°

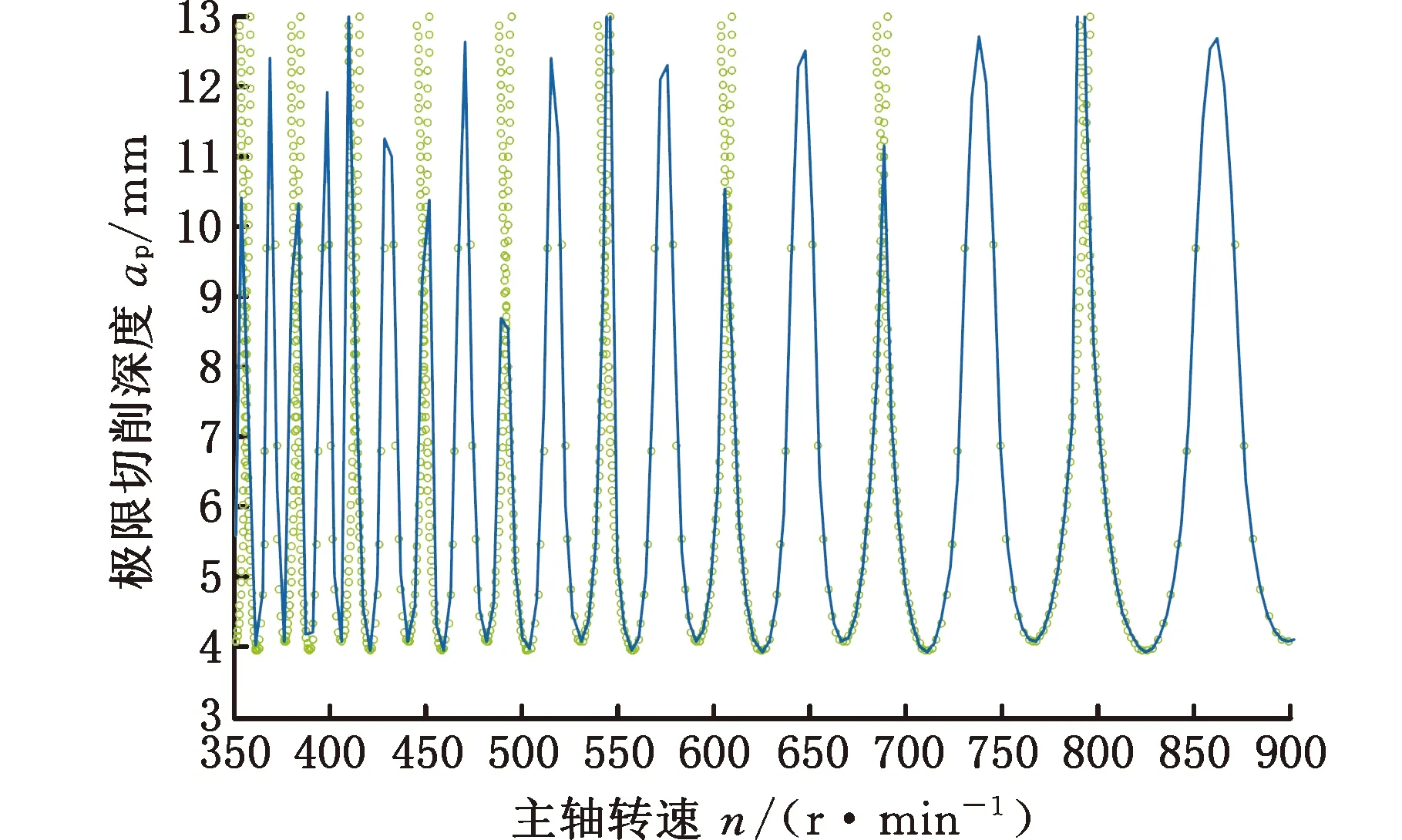
(d)β=7°图7 刀具前角影响下的稳定性叶瓣图(rε=0.3 mm,γ=7°)Fig.7 Stability lobe diagram under the influence of tool rake angle(rε=0.3 mm,γ=7°)

(a)γ=2°

(b)γ=5°

(c)γ=7°

(d)γ=10°图8 刀具后角影响下的稳定性叶瓣图(rε=0.3 mm,β=2°)Fig.8 Stability lobe diagram under the influence of tool clearance angle(rε=0.3 mm,β=2°)

观察图6所示刀尖圆弧半径变化下的稳定性叶瓣图发现,当刀尖圆弧半径过小时(图6a),稳定性叶瓣图呈现不规律变化,工程实际中可选择的稳定可加工参数组较少,工作效率低且极易发生不稳定颤振现象,设计安全性较低。而随着刀尖圆弧半径的增大,如图6c和图6d所示,观察发现在同一个主轴转速变化区间内,稳定性叶瓣图的叶瓣数量逐渐增多且临界稳定切削深度的最小值发生上移,工程实际中可以选择的稳定可加工参数增多,但由于叶瓣间的褶皱非常密集,在切削加工过程中极易进入不稳定区域而发生颤振,加工稳定性极差,设计安全性较低。综上,在进行无心车床刀盘切削系统刀具结构设计时,应选择刀尖圆弧半径rε在0.1～0.3 mm之间,此时具有较高的设计安全性以及加工稳定性。

观察图7和图8所示刀具前角和后角影响下的稳定性叶瓣图发现,随着刀具前角和后角的增大,稳定性叶瓣图临界稳定切削深度的最小值逐渐增大,稳定性叶瓣图呈现逐步上移的变化趋势,绝对稳定区域面积增大。同时,观察发现在同一个主轴转速变化区间内,随着刀具前角和后角的增大,稳定性叶瓣图的叶瓣数量逐渐增多,稳定可选择加工参数组增多。但随着叶瓣图中的叶瓣数量的增多,叶瓣间的褶皱逐渐密集,在加工过程中极易越过临界稳定曲线进入不稳定区域而发生颤振,加工稳定性极差,设计安全性较低。综上,在进行无心车床刀盘切削系统刀具结构设计时,应选择刀具前角β在1°～2°之间,刀具后角γ在2°～5°之间,此时具有较高的设计安全性以及加工稳定性。

3 试验验证

基于上述理论分析,为验证无心车床过程阻尼效应下多自由度耦合颤振动力学模型的正确性,进行试验设计,对模型进行验证。

3.1 试验条件

根据工程实际需求,选取试验材料为TB9丝材盘圆,材料的直径为8 mm,来料为热拉拔后未经热处理。根据刀具结构参数对切削系统稳定性的影响规律分析结果,选用的切削刀具为 YG8 硬质合金刀具,该刀具的前角为2°、后角为3°、刀尖圆弧半径为0.3 mm。

根据图9所示的稳定性叶瓣图,在图上以临界曲线所在位置为参考,设置共9组试验参数点,进给速度设置为1000 mm/min。为减小试验误差,加工长度均取1300 mm,在试切300 mm后进行试验方案加工,设定试切的300 mm为非观察区间,并观察试验后的工件表面状态。

采用时代TR2000表面粗糙度仪在表面车削精整加工结束后对观察区间进行表面粗糙度的测量,对观察区间表面等距选取3个测量点,每个测量点顺时针旋转120°,对3个测量点的表面粗糙度取均值,即认定为该组工艺参数下的表面粗糙度。

振动信号采用北京东方振动和噪声技术研究所研发的 DASP 智能数据采集和信号分析系统。采样频率设置为1024 Hz,搭建振动试验平台如图10所示。

图9 稳定性叶瓣图验证试验

3.2 稳定性分析

图9中各试验参数点所对应的试验参数组与试验结果如表3所示。

取稳定性叶瓣图曲线上方、临界位置以及下方(依次对应B1、B2、B3)进行振动信号时频分析,如图11所示。观察图11,从时域图中可以看出,对于处于不稳定区域的B1点和处于临界位置的B2点,其振动信号波形相比于稳定区域B3点的波形更加波动且振动幅值明显增大;对频谱图继续进行分析可知,分别使用B1点、B2点和B3点试验参数进行切削时,不稳定区域的振动信号对应的频谱图的幅值发生了明显增大,且在频率方向(即横向)发生了偏移,除了无心车床主轴的正常切削频率外,还出现了多种频率,忽略环境因素的影响,判断多种频率是由切削中的颤振所产生的,因此证实了B1、B2点的加工状态为不稳定切削,B3点的加工状态为稳定切削。

表3 试验点参数设置与试验结果

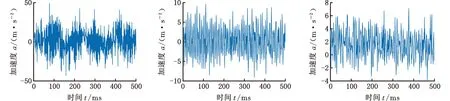
(a)B1点时域图 (b)B2点时域图 (c)B3点时域图

(d)B1点频谱图 (e)B2点频谱图 (f)B3点频谱图图11 振动信号时频分析图

图12给出了非稳态工艺参数组(B1点)和稳态工艺参数组(B3点)加工参数下的工件表面状态,并结合表3中表面粗糙度值Ra的试验结果进行分析。图12a所示为稳态工艺参数组加工后的工件表面状态,可以看出,工件表面光亮,无异常波纹,表面粗糙度值Ra为0.6776 μm;图12b所示为非稳态工艺参数组加工后的工件表面状态,可以明显看出,工件表面存在规律性水波纹,且触感明显,表面粗糙度值Ra为0.9233 μm。同时由表3中的测量数据可以发现,表面粗糙度值随着切削深度的增大而迅速增大,而主轴转速对加工后表面粗糙度的影响较小。