时频能量谱与VGG16结合的车轮扁疤损伤程度估计方法

2023-09-06李大柱梁树林池茂儒

中国机械工程 2023年16期

李大柱牛江梁树林池茂儒

西南交通大学牵引动力国家重点实验室,成都,610031

0 引言

列车在运行中车轮由于空转打滑等原因而造成踏面局部的擦伤和剥离,此现象统称为车轮扁疤[1],扁疤故障是铁道车辆车轮常见的故障形式之一。存在扁疤故障的车轮在行驶中,随着车轮的旋转在轮轨间产生周期性的脉冲激扰,产生的冲击力是正常车轮的数倍[2]。车轮扁疤的出现加剧了轮轨间的冲击力,不仅增加了振动、噪声使乘坐舒适度下降,而且也加速了车辆及轨道零部件的损伤,严重时还会影响行车安全,因此,对列车车轮扁疤状态的实时精确监测对保证列车的运营安全具有重要的意义。智能算法的快速发展使机器学习在图像识别、医学等领域被广泛地应用,近年来也有专家学者将其应用在机械故障的诊断中,尤其是卷积神经网络在机械故障的诊断中深受青睐[3-5]。李恒等[6]将卷积神经网络与短时傅里叶变换结合来诊断轴承故障,此方法对不同类型的故障识别有很高的准确度。孟强斌[7]将卷积神经网络与时频图结合运用在水电机组故障诊断中,大幅提高了故障分类的准确率。张雪嘉[8]将改进的卷积神经网络与经验小波结合运用在风机故障的诊断中,实现了风机故障的快速高效分类。李大柱等[9]将卷积神经网络与多尺度时频图结合运用在铁道车辆车轮故障诊断中,也取得了较高的准确率。相比于传统诊断方法,与卷积神经网络相结合的故障诊断方法不仅效率高而且诊断准确率不受人为因素的影响。现有的智能故障诊断研究中绝大多数是运用卷积神经网络来实现故障分类的。铁道车辆车轮扁疤损伤程度的定量估计对保证列车运营安全、降低维护成本等都有重要的意义,因此,本文提出一种基于VGG16卷积神经网络的车轮扁疤损伤程度估计方法,通过实时采集扁疤车轮所在轴箱的垂向振动加速度来实现对车轮扁疤损伤程度的定量估计。

1 车轮扁疤故障仿真

1.1 车辆轨道刚柔耦合仿真模型的建立

要研究在车轮扁疤工况下车辆轴箱振动加速度的响应,需在多体动力学的基础上建立完整的车辆模型来进行仿真计算。在一般车辆动力学性能研究中,为简化模型,惯性部件都作为刚体处理,但由于车轮扁疤的产生使轮轨间的相互作用发生改变,所以需要考虑车轮与轨道振动之间的耦合,而车辆-轨道耦合动力学模型恰好是研究车辆与线路相互作用的理论工具[1]。本文以某型国产动车组和我国典型无砟轨道为研究对象,联合ANSYS和Simpack建立了车辆轨道刚柔耦合动力学仿真模型,如图1所示。

图1 车辆轨道刚柔耦合动力学模型

1.2 车轮扁疤数学模型

新扁疤近似于轮周上的一段弦,如图2中弦AB所示,由于新扁疤在轨道上滚动时,扁疤棱角处与轨道产生较大的冲击载荷,扁疤的棱角很快被磨平演变为图2中弧A1OB1,称为旧扁疤。车轮滚过新扁疤位置的过程中,轮心距离轨面的高度先降低后升高,轮心距离轨面高度的变化量计算式如下[10]:

(1)

(2)

式中,Δr为轮心距离轨面高度的变化量;R为车轮滚动圆半径;d为扁疤深度;l0为新扁疤长度;φ为扁疤内夹角;β为车轮滚过的角坐标。

图2 扁疤车轮数学模型

随着车辆的运行,车轮上新扁疤的棱角很快被磨圆演变为旧扁疤,旧扁疤可以用简单的余弦函数来表达,旧扁疤工况下轮心距离轨面的高度变化量计算式如下[10]:

(3)

(4)

式中,x为轮周表面弧长;l为旧扁疤长度。

扁疤表面不同位置与轨面接触时,轮心距离轨面高度的变化量如图3所示,可见,随着扁疤长度的增大扁疤深度逐渐增大,轮心距离轨面的高度变化量也随之增大。

图3 扁疤车轮轮心与轨面距离的变化量

2 形态学滤波与CEEMDAN-WVD时频分析方法

受轨道不平顺等因素的影响,正常车轮所在轴箱的振动加速度信号属于非线性、非平稳信号,车轮扁疤故障的出现又增加了轮轨间间歇的周期性冲击,使车辆轴箱振动加速度信号更加复杂。李奕璠等[11]运用Hilbert-Huang变换(HHT)处理轴箱振动信号,通过Hilbert谱的分布特征来识别车轮多边形故障和扁疤故障。李大柱等[9]也提出通过分析轴箱振动加速度信号的多尺度时频图分布特征来诊断铁道车辆车轮故障。从时域、频域分析轴箱振动加速度只能对车轮故障类型进行识别,要实现对车轮扁疤故障损伤程度的定量估计,需将时域、频域、能量域三者相结合。本文首先采用形态学滤波器对车辆轴箱振动加速度信号进行滤波降噪,然后运用完全噪声辅助集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)与Wigner-Ville 分布(WVD)相结合的时频分析方法将滤波降噪后的信号同时表达在时域、频域和能量域上。

2.1 形态学滤波

线性滤波器对滤除信号中的高斯白噪声成分有较好的效果,但在降噪的过程中也会平滑和模糊一些非平稳信号,如脉冲信号等。非线性滤波器是对输入信号的一种非线性映射,可以将某一特定噪声近似地映射为零,且保留原始信号的主要特征,克服了线性滤波器的不足。车轮扁疤故障引起的轴箱振动加速度信号中包含了大量的冲击成分,属于非线性非平稳信号,不宜采用线性滤波器,因此本文选用形态学滤波器对轴箱振动加速度信号进行滤波降噪处理。形态学滤波器是从数学形态学理论中发展起来的一种新型非线性滤波方法,其工作原理是:根据信号的几何特征,利用预先定义的结构元素对待处理信号进行匹配和局部修正,从而提取信号的边缘轮廓,保持信号的主要形态[12-13]。

2.2 CEEMDAN-WVD时频分析方法

WVD因具有良好的时频聚集性、较高的时频分辨率且可同时反映信号在时域、频域、能量域上的分布特征,而在众多时频分析方法中深受青睐。由于WVD是一种二次时频分布,又不满足可加性,故在处理多分量信号时会产生交叉干扰项,这也是WVD在实际应用中的瓶颈。为了避免WVD在处理多分量信号时产生交叉干扰项,首先将多分量信号分解为单分量信号,然后分别计算各单分量信号的WVD,最后将各单分量信号的计算结果叠加得到多分量信号的时频能量谱。

为抑制WVD交叉干扰项的产生,蔡艳平等[14]提出了经验模态分解(EMD)与WVD相结合的时频分析方法,首先采用EMD将内燃机振动信号分解为若干单分量信号,然后对单分量信号分别进行WVD计算,最后将计算结果叠加得到时频图,根据时频图的分布特征来诊断内燃机的故障。EMD与WVD相结合的时频分析方法在一定程度上抑制了交叉干扰项的产生,但EMD分解存在模态混叠现象,使获得单分量信号的意义不明确。针对该问题,孙国栋等[15]提出了互补集合经验模态分解(CEEMD)与WVD相结合的时频分析方法,并用来诊断滚动轴承故障。CEEMD避免了EMD中模态混叠现象,但未隔离残留噪声,在分解得到的单分量信号中有一定的白噪声残留,影响时频分析结果的准确性。

本文提出CEEMDAN与WVD相结合的时频分析方法来处理车辆轴箱振动加速度信号,得到其在时域、频域、能量域的分布。车辆轴箱振动加速度信号首先经形态学滤波器滤波为x(t);然后运用CEEMDAN将x(t)分解为若干固有模态函数分量(IMF),分解流程如图4所示[16],计算各IMF分量的能量熵增量,并选取能量熵增量相对较大的三阶分量作为主分量[16];最后对各主分量分别进行WVD计算,将计算结果叠加,得到时频能量谱。IMF分量能量熵增量计算如下:

(5)

式中,Cj为CEEMDAN分解后的第j阶分量;E(Cj)为Cj的能量;T为Cj的长度。

对所有IMF分量的能量进行归一化处理:

(6)

计算IMF分量的能量熵增量:

Δqj=-p(j)lgp(j)

(7)

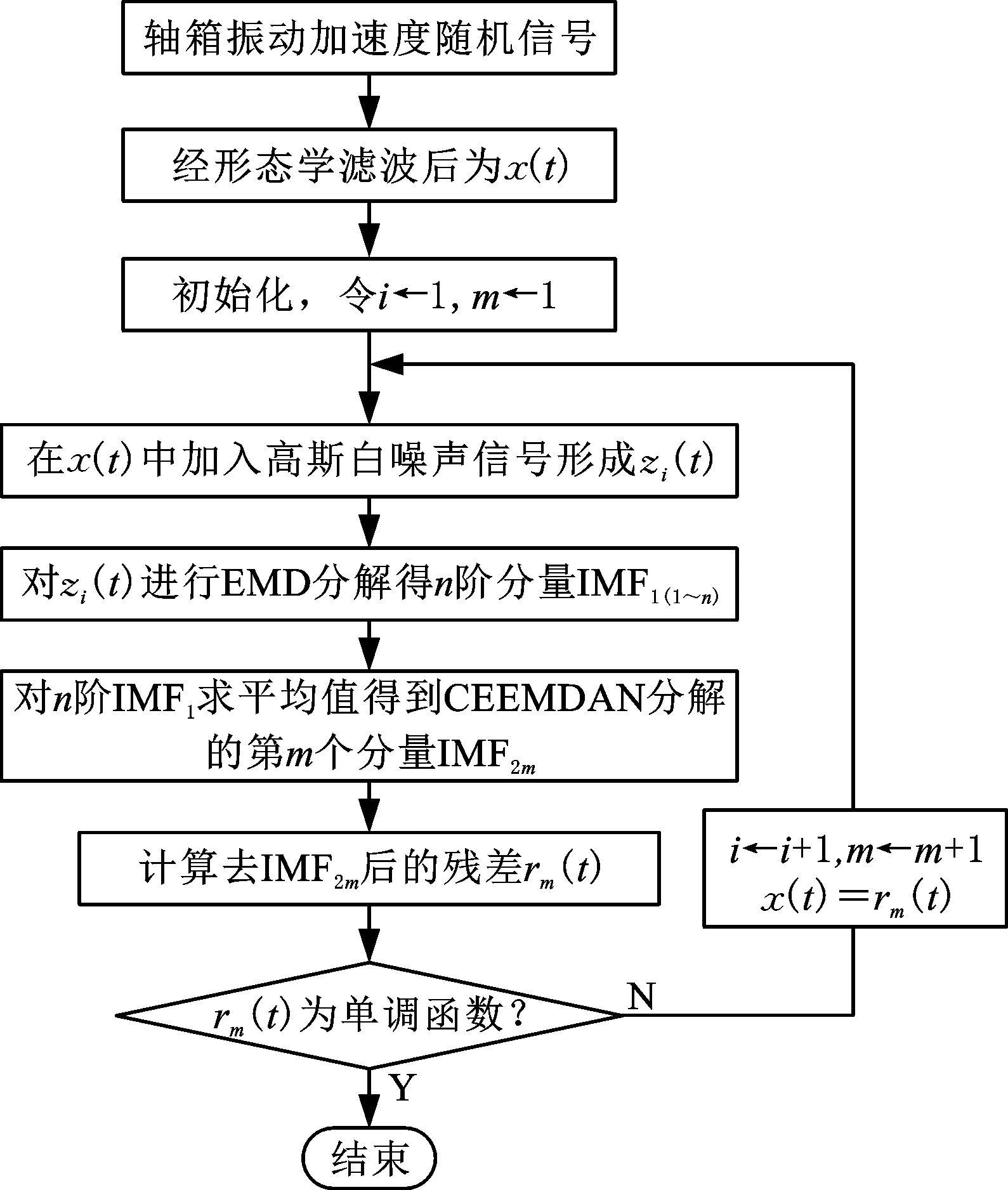
图4 CEEMDAN分解流程图

3 车轮扁疤状态识别

运用提出的形态学滤波结合CEEMDAN-WVD的时频分析方法,对车速为125 km/h、扁疤长度为20 mm的车轮所在轴箱的振动加速度仿真信号进行分析。车轮直径为0.92 m,则该车速下车轮转动频率为12 Hz,扁疤车轮所在轴箱的垂向振动加速度信号如图5所示。轴箱振动加速度原始信号的频谱图见图6a,经形态学滤波处理后的频谱图见图6b。在图6a中,100～300 Hz、400～500 Hz两个频段幅值较为突出,这是施加了线路轨道不平顺造成的,车轮转频相关的频率成分被淹没,从图6a中无法直接识别车轮扁疤故障。图6b中,12 Hz、24 Hz、36 Hz、48 Hz等频率成分较为突出,恰好与车轮转动频率的1倍频、2倍频、3倍频、4倍频相对应。可见通过形态学滤波的方法处理车辆轴箱振动加速度,不仅降低了轨道不平顺等带来的噪声,而且可以有效地提取出车轮扁疤故障引起的与车轮转频及倍频相关的成分。

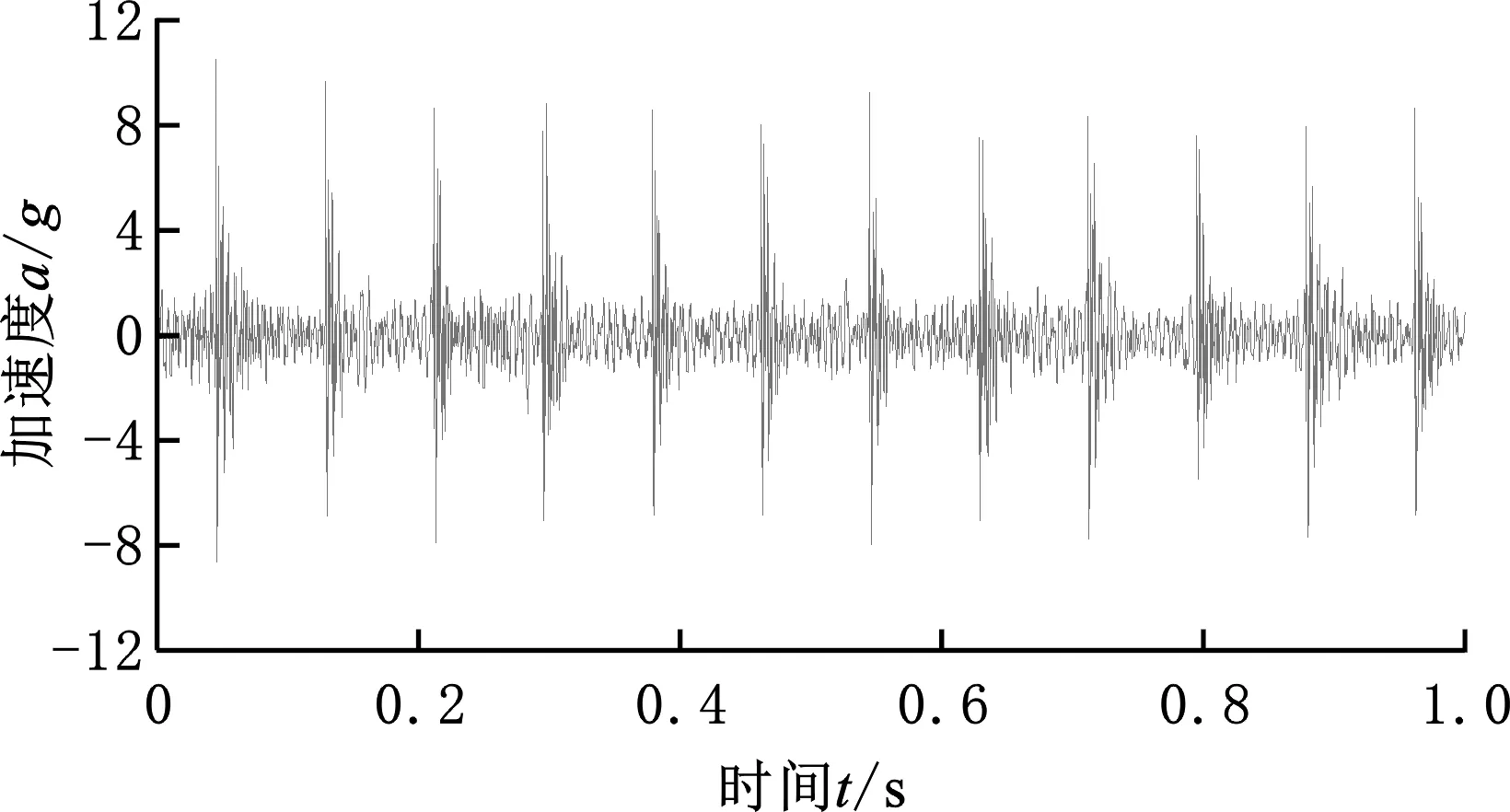
图5 轴箱振动加速度

(a)形态学滤波前

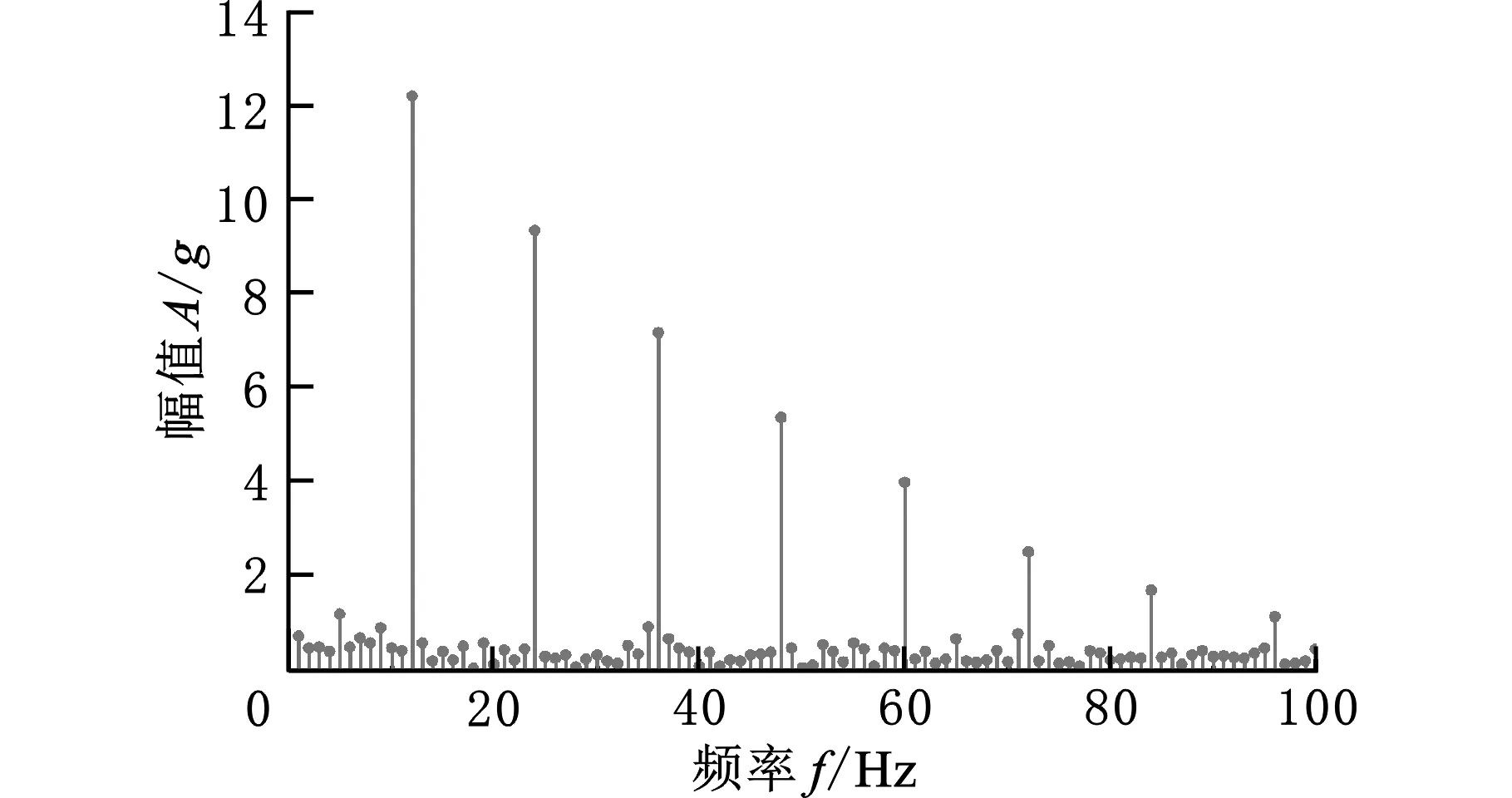
(b)形态学滤波后图6 轴箱振动加速度频谱图

运用CEEMDAN将经形态学滤波降噪后的轴箱振动加速度信号自适应地分解为12阶IMF分量和1阶残余分量,IMF分量时域图见图7。运用式(5)～式(7)计算各阶IMF分量的能量熵增量,结果如表1所示。选取能量熵增量相对较大的IMF7、IMF8和IMF9作为主分量,对各主分量进行WVD计算,最后将计算结果叠加得到三维时频能量谱,如图8a所示。

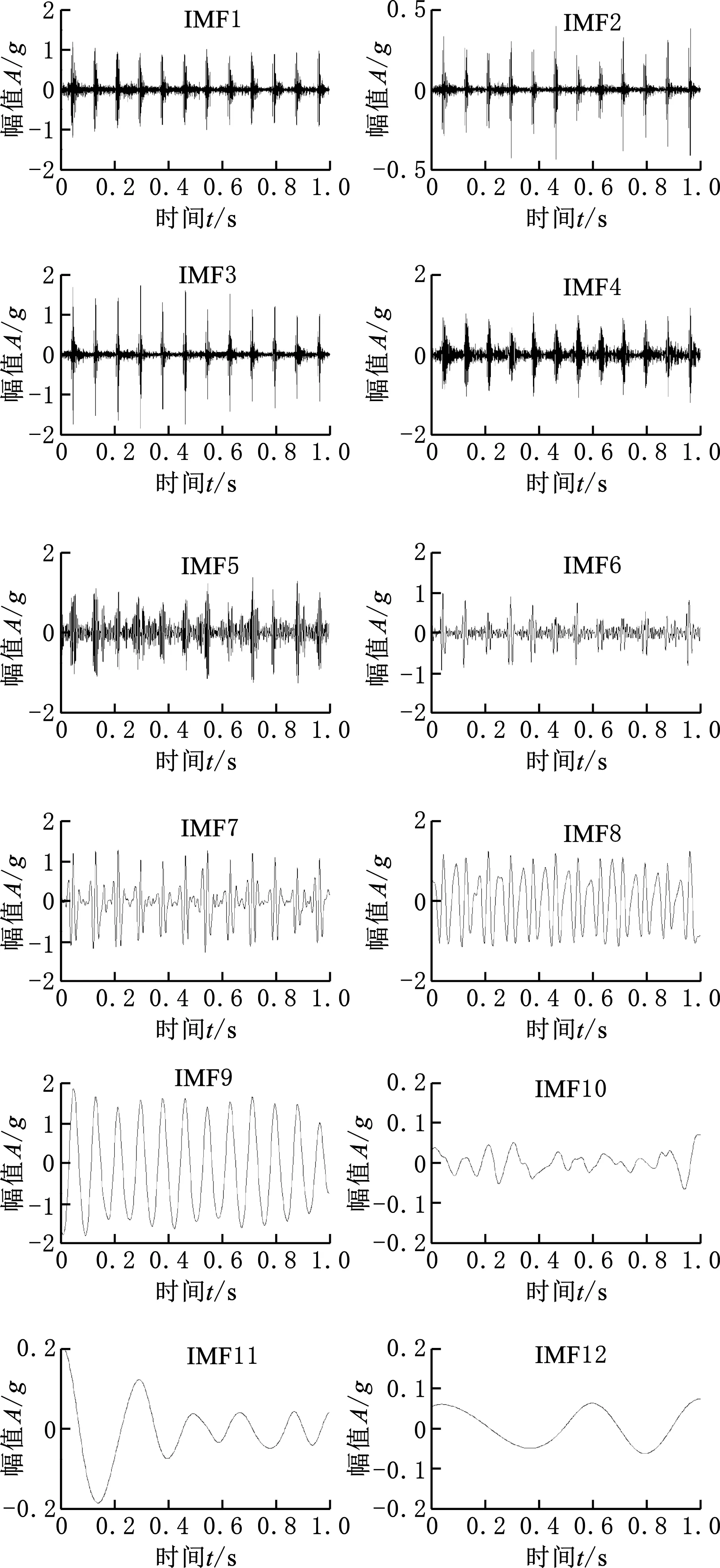
图7 IMF分量时域图

运用前文中建立的车辆轨道刚柔耦合仿真模型,仿真计算车辆在125 km/h和300 km/h两个速度等级下,车轮扁疤长度从20～50 mm的8种工况下,扁疤车轮所在轴箱的垂向振动加速度响应。运用提出的形态学滤波与CEEMDAN-WVD相结合的时频分析方法,处理得到的三维时频能量谱如图8所示。

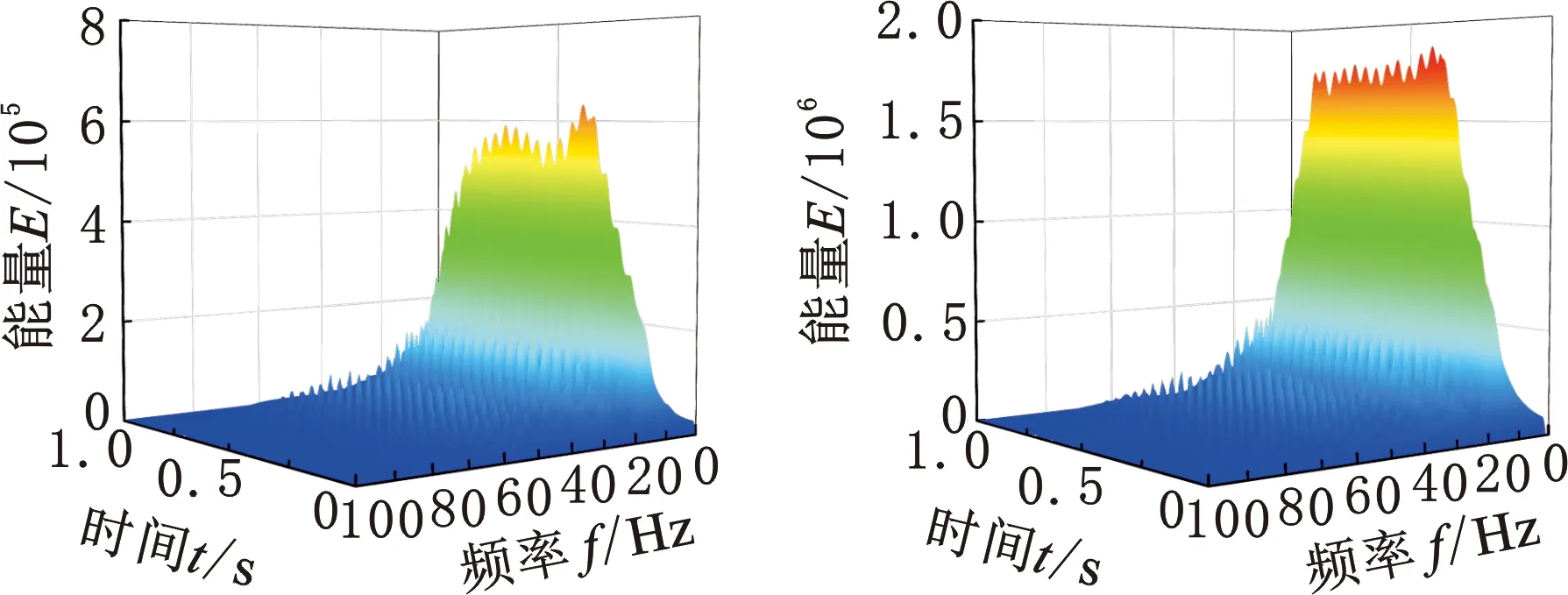
(a)v=125 km/h,l=20 mm (b)v=125 km/h,l=30 mm

(c)v=125 km/h,l=40 mm (d)v=125 km/h,l=50 mm

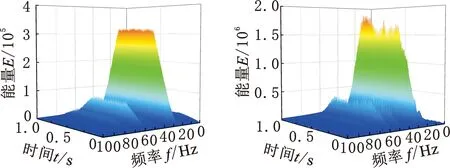
(e)v=300 km/h,l=20 mm (f)v=300 km/h,l=30 mm

(g)v=300 km/h,l=40 mm (h)v=300 km/h,l=50 mm图8 三维时频能量谱

图8a～图8d中都有一条与时间轴平行的频带,其中心频率约为12 Hz,恰好与车速125 km/h时的车轮转频一致。图8e～图8h中也都有一条与时间轴平行的频带,其中心频率约为29 Hz,与车速300 km/h时的车轮转频相吻合。三维时频能量谱中,除与车轮转频一致的特征频带外,还有若干条与时间轴平行且间隔均匀的频带,这是由于车轮扁疤故障的出现,使车辆轴箱振动加速度中包含了车轮转频f和高次谐波2f、3f、…,及分数谐波f/2等成分,因此可依据三维时频能量谱的该特征来诊断车轮是否存在扁疤故障。由图8a～图8h可知,不同长度的扁疤故障在同一车速下引起的轴箱振动加速度在时频能量谱中特征频带一致,但各频带的能量不同;同一长度的扁疤在不同车速下引起的轴箱振动加速度在时频能量谱中特征频带及特征频带的能量值都有差异。通过仿真分析不同车速及不同扁疤损伤程度下的轴箱振动加速度可知:同一车速下,时频能量谱中的峰值随着扁疤损伤程度的增大而增大;同一扁疤故障下,时频能量谱中的峰值随着车速的增大而先增大后减小,因此通过车辆轴箱振动加速度在时频能量谱中的频带分布特征及各特征频带的能量值可以定量地估计车轮扁疤故障的损伤程度。这一规律与许多研究成果一致,也从一定程度上验证了本文所建立动力学模型的合理性。

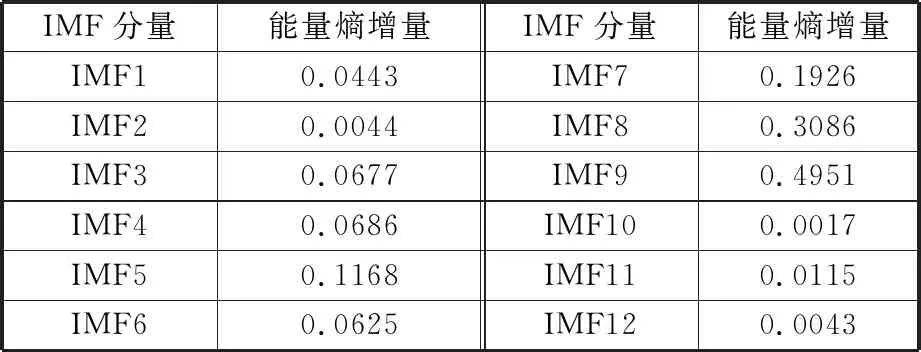
表1 IMF分量的能量熵增量

4 基于VGG16的车轮扁疤损伤程度估计模型

4.1 VGG16网络模型

VGGNet是在AlexNet的基础上发展的深度卷积神经网络[17]。VGG16是VGGNet中经典的卷积神经网络模型之一,由13个卷积层、5个池化层和3个全连接层构成,其中卷积核的大小都为3×3,池化层的大小都为2×2。VGG16因卷积核较小、参数少、非线性拟合能力强等优点而被广泛运用。黄晋等[18]运用VGG16神经网络模型预测了机场能见度。夏坚等[19]提出了基于VGG16深度神经网络的建筑物裂缝检测方法。VGG16在图像识别领域内深受青睐,且都取得了较好的成果,鉴于此,本文运用VGG16模型对轴箱振动加速度时频能量谱进行识别以实现对车轮扁疤损伤程度的定量估计。本文采用的卷积神经网络模型为经典的VGG16模型,结构如图9所示。输入为224×224的彩色二维时频能量谱,输出为车轮扁疤损伤的长度。

图9 VGG16模型结构

4.2 车轮扁疤损伤程度估计流程

基于VGG16的车轮扁疤故障损伤程度估计流程如图10所示。

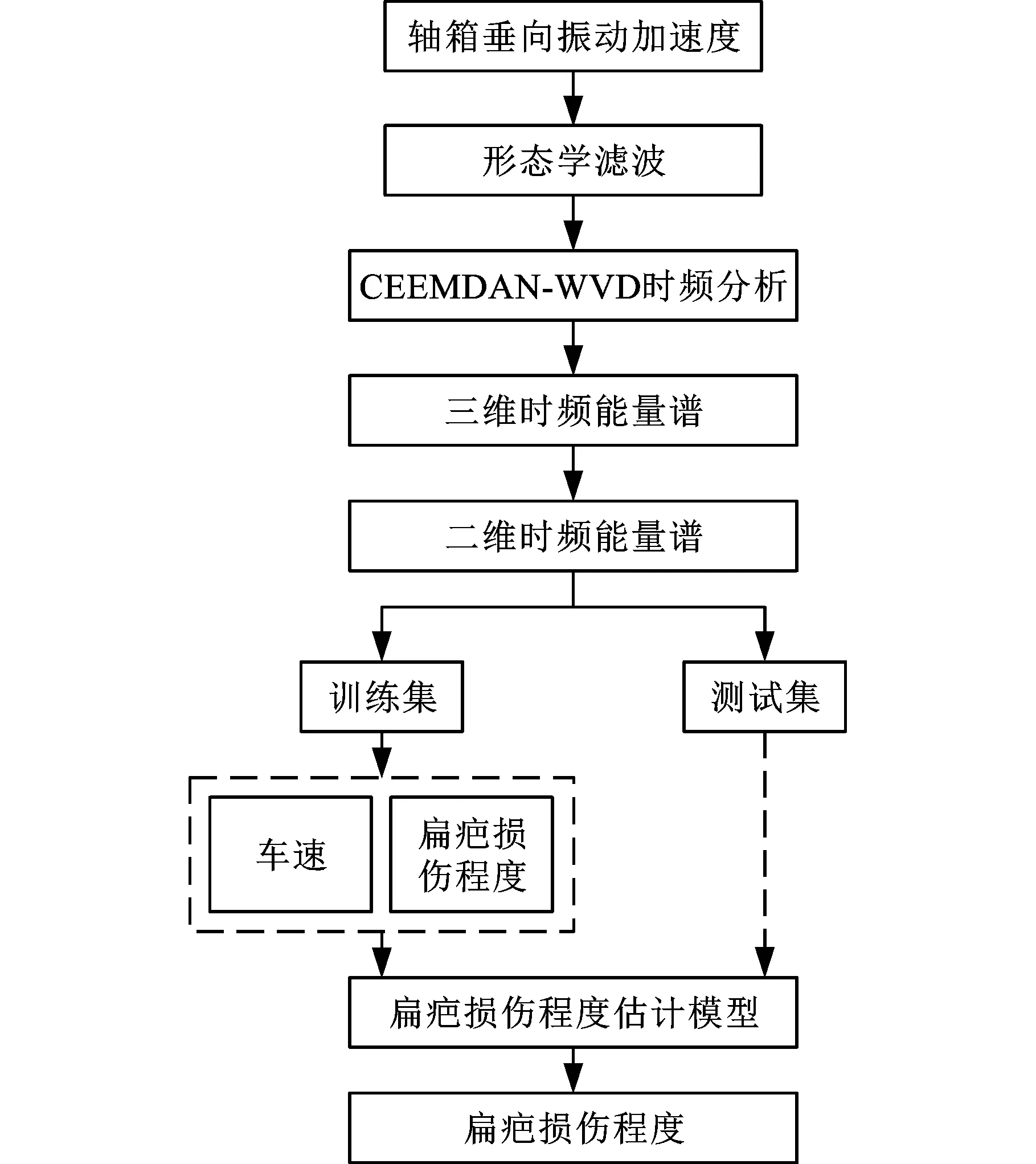
图10 扁疤损伤程度估计流程图

(1)数据获取。运用前文建立的车辆轨道刚柔耦合动力学模型,仿真计算车速50～450 km/h(速度间隔为10 km/h)、车轮扁疤长度10～100 mm组成的410种工况下车轮扁疤引起所在轴箱的垂向振动加速度响应。采样频率为5 kHz,每种工况仿真计算10 s,在仿真结果中随机截取5段长度为1 s的加速度响应。

(2)数据预处理。运用所提出的形态学滤波与CEEMDAN-WVD相结合的时频分析方法,对每种工况下的5段振动加速度响应分别进行时频分析,得到不同工况下的三维时频能量谱。将三维时频能量谱投影到时间、频率所在平面内,并压缩为224×224的二维时频能量谱。以车速200 km/h、车轮扁疤长度90 mm和车速300 km/h、车轮扁疤长度50 mm两种工况为例,经处理后的二维时频能量谱如图11a、图11b所示。

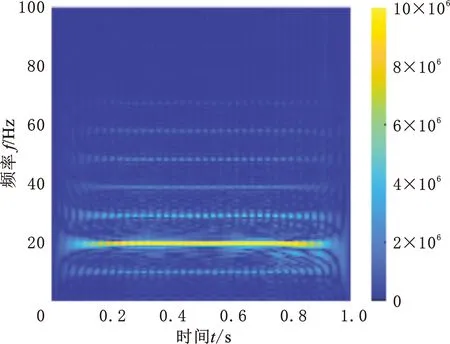
(a)v=200 km/h,l=90 mm

(b)v=300 km/h,l=50 mm图11 处理后的二维时频能量谱

(3)训练集的建立。对每张二维时频能量谱进行双标签化处理(标签包括车速、扁疤长度),构成训练集,共2050张时频能量谱。

(4)VGG16模型的训练。用训练集对前文中建立的VGG16模型进行训练,VGG16模型自动提取、学习时频能量谱中的特征并与其标签建立联系。

(5)模型验证。运用前文中建立的车轨耦合系统动力学模型,随机仿真若干扁疤工况下的车辆轴箱振动加速度响应,经时频分析处理后,将时频能量谱输入到训练完善的VGG16模型中以验证模型的有效性。

4.3 试验验证

为验证本文车轮扁疤故障损伤程度估计方法的有效性,运用前文中所建立的车辆轨道耦合模型,随机仿真计算10种车轮扁疤故障工况下扁疤车轮所在轴箱的垂向振动加速度。首先运用形态学滤波与CEEMDAN-WVD相结合的时频分析方法对不同工况下的加速度信号进行处理得到时频能量谱;然后将时频能量谱处理后输入到训练完善的VGG16模型中,对车轮扁疤故障损伤程度进行估计。仿真工况参数及运用VGG16模型估计的结果如表2所示,轨道谱激扰为武广谱。由表2可见,基于VGG16卷积神经网络的车轮扁疤损伤程度估计方法可以准确地估计出车轮扁疤长度,误差小于1.6 mm,且对车速和扁疤长度都有较好的适应能力。