液冷冷板并联流道流量被动分配研究

2023-09-05方天宇蒋尔进

舰船电子对抗 2023年4期

方天宇,谢飞,蒋尔进

(中国电子科技集团公司第二十研究所,陕西西安 710000)

0 引言

随着现代电子技术的飞速发展,军用相控阵雷达对热设计的要求表现出了2个显著的特征:过高的热流密度使得风冷在相控阵雷达中的应用减少,液冷技术正得到来越广泛的应用;均温性的要求使得流道的结构形式逐步由集中式向分布式过渡,由此带来的并联管路的流量分配正成为液冷系统研制的一个重要问题[1-2]。目前,介绍相控阵雷达液冷技术的文献较多,但是对液冷系统中单个冷板内部流量分配技术详细论述的文献较少。本文结合某相控阵雷达液冷系统的研制对单个冷板中并联流道的流量分配问题进行了重点研究。

1 问题描述

本文拟针对单冷板内并联流道的结构进行设计,使得并联流道内的流量分布较为均匀。针对图1所示的原始流道结构进行改变,使得并联流道内流量分布较为均衡。针对图1所示的流道进行仿真,得到的流道中流速分布如图2所示。

图1 流道原始结构

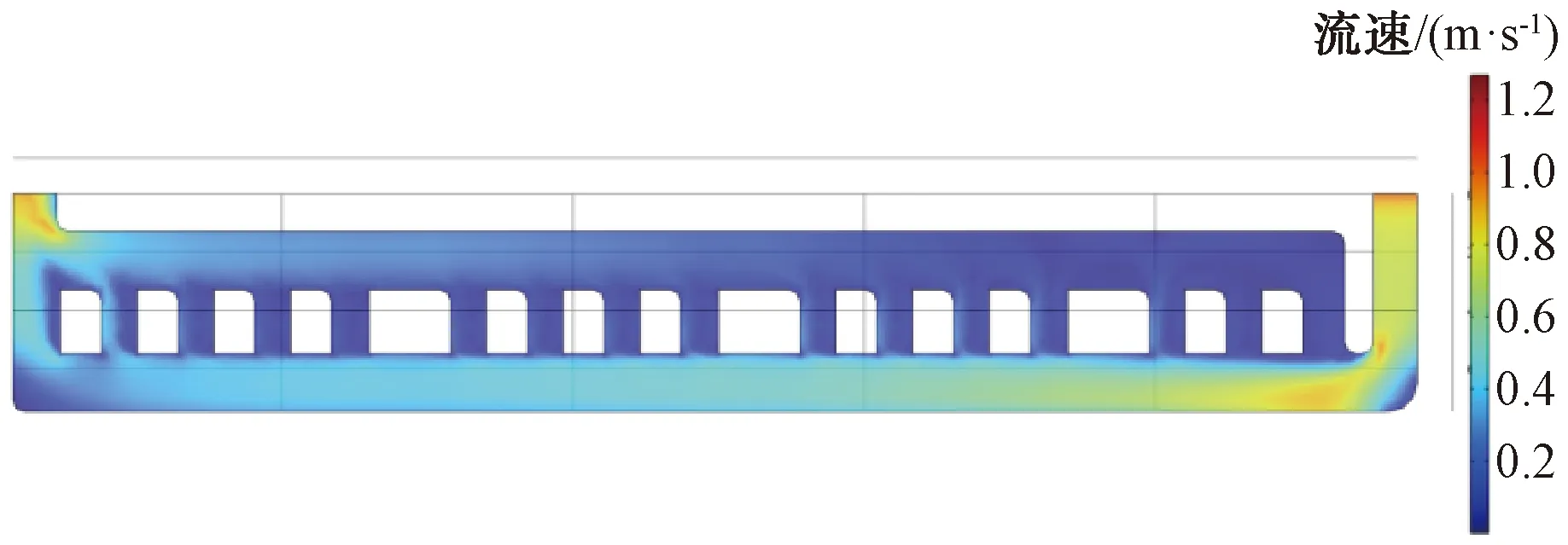
图2 原始流道结构的流速分布

可以看出:并联流道中的流量分布极其不均匀,故此需要对流道的结构进行调整,使得并联流道内的流量分布较为均匀。

2 流道最优结构设计

2.1 流道可变结构设计

为了改变并联流道内的流量分配,在分路的来流方向处增加三角形的导流块,将三角形迎向来流一边的长度记为Hi(i=1～15),见图3。将15个Hi组成的向量称之为流道变化向量,记为H。增加导流块后的流道见图4。针对每个分路导流块的Hi进行改变来调节对应分路内的流量[3-5]。

图3 Hi示意图

图4 增加导流块后的流道

图5 流道结构寻优算法流程图

对于不同的流道变化向量H都有不同的流量分布,下面论述如何寻找流量分布最优对应的流道变化向量H。

2.2 寻优算法

本文研究的问题可以归纳为下列组合优化问题:

find:{h1,h2,…,hM}∈{hi,|i=1,2,…,15}

(1) 给定流道变化向量H初始向量,进行流道仿真,获取各个分路的流量Qi,将15路分路流量Qi组成的向量称为流量向量,记为Q;

(2) 将入口流量的1/15设为目标数值,记为M,将M、Q代入ΔH=F(Q,M)中,计算得到流道修正向量ΔH;

(3) 将流道修正向量ΔH代入H=H+ΔH中,求得流道变化向量H;

(4) 将Hi代入仿真中进行计算,获取各个分路的流量Q;

(5) 计算Q的均方差进行判断,是否继续循环,是的话重复(2)～(4),否的话进行(6);

(6) 将结果输出。

各个变量定义:

流道变化向量:H={H1,H2…H15}

流量分路向量:Q={Q1,Q2…Q16}

流道结构修正向量:ΔH={ΔH1,ΔH2… ΔH15}

流道修正函数:ΔH=F(Q,M)

Matlab主要控制函数:

While((N<100) &&(var(X)>0.02)) %停止条件model.component('comp1').geom('geom1').run;%更新模型

model.study("std1").run();%求解

model.result().evaluationGroup("eg1").run();%求解计算组,并输出X至TXT

X=(dlmread('LiuLiang.txt',' ',5,0))';%偏移5行0列读取数据

X(all(X== 0,2),:) =[];%删除向量中的零元素。

X=-X;

M=mean(X);%取均值。

fori=1:16

DASDA=(abs(X(i)-M));

DASDA2=(0.05×M);

DASDA>DASDA2;

if(DASDA>DASDA2)%超过0.05×M进行结构变化,否则按照上次结构继续。

Y(i)=F(X(i),M);%计算Y

end

if(Y(i)>=20)

Y(i)=19.9; %超过20的话回归。

end

DX(N,:)=X' %保存X结果

DY(N,:)=Y' %保存Y结果

model.param.set('H1',Y(1)); %将Y赋予模型

model.param.set('H2',Y(2));

model.param.set('H3',Y(3));

model.param.set('H4',Y(4));

model.param.set('H5',Y(5));

model.param.set('H6',Y(6));

model.param.set('H7',Y(7));

model.param.set('H8',Y(8));

model.param.set('H9',Y(9));

model.param.set('H10',Y(10));

model.param.set('H11',Y(11));

model.param.set('H12',Y(12));

model.param.set('H13',Y(13));

model.param.set('H14',Y(14));

model.param.set('H15',Y(15));

N=N+1;

end

3 流道仿真

3.1 流道仿真边界条件

(1) 环境温度35 ℃;

(2) 入口处冷却液温度为35 ℃;

(3) 冷却液类型为去离子水。

3.2 流道仿真模型

流道仿真分析计算采用分析软件COMSOL进行,根据软件建模的特点和要求,在保证仿真结果不失真的前提下,对仿真模型进行了部分简化,忽略了所有螺钉孔以及与冷板流动关系不大的局部特征。将流道在仿真模型中分为两部分,为获取流量分路向量Q做准备。给定流道变化向量初始值H=5。流道仿真分析模型如图6所示。

图6 流道仿真分析模型

运行编制好的程序后,得到了优化后的流道变化向量:H=[6.019 5,5.958 8,6.160 8,5.269 4,5.885 6,6.534 7,7.802 9,7.874 5,9.667 6,11.145 8,13.022 6,13.847 3,15.566 7,16.983 8,17.976 5,13.134 3]。

根据H进行建模得到图7所示冷板,对其进行流量仿真,结果如图8所示。

图7 优化后的流道仿真分析模型

图8 优化后的流道仿真分析结果

根据对流道截面上的速度在z方向的分量进行积分得到流量分路向量:Q=[ 0.285 3,0.274 5,0.284 8,0.292 5,0.272 6,0.285 0,0.282 3,0.279 9,0.272 3,0.277 9,0.285 5,0.294 0,0.277 6,0.272 3,0.285 5,0.284 6] ·10-5m3。

可以看出Q的各个分量均在M的±5%以内,满足10%精度的要求,认为本次优化的结果可用。