风冷散热翅片阻力及传热特性的参数化数值研究

2023-09-05张方驹范鹏杰

舰船电子对抗 2023年4期

张方驹,刘禹,范鹏杰,方堃,常伟

(中国船舶集团有限公司第七二三研究所,江苏扬州 225101)

0 引言

随着半导体技术的发展,机载电子设备不断趋于体积微型化和功能多样化,但随之而来的是电子器件热流密度过大、局部温度过高等一系列问题。据统计,55%的电子器件失效原因是温度超出了规定阀值[1],且随着温度的升高,电子器件的失效率呈指数增长[2]。因此,热设计是电子设备设计中非常重要的环节。机载设备通常对体积、重量要求严格,因此大多采用风冷的散热方式,以充分利用高空的低温空气。

风冷散热通常利用肋壁(翅片)来增加散热面积,以强化换热。英国马尔斯顿·艾克谢尔瑟公司1930年就在板式换热器的基础上增加翅片,用作航空发动机的散热器[3];张笑凡等进行了机载大长宽比风冷均温板翅片的优化设计[4];郭建忠等通过仿真研究了变角度翅片结构对散热性能的影响分析[5];施兴兴等研究了翅片间距对传热与阻力特性影响的试验研究[6];Wang等通过大量试验研究了不同翅片结构参数对换热与阻力特性的影响[7-9]。本文基于某小型机载雷达热设计与热仿真,对风冷散热翅片的齿形、齿距、齿厚等不同结构参数对散热效果的影响进行研究与分析,为此类热设计提供参考和依据。

1 模型的建立

1.1 物理模型

某小型机载雷达发射/接收(T/R)组件设计简化结构如图1所示。外形尺寸为210 mm×92 mm×9.5 mm,热源发热量为168 W,热流密度达60 W/cm2。热源两边为翅片,增加散热面积,底板厚3.5 mm,做成均热板以增强二维热扩散能力。T/R组件共16组,依次排列,通过散热翅片形成风道。

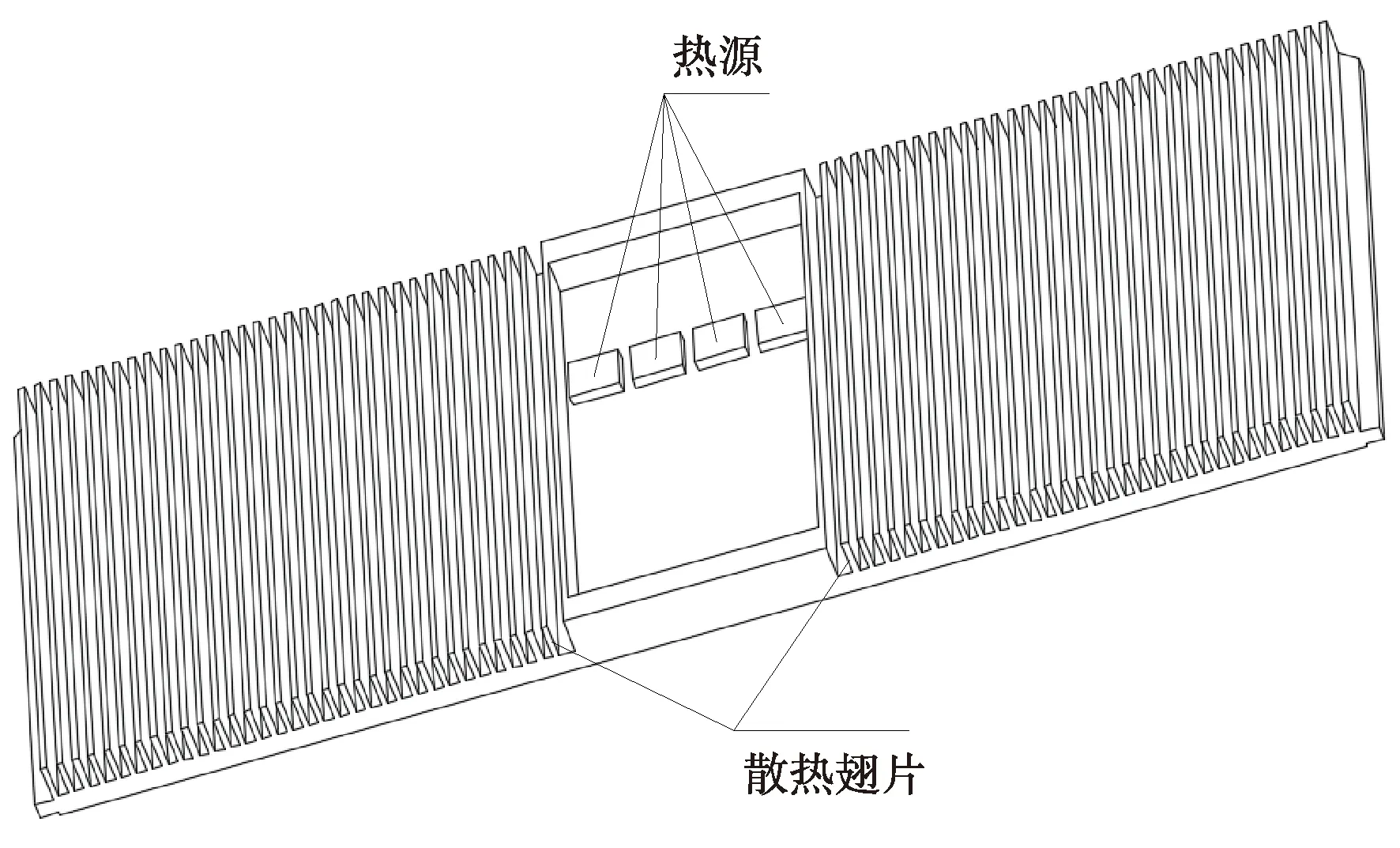
图1 T/R组件结构简图

对于给定高度的散热翅片,定义翅片几何参数如图2所示。图中t为齿厚,s为齿距,d为打断,其它参数齿高为6 mm。

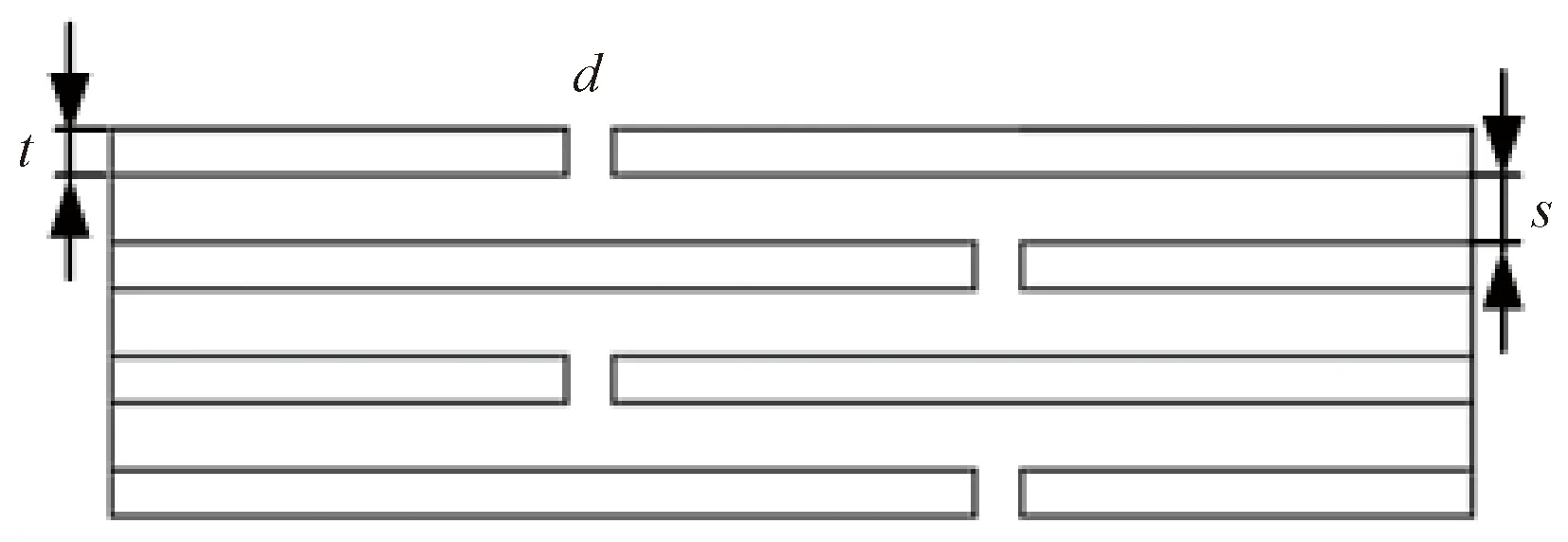
图2 翅片几何参数

为研究齿形、齿距、齿厚的不同对热源散热的影响,根据实际情况确定研究的变化因子与变化水平,如表1所示。

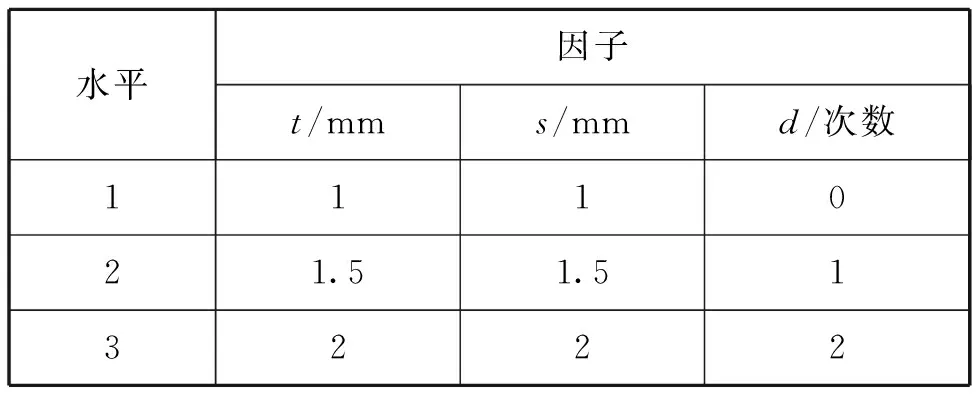
表1 变化因子水平表

根据正交设计表[10]L934,并结合实际情况对变化因子与变化水平进行安排研究,如表2所示。

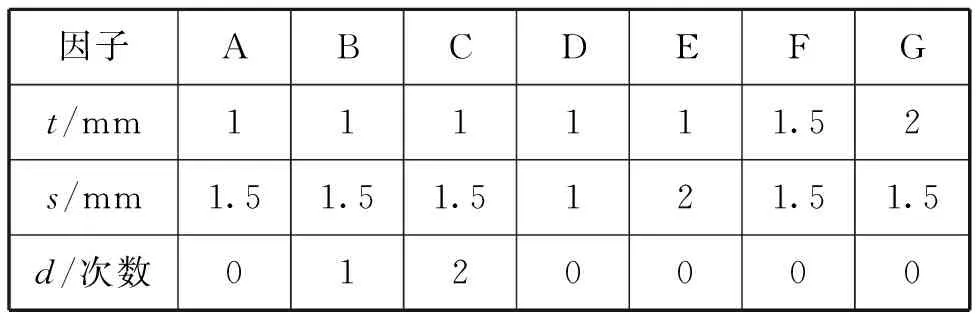
表2 参数研究安排表

工程实际中,风冷散热通常是给定风机型号,因此研究选取某型国产风机来提供冷风,如图3所示。根据调节转速的不同,共有3条风量风压特性曲线。风机外形尺寸为50 mm×50 mm×28 mm,上下2组风机,每组3个,共6个风机。海平面空气温度为15 ℃。

图3 风量风压特性曲线

1.2 数据处理

根据传热学原理,系统换热量:

Q=cairmair(Tout-Tin)=hA(Tw-Tf)

(1)

式中:Q为系统换热量,由热源发热量可知;cair为定性温度下的空气比热;mair为空气质量流量;Tout为空气出口温度;Tin为空气进口温度;h为对流换热系数;A为总换热面积;Tw为壁面温度;Tf为空气温度。

均热板理论导热系数达20 000 W/(m·K),实际导热系数也可达3 000 W/(m·K),底板温差较小,且翅片高度较低,因此假定均热板平均温度为Tw,空气进出口平均温度为Tf。由此可得努塞尔数Nu:

(2)

式中:d为当量直径,d=4Vfree/Awet,Vfree为翅片内空气自由流通的体积,Awet为翅片内空气自由流通的湿润面积;λ为流体导热系数。

代表传热性能的传热因子j计算公式为[11]:

(3)

式中:Pr为普朗特数;Re为雷诺数。

代表阻力性能的摩擦因子f计算公式为[11]:

(4)

式中:d为当量直径;L为翅片长度;Δp为空气压降;ρm为定性温度下空气的密度;w为空气的平均流速。

对于强化换热表面,努塞尔数越大,摩擦因子越小,换热性能越优越。在众多不同的强化换热表面中,应选择一种既能强化换热,又不会引起较大摩擦损失的表面。因此,选择一种判断表面综合性能的标准十分关键。Shah[12]提出强化表面换热品质的评价标准,即热性能因子(TPF),翅片的TPF值越大,综合性能越好:

FTPF=Nu/f1/3

(5)

2 仿真结果分析

2.1 各模型散热效果对比分析

选取3种风机作为工况边界条件,通过仿真计算,得到模型A、B、C、D、E、F、G 7种结构形式翅片对应的热源温度T/℃、风量V/m3·h-1和压降ΔP/Pa,数据整理如表3所示。

表3 3种工况下各模型参数表

热源温度的高低反映了不同结构形式翅片的散热效果,热源温度越高,散热效果越差,图4直观地显示了7种不同形式的翅片所对应的热源温度。

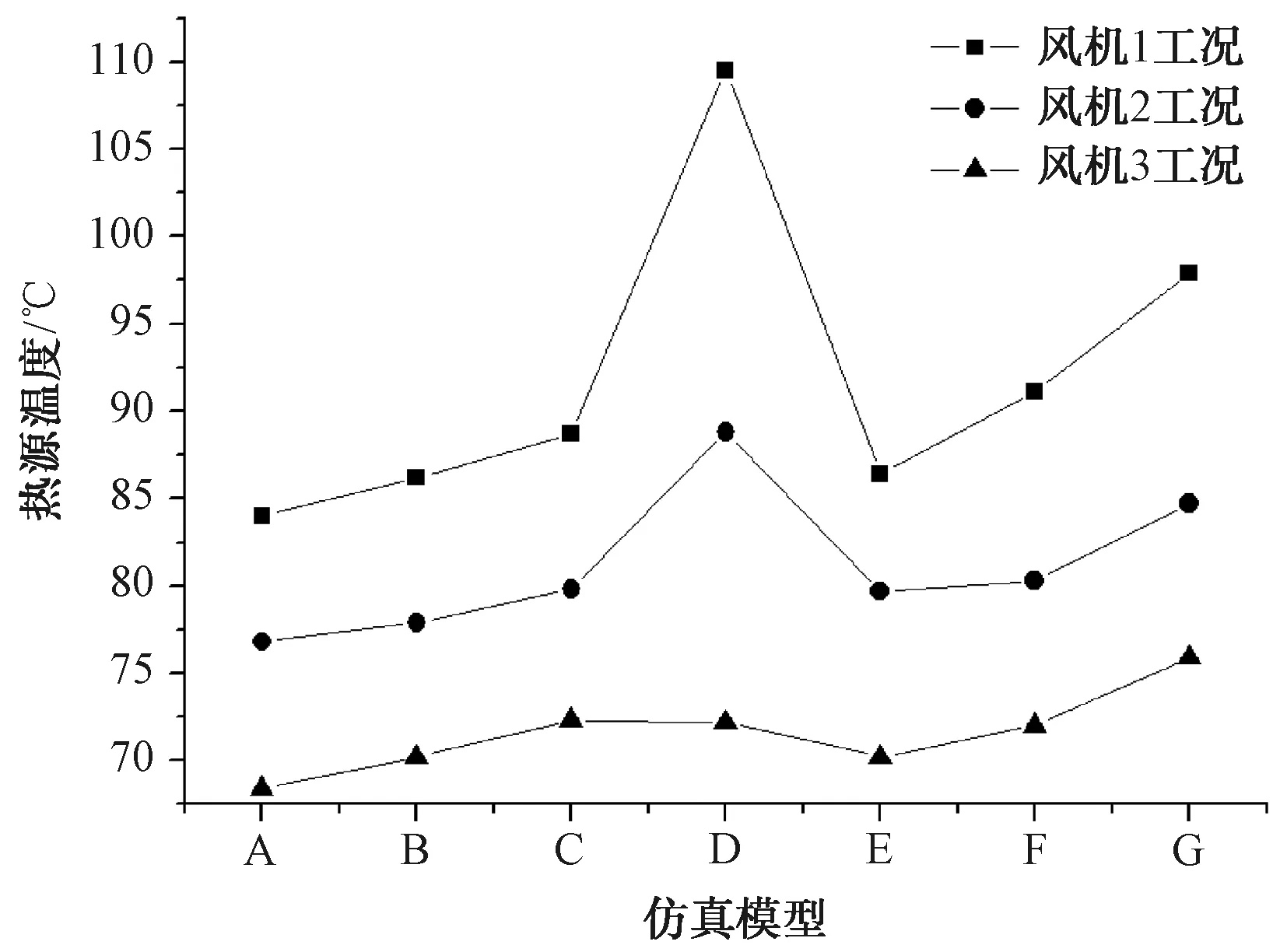
图4 各模型散热效果对比

选用模型A作为对照组,分别与其它6组模型进行对比。比较模型A、模型B、模型C 3组数据可知,齿距、齿厚不变,随着翅片打断的增多,热源温度逐渐升高,原因是翅片的打断虽然增强了空气流动时的紊流,能够增强换热,但是流阻增加,导致风机送风量减少,综合作用下翅片散热效果降低。比较模型A、模型D、模型E 3组数据可知,齿厚、打断不变,当齿距由1.5 mm减小为1 mm时,热源温度升高,齿距的减小虽然增加了二次换热面积,但是有效流通截面积减小,摩擦增大,流阻增加,导致风机送风量减小,综合作用下翅片散热效果降低;当齿距由1.5 mm增大到2 mm时,热源温度升高,齿距的增加虽然加大了有效流通截面积,减小了摩擦,风机送风量增加,但是二次换热面积减小,综合作用下翅片散热效果同样降低,1.5 mm的齿距换热效果最优。比较模型A、模型F、模型G 3组数据可知,齿距、打断不变时,随着齿厚从1 mm增加到2 mm,热源温度逐渐升高,齿厚的增加减小了有效流通截面积,流阻增加,风机送风量减小,且二次换热面积同时减小,因此散热效果降低。值得关注的是,随着风机转速的增加,模型D的散热效果提升很快,原因是随着风机风压和风量的增大,截面积减小导致流阻增加对散热效果的影响越来越小,二次换热面积增加对散热效果的影响越来越大,当风机风量风压足够大时,模型D也能达到较高的散热效果。

由分析可知,在选定风机的工况下,翅片的打断降低了翅片的散热效果,选择无打断的翅片散热效果最优;翅片的疏密对散热效果的影响很大,选择合适的齿距才能达到最佳的散热效果;齿厚的增加不仅增加了流阻,而且减小了二次换热面积,因此选择更薄的翅片能得到更优的散热效果,综合对比下,模型A(齿厚1 mm、齿距1.5 mm、无打断)拥有最佳的散热效果。

2.2 各模型综合性能对比分析

对散热翅片的性能评价,不是散热效果越高越好,也要综合考虑散热翅片对强化换热的增强作用,以及对来流气体的阻碍作用,因此选用综合性能评价因子TPF对各模型进行评价。图5给出了各模型传热因子、阻力因子、TPF随雷诺数的变化趋势。从图5(a)中可以看出,随着雷诺数变大,各模型传热因子均减小,强化换热效果逐渐降低;从图5(b)中可以看出,随着雷诺数变大,各模型阻力因子均减小,阻力性能逐渐提升;从图5(c)中可以看出,随着雷诺数变大,各模型综合性能评价因子TPF均减小,综合性能逐渐降低。

同雷诺数下,模型A、模型B、模型C的传热因子与阻力因子逐渐增加,原因是翅片的打断增加了空气湍流,增强了换热效果,同时也增加了流动阻力,三者中模型A拥有最佳的综合性能;同雷诺数下,模型D、模型A、模型E的传热因子与阻力因子逐渐增加,原因是大齿距对应更大的当量直径,空气流速较低,低流速时换热更加充分,同时流动边界层更厚,流动损失更大,三者中模型E拥有最佳的综合性能;同雷诺数下,模型A、模型F、模型G拥有相同的流速和齿形,因此传热因子、阻力因子、综合性能均相同。综合对比7种模型,模型E拥有最高的传热因子,即最佳的换热性能,模型D拥有最低的阻力因子,即最佳的阻力性能,模型E拥有最高的TPF,即最优的综合性能,对于不同的传热及压降设计要求,可以选择不同的散热翅片。