基于空间格的连续时间空域特征提取算法

赵小瑞,李宏权,梁复台,3,杨 凡

(1.空军预警学院,湖北 武汉 430019;2.解放军96714部队,福建 永安 366000;3.解放军31121部队,江苏 南京 210000)

0 引 言

预警探测体系中,目标航迹数据具有量大、更新快、价值高等特点。如何高效利用目标历史航迹大数据,从数据中挖掘其蕴含的价值,寻找目标内在的规律,为快速、准确地判断空中目标提供支撑是当前研究的热点。在数据压缩上,文献[1]提出基于空间曲线压缩算法的空中目标航迹提取算法,通过设定阈值提取关键点的方法,减少数据量,降低了计算的复杂度。航迹匹配通常采取K-means算法、层次方法[2]等进行航迹拟合聚类,再建立神经网络预测模型[3]进行航迹匹配。文献[4]提出一种多属性加权关联关系匹配模型,重点解决热点区域战略空中目标经典航迹提取及实时航迹的关联匹配问题。目前大部分文献都是针对数据本身进行筛选,航迹匹配只与当前输入的数据有关,对历史数据利用率不高,对应结果只能反映当前数据信息,不具备可持续性。

本文针对空中目标航迹数据量大、运算量过高,传统目标航迹空域特征提取较为复杂的情况,提出基于空间格的连续时间空域特征提取算法。通过对选定空域以一定长度为单位距离进行网格化划分,再将收集到的航迹大数据进行预筛选、坐标转换,将航迹点与网格对应匹配,统计出每个网格内出现的航迹点次数,实现对目标航迹空域特征的提取,保留能突出航迹特点的网格,以减少数据量。并且可随着数据的不断输入,结果不断更新,该结果可反映出输入数据所有时间的航迹总体规律,避免了历史数据利用率不高以及结果反映过于片面的问题。

1 相关概念

(1) 空间格定义

(2) 空间格坐标

空间格采用直角坐标系,将指定区域地图的左下角坐标作为空间格的原点(0,0),以正东方向为直角坐标的x轴,正北方向为直角坐标的y轴,以a作为单位长度,将空域范围划分成m×n的二维网格,每个网格都有一个唯一的编号,即由空间格左下角的x轴和y轴坐标组成,坐标之间用逗号分隔。

(3) 目标空域特征

目标空域是指目标所在的空间位置。对于空中目标而言,目标空域通常由目标情报点的经度、纬度和高度来表示。单批目标的空域信息就是由其整条航迹所有点的经度、纬度和高度构成;某类目标的空域信息就是由该类所有历史航迹数据点的经度、纬度和高度构成。目标空域特征是指能够表征某批或某类目标空间位置信息的典型、有代表性的特殊数据集。本文所研究的目标空域特征就是以空间格为基础,将历史航迹的空间位置信息映射到空间格之中,进而获取某批或某类目标的空域特征值。

(4) 目标空域特征提取

特征提取就是在目标空域网格化的基础上,将目标航迹数据点按照地理坐标位置,对应放入网格中,同时对前后小于30 s的2个点进行连接,将2点间航迹粗略看成直线[5],航迹点本身,以及按时间顺序相连的直线所经过的网格,其对应点数全部加1,以便增加对航迹判别有帮助的点数量。

2 基于空间格的特征格提取

由于常用算法大部分对单条航迹进行特征点提取,不具有针对时间的连续性。因此本文提出基于空间格的连续时间空域特征提取算法进行目标空域特征提取。首先需要对原始航迹进行预处理,筛选出符合要求航迹点的基础上,对目标活动空域进行网格布设,其次通过航迹坐标变换,实现航迹点空域映射,最后得到目标空域特征矩阵。

2.1 空域格构建

对目标活动空域进行网格化处理,将目标空域映射到直角坐标系中。首先需要确定空域的区域范围,然后根据区域边缘经纬度信息,按照经纬度距离公式,求出最大区域距离范围,再根据设定的网格边长,求出划分网格的长宽个数m×n。

需要特别注意的是数据空域范围的选定,由于网格是由多个方格构成的矩形,受地球曲率影响,相同距离下,在低纬度地区跨过的经度要比高纬度地区跨过的经度少。地球上同一经度上所有纬度1°间的距离均约为111.12 km,即1′的距离均约为1.86 km,而对于同一纬度,2个不同经度的距离为:

d=111.12(x2-x1)cosy

(1)

式中:d为同一纬度y上2点之间的距离,单位为km;x1、x2分别为2点经度,单位为°;y为纬度数据,单位rad。

由于2个经度之间,高纬度长度低于低纬度,为了空间格的完整度,需要将高纬度的长度延长至低纬度长度,故高纬度区域的截止经度将会发生改变。高纬度调整后的经度计算方法为:

(2)

2.2 空间格数据处理

目标航迹数据包含经度、纬度、时间、类型、批次、架数等信息。将航迹点对应到相应空间格中,则需要对数据进行坐标转换,航迹坐标变换就是将目标航迹点的经度和纬度从地理坐标转换成空域网格坐标。设航迹点数据集合为Hi={P1,P2,…,Pk,…,Pn},其中n为航迹点总个数,Pk=(类型,架数,ak,bk),ak为第k个航迹点坐标经度,bk为第k个航迹点坐标纬度(1≤k≤n)。

以选定空域高纬度为x轴,以西侧经度为y轴,两者交点为原点,建立笛卡尔坐标系。将航迹点数据集合Hi={P1,P2,…,Pk,…,Pn},即Pk=(类型,架数,ak,bk)的经纬度坐标,转换为空域网格坐标系里的距离坐标,即pk=(类型,架数,xk,yk)。其中xk的坐标为:

xk=111.12(ak-109°)cosbk

(3)

同理,yk的坐标为:

yk=111.12|bk-21°|

(4)

形成一个新的数据点集合Hi={p1,p2,…,pk,…,pn},pk=(类型,架数,xk,yk),xk为第k个数据点横坐标距离位置信息,yk为第k个数据点距离位置信息。

2.3 空间格生成步骤

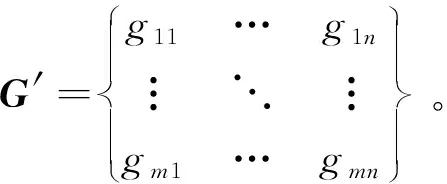
基于空间格定义,构建空间格数据存储矩阵,然后将航迹点空间特征值存入空间格矩阵。令空间格矩阵为G=(gij)m×n,gij=(类型,架数,次数),i、j分别为空间格第i行、第j列的网格坐标,0≤i≤m,0≤j≤n。具体步骤如下:

(3) 判断若i1≠i0,且|k|≥1,则将j0与j1之间的整数值依次代入函数关系式中的值y(j),求出对应的值x(i),并将x(i)向上取整,对应的gij中对应的次数加1。若|k|<1,则将i0与i1之间的整数值依次代入函数关系式中的值x(i),求出对应的值y(j),并向上取整y(j),对应的gij中对应的次数加1。

(4) 读取新的航迹数据,再次执行(1)～(3)。

2.4 特征格提取步骤

将点数较高的网格予以保留,但是防止航线过于密集,而出现整体航迹占用网格较宽的情况,只保留最密集最能体现航迹规律的网格;同时,对于数量不多,但是和其他航迹有明显区别的航迹,所占用的网格也要保留。步骤如下:

(1) 以单个单元格中的数据点出现的次数为横轴,以包含同一数据点量的单元格数量为纵轴,画出柱状图;

(2) 设定单个单元格点内数量阈值为M,若不少于M,则单元格暂时保留,并采用3×3的框架,将框架中的数据数量Aij进行排序,取最高的3个值的单元格予以彻底保留,舍弃其他的单元格;

(3) 若阈值小于M,但频次不少于给定阈值N,则单元格暂时保留,且以此单元格为中心,用3×3的框架,框架内,若暂时保留的单元格数超过3个,则将所有暂时保留网格予以彻底保留,否则将该单元格去除;

3 仿真实验分析

以南北纵跨为400 km、纬度横越为180 km的某空域为例。由于大多预警雷达扫描1圈的时间约为10 s,目标飞行速度通常为800 km/h,则10 s内的飞行距离约为2.22 km,故将空间单元格的边长设为2 km,空间格由200×90个单元格组成。数据来源为某站1周内在该区域经过数据预处理后的150条航线的8 959条雷达数据。

将数据进行初步清洗后,按本文方法进行坐标转换,而后对应到空间格中,数据点数量即空间格矩阵数值分布如图1所示,横坐标为矩阵元素数值,纵坐标为单元格数量,其中不包括数据量为0的单元格数量。

图1 空间格矩阵数值分布图

空间格矩阵做成的热力图如图2所示。

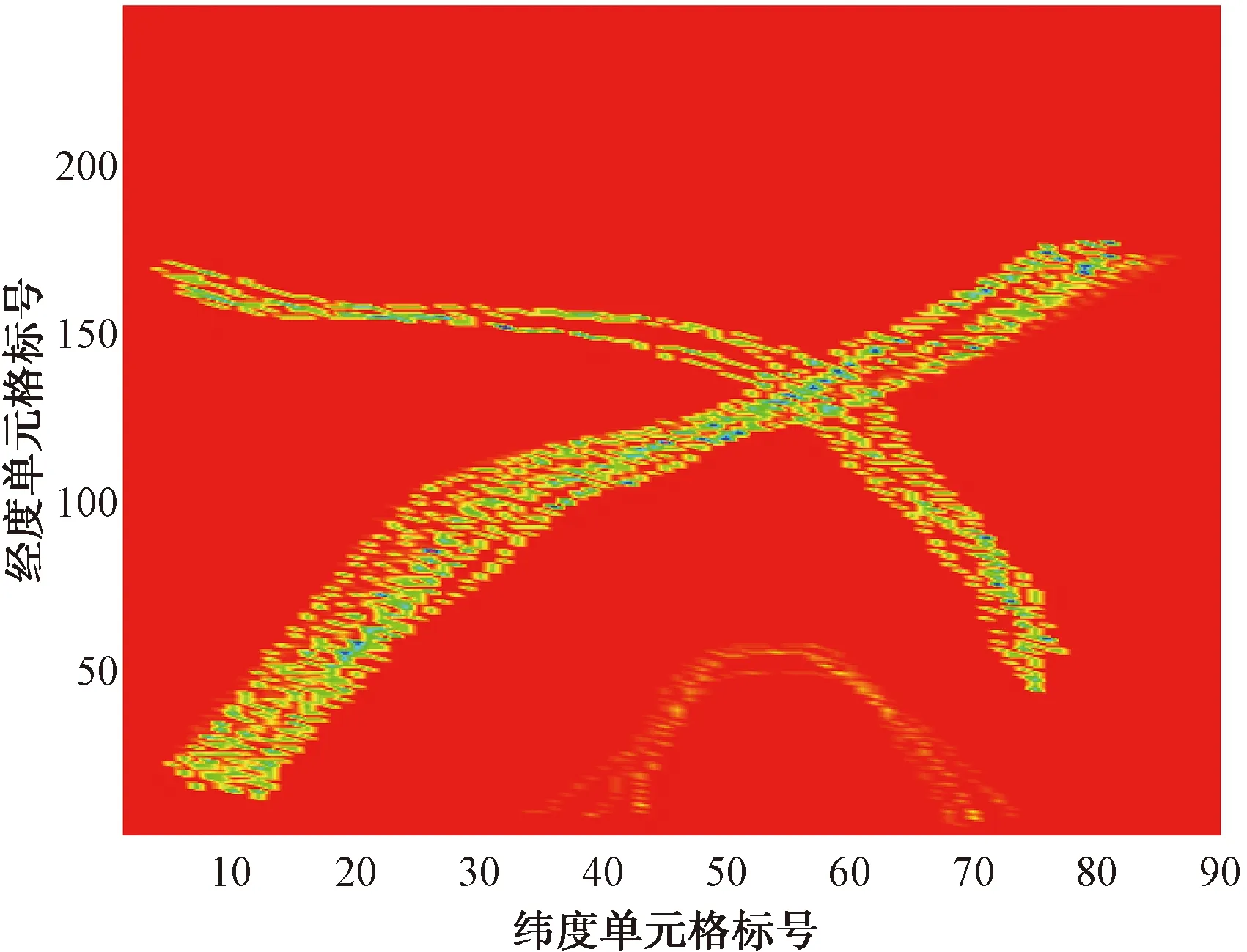
图2 空间格矩阵热力图

由图1可知,横坐标中位数为12,因此将M阈值设为12,可得结果如图3所示。筛选出典型航迹,但是原数据中下方的少量异常航迹被消除,损失了重要信息。从图1也可以直观地看出,众数为6,即有700多个单元格中包含的数据点数量为6,因此可以得出结论:虽然数据点数量较少,但同时有大量单元格拥有相同数据,证明此处很可能包含数据量较少的异常航迹,因此将2.4步骤中的阈值N设为5而不设置成6的原因是尽量保证异常航迹的数据量。得到的特征格矩阵做成热力图如图4所示,异常航线显现。

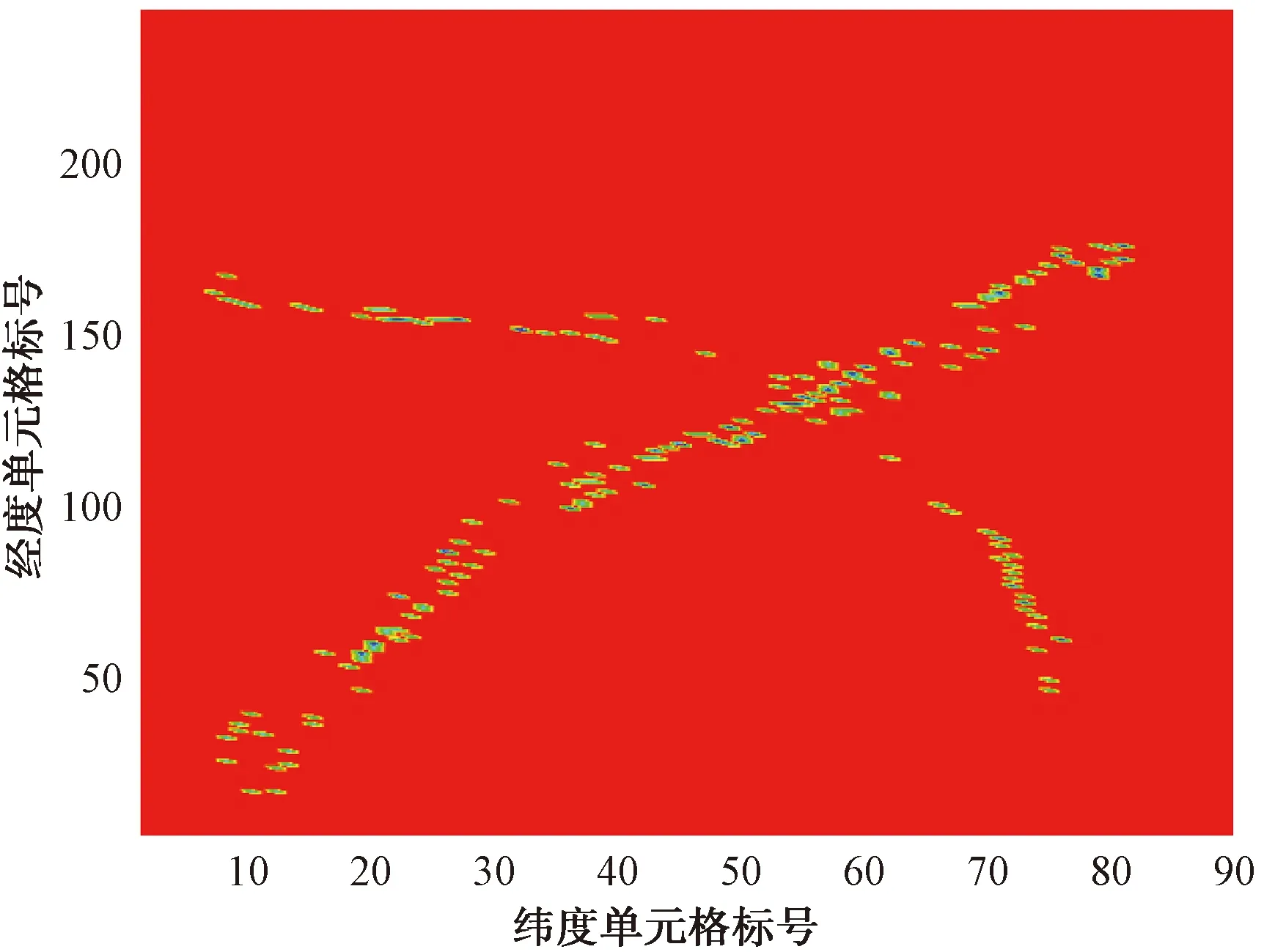
图3 筛选后的高频航线热力图

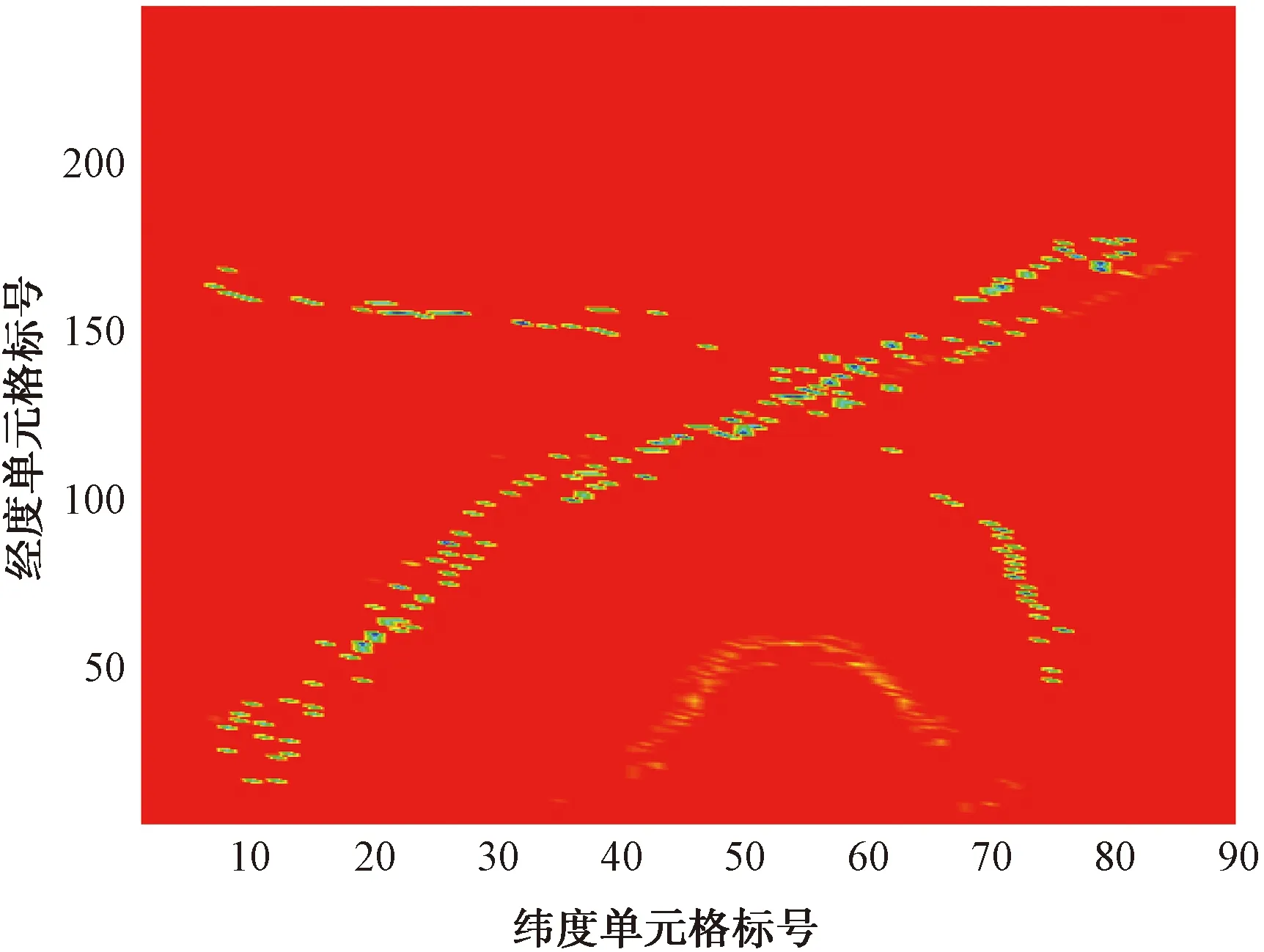
图4 特征格矩阵热力图

由图4可以直观看出,未经处理的航线数据较多且密集,经过特征网格提取后的航线,数据量少很多,并且很好地保留了原有航线的特征,下方数量较少的异常航线也被很好保留。原8 959条数据,经过生成空间格,数据量减少至1 671,经过提取特征格后,数据降为341,仅为原始数据的3.81%。

本算法的优势在于:存储空间最多为m×n×2(空间格矩阵及特征格矩阵大小),此后不会因为原始航迹的增加而增加。航迹关键点提取[1]和曲线拟合法[6]等传统航迹处理方法,都是对航迹点进行压缩,达到用最少的参量来表示整条航迹的运动特征。但算法的处理能力有限,可同时处理的航线最多为几十条,并且着眼于数据本身,反映的结果是当前输入的数据。本文方法可随着数据的不断输入,特征网格位置随着输入数据的增加而发生变化,聚类结果能反映出随着时间推移的总体航迹趋势。因为航迹点的增加最终都会对应成空间格矩阵中的数值变化,理论上可处理的数据无上限,但是若处理的数据在时间跨度上过长,会导致大量历史因素对结果产生影响,降低时效性。

4 结束语

本文基于空中目标的历史大数据,提出对目标空域进行网格化处理,生成目标活动空间格。基于布设的空间格,将历史航迹的空间位置映射到空间格中,实现目标空域特征的提取,也就是将海量的历史航迹数据转变成有限的空间格数据集。经过算法处理后,大幅减少了数据量,在存储空间利用、对连续时间的轨迹研究等方面具有较为明显的优势,便于后续对目标的空间活动规律进行聚类、分类、关联关系等分析。并且本算法具备可持续性,可不断输入新数据进行规划完善,输入数据越多,航迹聚类越精确,且不增加数据存储容量。但是此方法忽略了目标航迹高度的影响,下一步还需把高度纳入考虑范围,对空间格进行三维化处理。