纵向肋条对斜拉索气动力和涡激振动特性影响的试验研究

2023-09-05孙一飞邵林媛刘庆宽

振动与冲击 2023年16期

常幸, 孙一飞, 邵林媛, 刘庆宽,2,3

(1. 石家庄铁道大学土木工程学院,石家庄 050043;2. 石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;3. 河北省风工程和风能利用工程技术创新中心,石家庄 050043)

随着斜拉桥跨度的逐渐增大,斜拉索上的风荷载对全桥的贡献也越来越大。例如苏通长江公路大桥,斜拉索的风荷载对于主梁位移及内力的贡献,占到全桥风荷载的60%～70%[1]。同时,由于斜拉索的阻尼低、质量轻、刚度小,极易发生不同种类的风致振动。频繁发生的风致振动可能造成斜拉索连接件的疲劳损伤,严重时甚至影响斜拉索的正常使用寿命。因此,如何有效地抑制斜拉索的风致振动,成为桥梁抗风研究的重要课题[2-4]。

斜拉索风雨振由于振幅大、危害严重,受到学者和工程界的广泛关注,采用的振动控制措施有三类,分别是结构措施、机械措施和气动措施,其中,气动措施效果较好,造价较低,应用广泛。气动措施施主要是通过调整斜拉索的截面形状和表面状态,从而改变斜拉索的绕流状态和气动特性,进而减小风致振动。目前最常采用的气动措施有斜拉索表面缠绕螺旋线、设置纵向肋条、设置凹坑等[5]。

与其他气动措施相比,设置纵向肋条具有结构简单、方便安装和耐久性良好等优点。针对纵向肋条的作用,国内外学者进行了相关的研究,Matsumoto等[6]通过风洞试验发现,纵向肋条措施可以阻碍近尾流区二次轴向流的产生,从而保持斜拉索的稳定性;胡圣江等[7]通过风洞试验发现,纵向肋条可以把斜拉索表面的水膜分割成许多小水线,从而阻碍风雨振的产生;李文勃等[8]通过风洞试验发现,螺旋线和纵向肋条的减振效果优于椭圆环;Hung等[9]通过风洞试验的研究发现,纵向肋条措施可以同时有效地抑制风雨激振和干索驰振;毕继红等[10-11]通过数值模拟的研究发现,纵向肋条通过阻碍上水线的形成,从而抑制斜拉索的大幅度振动,但当拉索表面纵向肋条数量过少时,反而会增大拉索振幅。

目前针对纵向肋条的研究,主要集中在控制风雨振方面。最近研究发现,无气动措施或采用了气动措施的斜拉索,其涡激振动的问题受到越来越多的关注,Lankin等[12-13]通过现场实测观察到在无雨中等风速下,斜拉索存在明显的高阶涡激振动;刘志文等[14]通过风洞试验证明在低阻尼条件下双螺旋线斜拉索存在明显的涡激振动现象;Chen等[15]通过风洞试验研究了6.08 m长的斜拉索在不同风廓线下的涡激振动特性,结果表明在不同的风廓线下,斜拉索经常发生单模态或者多模态涡激振动。

同时,设置纵向肋条后斜拉索的气动力特性如何,如何找到既能抑制振动(既包括风雨振,也包括涡激振动)、气动阻力又小的肋条参数,对于研究和工程设计均具有参考意义。基于上述问题,本研究通过风洞试验,研究了不同肋条参数对斜拉索气动力和涡激振动的影响。

1 风洞试验介绍

根据实际斜拉桥斜拉索的统计结果表明:斜拉索直径一般在100～200 mm内,同时考虑风洞试验段尺寸、阻塞度和边界层等方面的要求,确定风洞试验采用直径D为150 mm,长度L为1 700 mm斜拉索作为试验模型,分别进行了测压、测力和测振试验。

试验在石家庄铁道大学风工程研究中心STU-1风洞进行,其中的测振试验在低速试验段进行,其试验段宽4.4 m,高3.0 m,长24.0 m,空风洞最大风速≥30 m/s,湍流度≤0.4%;测压和测力试验在高速试验段进行,其试验段宽2.2 m,高3.0 m,长5.0 m,空风洞最大风速≥80 m/s,湍流度≤0.2%[16]。

如上三类试验的模型尺寸相同,采用有机玻璃管加工而成,保证表面的光滑程度与实际工程中新架设的斜拉索接近。在模型中心设置了具有足够刚度的钢管,钢管和有机玻璃管之间通过系列环向加劲肋连接,保证使模型具有足够的刚度。模型沿轴向布置5圈测压孔,分别为A,B,C,D,E,每圈均匀布置36个测压点。试验模型和测压孔布置图如图1和图2所示。

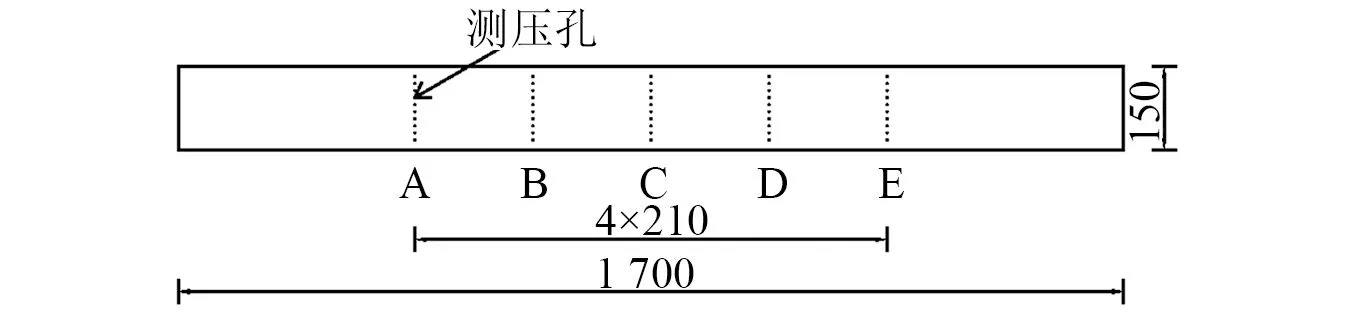
图1 展向测压孔位置示意图(mm)Fig.1 Diagram of spanwise pressure hole position (mm)

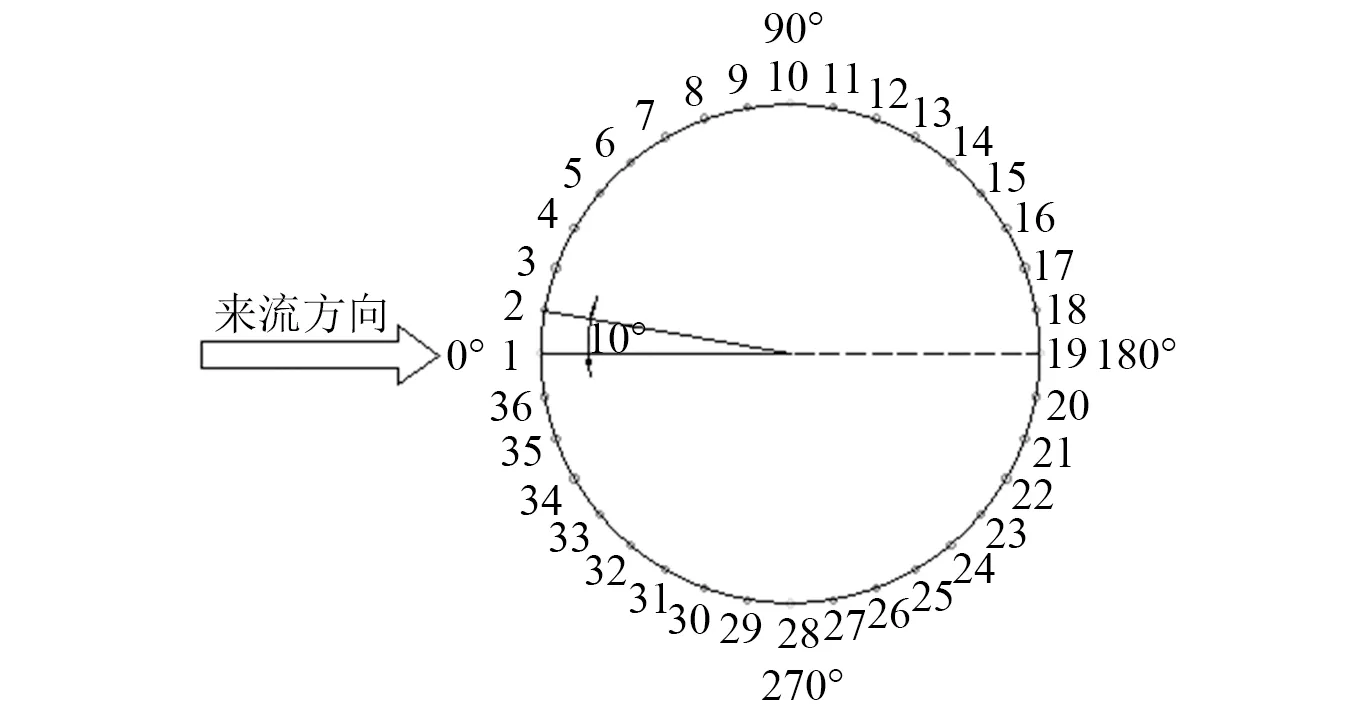
图2 环向测点示意图Fig.2 Diagram of circular measuring points

纵向肋条沿斜拉索模型布置情况如图3所示,肋条高度和宽度均为5 mm,长度为1 700 mm。试验分为两部分:其一是预试验,在较大的肋条角度变化范围内寻找可以控制涡激振动的角度范围,预试验结果表明大于60°夹角时,肋条已经无法很好的控制斜拉索的涡激振动;其二是精确测试试验,在预试验的基础上,对可以控制斜拉索涡激振动的肋条角度范围进行精细化研究。因此,此次试验选取α变化范围为0°～60°,每次间隔5°。为方便描述试验结果,用“位置”的方式对工况进行简化表示,例如5°即代表肋条位置α=5°。

图3 肋条位置示意图Fig.3 Position diagram of ribs

测力和测压试验在高速试验段进行,模型两端安装了补偿模型和5倍斜拉索模型直径的圆形端板,在模型两端各安装一个测力天平,模型通过内置钢管连接到风洞外部的刚臂上。补偿模型位于斜拉索模型两端,直径与斜拉索模型相同,同斜拉索模型之间留有2 mm 左右的空隙,作用一是和端板共同作用,减弱端部效应[17-18],作用二是支撑端板,可以保证补偿模型和端板的气动力不会传递到斜拉索模型上。高速试验段阻塞度为5.8%,测力试验结果采用改进的Maskell法进行阻塞度修正。斜拉索受到的横风向力和顺风向力通过测力天平测得,天平量程为±330 N,测量精度为满量程的0.125%,采样频率为1 500 Hz,采样时间30 s。模型表面通过电子压力扫描阀测得,扫描阀量程为±2 500 Pa,测量精度为满量程的0.15%,采样频率为330 Hz,采样时间60 s。高速试验段的模型实物图和示意图分别如图4和图5所示。

图4 高速试验段模型安装情况Fig.4 Installation of high-speed test section model

图5 高速试验段模型安装示意图Fig.5 Installation diagram of high-speed test section model

图6是无肋条索的平均阻力系数修正前后的对比。由图6可得,阻塞度会使无肋条索的平均阻力系数增大,且在低雷诺数下阻塞度对平均阻力系数的影响更为明显,有必要对测力试验结果进行阻塞度修正。因此,后文中的测力试验结果均进行了阻塞度修正。

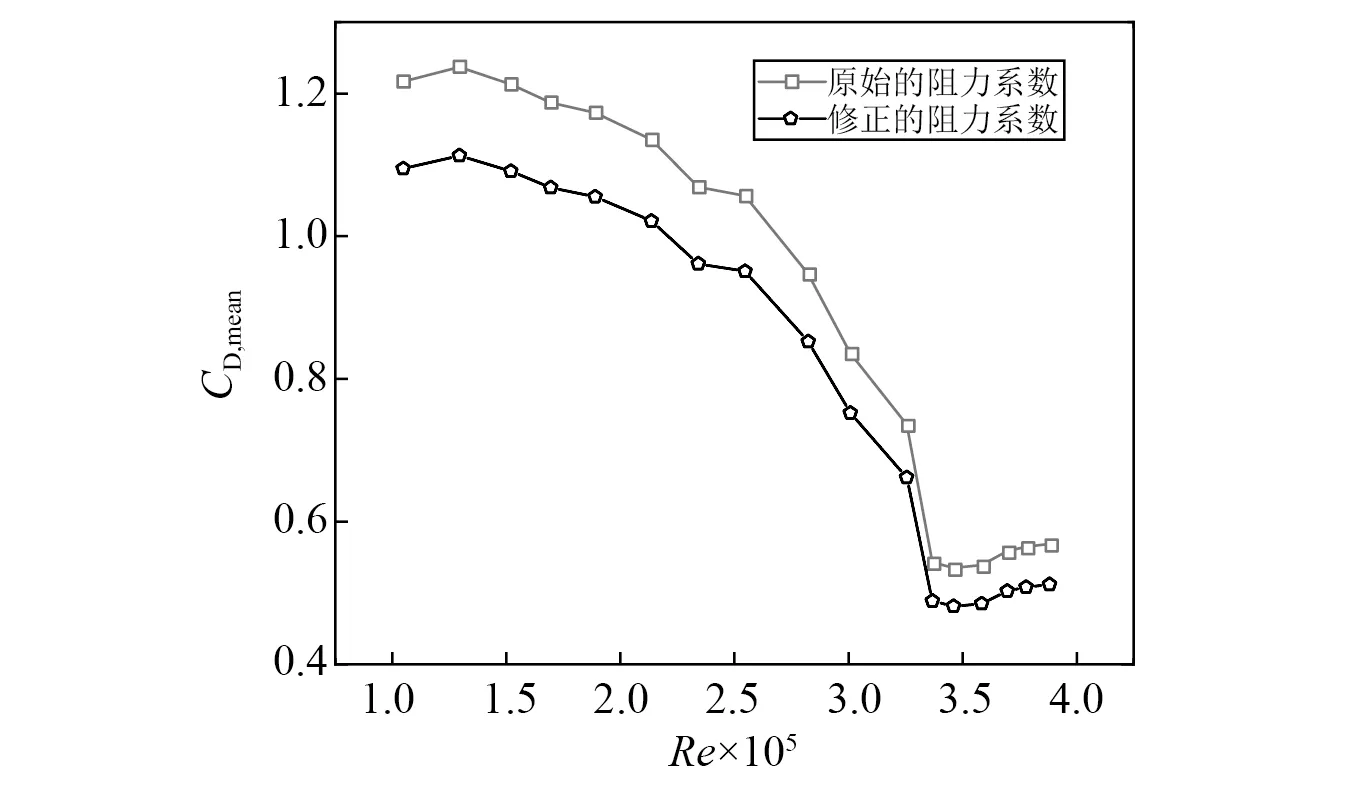
图6 无肋条索的平均阻力系数修正前后对比Fig.6 Comparison of mean drag force coefficients of non-ribbed cable before and after modification

测振试验在低速试验段进行,使用的端板与高速试验段一致。模型两端分别通过4根竖向弹簧连接在刚性框架上,两侧框架对称布置,如图7所示。模型、端板、连接件和弹簧等组成振动系统。在连接件端部位置处安装激光位移计测试振动位移,量程为120±6 mm,采样频率为1 000 Hz,采样时间30 s。振动系统主要参数如表1所示。

表1 振动系统主要参数Tab.1 Main parameters of vibration system

图7 低速试验段模型安装情况Fig.7 Installation of low-speed test section model

2 纵向肋条对斜拉索平均风压分布的影响

测压试验中采用平均风压系数作为风荷载描述的无量纲参数,其表达式为

(1)

式中:Cp,mean为模型表面i号测压孔平均风压系数;p(i)(t)为i号测压孔在t时刻的平均压力;i为测压孔编号,1～36;P为来流静压;U为来流平均风速,通过安装在斜拉索模型上游的眼镜蛇风速仪测得。

试验中雷诺数为流体黏性力与惯性力之比,其表达式为

(2)

式中:D为模型特征尺寸,文中取为斜拉索直径,150 mm;μ为流体动力黏性系数;ν为运动黏性系数; 通过温湿度计和压强计读取温度、湿度以及压强算出μ和ν; 此次试验通过改变风速来改变雷诺数。

将模型表面的5圈测压点的数据进行分析对比,确认结果的一致性,验证模型的二维性、风场的均一性等指标。选用模型中间C圈测点进行详细分析。

图8是无肋条索(光索)的平均风压系数与已有研究结果[19-20]的对比。整体而言,无肋条索的环向平均风压分布变化趋势基本相同,由于风洞阻塞率、雷诺数和模型参数等方面的影响,其数值大小略有差异。

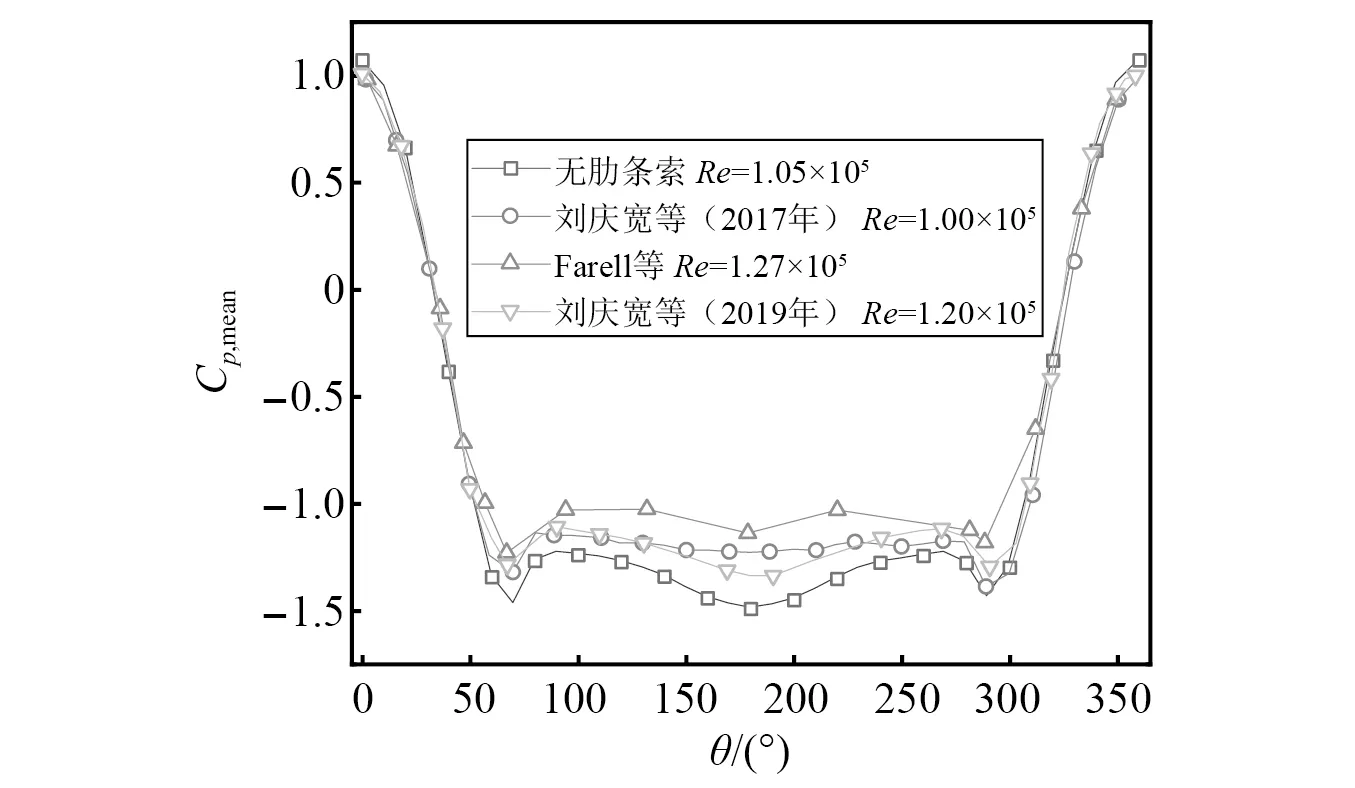
图8 无肋条索的平均风压系数对比Fig.8 Comparison of average wind pressure coefficient of non-ribbed cable

图9是无肋条索环向平均风压系数随雷诺数的变化规律。随着雷诺数的增大,无肋条索周围流体流动依次经历了亚临界区(见图9中Re=1.05×105～2.04×105),单分离泡区(见图9中Re=3.29×105～3.71×105)和双分离泡区(见图9中Re=4.16×105)[21]。在不同流动状态下,无肋条索的环向风压分布呈现出不同的特点:在亚临界区,平均风压分布基本对称,尾部压力系数约为-1.5;在单分离泡区,平均风压分布不再对称,一侧最小风压系数急剧降低,且在该侧产生分离泡,尾部压力系数增大至-0.7左右,尾流区逐渐变窄,此时出现非零的平均升力系数,且平均阻力系数急剧减小;在双分离泡区,另一侧也出现转捩形成的分离泡,平均风压分布再次回归对称分布,尾部压力系数增大至-0.5左右。

图9 无肋条索的平均风压系数Fig.9 Average wind pressure coefficient of non-ribbed cable

图10是不同肋条位置下斜拉索的平均风压系数随雷诺数的变化规律。整体来看,随着肋条位置α的增大,雷诺数对斜拉索模型表面平均风压分布影响逐渐减小,即雷诺数效应逐渐消失。

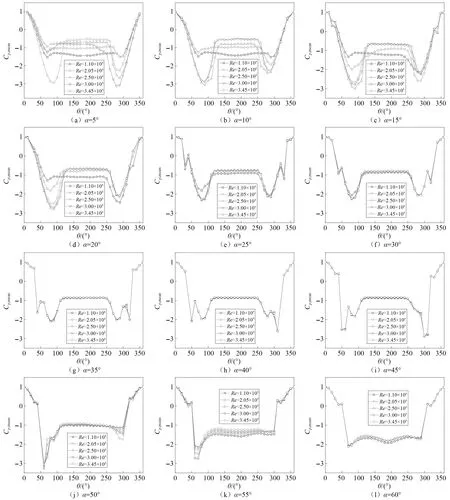
图10 不同肋条位置下斜拉索的平均风压系数随雷诺数的变化规律Fig.10 The variation law of average wind pressure coefficient of stay cable with Re under different rib’s positions

不同位置的肋条,导致对斜拉索模型环向风压分布产生不同的影响。肋条位置α=5°～20°时,斜拉索平均风压系数随雷诺数的变化规律与无肋条索的结果基本一致。对于斜拉索环向平均风压系数不对称状态开始的雷诺数数值,有肋条的比无肋条的小,大位置的比小位置的小,例如,无肋条索在Re=3.29×105时环向平均风压分布开始不对称,5°位置风压不对称开始的Re=2.50×105,而15°位置为Re=2.05×105。

肋条位置大于25°时,雷诺数对平均风压系数没有明显影响,可能是因为流体在模型表面的分离位置被肋条固定导致的;肋条位置α=25°～45°时,肋条对周围测压孔的影响范围比较大,表现为肋条周围的风压会产生突变,肋条前后约10°位置处,平均风压系数有所增大。

3 纵向肋条对斜拉索气动力特性的影响

在测力试验中,斜拉索的升力和阻力直接通过测力天平测得,然后无量纲处理为升、阻力系数,计算公式为

(3)

(4)

式中:CD(t)和CL(t)分别为阻力系数和升力系数时程;FD(t)和FL(t)分别为阻力和升力时程。将CD(t)和CL(t)的平均值定义为平均阻力系数和平均升力系数,分别记为CD,mean和CL,mean。

图11是肋条位置α=5°～30°时斜拉索和无肋条索平均气动力系数随雷诺数的变化。对于无肋条索,随着雷诺数的增大,平均阻力系数曲线经历了一次剧烈的下降。在亚临界雷诺数区(Re≈1.00×105～1.80×105)无肋条索的平均阻力系数约为1.1,由于流场的对称性,这时平均升力系数基本为0。

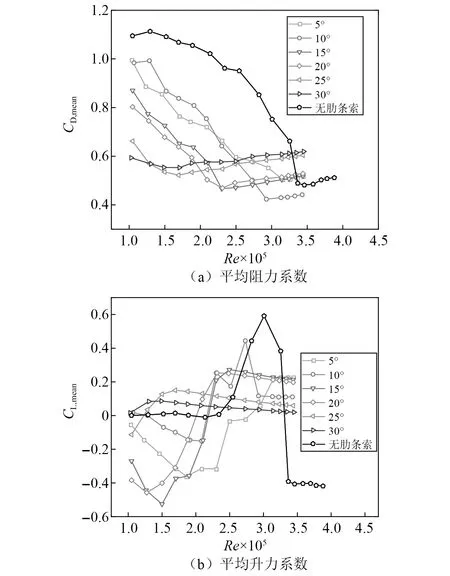
图11 当肋条位置α=5°～30°时斜拉索和无肋条索平均气动力系数随雷诺数的变化Fig.11 Variation of mean aerodynamic coefficients of stay cables and non-ribbed cables with Re when rib’s position α=5°-30°

随着雷诺数的增大,当Re≈1.90×105～3.25×105时,阻力系数急剧下降,这时模型出现非零的升力系数; 当Re≈3.30×105～4.05×105时,平均气动力系数出现一段稳定的平台区,模型的阻力和升力均值会持续稳定。

当肋条位置α=5°～30°时,斜拉索的平均气动力系数整体变化趋势与无肋条索基本一致,但平均阻力系数均小于无肋条索;随着位置α增大,阻力衰减提前出现,并且在低雷诺数下出现平均升力系数;同时,随着位置的增大,平均阻力系数和平均升力系数的稳定范围逐渐变宽,且平均阻力系数的稳定值逐渐增大,平均升力系数的逐渐稳定至0左右,例如当肋条位置α由20°增大至30°时,平均阻力系数的稳定值由0.5增大至0.6左右;平均升力系数的稳定数值则由0.3减小至0附近。

图12是肋条位置α=35°～60°时斜拉索和无肋条索平均气动力系数随雷诺数的变化。整体来看,平均气动力系数不随雷诺数发生改变,与平均风压系数随雷诺数的变化特点一致。

图12 当肋条位置α=35°～60°时斜拉索和无肋条索平均气动力系数随雷诺数的变化Fig.12 Variation of mean aerodynamic coefficients of stay cables and non-ribbed cables with Re when rib’s position α=35°-60°

当肋条位置α=35°～60°时,随着位置的增大,平均阻力系数由0.6增大至1.7左右;当位置为60°时平均阻力系数达到最大值。在肋条位置α=40°,α=50°和α=60°时,斜拉索平均升力系数分别约为0.2和0.3,0.1,而在其他位置下,平均升力系数均稳定在0附近,这些结果同斜拉索表面风压系数的分布规律是一致的。

4 纵向肋条对斜拉索涡激振动特性的影响

图13是无肋条索的涡激振动无量纲振幅A/D(A为振动位移时程的根方差,D为斜拉索模型直径)随折减风速U/fD的变化,无肋条索的涡激振动发生在U/fD=4.63～7.03内,在此锁定区间内,最大无量纲振幅约为A/D=0.123,对应的折减风速为5.84。

图13 无肋条索的涡激振动无量纲位移随折减风速的变化Fig.13 Variation of dimensionless displacement of vortex-induced vibration of non-ribbed cable with reduced wind speed

图14是典型折减风速下无肋条索涡激振动的位移时程和功率谱密度(power spectral density,PSD),分别为刚进入涡激锁定区间时、最大振幅和刚退出涡激锁定区间时,对应图13中的分析点1～3。从图14中可以看出: 当U/fD=5.84时,振动位移随着时间变化非常稳定,接近标准的正弦曲线;而当U/fD=4.63和U/fD=7.03时,振动位移的幅值随时间发生明显的变化,三个折减风速下的PSD均保持着相同的卓越频率3.29 Hz,与振动系统的自振频率一致。同时,可以观察到,除了卓越频率3.29 Hz外,在4.2 Hz和5.3 Hz处也有两个小的频谱峰值(在U/fD=5.84时更为明显),Raghavan等[22-25]在风洞试验中均观察到该现象,并分析其原因认为是由于振动系统非线性特性的振动频率引起的。

图14 典型折减风速下无肋条索涡激振动位移时程与PSDFig.14 Displacement time history and PSD of vortex-induced vibration of non-ribbed cable under typical reduced wind speed

为了定量分析肋条位置对斜拉索涡激振动的控制效果,定义最大振幅降低率NE1和锁定区间减小率NE2如下

(5)

(6)

式中:AM为无肋条索振动位移时程的根方差最大值;AGM为不同肋条位置下斜拉索模型振动位移时程的根方差最大值;IM为无肋条索锁定区间的范围;IGM为不同肋条位置下斜拉索锁定区间的范围。由式(5)和式(6)可以得到,无肋条索的NE1和NE2均为0,NE1或NE2>0代表肋条对斜拉索的涡激振动有抑制作用,NE1或NE2<0则表示肋条对涡激振动有放大作用。

图15分别是肋条位置α=5°～30°时,斜拉索涡激振动无量纲位移随折减风速的变化、肋条位置对斜拉索涡激振动最大振幅的影响和肋条位置对斜拉索涡激振动锁定区间的影响。

图15 当肋条位置α=5°～30°时斜拉索涡激振动的变化情况Fig.15 Variation of vortex-induced vibration of stay cables with rib’s position α=5°-30°

由图15(a)可知,有肋条斜拉索的涡激振动响应与无肋条索较为接近:未进入振动区间时,无量纲振幅A/D基本为零;进入振动区间后,A/D随U/fD的增大逐渐增大,达到最大振幅后,A/D随U/fD的增大逐渐减小;退出振动区间后,A/D再次回归至零附近。

由图15(b)和图15(c)可知,在肋条位置α=5°～30°时,布置肋条后斜拉索涡激振动的最大振幅均有所减小,其中20°时最大振幅减小最少,约为5.7%,在其他肋条位置下,最大振幅均减小约为20%。同时,肋条位置为15°时,肋条放大了斜拉索涡激振动的锁定区间,其余位置下的肋条均在一定程度上缩短了斜拉索涡激振动的锁定区间。在此类肋条位置下斜拉索的涡激振动变化范围并不太明显。

图16分别是肋条位置α=35°～60°时,斜拉索涡激振动无量纲位移随折减风速的变化、肋条位置对斜拉索涡激振动最大振幅的影响和肋条位置对斜拉索涡激振动锁定区间的影响。

图16 当肋条位置α=35°～60°时斜拉索涡激振动的变化情况Fig.16 Variation of vortex-induced vibration of stay cables with rib’s position α=35°-60°

由图16(a)可知,在肋条位置α=35°～50°时,随着位置的增大,斜拉索涡激振动的锁定区间逐渐向低风速方向移动,当55°时,涡激振动被完全抑制。

由图16(a)和图16(c)可知,在肋条位置α=35°～60°时,肋条的出现均对斜拉索涡激振动的最大振幅均有所抑制。其中55°时完全不会振动,40°最大振幅减小约为40%,在其他肋条位置下,最大振幅均减小约为22%。在35°和40°时,涡激振动的锁定区间有所放大,在45°和50°时,涡激振动的锁定区间均有减小,在60°时涡激振动的锁定区间范围被扩大约116%。