滚珠丝杠式燃气舵结构仿真与运动控制

刘静怡, 郑 健, 魏岩淞

(1. 南京理工大学 机械工程学院,南京 210094;2. 空间电子信息技术研究院,西安 710000)

燃气舵作为导弹实现大攻角推力矢量控制的关键机构,能够实现俯仰、偏航、滚转三个方向的控制[1]。由于电动舵机具有可靠性高、使用维护简便,制造、装调难度较低等优点,现有的燃气舵舵机系统通常采用电动舵机[2],电动舵机系统主要由电机、减速传动机构、基座、舵片组成。舵机的输出位置精度会直接影响产生的气动力和气动力矩,从而影响弹体上固体火箭发动机所获得侧向力的大小和弹体的航向校正,因此需要对舵机的运动实现精确控制,保证燃气舵的矢量控制性能和导弹的机动性能。舵机系统工作启动瞬间,由于舵片的气动力加载和电机的启动加速度,传动机构会受到很大的冲击力,极大地影响了机械结构的可靠性,因此需要对舵机系统启动瞬间传动机构的动力学相应展开研究。

研究结构在动态载荷作用下所表现的动态特性与动态响应属于结构动力学研究内容。结构动力学问题有两个重要特点[3]:第一个是动态载荷及其结构的响应随时间变化,分析者要相应于响应历程在所有感兴趣的时间内求得响应解;第二个更为重要的特点是加速度在分析中占据重要作用,加速度引起结构的分布惯性力,通常惯性力表示为与结构内弹性力相平衡的总载荷的一个重要组成部分,因而在求解动力学问题时,必须考虑惯性力的作用,只有在结构运动非常缓慢、运动惯性力非常小时才可忽略不计。

倪迎鸽等[4]将有理函数近似导出的折叠运动中的非定常气动力引入到动力学控制方程中,获得了机翼折叠运动中在时变气动力作用下的瞬态动力学响应。李彪等[5]基于非线性分析软件ABAQUS对微小型卫星的捕获帽结构及其固定形式展开冲击动力学特性研究,定位解锁装置薄弱环节并验证。周军等[6]提出了一种基于ADAMS自定义函数的发射动力学仿真方法,使火炮发射时的内弹道过程与制退后坐运动同时在ADAMS 软件内部进行动力学求解。

本文针对所设计的滚珠丝杠式燃气舵展开研究,采用ADAMS对传动机构进行运动学仿真和多刚体系统动力学仿真,分析在不同启动响应时间下零件的接触力,并根据ADAMS分析结果在ANSYS软件中对危险零件进行瞬态动力学分析,得到其动应力响应。最后基于运动学仿真结果,针对燃气舵的单片舵舵偏装置进行硬件控制平台设计与搭建,采用MATLAB Simulink仿真和试验验证实现对舵片运动的闭环比例-积分-微分(proportional-integral-derivative,PID)控制。

1 燃气舵结构建模与仿真

1.1 燃气舵结构与传动机构简化建模

本文设计的燃气舵舵机系统采用滚珠丝杠式传动机构,具体设计图如图1所示。舵片呈十字型布局,四组相互独立的传动机构灵活操纵舵片偏转,从而调整导弹的飞行姿态。其中滚珠丝杠的直径为8 mm,螺距为2 mm,行程约为12 mm。伺服电机通过联轴器与滚珠丝杠相连,滚珠丝杠将旋转运动转化为丝杠螺母的直线运动,丝杠螺母通过滑块与拨叉机构刚性连接,带动舵片偏转。与传统的齿轮传动机构相比,滚珠丝杠式传动机构间隙小、轴向刚度高,具有更高的控制精度,且将滑动摩擦变为滚动摩擦,摩擦损耗小,极大地提高了系统的工作效率[7]。

图1 滚珠丝杠式燃气舵舵机Fig.1 Ball screw gas rudder actuator

为了研究舵机系统传动机构在启动瞬间受到的冲击力,需要在ADAMS中对传动系统进行动力学分析,首先对滚珠丝杠式传动机构进行简化建模,简化后的传动机构包括滚珠丝杠、固定座、支撑座、第一导轨、第二导轨、滑块、作动杆、销轴、拨叉和舵片。ADAMS中简化后的模型如图2所示。其中固定座、支撑座和滑块的材料为铝合金,其余零件的材料为钢。

图2 传动机构简化模型Fig.2 Simplified model of transmission mechanism

1.2 燃气舵减速传动机构动力学分析

在燃气舵舵机系统冲击过程中,结构与载荷互相耦合,传动系统各零件间作用的载荷随时间和结构变形而变化。ADAMS通过CONTACT定义冲击模型,利用 Impact 冲击函数来计算构件的冲击载荷,该函数主要两部分组成,一个是由于两构建相互切入而产生的弹性力;另一个是由相对速度产生的阻尼力。当两构件连续接触时,系统将接触定义为非线性弹簧模型,构件材料的弹性模量相当于弹簧的刚度,阻尼即为能量损失[8]。使用Impact函数时需要输入刚度系数、力的非线性指数、最大黏滞阻尼系数、最大阻尼时构件变形深度。根据Hertz接触理论[9],等效刚度K的计算公式如下

(1)

式中:R1,R2分别为碰撞点处两物体的曲率半径;σ1,σ2为材料的相关参数,其计算式为

(2)

式中:νI为材料的泊松比;EI为材料的弹性模量。

阻尼系数D与最大阻尼时构件变形深度δ的关系可表示为

D=χδn

(3)

式中,χ为滞后阻尼因子,可表示为

(4)

在燃气舵舵机系统启动瞬间,除了冲击力,舵片还承受较大的空气动力载荷,即铰链力矩[10]。由于舵片正转和反转时工作情况对称,故本文针对舵片正转展开研究。由Fluent软件对本文舵片的三维流场进行仿真分析,给定入口边界条件为:总压条件为6 MPa、总温条件为300 K,对应的质量流率为0.353 6 kg/s;出口边界为压力出口,出口反压1.01×105Pa,温度300 K;壁面为无滑移绝热壁;湍流模型选用单方程SA (spalart-allmaras) 模型。得到舵片受到的铰链力矩如表1所示。

表1 不同工况下舵片的铰链力矩Tab.1 Hinge moment of rudder blade under different working conditions

对表1中数据用多项式拟合得到铰链力矩和舵偏角的关系如下

f(x)=0.034 08x2-4.636x+0.337 6

(5)

将上述关系写入ADAMS的函数编辑器中将铰链力矩施加在舵片上,并通过step函数对滑块的位移进行控制,使舵片从0°偏转到20°,对舵片施加的铰链力矩如图3所示。

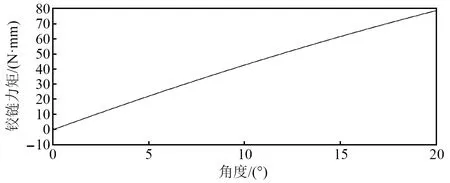
图3 舵片的铰链力矩Fig.3 Hinge moment of rudder blade

启动响应时间分别为0.05 s,0.10 s,0.15 s时,对传动机构展开动力学分析。设置仿真时间为0.2 s,步数为100。仿真得到滑块的速度和加速度分别如图4和图5所示,滑块的驱动力如图6所示,各相邻零件的接触力如图7所示。

图4 不同响应时间下滑块的速度Fig.4 The speed of the slider at different response times

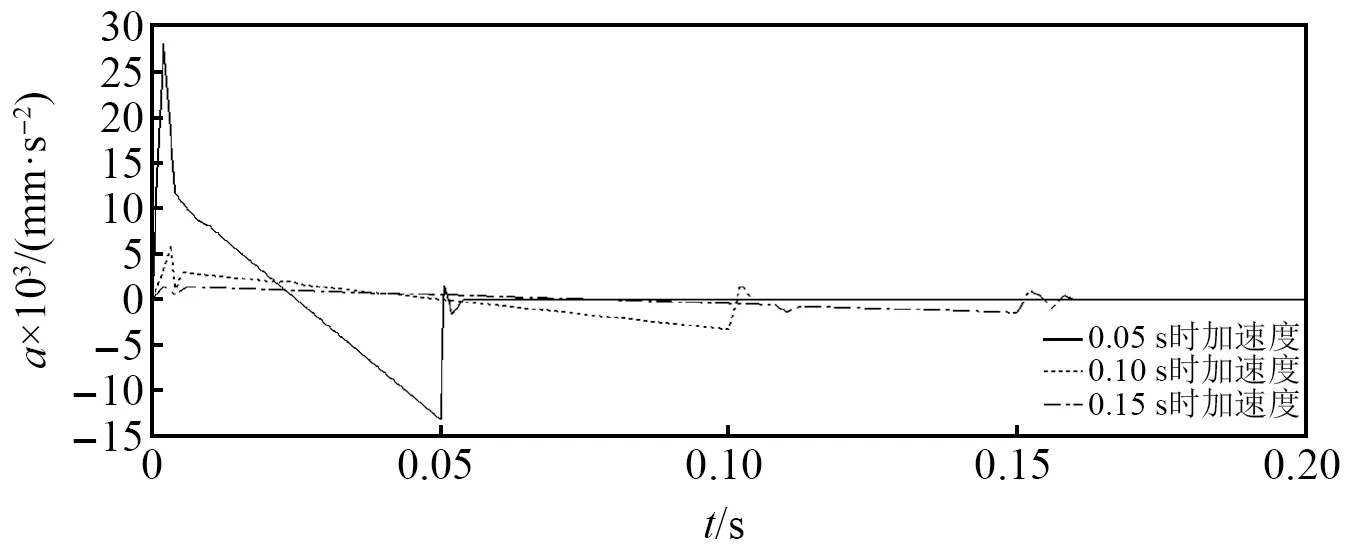
图5 不同响应时间下滑块的加速度Fig.5 The acceleration of the slider at different response times

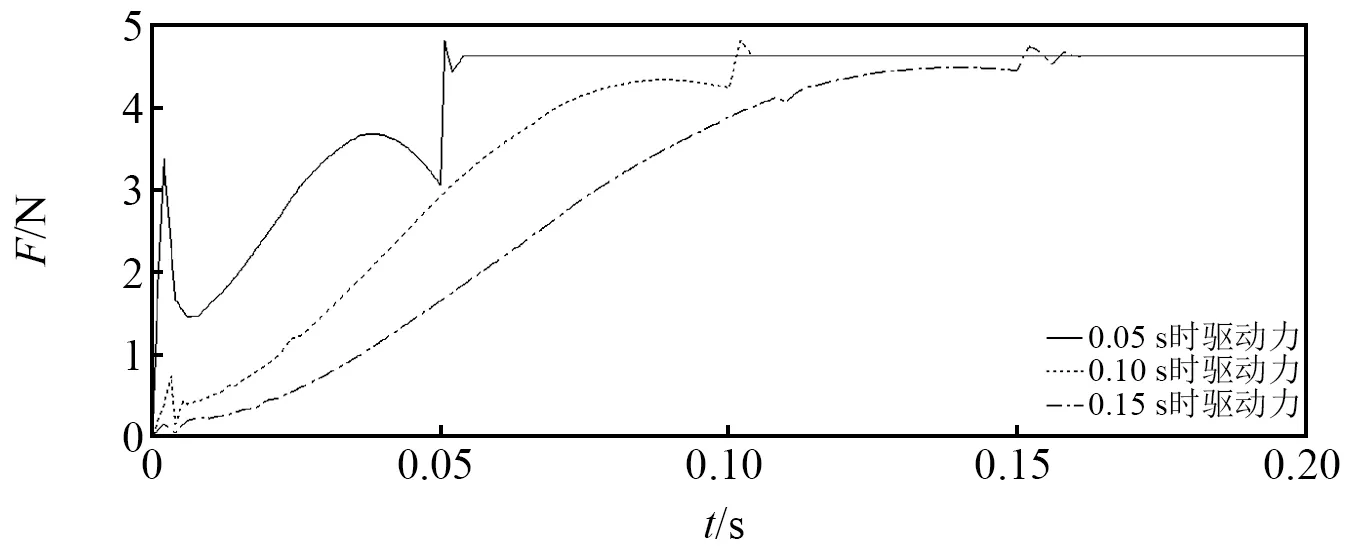
图6 不同响应时间下滑块的驱动力Fig.6 The driving force of the slider at different response times

图7 不同响应时间下相邻零件的接触力Fig.7 Contact force of adjacent parts under different response times

由图4～图6可知,驱动力曲线的突变点对应加速度曲线的突变点,启动结束后,驱动力均稳定在4.64 N。当响应时间分别为0.05 s,0.10 s,0.15 s时,滑块的最大速度分别达到165 mm/s,83 mm/s,55 mm/s;最大加速度分别达到28 051 mm/s2,5 949 mm/s2,1 439 mm/s2。

电机与滑块的速度和加速度存在如下关系

(6)

(7)

式中:nmotor为电机转速;vb为滑块速度;Ph为滚珠丝杠导程;αmotor为电机加速度;ab为滑块加速度。

相应地,电机的最大转速分别为4 950 r/min,2 490 r/min,1 650 r/min,最大加速度分别为8.415 3×105r/min/s,1.784 7×105r/min/s,4.317 0×104r/min/s。

当响应时间分别为0.05 s,0.10 s,0.15 s时,响应时间不同,各接触力随响应时间的增加响应速度变慢,但各接触力的最大值和最小值分别基本保持一致。

作动杆和滑块、拨叉和舵轴的接触力振动明显,作动杆和销轴、销轴和拨叉的接触力曲线平滑,分析是因为作动杆和滑块、拨叉和舵轴均为固定连接;而作动杆和销轴、销轴和拨叉之间存在相对位移,摩擦力占据接触力的较大比重。

作动杆和滑块的接触力在启动时约为122.78 N,即为最大值,在响应时间内有较大振荡,响应时间越快频率越高,但振幅无明显变化,响应结束后稳定在82.52 N,也即最小值。作动杆和销轴的接触力约为12.02 N,在启动和稳定后无明显变化。销轴和拨叉的接触力在启动后和接近稳定时存在小幅抖动,最终稳定在4.95 N。拨叉和舵轴的接触力在响应时间的前一半振动明显,在响应时间的后一半趋于稳定,且响应时间越快振动越明显,最大值约为95 N。

1.3 危险零件瞬态动力学分析

根据接触力分析情况,认为作动杆为危险零件。将ADAMS中得到的时间函数的载荷输入ANSYS Workbench进行瞬态动力学分析,可以得到危险零件的动力响应。本文采用Newmark时间积分法分析求解燃气舵传动机构危险零件的瞬态动力学特性。

设置仿真时间为0.2 s,步数为100步,以响应时间0.1 s为例,得到危险零件的应力云图,提取每个载荷步的最大应力值,得到危险零件最大动应力随时间的变化图,如图8所示,并通过提取每个载荷步的燃气舵最大变形值,得到最大变形量曲线。

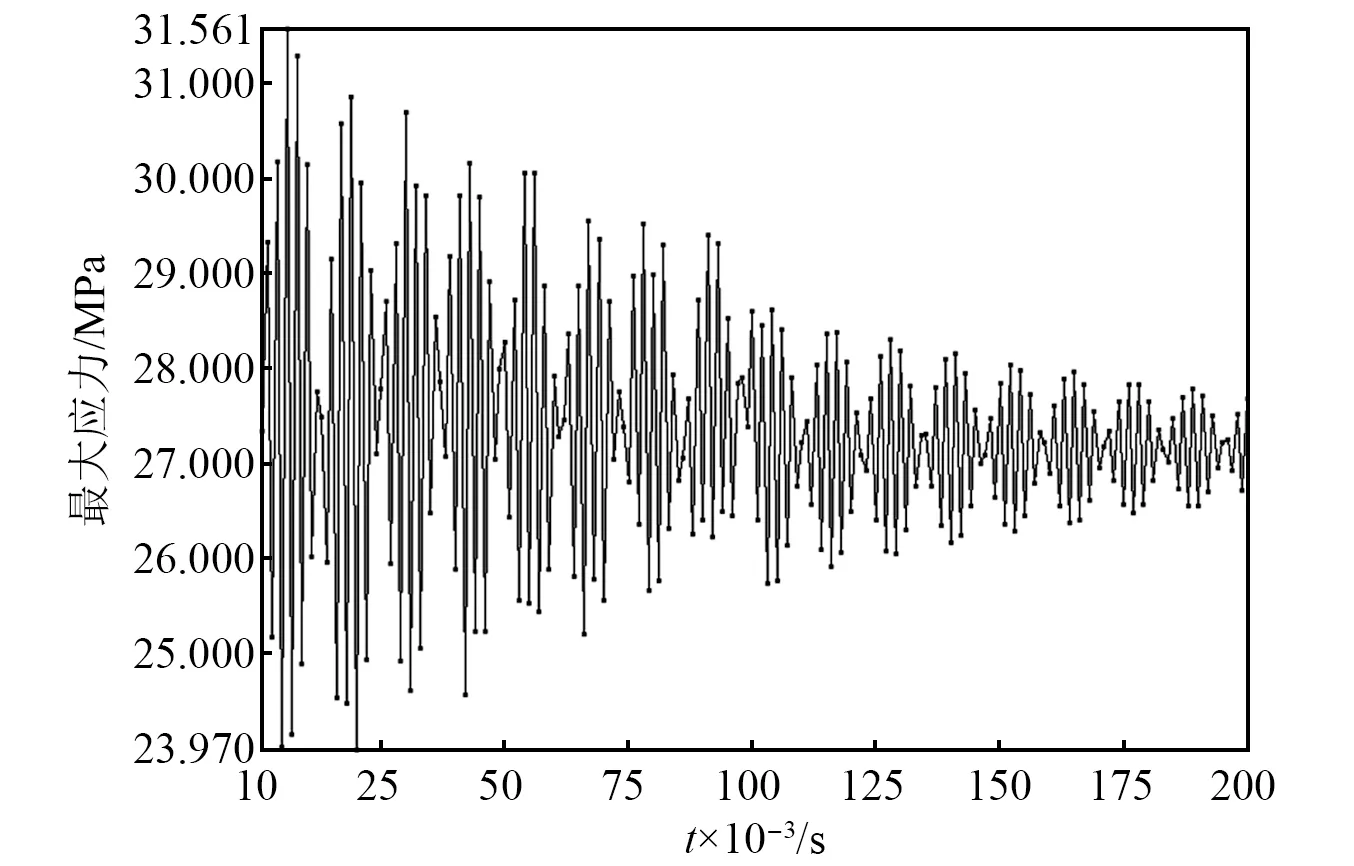
图8 0.10 s响应时间下作动杆最大应力曲线Fig.8 Maximum stress curve of actuating rod under 0.10 s response time

作动杆的最大应力振荡明显,随着时间的增加呈衰减趋势,最大应力出现在0.006 s,约为31.561 MPa,最终收敛于27.5 MPa左右,整体远小于钢的屈服极限250 MPa,故作动杆的强度满足设计要求。图9为应力最大时作动杆的应力云图。由图9可知,作动杆在凸台处存在轻微应力集中,此结构已设置圆角减小应力集中,足以达到良好的使用效果。作动杆的最大变形曲线与最大应力曲线趋势相同,最大变形也出现在0.006 s,约为24.469 μm,相对于作动杆的整体尺寸而言极为微小,可知该传动机构具有良好的尺寸稳定性。

图9 0.10 s响应时间下t=0.006 s作动杆应力云图Fig.9 Stress cloud diagram of actuating rod at t=0.006 s under 0.10 s response time

图10 0.10 s响应时间下作动杆最大变形量曲线Fig.10 The maximum deformation curve of the actuating rod under 0.10 s response time

2 燃气舵控制平台设计

2.1 舵机系统控制原理

确定结构设计可行后,针对燃气舵单片舵舵偏系统进行控制平台设计,实现对单片舵的运动控制。燃气舵电动舵机系统闭环控制原理图,如图11所示。将角度指令发送至控制器中,通过某种控制算法作用于伺服电机,驱动伺服电机偏转相应的角度,并通过传动机构控制舵片偏转,利用角度反馈装置实时检测舵片的位置,且将实际角度反馈至控制器,实现系统的闭环控制。

图11 燃气舵电动舵机系统闭环控制原理图Fig.11 Schematic diagram of closed-loop control of gas rudder electro-mechanical actuator system

PID控制通过控制误差值的比例、积分、微分来控制被控量,作为最早发展起来的控制策略之一,PID由于其算法简单、鲁棒性好和可靠性高,被广泛应用于工业过程控制,至今仍然是最常使用的控制算法之一。本文采用PID算法实现对舵片运动的闭环控制,驱动器采用无刷直流伺服电机,角度反馈装置选用旋转编码器。

2.2 舵机系统数学模型

利用MATLAB的System Identification工具箱辨识无刷直流电机的数学模型。辨识是指基于一个系统的输入输出数据,从一组给定的模型类中,确定一个与所测系统等价的模型[11]。System Identification的辨识计算过程是一个模型参数迭代的过程,方法包括最大似然、预测误差最小化 (prediction error minimization,PEM) 和子空间系统辨识。工具箱可以使用时域和频域输入-输出数据来辨识连续时间或离散时间模型,如传递函数、过程模型和状态空间模型等线性系统辨识;对于非线性系统动态特性辨识,可以使用Hammerstein-Weiner模型和NARX模型,NARX指由外部输入的非线性自回归模型,包括小波网络、树分类、sigmoid 网络等。对于系统的机理不是完全未知的情况,可以利用已有的理论定义含参的模型框架,然后通过灰盒方法进行模型参数辨识。

已知无刷直流电机可等效为二阶系统。采集500组电机开环控制的输入输出数据作为样本,在工具箱中选择传递函数辨识。连续时间下,单输入单输出系统(single-input single-output,SISO)传递函数模型的表达形式为

Y(s)=G(s)U(s)+E(s)

(8)

(9)

式中:Y(s),U(s)和E(s)分别为输出、输入和噪声的拉普拉斯变换;G(s)为输入和输出之间的关系; num(s)和den(s)分别为分子和分母多项式。

工具箱分别尝试IV,SVF,N4SID,GPMF算法初始化分子分母参数值,且自动选择预测误差范数最小的方法。最终得到本文无刷直流伺服电机的传递函数如下

(10)

滚珠丝杠式传动机构的工作原理,如图12所示。以丝杠螺母向右运动为正方向,此时拨叉向右摆动,令电机偏转的角度为θmotor,舵片偏转角度为θ,拨叉的摆动半径为L,丝杠导程为Ph,由三角函数关系可知

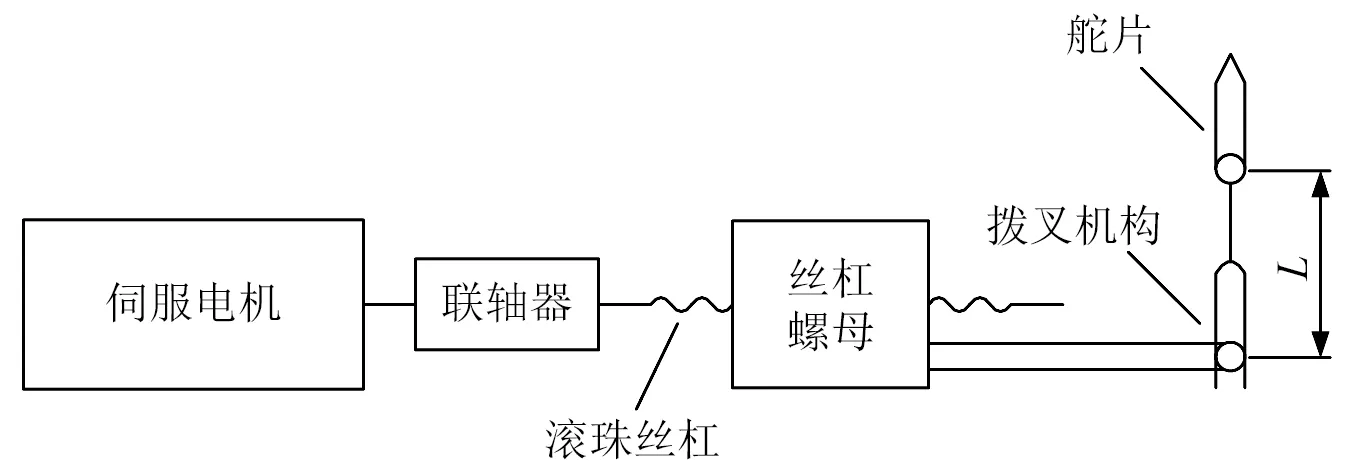
图12 燃气舵电动舵机系统传动机构示意图Fig.12 Schematic diagram of transmission mechanism of gas rudder electro-mechanical actuator system

(11)

2.3 燃气舵系统仿真

在MATLAB Simulink中搭建系统的仿真模型,如图13所示,对燃气舵理想舵偏角和实际舵偏角的差值进行PID调节。PID的比例参数KP实时反映系统的偏差,增大KP可以加快系统的动态响应,但超调量变大,KP过大会使系统不稳定;积分参数KI为积分时间常数TI的倒数,可以消除静差,通常在其他条件不变时,TI越大积分作用越弱,系统的超调量越小,但响应速度变慢;微分参数KD反映系统偏差信号的变化率,可以在偏差出现之进行超前调节,从而加快系统的响应速度,减少调节时间。根据工程经验整定,先由0逐步增大KP,由较大值逐步减小KI,最后加入KD进行微调,使系统达到要求。最终选取比例、积分、微分的参数分别为KP=17,KI=1 370,KD=0.05,得到系统的阶跃响应结果和正弦信号跟踪仿真结果分别如图14和图15所示。

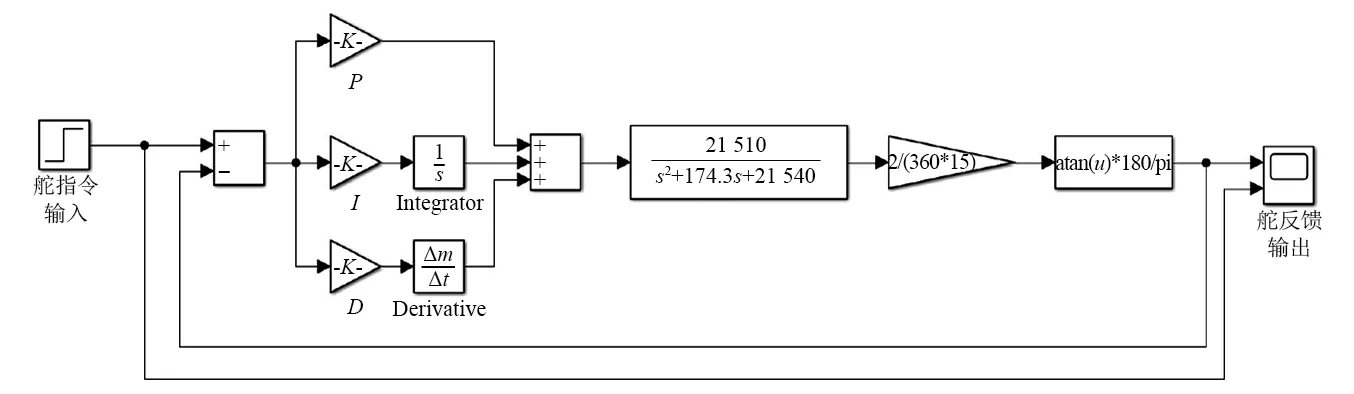
图13 燃气舵电动舵机系统控制框图Fig.13 Control block diagram of gas rudder electro-mechanical actuator system

图14 燃气舵舵机系统阶跃响应仿真结果Fig.14 Simulation results of step response of gas rudder actuator system

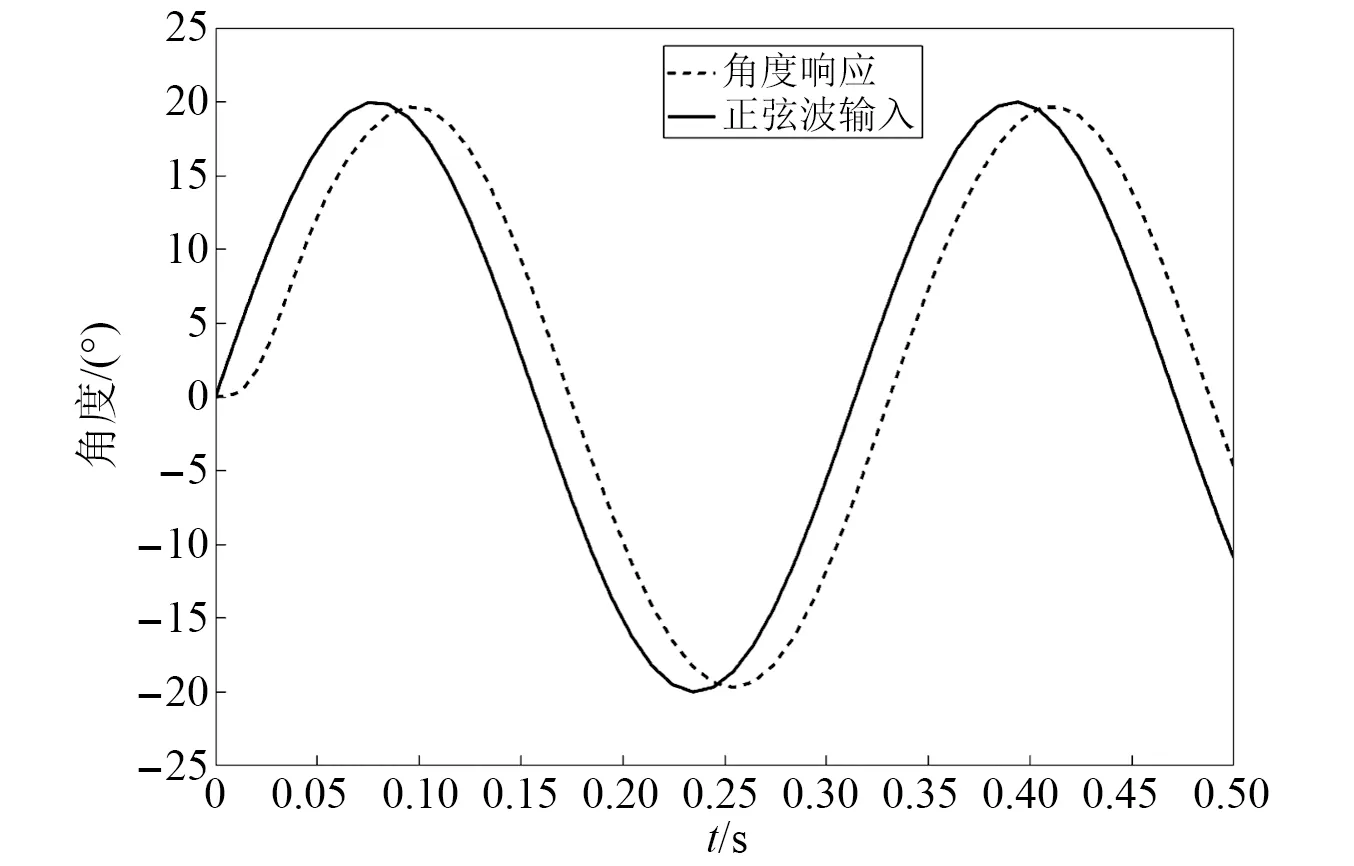
图15 燃气舵舵机系统正弦信号跟踪仿真结果Fig.15 Simulation results of sine signal tracking of gas rudder actuator system

PID控制的上升时间为20 ms,超调量约为5%。对于20° 20 Hz的正弦信号跟踪,实际舵偏角相对于理想舵偏角在幅值上存在约0.3°的偏差,相位移约15 ms。总体来说,该系统的PID控制处于较高水平。

3 燃气舵单片舵舵偏系统试验

搭建燃气舵系统硬件控制平台,进行空载条件下单片舵舵偏系统PID闭环控制试验,测试舵片偏角的响应性能。

将PID参数写入电机控制代码中,伺服电机使用位置模式,根据ADAMS运动学分析结果,设置电机的加速度为8 000 r/min/s,转速为3 000 r/min。依次给定舵机偏转指令8°和16°,得到舵偏角连续阶跃变化曲线,结果如表2所示。

表2 舵片偏角PID控制试验结果Tab.2 Experimental results of the PID control of the deflection angle of the rudder blade

舵偏指令为8°和16°时的PID控制结果,超调量、稳定角度误差和上升时间相差不大,但16°时的调节时间明显大于8°。由于传动机构存在间隙,系统的试验响应结果和仿真结果相比存在一定滞后。由图16可知,系统的实际采样值存在小幅抖动,可以看出系统抵抗干扰的能力一般,但当干扰小时能够达到较好的控制效果。

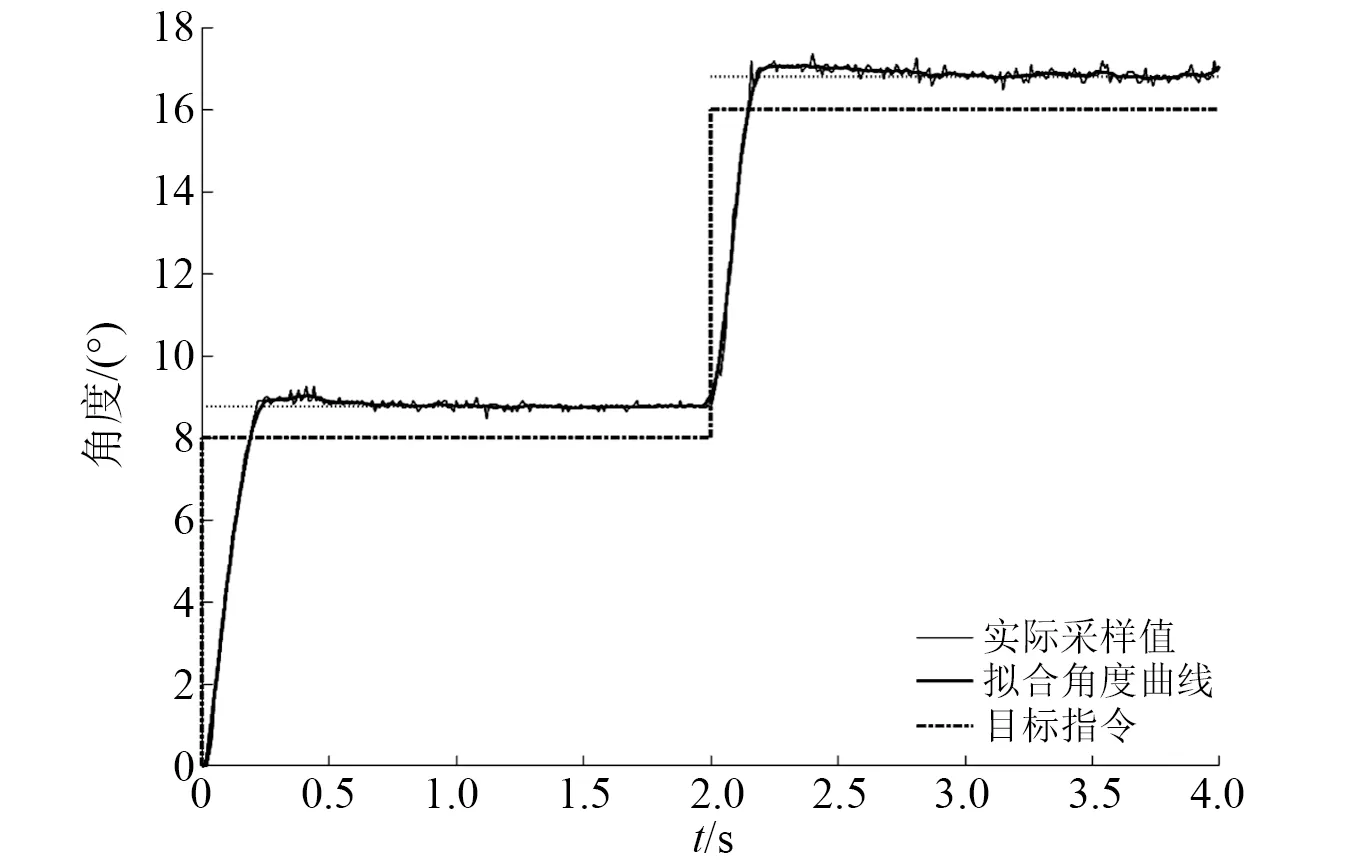
图16 舵偏角8°和16°时的阶跃变化曲线Fig.16 Step change curves for rudder deflection angles of 8°and 16°

4 结 论

(1) 基于ADAMS对传动机构进行运动学仿真和多刚体系统动力学仿真,得到了不同启动响应时间下舵片的速度、加速度曲线和零件的冲击力曲线,利用动力学仿真结果在ANSYS中对危险零件进行瞬态动力学分析,得到其应力云图、最大动应力曲线和最大变形量曲线。

(2) 建立了燃气舵系统的数学模型,在MATLAB Simulink进行系统的PID控制仿真,并利用试验验证了单片舵的PID闭环运动控制能够达到较好的控制效果。