大跨度钢管混凝土劲性骨架拱桥地震易损性分析

王志远, 赵人达, 吴鑫睿, 赵成功

(西南交通大学 土木工程学院,成都 610031)

钢管混凝土劲性骨架拱桥是以钢管混凝土为劲性骨架,外挂模板分段分环浇筑外包混凝土形成主拱结构的大跨度钢筋混凝土拱桥,具有跨越能力大、变形小特点与优越的结构动力性能,是我国西南山区最具竞争力的高速铁路大跨度桥型之一[1]。其适用范围必将随着西南地区高速铁路的快速建设而拓展至更高地震烈度地区,开展劲性骨架拱桥的抗震性能研究对其未来发展与应用具有重要的实际意义。

目前劲性骨架拱桥的桥例均建成较晚,同时桥址避开高烈度区域,缺乏震害案例参考。历史震后调查表明,钢筋混凝土拱桥的总体震害为拱圈断裂和开裂、拱上立柱开裂,甚至全桥损毁;拱脚与L/4拱处的截面弯矩最大,是抗震的薄弱环节之一;拱脚处于形状突出部位,既可能出现弯曲开裂,又可能形成剪切位移[2-3]。然而上述震害经验对劲性骨架拱桥是否适用仍有待商榷。刘珍等[4-5]通过反应谱分析与时程分析方法,总结了在地震作用下拱桥的位移和内力规律,研究了其在不同地震工况及不同地震波作用下的受力特性。Shao等[6]对铁路大跨度劲性骨架拱桥的抗震基本原理和方法进行了研究,旨在更新现行的铁路工程抗震规范中的设计方法,并对比了基于延性设计和混合隔震设计的结构抗震性能。邹建波[7]研究了防屈曲支撑对劲性骨架拱桥的减震效果,得出合理的顺、横桥向减震设计方案。谢松茂[8]设计了摩擦摆支座加阻尼器的减隔震方案,在控制墩梁位移的同时能够均衡地分配拱上立柱底部的弯矩和剪力。Zhao等[9]研究了非平截面应力对劲性骨架拱桥抗震性能的影响,表明忽略施工过程将会低估拱圈混凝土开裂和钢筋屈服的损伤风险。综合研究现状发现,目前对于劲性骨架拱桥的抗震研究主要集中在结构响应及控制方面,但是对于其地震损伤评估模型和方法的探究则较少涉及。

地震易损性分析是一种基于概率的桥梁结构抗震性能评估方法,能宏观地反映地震动强度与结构破坏程度之间的关系[10]。借助易损性分析方法对拱桥开展地震损伤评价,可以从概率的角度定量地描述桥梁结构的损伤可能,并确定结构的薄弱部位,从而为抗震加固、风险评估等研究提供必要依据。国内外学者[11-13]对连续刚构桥、钢管混凝土拱桥、斜拉桥等桥型的地震易损性研究已经较为完备,而针对劲性骨架拱桥的易损性研究亟待进行。值得说明的是,如何对劲性骨架拱桥主要控制构件的易损性进行合理、全面的分析仍需深入探讨,针对由钢管混凝土骨架及其外包混凝土组成的组合结构拱肋的损伤指标和评价方法更是鲜有报道。

鉴于上述问题,本文以一座高速铁路上承式钢管混凝土劲性骨架拱桥为工程实例开展同种桥型的地震易损性研究。首先建立OpenSEES桥梁非线性数值模型,通过动力时程分析与增量动力分析 (incremental dynamic analysis, IDA)对该桥梁控制构件的地震损伤进行评估,并引入Copula函数建立主拱肋构件系统的易损性曲线。研究方法与研究结果可供同类型高速铁路桥梁地震损伤评估参考,同时对其后续的抗震减震研究具有一定的指导意义。

1 劲性骨架拱桥模型

1.1 工程概况

本文以一座跨度为340 m的上承式高速铁路钢管混凝土劲性骨架拱桥为研究对象,其结构如图1所示。该拱桥竖直平面内矢高74 m,矢跨比为1/4.595,拱轴线采用拱轴系数m=3.2的悬链线。主拱圈平面为提篮形,采用箱型肋拱截面,分叉段拱肋截面为单箱单室截面,拱圈合并段为单箱三室截面。主拱肋箱体纵向高度按1.5次抛物线关系变化,由拱脚处高11.0 m变至拱顶处高6.0 m。拱肋劲性骨架上下弦杆采用钢管混凝土构件,上下弦主钢管共计8肢,管内灌注自密实无收缩C60混凝土,主钢管与横联钢管材质采用Q390D钢材。主钢管间横向、竖向通过腹杆、平联杆等联结系形成整体空间桁架结构,材质采用Q345D钢材。横联钢管与其他联结杆件共同构成两组拱肋之间的横向联结系。主钢管与拱肋分叉段横联钢管为Φ750×24 mm,拱顶合并段横联钢管为Φ560×16 mm,其他联结杆件为四肢组合角钢结构。主拱圈采用劲性骨架法外包C55补偿收缩混凝土施工。交界墩和拱上立柱均采用双柱式桥墩,拱上结构为3联4跨预应力混凝土连续梁。拱脚基础由水平桩基础和竖直桩基础组成。

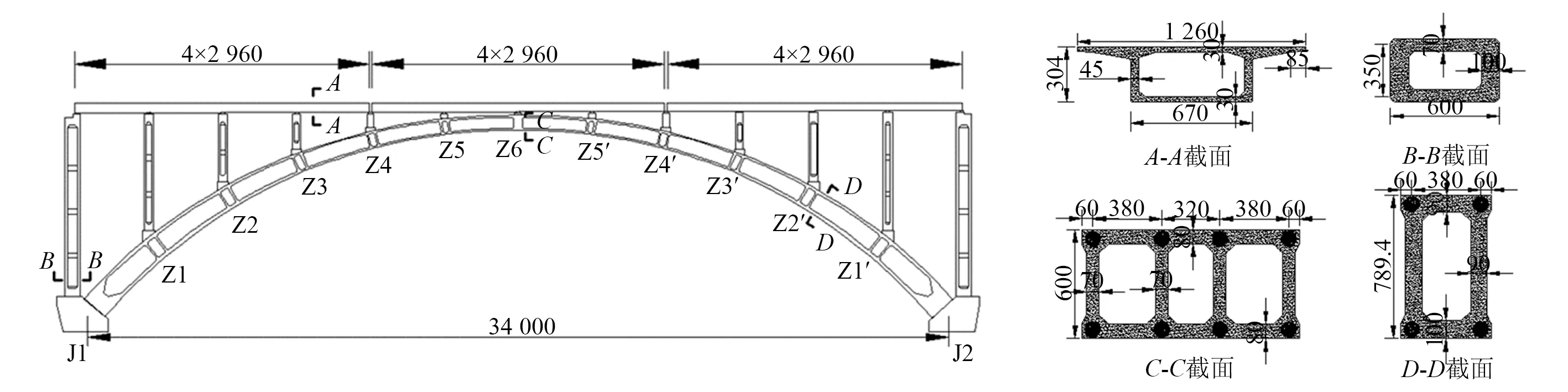
图1 某高速铁路钢管混凝土劲性骨架拱桥结构图(cm)Fig.1 Structural diagram of a high-speed railway CFST stiff-skeleton concrete arch bridge (cm)

1.2 拱桥非线性数值模型

借助OpenSEES平台建立拱桥的非线性数值模型。拱上主梁、拱脚基础在地震下基本处于弹性状态,采用弹性梁柱单元模拟;交界墩、拱上立柱和拱圈劲性骨架(钢管混凝土、联结杆件)均采用基于柔度的非线性纤维梁柱单元(dispBeamColumn element)模拟;基于共节点单元法模拟钢管与内填混凝土的共同作用;拱肋外包混凝土采用考虑剪切的ShellMITC4单元模拟。二期恒载共计147.25 kN/m,作为质量施加在主梁节点上。为考虑材料非线性,分别采用Concrete01和Steel02本构模型模拟混凝土材料与钢材。考虑钢管的约束作用,钢管内填混凝土采用Saenz本构模型[14]。桩-土相互作用与支座采用零长单元(zeroLength element)模拟,本构关系采用相应的理想弹塑性模型。采用刚臂连接模拟拱肋与拱上立柱、拱上立柱与主梁之间的刚性连接,桩基础底部均为全固结。

对于无砟轨道结构,采用弹性梁柱单元模拟底座板、轨道板和钢轨,采用零长单元模拟滑动层、CA层和钢轨扣件,其中轨道结构的本构参数按照有关规范确定[15-16]。钢轨向两侧路基延长100 m以模拟轨道的边界条件,轨道结构如图2所示。全桥施加5%的瑞利阻尼,共计14 471个节点,19 127个单元。基于OpenSEES建立的拱桥非线性数值模型如图3所示。

图2 双线无砟轨道结构示意图Fig.2 Diagram of double ballastless track structure

图3 基于OpenSEES的劲性骨架拱桥数值模型Fig.3 Numerical model of stiff-skeleton concrete arch bridge based on OpenSEES

为验证所建立OpenSEES 数值模型的准确性与有效性,本文采用Midas/Civil软件同步建立了拱桥的有限元模型。OpenSEES模型与Midas/Civil模型的拱桥前5阶自振频率对比如表1所示。注意到第4、第5阶振型中交界墩与拱上立柱纵向弯曲振动明显,应重点关注其地震损伤可能。同时,选取EI-centro地震波将地面峰值加速度(peak ground acceleration, PGA)依次调幅至0.5g,1.0g,1.5g后输入两种模型对比不同烈度地震作用下L/12,L/4,L/2位置处拱肋的位移响应,结果如图4所示。可见,自振频率及拱肋位移响应的最大误差均在10%以内,较好地证明了OpenSEES数值模型的可靠性,可用于拱桥的非线性动力时程分析。

表1 前5阶自振频率对比Tab.1 Comparison of the first 5 order natural frequencies

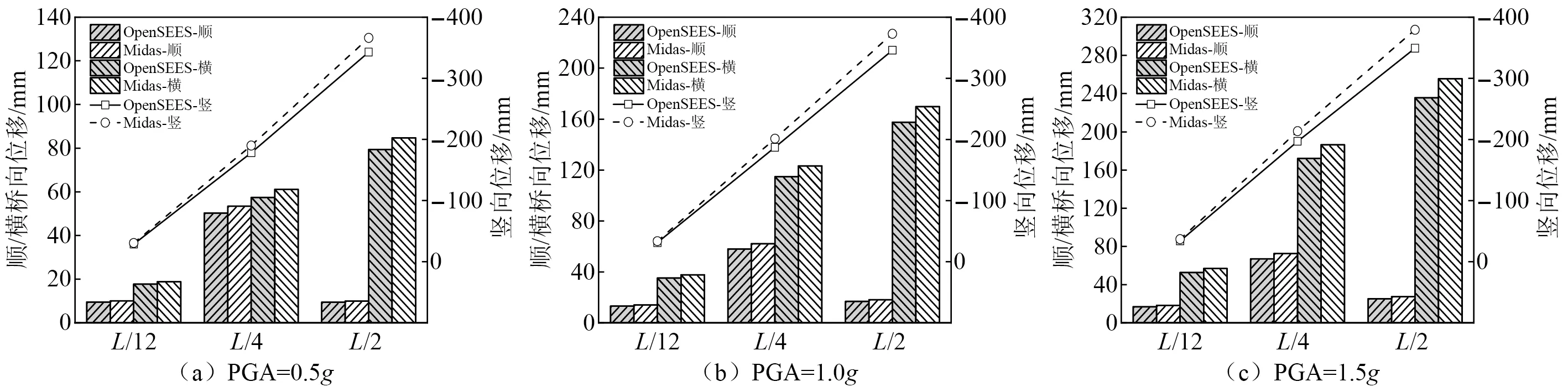
图4 三种烈度地震作用下拱肋位移响应对比Fig.4 Comparison of displacement response of arch rib under three kinds of earthquake intensity

2 地震易损性分析方法

2.1 基于PSDA的地震易损性

结构的地震易损性,是指结构在承受不同强度的地震作用下,发生不同程度破坏的可能性,或者是结构达到或超过某一极限状态(性能水平)的超越概率。由此定义,结构在某一强度地震作用下的失效概率Pf为

Pf=P(D≥C|IM)

(1)

式中:D为地震中结构需求;C为结构能力;IM为地震动强度指标。

假设桥梁在地震作用下的结构需求和结构能力均服从对数正态分布[17]。因此,式(1)中的条件概率可以用标准正态分布函数来定义

(2)

式中:SD和SC分别为以IM为条件的结构地震需求的中位数和结构抗震能力的中位数;βC和βD|IM分别为结构抗震能力和结构地震需求的对数标准差,分别反映了抗震能力和地震需求的不确定性;Φ(·)为标准正态分布函数。

Allin Cornell等[18]认为结构地震需求的中位数SD与地震动强度参数IM的近似关系为

SD=aIMb

(3)

式中,a和b为线性回归分析的系数。

对式(3)两边同取对数变换可得

ln(SD)=ln(a)+bln(IM)

(4)

将式(4)代入式(2),桥梁结构的地震失效概率Pf可进一步表示为

(5)

2.2 基于Copula函数的主拱肋构件系统易损性模型

钢管混凝土与骨架外包混凝土作为两种子构件共同组成劲性骨架拱桥的主拱结构,若仅采用任一子构件的损伤概率对主拱肋进行损伤评价将低估其地震易损性。为准确模拟子构件地震需求之间的相关性,本文引入可以准确描述多个变量相关性的Copula函数方法对构件系统的易损性进行分析[20],以此探究主拱肋的地震损伤概率。

2.2.1 串联构件系统失效概率模型

对于主拱肋,钢管混凝土与骨架外包混凝土均为主要受力构件,其中任一子构件的失效均会影响拱桥的正常使用。因此采用由子构件组成的串联模型模拟主拱肋构件系统,模型示意图如图5所示。

图5 基于串联模型的主拱肋构件系统示意图Fig.5 Schematic diagram of the main arch system based on the tandem model

基于串联构件系统模型,可得钢管混凝土系统与骨架外包混凝土系统的损伤概率为

(6)

式中:PSC为钢管混凝土系统的损伤概率;PSCi为单个钢管混凝土的损伤概率;POC为骨架外包混凝土系统的损伤概率;POCi为单侧外包混凝土的损伤概率;m为拱肋截面内钢管混凝土的个数;n为拱肋截面外包混凝土的面数。

同理可得主拱肋构件系统地震损伤概率PA的表达式为

(7)

2.2.2 Copula函数

假定Copula函数中的n元随机变量为X=(X1,X2, …,Xn),F为n元联合概率分布函数,F1,F2,Fn分别为各个变量的边缘分布函数,则存在Copula函数C对于任意x=(x1,x2, …,xn)∈Rn有[21]

F(x1,x2, …,xn) =
C[F1(x1),F2(x2), …,Fn(xn)]

(8)

(9)

由式(8)、式(9)可知,Copula函数考虑了变量之间的相关性,将多元变量的联合概率分布函数与各变量的边缘概率分布函数联系起来。基于Copula函数的多元随机变量联合概率密度函数为

(10)

式中:c[·]为Copula函数的密度函数;fi(xi)为随机变量xi的边缘概率密度函数。

基于AIC准则,本文选取两种常见的阿基米德Copula函数:Gumbel Copula函数和Clayton Copula函数对主拱肋构件系统内子构件地震需求之间的相关性进行描述[22],二者的函数表达式分别为

CG(u1,u2;α)=
exp[-{(-lnu1)α+(-lnu2)α}1/α]

(11)

(12)

式中:u1,u2分别为随机变量x1,x2的边缘分布函数;α,β为随机变量x1,x2之间的相关参数,可由随机变量之间的Kendall秩相关系数τ计算得出

(13)

(14)

2.2.3 基于Copula函数的串联构件系统失效概率模型

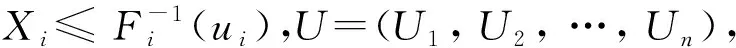
(15)

基于上述二元Copula函数,考虑串联构件系统内子构件失效模式同时发生的概率为

P[l1(X1)≤0,l2(X2)≤0]=
P[L1(l1(X1))≤L1(0),L2(l2(X2))≤L2(0)]=
P[U1≤L1(0),U2≤L2(0)]=
C[L1(0),L2(0)]=C[P1,P2]

(16)

式中:l1和l2为基于串联体系的二元子构件失效模式功能函数;P1和P2为单个子构件的损伤概率。

基于式(16),对式(6)、式(7)进行求解得到串联构件系统损伤概率的计算公式分别为

PSCi=PSi+PCi-C(PSi,PCi), 1≤i≤m

(17)

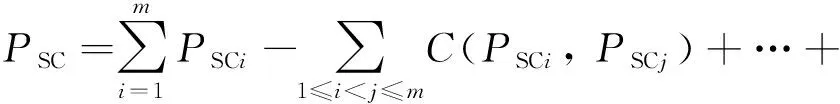
(18)

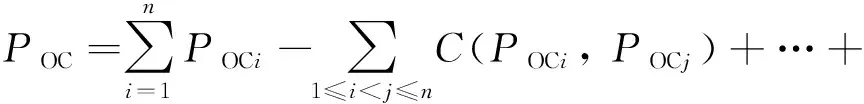
(19)

PA=PSC+POC-C(PSC,POC)

(20)

式中:PSi为单个钢管的损伤概率;PCi为单个钢管内填混凝土的损伤概率;C(…)为多个子构件同时发生破坏的损伤概率。

2.3 构件损伤指标

定义桥梁构件的损伤指标是进行易损性分析的重要前置步骤,目前常用的指标有桥墩曲率、曲率延性比、位移、应变、应变延性比等。其中应变指标可用于多维度地震作用下构件的损伤判别,因此本文采用应变指标对钢管混凝土构件与钢筋混凝土构件的损伤等级进行评价[24]。对于外包混凝土,借鉴高层建筑层间位移角指标[25],选用壳单元相对位移角作为损伤指标。相对位移角定义为

(21)

式中:i,j为顺桥向外包混凝土壳单元节点编号;x,y,z分别为节点在顺桥向、横桥向与竖向的位移;l为外包混凝土单元长度。

根据不同的损伤指标,将桥梁构件的损伤状态划分为:无损伤(ND)、轻微损伤(SD)、中等损伤(MD)、严重损伤(ED)以及完全破坏(CD)共5个损伤等级。劲性骨架拱桥的损伤等级划分与构件损伤指标如表2所示,具体数值的选取参考Wei等、周长东等和吕西林等的研究。

表2 劲性骨架拱桥损伤等级划分与构件损伤指标Tab.2 Damage classification of stiff-skeleton concrete arch bridge and components damage index

2.4 地震动的选择及输入

从太平洋地震工程中心NGA-West2数据库中选取与桥址场地条件相近的25组地震动记录,相应的加速度反应谱如图6所示。

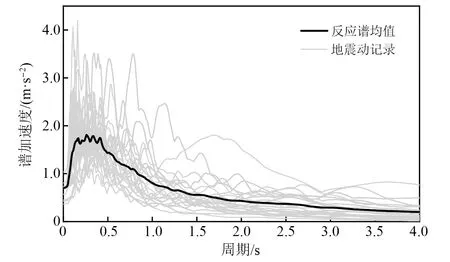
图6 所选25组地震动记录加速度反应谱Fig.6 Selected 25 sets of ground vibration recorded acceleration response spectra

每组记录均包含顺桥向X、横桥向Y与竖向Z的地震动。为满足概率统计分析的要求,采用IDA将25组地震动的峰值加速度以0.1g为步长依次从0.1g调幅至1.5g,共生成375组地震动。将其沿顺桥向、横桥向与竖向输入结构,分析劲性骨架拱桥在三向地震动同时作用下的损伤情况。

3 劲性骨架拱桥地震易损性分析

3.1 控制构件的确定

劲性骨架拱桥的构件种类繁杂且数量众多,为减少时间成本,很有必要选取代表性强、重要性系数高的控制构件进行易损性分析。根据文献整理,在以往同类型拱桥的震害中,主要有三种易损构件系统:主拱肋、交界墩与拱上立柱。为确定三种构件系统的控制截面位置,本文选取一条与场地条件相近的地震波进行结构试算,根据结构位移响应确定控制截面。试算地震波三向加速度时程曲线与拱肋节点位移,如图7所示。

由图7可知,三向地震动作用下劲性骨架拱桥的上、下弦拱肋在L/12,L/4和跨中位置处出现位移极值。同时综合考虑主弦钢管混凝土内力的分布情况[26],本文选取的控制构件如表3所示。

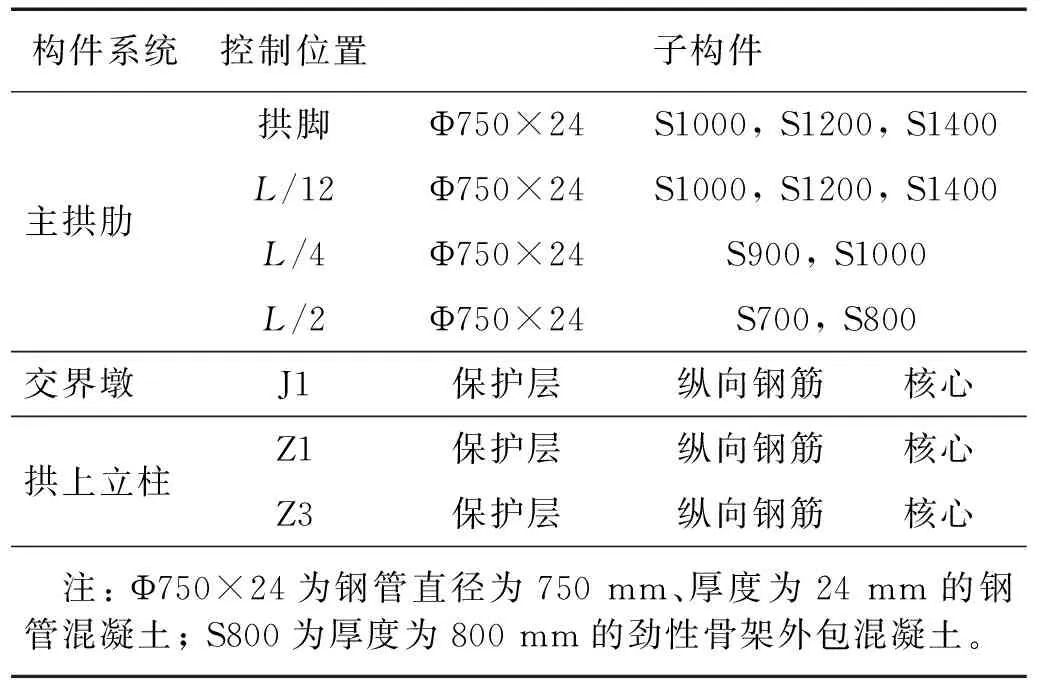
表3 三向地震动作用下劲性骨架拱桥控制构件Tab.3 Control elements for stiff-skeleton concrete arch bridge under three-way ground shaking

3.2 主拱肋易损性曲线

3.2.1 主拱肋系统子构件易损性曲线

限于篇幅,仅将由Clayton Copula函数计算出的每个控制截面内最易损子构件的损伤概率列出,如图8所示。

图8 主拱肋系统子构件地震易损性曲线Fig.8 Seismic vulnerability curves of subcomponents of the main arch system

由图8可知,在四种破坏状态下,控制截面的外包混凝土(OC)的损伤概率明显大于钢管混凝土(SC)。表明地震动作用时,外包混凝土的相对位移角超限而成为易损结构,主拱肋的相对位移变形将对高速列车的行车安全造成潜在隐患,在后续抗震设计时应注意相应位置相对位移变形的控制。主拱肋内填混凝土由于钢管的约束与套箍作用,强度得到较大提高,压应变超限概率较低,表明在强震作用下抗震性能较好,钢管内填混凝土大概率处于弹性工作状态,个别可能会出现轻微损伤;钢管混凝土的最大轻微损伤概率为52.1%～66.3%,中等损伤概率为10.0%～17.8%。整体来看,相比于钢管混凝土,外包混凝土的相对变形损伤概率与损伤程度均更为严重。

对比不同控制截面的易损性发现,对于外包混凝土,L/4拱肋截面 (Z3-OC)的损伤概率最大,其次为L/12(Z1)、跨中(Z6)与拱脚截面(J1);对于钢管混凝土,当PGA<0.9g时,L/4与跨中截面的钢管混凝土损伤概率相较于L/12与拱脚截面更小,然而随着地震动强度的增大,前两者的损伤概率大于后两者且呈现正增长趋势,表明钢管混凝土的易损截面位置将随着PGA的增大而发生改变。应特别注意强震作用下拱脚钢管混凝土应变超限而出现中等损伤甚至严重损伤的可能。

3.2.2 主拱肋构件系统易损性曲线

通过引入Copula函数将钢管混凝土与外包混凝土的易损性相结合,共同构建主拱肋系统的易损性。4个控制截面的易损性曲线如图9所示。

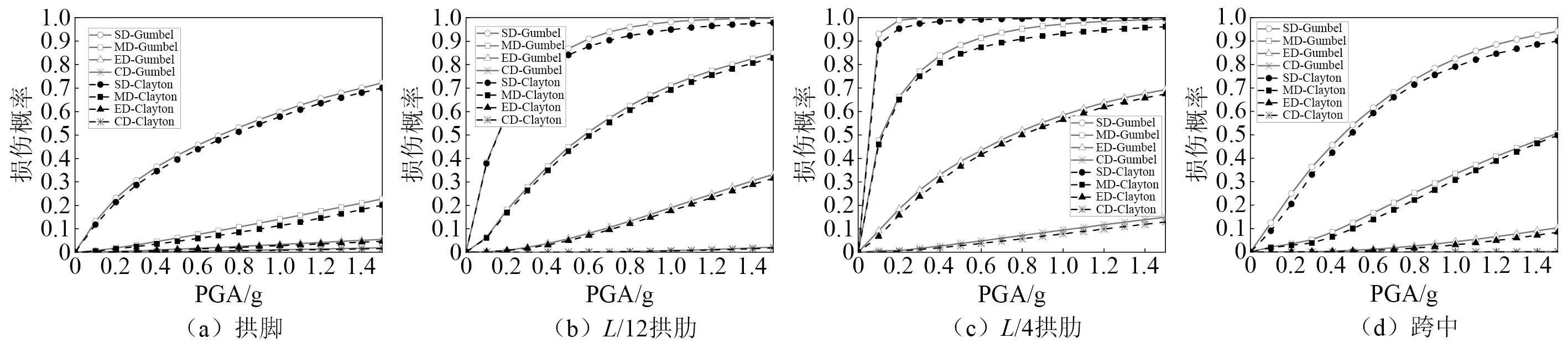
图9 主拱肋构件系统地震易损性曲线Fig.9 Seismic fragility curves of the main arch system

由图9可知, 由Gumbel函数与Clayton函数建立的主拱肋系统易损性曲线基本一致,对比4个控制截面的易损性结果可以发现,两者的最大计算偏差分别为3.0%,3.6%,4.5%,4.7%,前者计算的损伤概率略大于后者,即对于主拱肋系统的易损性Gumbel函数更偏于保守。总结4个拱肋截面的易损性规律发现,当PGA<0.4g时,轻微损伤和中等损伤的增长速度较快,表明此时拱肋轻微和中等损伤的发展十分迅速,对地震动强度的变化较为敏感;当PGA>1.0g时,除拱脚截面外其余拱肋控制截面轻微损伤的超越概率均基本达到85%以上,即此时主拱已达到轻微损伤标准。相比于前两种损伤状态,严重损伤与完全破坏的增长速率较为平缓。整体来看,主拱结构在同一地震动强度作用下,完全破坏的超越概率要远小于前三种损伤概率,说明主拱具有较强的安全储备,地震动作用下发生完全损伤破坏的概率较小。对比不同控制截面的易损性可以发现,四种损伤状态下L/4拱肋均为最易损位置,原因为此处的外包混凝土相对位移角指标最大,在抗震设计时应重点考虑对此处进行变形控制。

3.2.3 Copula函数系统易损性与子构件及第一可靠度原理易损性的对比

为了验证基于Copula函数的主拱肋系统易损性的合理性与准确性,将其分别与子构件易损性及基于第一可靠度原理的系统易损性进行对比分析。

基于第一可靠度原理,串联系统易损性下界由假定子构件地震响应之间完全相关确定,上界由假定子构件地震响应之间完全不相关确定[27]。通过上、下界限确定的系统易损性为

(22)

式中:P(Fi)为各子构件达到损伤状态的概率值;P(Fsys)为串联系统达到损伤状态的概率值。

以L/12主拱肋截面为例,将两种Copula函数计算得到的系统易损性与该截面内最易损子构件的易损性及基于第一可靠度原理的系统易损性共同绘制于图10。

图10 Copula函数系统与子构件及上、下界的易损性对比Fig.10 Comparison of the seismic fragility curves for subcomponents, upper and lower bounds and Copula function systems

对比Copula主拱肋系统与子构件的易损性曲线可以发现,在四种破坏状态下,系统的易损性大于任一单个子构件的易损性,因此以任一子构件的易损性考虑主拱肋系统的易损性,都将低估其损伤概率。同时发现,主拱系统的易损性曲线更靠近于外包混凝土,这是由于钢管混凝土的损伤概率较小,而串联系统的易损性由损伤概率最大的子构件控制。随着地震动强度的增加,构件系统与子构件易损性之间的差别逐渐增大,在轻微损伤情况下差别尤为明显。因此,在强震作用下采用子构件的损伤概率代替考虑主拱肋系统的概率将低估其易损性。

对比Copula主拱肋系统与基于第一可靠度原理的系统易损性曲线可以发现,通过两种Copula函数得到的易损性曲线均位于一阶界限法的上、下界之间,且偏向于下界。由Copula函数得到的主拱肋系统易损性与下界的最大偏差分别为3.7%,9.0%,7.3%,0.7%,表明假定子构件地震响应之间完全相关会略微低估主拱肋的易损性;由Copula函数得到的主拱肋系统易损性与上界的最大偏差分别为-45.5%,-43.9%,-40.9%,-3.6%,表明假定子构件地震响应之间完全不相关会显著高估主拱肋的易损性,即以上界分析其发生轻微损伤、中等损伤及严重损伤的概率将过于保守。

3.3 交界墩与拱上立柱易损性曲线

地震发生时,拱桥墩柱在拱上主梁地震惯性力的作用下,相对于主拱肋产生较大位移,二者彼此间变形不协调而在固结处产生附加内力。鉴于此,本文选取与拱肋固结位置处的墩柱截面进行易损性分析,相应的易损性曲线如图11(a)～ 图11(c)所示。

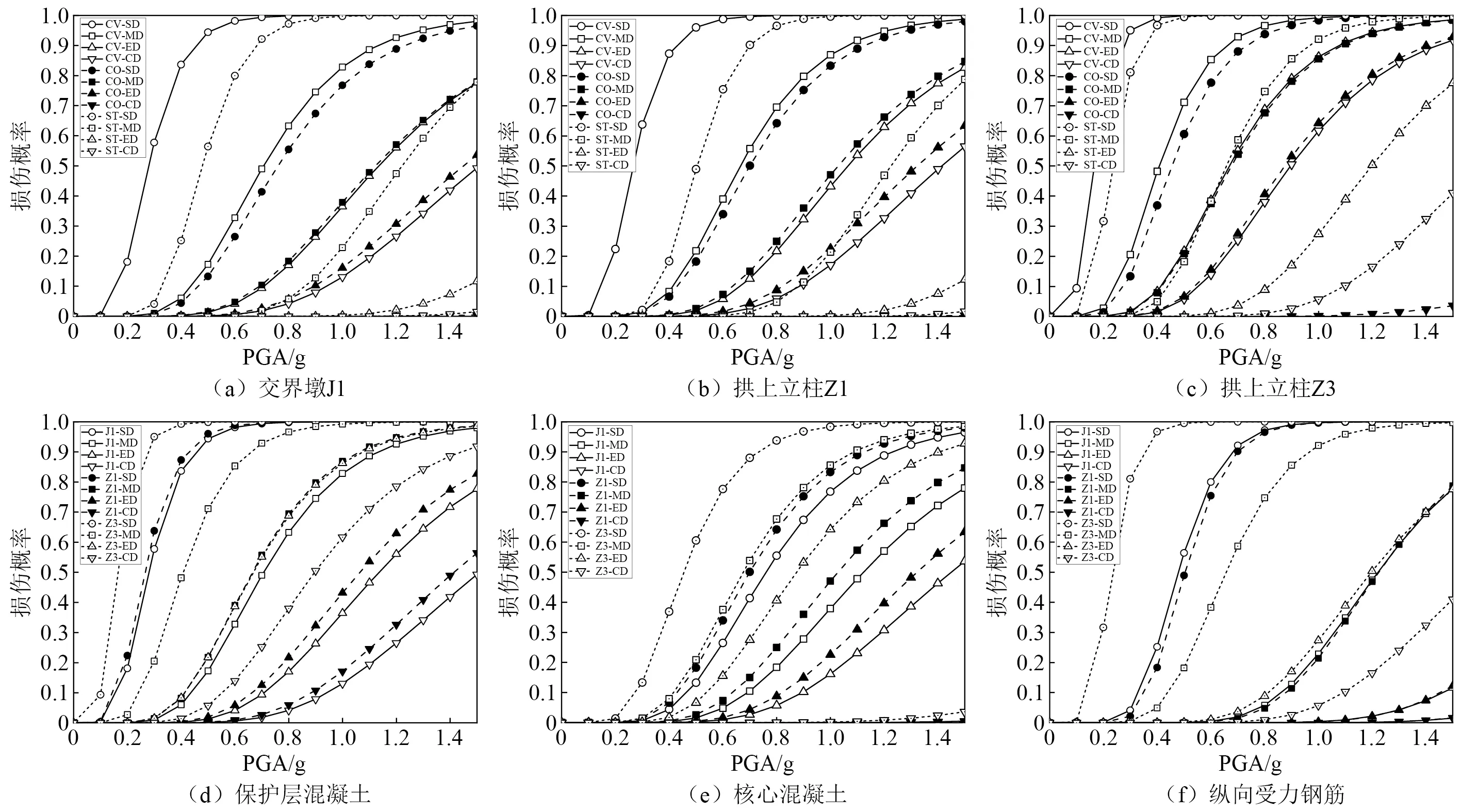
图11 交界墩与拱上立柱地震易损性曲线Fig.11 Seismic fragility curves of the crossing pier and column on arch

由图可知: 3个控制墩柱在四种损伤状态下,保护层混凝土(CV)的易损性水平均明显高于纵向钢筋(ST)和核心混凝土(CO),即墩柱的保护层混凝土在三向地震动作用下更易发生损伤。相比于纵向钢筋,核心混凝土发生轻微损伤的概率较小,但随着PGA的增加其严重损伤的概率相较于纵向钢筋迅速增大,即发生严重损伤的概率更大。分析其原因为,钢筋混凝土构件在地震波能量较低时主要由延性较好的钢筋通过拉压变形消散地震能量,随着地震动强度的增大,钢筋达到屈服应变 (轻微损伤)后,混凝土承受更多地震荷载,在达到极限压应变0.2%后(轻微损伤)快速发展为深层次损伤,此时中等与严重损伤概率会大幅增加。值得注意的是,Z3纵向钢筋在PGA=1.0g时完全破坏的概率迅速增加,表明已经发生了严重的塑性损伤,这与J1,Z1的破坏情况是不同的。

为了基于材料层面对比不同位置处墩柱损伤情况的差异,依次将J1,Z1,Z3的保护层混凝土、核心混凝土及纵向受力钢筋的易损性曲线依次绘制如图11(d)～图11(f)所示。由图11可知,Z3三种构件的四种损伤状态概率均显著高于J1,Z1,其中纵向钢筋的损伤概率相差最大,四种损伤概率的最大差值分别为78.9%,74.2%,65.3%和39.4%。J1与Z1的构件损伤情况则较为接近,后者略大于前者。总体来看,位于L/4拱肋处的立柱Z3损伤概率与损伤程度最大,这与唐堂等[28]的研究结论相一致。因此在后续进行劲性骨架拱桥的减震设计研究时,应重点考虑对L/4拱肋的拱上立柱采取加强的设防措施。

4 结 论

(1) 本文基于OpenSEES平台建立了一座上承式钢管混凝土劲性骨架拱桥的非线性动力时程分析数值模型,并通过与Midas Civil模型的自振频率及主拱位移响应进行对比,验证了数值模型的合理性与可靠性。

(2) 三向地震动作用下,主拱肋外包混凝土的损伤概率与损伤程度均明显大于钢管混凝土,在后续抗震设计时应注意对L/4主拱肋截面相对位移角的控制;主弦钢管混凝土的易损位置将随着PGA的增大而发生从跨中向拱脚的改变。

(3) Copula函数主拱肋系统的易损性大于任一单个子构件的易损性,且偏向于外包混凝土,L/4拱肋截面的损伤概率最大;通过两种Copula函数得到的系统易损性曲线均位于一阶界限法的上、下界之间,且偏向于下界,Gumbel Copula函数更偏于保守;假定子构件地震响应之间完全相关和完全不相关将分别略微低估和显著高估主拱肋系统的易损性。

(4) 交界墩与拱上立柱的保护层混凝土的易损性水平显著高于纵向钢筋和核心混凝土;相比于纵向钢筋,核心混凝土发生轻微损伤的概率较小,但其发生严重损伤的概率更大;位于L/4拱肋位置的立柱损伤概率与损伤程度最大,抗震设计时应重点考虑对其采取加强的设防措施。