运输包装随机振动的加速度响应谱分析

杨松平, 王志伟

(1. 暨南大学 包装工程学院 包装工程研究所,广东 珠海 519070;2. 暨南大学 力学与建筑工程学院 重大工程灾害与控制教育部重点实验室,广州 510632;3. 暨南大学 产品包装与物流广东普通高校重点实验室,广东 珠海 519070)

运输包装件在物流过程中遭受外界振动作用发生损伤或失效[1],为评估产品运输包装的有效和适度性,数学建模和理论分析成为了必要手段。通常将运输包装件模型化为单自由度质量-弹簧-阻尼模型,为预测产品主体响应,包装优化设计提供了理论依据[2]。然而,产品关键部件与主体连接的叠加结构,会激发关键件比产品主体更大的响应。另外,产品主体有较大的脆值,而产品内部关键部件的脆值相对较小,关键件功能往往先受到破坏,以至于产品失效。为了合理优化包装设计,需要分析外界激励、产品主体和关键件相互作用机理,重点评价产品关键件的安全程度。

由于很大一部分包装材料在一定变形范围内符合正切型本构关系,通常用两自由度正切型的质量-弹簧-阻尼模型来表征运输包装件[3],该系统的破损边界理论研究取得了很好的进展[4]。Wang等[5-9]研究了该系统在脉冲激励下的破损边界曲面(曲线),重点讨论系统参数(阻尼比、频率比、质量比)对于破损边界的影响。卢富德等[10-11]建立了正切型两自由度包装系统在矩形加速度脉冲激励下的冲击响应谱曲面及破损边界曲面。郭蓓蓓等[12]、霍银磊等[13]分别采用同伦法、摄动法得到了正切型非线性包装系统跌落冲击响应的近似解析解,上述方法也可用来解决高维非线性包装系统的冲击响应问题[14]。以往研究主要集中在正切型非线性包装系统冲击破损边界理论方面。

在包装随机振动领域,金潇明[15]分析了随机振动激励下考虑易损件的两自由度产品包装系统的动力学响应,基于线性累积理论分析了易损件疲劳损伤概率。汤伯森等[16]研究了两自由度线性包装系统在振动脉冲激励下的产品易损件的加速度响应均方差等统计参数,分析了振动环境因素对于系统响应的影响。Rouillard[17]研究了堆叠包装单元遭受车辆垂直振动下的动态行为,介绍了一种用于预测堆叠式包装系统动态响应的数值模型。徐伟民等[18-19]建立了路面加速度、位移和脉冲联合激励下车辆-运输包装件耦合多自由度系统模型,获取了产品加速度响应数值解。李晓刚[20]构建了白噪声激励下多自由度车辆包装件耦合系统,给出了易损件及产品响应时域和频域数值功率谱。杜恒[21]进行了随机激励下堆码包装系统的仿真分析,获得系统的加速度响应。王志伟等[22]建立堆码包装试验模型,试验研究了系统的加速度响应及包装容器间动压响应,发现加速度响应的峰值分布及动压力的力水平穿越分布均接近韦伯分布,并分析了包装件跳起对于响应的影响。朱大鹏[23]在考虑了真实随机振动激励的功率谱特征基础上提出了包装件失效概率分析方法,并以三次非线性包装件为例数值分析了关键部件在随机振动激励下首次穿越损坏概率。上述研究主要通过数值和实际试验来获取含关键件的非线性包装件的加速度响应谱,而且以往研究主要集中在正切型包装系统冲击破损边界理论,正切型包装系统随机振动研究几乎空白,而且尚未建立非线性包装系统加速度响应谱理论,然而产品的加速度响应是评价产品包装有效性的关键指标。因此,本文将探索两自由度运输包装正切型系统的加速度响应谱相关理论,尝试建立系统的加速度响应谱理论,并指出所提理论的适用范围,同时采用数值模拟的方法验证了理论的有效性,并进一步分析了加速度响应谱对于系统参数的敏感性,探析系统的非线性效应。文中方法不仅能够有效的预测产品主体和关键件的响应,也为包装防护优化设计提供理论依据。

1 考虑关键部件的运输包装件动力学模型

考虑关键部件的运输包装件以两自由度非线性刚度的质量-弹簧-阻尼模型来描述,如图1所示。

图1中:mp和m1分别为产品主体和关键件的质量;F(δ)和cp分别为缓冲包装材料的非线性恢复力和阻尼;k1和c1分别为关键件与产品主体连接部的等效刚度和阻尼;y为外部位移随机激励;xp为产品主体的位移响应;x1为产品关键部分的位移响应。

许多缓冲包装材料的非线性恢复力F(δ)与变形δ关系遵循正切型力-位移关系,如图2所示。可通过式(2)进行描述

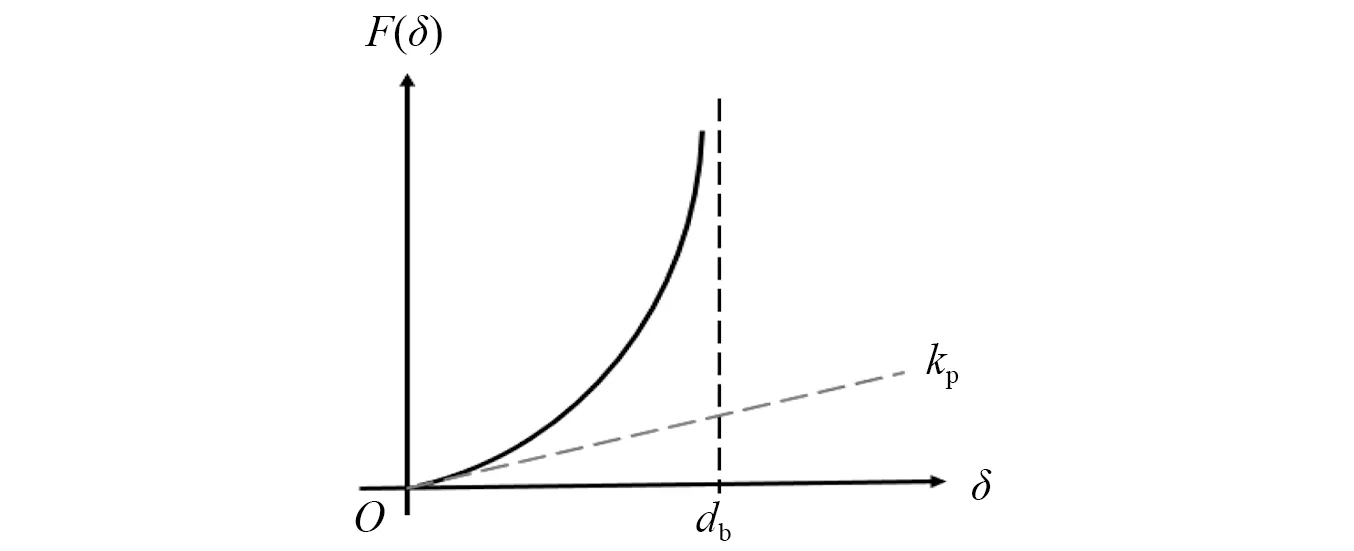
图2 正切型缓冲材料力-位移关系Fig.2 Force-displacement relationship of tangential packaging material

(1)

式中:kp为正切型缓冲材料的初始线弹性系数;db为正切型材料的变形极限。

缓冲系统的恢复力F(δ) 考虑为正切型非线性恢复力,材料的阻尼假设为线性的,将关键件的连接部分作线性化假设,即k1和c1视为线性刚度和线性阻尼。因此,可以建立考虑关键件的运输包装系统的动力学方程

(2)

令xp-y=δp,x1-xp=δ1,则有

(3)

在此基础上,可进一步写出考虑关键件的正切型运输包装系统相对位移形式的动力学方程

(4)

产品主体及关键件的加速度响应是重点,可以通过式(5)进行求解

(5)

2 考虑关键部件的运输包装系统加速度响应谱理论

由于非线性因素,暂无法求解该类系统的精确平稳解[24]。为了求解两自由度正切型包装系统的加速度响应近似解析解,需引入等效线性化方法[25]先对原始系统动力学方程作处理,然后再利用累积量截断法[26]求解等效线性系统的相对加速度响应近似解析解,再通过相对加速度与绝对加速度关系式,得到产品主体及关键件的加速度响应谱近似解析解。同时,等效线性系统的刚度系数也可以通过该方法给出。为了验证所提方法的正确性,进行了考虑关键件的两自由度正切型产品包装系统的加速度响应谱数值模拟,结果与理论推导进行了对比,讨论了方法适用的工程条件及范围。

2.1 系统加速度响应谱理论

关键件-产品两自由度正切型包装系统的加速度响应理论谱可通过以下步骤建立:

步骤1系统的动力学方程式(4)用以下等效线性系统进行替换

(6)

式中,ae为等效刚度系数,根据等效系统与原始系统差最小原理,可得

(7)

结合正切函数的泰勒展示式

(8)

由式(7)和式(8)可得

(9)

式中,m4000和m2000分别为四阶和二阶累积量,忽略四阶以上的累积量,即高于四阶累积量为0。

(10)

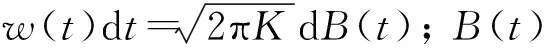
(11)

利用Mathematica工具,可求解上述方程中的各阶矩,具体步骤如下:

首先,从上述方程组提取出统计矩的矩前系数,组成Q矩阵,用方程组中的常量组成F矩阵;其次,将提取好的Q矩阵以及O矩阵按照矩阵格式输入软件中,其中所有变量均用符号进行表示。引用Inverse[Q]命令直接输出Q的逆矩阵Q-1;由于无法直接通过命令Dot[-Q-1,F]得出点积的结果,所以通过观察F矩阵的结构,将Q-1在运算过程中与F中非零项相关的列向量单独提取出来,与F中非零项的相反数单独相乘,得到与-Q-1×F相同的运算结果。由此可得到所有统计矩的符号表达式,参数具体赋值便可得到各阶矩。

注意到m1100=m0011=0。因为等效线性化参数ae与二阶m2000和四阶矩m4000有关,考虑二阶以上截断方法时,需用迭代方法确定等效线性化参数。

步骤4在Ito方程式(11)两边同时乘以X1(t)和X3(t),并作集合平均,则有

(12)

(13)

式中,Rij(τ)为相关函数,Rij(τ)=E[Xi(t)Xj(t-τ)]。

步骤5根据积分变换规则,转变为频域方程

(14)

(15)

求解上述方程,可得

(16)

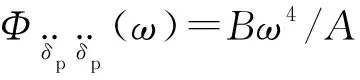
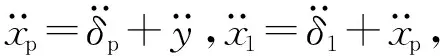
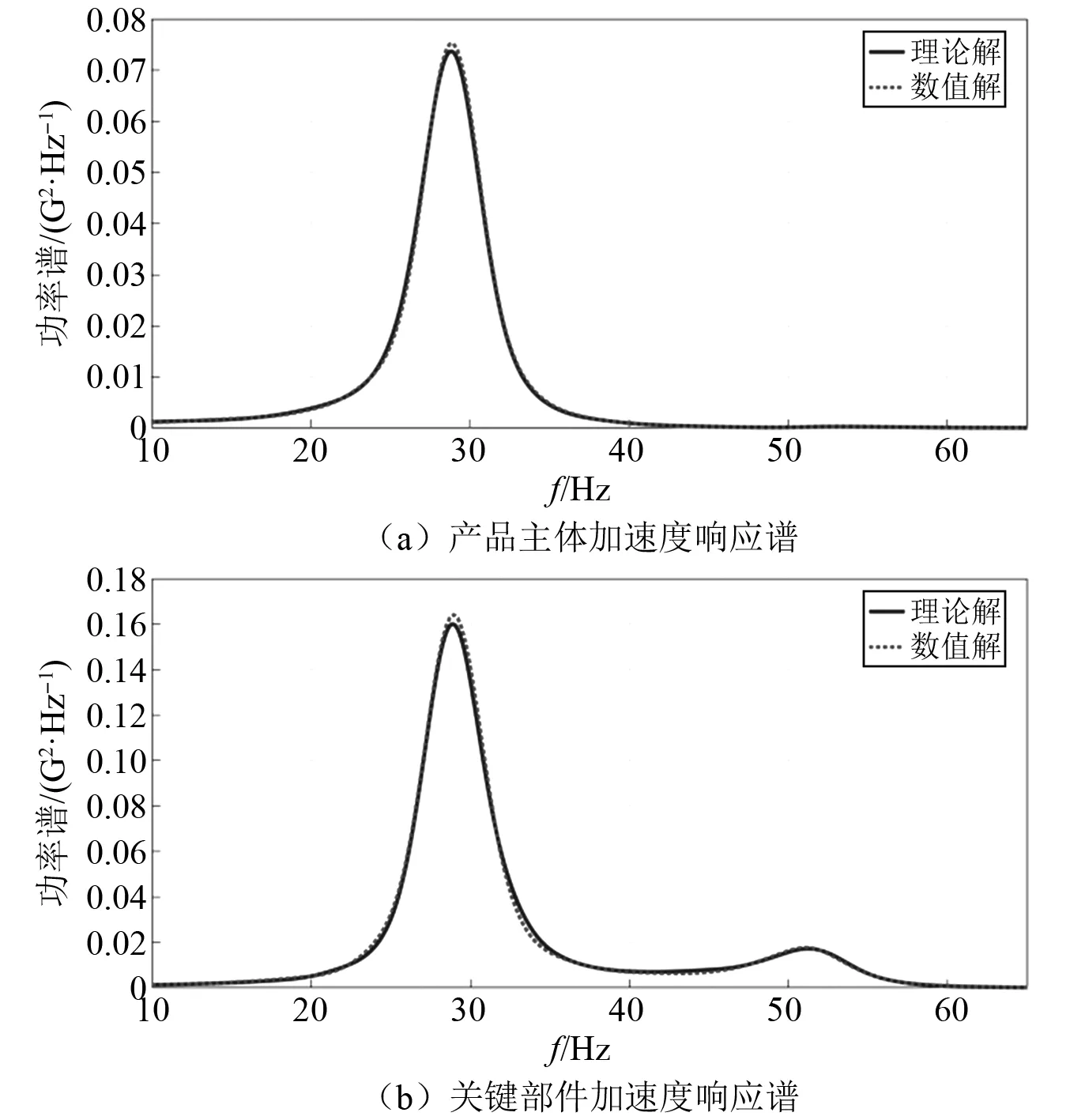
图3 正切型系统的加速度响应理论谱与数值解比较Fig.3 Compare of theoretical and numerical acceleration response spectrum for tangent system

正切型系统关键件及产品主体的响应加速度理论谱与数值模拟结果匹配较好,验证了方法有效性。产品主体主要受一阶共振频率控制,二阶共振处峰值较小,关键件的加速度响应表现为由一阶、二阶共振频率控制,产品主体的加速度响应明显小于产品关键件的响应。

2.2 系统加速度响应谱理论适用范围

3 系统加速度响应谱参数研究

为了进一步研究系统参数和外界激励对于加速度非线性响应的规律,通过数值模拟的方式给出了在不同参数和激励水平条件下考虑关键件的正切型包装系统的加速度响应数值谱。

3.1 不同激励水平对于加速度响应谱的影响

为了考察外界激励水平对于两自由度正切型包装系统的加速度响应影响。首先,假设产品关键件对产品的质量比a1为1/20,关键件与产品主体的连接部具有与缓冲材料相同阻尼比0.05,且连接系统频率参数为ω1=50,而缓冲系统初始频率参数ωp=30,特征参数β=30。图4给出了5个激励等级下(K=0.001 g2/Hz,K=0.004 g2/Hz,K=0.008 g2/Hz,K=0.010 g2/Hz,K=0.020 g2/Hz)产品主体与关键件的加速度响应谱。

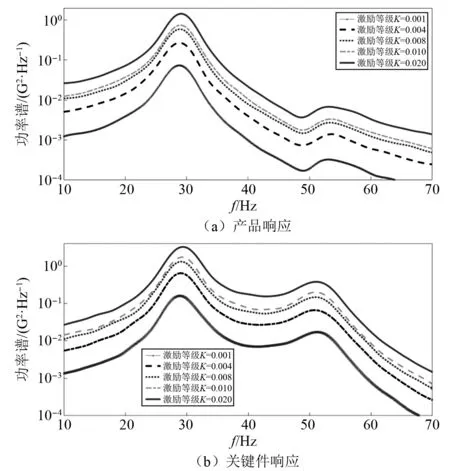
图4 不同激励水平下正切型系统加速度响应数值结果Fig.4 Numerical acceleration responses of the tangent system under different excitation levels

图4展示了不同激励水平下产品主体及关键件加速度响应数值结果。从图4可以看出,产品主体及关键件加速度响应均随着激励水平的提高而逐渐增大,同一激励等级下,关键件加速度响应明显高于产品主体的响应,被一阶、二阶共振频率控制,而产品主体加速度响应主要被一阶共振频率影响,一阶共振处响应明显远大于二阶共振处响应。随着激励等级的提高,正切型弹簧的“硬化”非线性作用愈加明显,使得产品主体的一阶响应峰值点频率及关键件一阶、二阶响应峰值点频率向右边偏移逐渐增大,而产品主体二阶响应峰值量级较小,未激发出正切型弹簧的非线性效应,保持较为一致的共振频率。

3.2 非线性特征参数对于加速度响应谱的影响

从式(4)动力学方程可以看出,两自由度线性系统与两自由度正切型非线性系统,主要差别体现在非线性刚度上,假设其具有相同的频率参数ωp,最大的差异便是正切型弹簧具有非线性特征参数β,锁定激励等级K=0.001 g2/Hz,除了非线性特征参数β,其他参数与上文相同,图5数值模拟探索了不同正切型缓冲材料特征参数(β=3,β=90,β=270)的产品主体及关键件加速度响应谱。

图5 不同缓冲材料非线性特征参数的系统加速度响应数值谱Fig.5 Numerical acceleration response spectrums of system for different cushion material characteristic coefficients

此外,产品关键件响应对于非线性特征参数较为敏感,尤其是二阶共振处峰值及一阶共振频率会随着特征参数出现较为单一规律的敏感变化,而对于一阶共振处峰值影响规律不单一。产品主体的二阶共振响应远小于一阶共振处响应,所以对于产品主体而言,只需关注非线性特征参数对于其产生一阶共振调频作用。

鉴于此,在用正切型缓冲材料包装产品时,要想得到较好的减振效果,需适当选择合理的特征参数β,存在一个最佳的缓冲材料特征参数β*,使得关键件的一阶响应峰值最小。另外,特征参数β通过调节峰值点间频率带宽的作用,也存在一个使关键件加速度响应总体能量最低的最佳值。

3.3 关键件与产品主体质量比对于加速度响应谱的影响

设K=0.001 g2/Hz,ω1=50,ωp=50,ξ1=0.05,ξ2=0.05,β=30,图6描绘了不同质量比a1(1/40, 1/30, 1/20,1/10,1/5)非线性特征参数β=30条件下产品及关键件加速度响应数值结果,质量比对产品及关键件的加速度响应影响显著。在产品主体质量一定的情况下,产品关键件质量的下降使得产品及关键件加速度一阶响应峰值点频率左移变小,却使两者二阶峰值点频率右移变大,起到“调频调节峰值点间频率带宽”作用,能够有效的增加产品主体及其自身响应峰值频率范围。关键件质量的变化影响着产品主体的响应,相当于关键件起到了调谐减震器的作用,对于调谐减震器而言,质量比是减振效果的关键参数,也对敏感频率处(缓冲材料及连接件频率附近)有调节峰值作用[28]。

图6 不同质量比的正切型系统加速度响应数值结果Fig.6 Numerical acceleration responses of tangent system with different mass ratios

3.4 对缓冲系统频率参数及连接系统频率参数敏感性

令K=0.001 g2/Hz,a1=1/20,ω1=50,ξ1=0.05,ξ2=0.05,β=30,图7给出了不同缓冲系统频率参数(ωp=10,ωp=20,ωp=30,ωp=40,ωp=50,ωp=60)对于产品及关键件加速度响应影响的数值分析结果,缓冲系统频率参数对于产品主体及关键件响应频带具有十分明显的调节作用,当其他参数一定的情况下,产品主体一阶响应峰值主要受缓冲系统频率参数控制,当缓冲系统频率参数接近连接件的频率参数时,即频率比接近于1,使得产品主体的响应最小,此时关键件响应最大,该结论与两自由度调谐减振器相同[29]。随着频率参数的升高产品主体的二阶响应峰值逐渐增大。

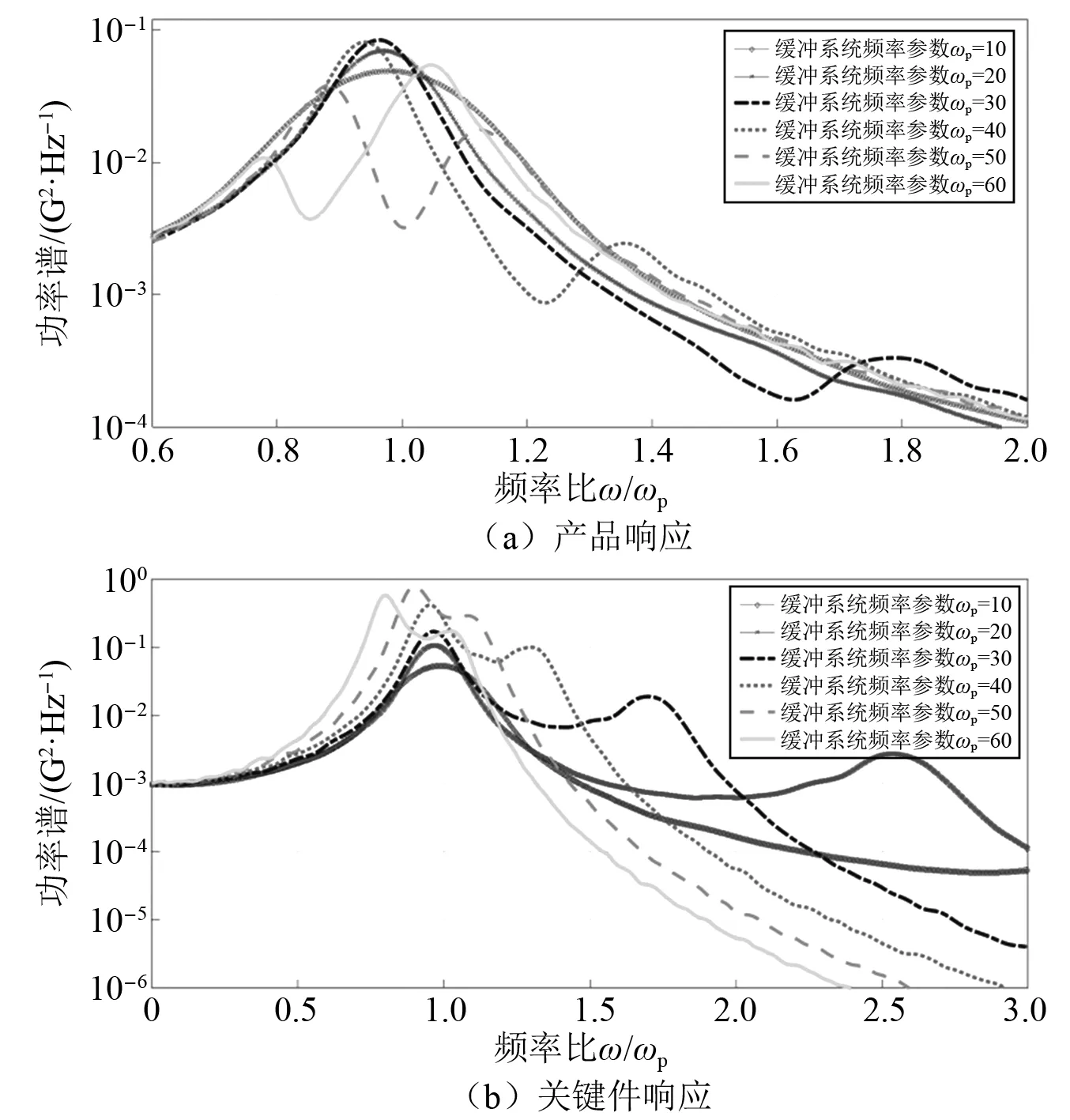
图7 不同缓冲系统频率参数的正切型系统加速度响应数值谱Fig.7 Numerical spectrums of tangent system acceleration response with different cushion system frequency parameters

缓冲系统频率参数对于产品关键件响应峰值点及峰值点频率影响规律较为单一,当其小于连接件频率参数时,随着缓冲系统频率参数的升高产品关键件的一阶、二阶峰值逐渐增大,产品关键件的一阶响应主要受缓冲系统频率参数影响,而二阶响应受连接系统频率参数作用。当大于连接件频率参数,则出现相反的规律。

所以在包装优化设计过程中,适当选择具有相对较小频率参数的缓冲材料,远离连接件的频率参数,对于关键件的保护能起到的作用,而对产品主体影响不大。同时还需兼顾考虑,较小频率参数的缓冲材料也比较“软”,是否对产品达到了固定和支撑作用。

锁定ωp=30,其他参数保持不变,图8给出了不同连接系统频率参数(ω1=30,ω1=40,ω1=50,ω1=60,ω1=70)对于产品及关键件加速度响应数值结果变化趋势,连接部分频率参数对于产品主体及关键件响应峰值影响规律较为单一,随着刚度的升高产品关键件的一阶、二阶共振峰值先增大后减小,产品主体的一阶共振峰值逐渐变大,二阶共振处峰值逐渐变小,当ω1=30 即与缓冲材料频率比接近于1时,有最大的一阶、二阶共振峰值,此时关键件吸收能量最大。按照Den Hartog模型固定点理论[30],此时产品主体的响应最小。

图8 不同连接系统频率参数正切型系统加速度响应数值结果Fig.8 Numerical results of tangent system acceleration response under different connected system frequency parameters

同时,随着ω1的升高产品主体及关键件的一阶、二阶共振峰值点频率均逐渐减小,使得共振区域先变窄后变宽,起到“调频调节峰值点带宽”的作用。当ω1与ωp相差较大时,产品主体及关键件的一阶响应主要受缓冲系统频率参数影响,而二阶响应受连接系统频率参数控制,在它们相接近区域,产品主体及关键件的一阶、二阶响应由它们共同控制。

在包装优化设计过程中,要合理设计或者选择一定连接部分频率参数的缓冲材料,应当使关键件的响应峰值最小或者响应整体能量最小。

3.5 缓冲系统及连接系统阻尼比的影响

图9展示了不同缓冲系统阻尼比(0.02, 0.05, 0.10, 0.20, 0.30)的产品及关键件加速度响应数值模拟结果。从图9可以看出,产品及关键件加速度主要响应随着缓冲系统阻尼比的增加而逐渐减小(若转为线性坐标,二阶响应远小于一阶共振响应,此时主要考虑对主要响应也就是一阶共振响应的影响),两者有着较为一致的一阶共振频率和二阶共振频率,所以缓冲材料能够有效降低产品主体及关键件的响应,这也说明产品包装防护的意义。同时,同一阻尼比下,关键件加速度响应明显高于产品主体的响应。

图9 不同缓冲系统阻尼比的正切型系统加速度响应模拟结果Fig.9 Simulation results of acceleration responses of tangent system except different in the damping ratios of cushion system

图10画出了不同连接部分等效阻尼比(0.02, 0.05, 0.10, 0.20, 0.30)的产品及关键件加速度响应数值模拟结果。从图10可以看出,关键件加速度响应及产品主体的加速度响应谱均随着连接部分等效阻尼比的减低而逐渐增大,虽然两者有着较为一致的一阶共振频率和二阶共振频率。产品主体的二阶响应远小于一阶共振响应,若转为线性坐标,几乎无法观察到二阶响应,此时产品主体主要考虑对主要响应也就是一阶共振响应的影响,而产品关键件有着十分明显的一阶、二阶共振响应,同时,同一阻尼比下,关键件加速度响应明显高于产品主体的响应。

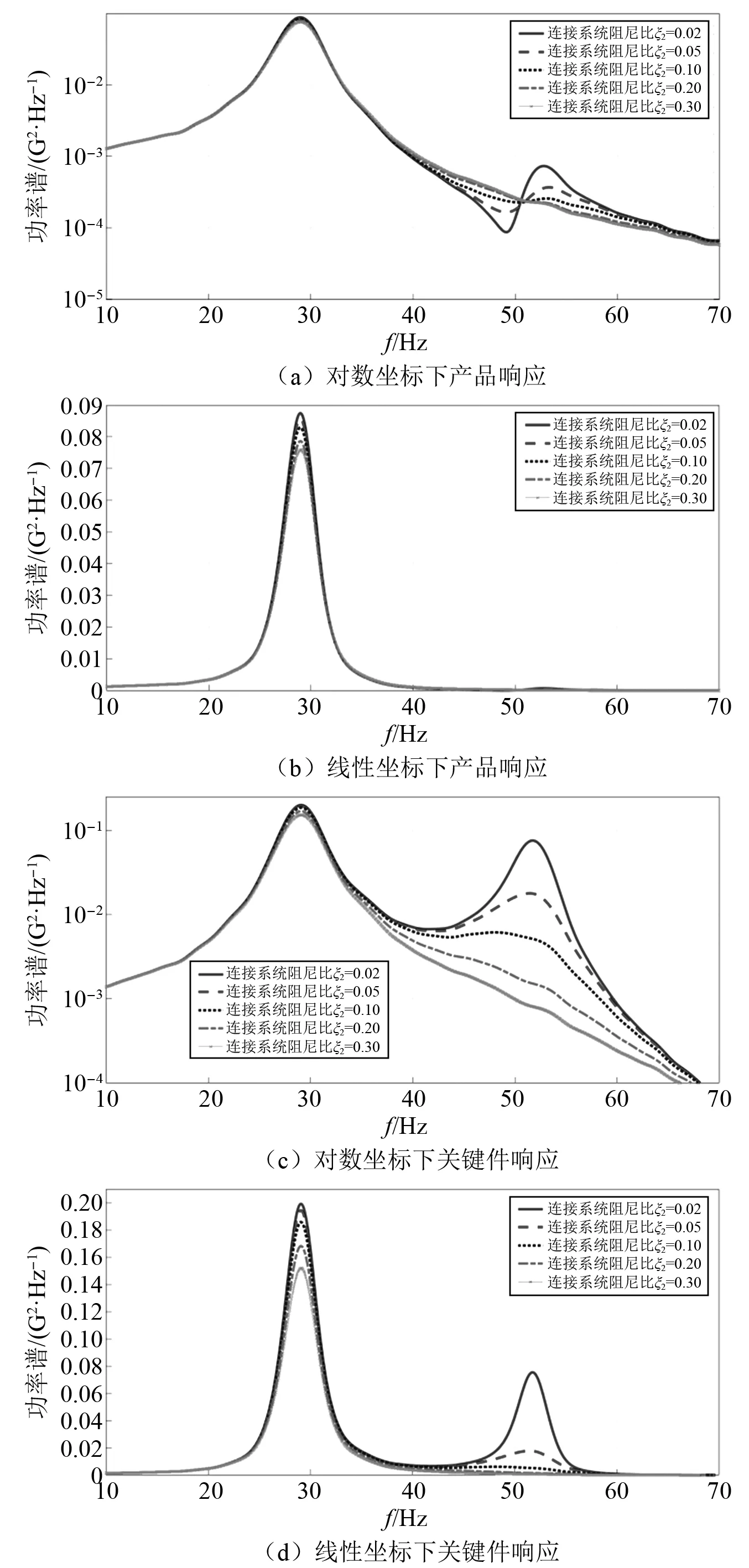
图10 不同连接系统阻尼比的正切型系统加速度响应模拟结果Fig.10 Simulation results of acceleration responses of tangent system with different damping ratios of connected system

4 结 论

本文将考虑产品关键部件的产品包装件建模为两自由度正切型运输包装系统,建立了系统的加速度响应谱理论,同时采用数值模拟的方法验证了理论的有效性,给出了理论工程适用范围,并分析了系统参数和外激强度对于加速度响应谱的影响。研究发现,系统的加速度响应谱对随机激励强度、缓冲材料特征参数、系统阻尼比、频率比及关键件与产品质量比十分敏感,主要结论如下:

(1) 随着激励水平提高,考虑关键件的两自由度正切型运输包装系统的响应均显著增强。正切型系统弹簧的“硬化”非线性作用愈加明显,从而使产品主体的一阶响应峰值点频率及关键件一阶、二阶响应峰值点频率向右边偏移逐渐增大。

(2) 正切型缓冲材料的特征参数β对于产品关键件加速度响应具有明显的“一阶调频,二阶调谐减振”的作用,产品关键件对于特征参数较为敏感,尤其是二阶共振处峰值及一阶共振频率会随着特征参数出现较为单一规律的敏感变化。对于产品主体而言,只需关注特征参数对于其产生一阶共振调频作用。存在一个最佳的缓冲材料特征参数β*,使得关键件的一阶响应峰值最小,也存在另一个最佳特征参数,通过调节响应峰值点带宽的作用,使响应总体能量最小。

(3) 关键件与产品质量比是调节系统响应的关键参数,其升高使得系统产品及关键件加速度一阶响应峰值点频率右移增大,却使两者二阶峰值点频率左移变小,能够有效的降低产品主体及其自身响应峰值频率范围,起到“调频调节峰值点频率带宽”作用。

(4) 缓冲材料和连接体的频率参数对于产品主体及关键件响应频带具有十分明显的调节作用,当两者相接近时,即频率比接近于1,使得产品主体的响应最小,此时关键件响应最大,该结论与单个调谐质量阻尼器响应机制类似。适当提高缓冲材料和连接体阻尼比可以有效减低系统的响应,缓冲材料的阻尼比对缓冲系统频率参数附近的响应有更好的控制效果。