Ultrasonic constitutive model and its application in ultrasonic vibration-assisted milling Ti3Al intermetallics

Guofu GAO,Zongxia FU,Yi WANG,Xianrong PAN,Daohui XIANG,Bo ZHAO

School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo 454000, China

KEYWORDS Dislocation density;Plastic deformation layer;Ti3Al intermetallic compounds;Ultrasonic-K-M hybrid acoustic constitutive model;Ultrasonic vibration-assisted technology

Abstract Ultrasonic vibration-assisted technology is widely utilized in the performance research and manufacturing process of metallic materials owing to its advantages of introducing highfrequency acoustic systems.However,the acoustic plasticity constitutive model and potential mechanism, involving Ti3Al intermetallic compounds, have not yet been clarified.Therefore, the Ultrasonic-K-M hybrid acoustic constitutive model of Ti3Al was established by considering the stress superposition,acoustic thermal softening,acoustic softening and acoustic residual hardening effects according to the dislocation density evolution theory and crystal plasticity theory.Meanwhile,the mechanical behavior of ultrasonic vibration-assisted tension(UVAT)and microstructure of ultrasonic vibration-assisted milling (UVAM)for Ti3Al was investigated.Dislocation density to be overcome from initial deformation to failure of Ti3Al was calculated in UVAT and was verified in UVAM.The results indicated that the Ultrasonic-K-M model showed a good agreement with the experimental data.There was an obviously softening phenomenon after introducing the ultrasonic energy field in the Ti3Al whole deformation region, and the degree of softening was positively correlated with amplitude.Furthermore, the maximum reduction ratio in yield strength of Ti3Al was 16 % and the maximum reduction value in ultimate tensile strength was 206.91 MPa.The elongation rose first and then fell as amplitude enlarged,but only as the vibration was applied in the whole deformation region,the elongation was always greater than 14.58%.In addition,The UVAM process significantly reduced the dislocation density increment to be overcome for Ti3Al material removal by 1.37 times,and promoted dislocation motion and cancellation to make twisted dislocations evolve into parallel dislocations.As the amplitude increased to 4 μm, the depth of the disturbed area of the plastic deformation layer increased by a maximum of 2.5 times.

1.Introduction

Ti3Al intermetallic compounds, as a lightweight and hightemperature resistant rare metal material, have been widely applied in aerospace parts and compressor discs for its excellent mechanical properties even in high-temperature environments, such as good anti-oxidation ability, high strength and improved thrust-weight ratio of the engine.1,2Meanwhile, the main disadvantages of Ti3Al intermetallics included brittleness at room temperature and difficult deformation at high temperatures, which restricted the development of material deformation and manufacturing processes.Furthermore, ultrasonic vibration-assisted manufacturing processes were considered an effective method for material deformation and removal due to the vibration energy being transmitted into the material to change its inherent physical properties.3Therefore,it is necessary to study the underlying deformation mechanism and constitutive behavior of Ti3Al under the action of ultrasonic vibration and to determine the essence of material failure and removal.

Ultrasonic vibration-assisted tension (UVAT) on metallic materials has become one of the effective methods to explore the deformation behavior and mechanical properties under high-frequency vibration due to the elimination of the interference of surface effects.4The introduction of high-frequency vibrations into single-crystal zinc tensile experiments resulted in a significant reduction in flow stress, which was known as the ‘‘Blaha effect”5or ‘‘acoustic plasticity phenomenon”.6UVAT had been studied experimentally on low strength deformable materials such as aluminum alloy,7magnesium alloy,8titanium alloy,9copper10and low-carbon steel.11Meanwhile, ultrasonic vibration-assisted milling (UVAM) was widely used in difficult-to-machine materials such as titanium alloys,3ceramic materials,12and composite materials13to realize material fracture removal.The high frequency vibration of the tool or workpiece exerted a huge energy impact on the material to be machined,14–16which effectively decreased the cutting force,17reduced tool wear18and improved the quality of the surface.19However, less attention and reports had been carried out for high-strength Ti3Al intermetallic compounds in UVAT or UVAM.

The underlying mechanism of UVAT in reducing flow stress during the deformation of materials was explained by the extrinsic factors of ultrasonic action.20The outside causes were referred to as the stress superimposed and acoustic thermal softening phenomenon.When the high-frequency vibration was transmitted into the internal materials and acted on the strain field, where an oscillatory stress field was generated,which was described as a ‘‘stress superposition effect”.Wang,et al.10designed an ultrasonic vibration-assisted uniaxial tension device for copper foil.A remarkable stress reduction was observed in the deformation experiment and explained by stress superposition, which caused a power exponential relationship between the reduction value of yield stress and vibration amplitude.The application of ultrasonic excitation in tension through experiment and finite element calculation was investigated by Daud, et al.,21and found that it did not provide more substantial evidence to explain the influence of UVAT on the aluminum alloy forming process only in terms of stress superposition.Acoustic thermal softening meant a temperature within material raised phenomenon caused by ultrasonic effect.There was an insignificant sample temperature rise during the UVAT experiment of Ti-6Al-4 V in the report by Fartashvand,et al.,22which indicated that ultrasonic softening did not merely have a thermal effect.

The underlying mechanism of flow stress reduction in the UVAT was explained by the migration, storage and annihilation of dislocations, which were called intrinsic factors.23The inherent causes included the ‘‘acoustic softening effect”and‘‘acoustic residual hardening effect”.Under the action of ultrasound,the former was referred to as a reduction in flow stress,but the latter was described as increasing flow stress or decreasing elongation after withdrawal vibration.Dutta,et al.11carried out in situ UVAT test on low-carbon steel to survey its microstructure, and found that acoustic softening was caused by longer dislocations travel distances and dislocation dipole annihilation was enhanced after the superimposed ultrasound.The acoustic softening of three types of aluminum alloys under UVAT was performed by Mao,et al.,24and it was concluded that the mechanism of acoustic softening was related to the activation of dislocations by ultrasonic energy,while the residual hardening was attributed to permanent changes in dislocation density due to dislocation annihilation.Although many investigations have explored the deformation underlying mechanism of different materials under the influence of the UVAT, there was not reached a consensus yet and needed to be further research, especially in the ultrasonic constitutive model of materials.

Several acoustic plastic constitutive models have been proposed, to better describe and predict the plastic deformation behavior of metallic materials in the UVAT.Meng, et al.25proposed a hybrid constitutive model considering both stress superposition and acoustic softening effect,and was calibrated through the UVAT test of the ultrathin superalloy sheet.Prabhakar, et al.26put forward a transverse UVAT method of Al 6063 and developed an ultrasonic effect softening model,which was extended by a dislocation density basic constitutive model.In addition,similar acoustic plastic constitutive models were developed by Siddiq and Sayed27and Yao, et al.,28and the predicted results of the model had good agreement with the experimental data about rheological behavior.However,there was a lack of studies on the acoustic constitutive behavior of Ti3Al under the action of the UVAT.According to the above-related reports mentioned, the constitutive model of Ti3Al was established based on the crystal plasticity theory,thermal activation and dislocation evolution theories, which had a reference value and feasibility.Meanwhile,the ultrasonic vibration mechanism of stress superposition, acoustic thermal softening, acoustic softening and residual hardening effect should be comprehensively considered when the model was constructed.

To investigate the mechanical behavior of UVAT and microstructure of UVAM and build a constitutive model for Ti3Al, firstly, according to the dislocation density evolution theory and crystal plasticity theory, the Ultrasonic-K-M hybrid acoustic constitutive model of Ti3Al was established by considering the stress superposition, acoustic thermal softening, acoustic softening and acoustic residual hardening effects.Secondly, the experimental studies of Ti3Al in the UVAT were carried out based on the self-develop device with ultrasonic vibration uniaxial tension,and to research the material’s mechanical behavior under different amplitudes and application methods.Meanwhile, the numerical models of softening coefficient, hardening coefficient and initial dislocation density variation coefficient with amplitude were constructed to introduce the Ultrasonic-K-M model, which was used to predict the material deformation and failure behavior of Ti3Al under ultrasonic vibration.Finally, the dislocation density and microstructure of UVAM for Ti3Al were explored to verify the correctness of the hybrid acoustic model.In summary, as shown in Fig.1, a flowchart was established to illustrate the logical relationship between the ultrasonic constitutive model and experimental research of Ti3Al intermetallics.

2.Ultrasonic-K-M hybrid acoustic constitutive model

The micro-mechanism and fine mechanical behavior of metal materials during the deformation process was studied by using the dislocation density evolution theory.To obtain the variation relationship between material flow stress and ultrasonic amplitude under the combined effect mechanism of extrinsic factors and intrinsic factors of ultrasonic vibration.The procedure for the establishment of the Ultrasonic-K-M hybrid constitutive model was shown in Fig.2.Firstly, the K-M model about material flow stress–strain without ultrasonic vibration was established, and material coefficients such as dislocation density storage and annihilation were obtained.Secondly,the stress reduction model caused by four effects such as stress superposition, acoustic thermal softening, acoustic softening and acoustic residual hardening effects under ultrasonic energy field was constructed to obtain the numerical relationship of softening coefficient and hardening coefficient with ultrasonic amplitude.Finally, the Ultrasonic-K-M hybrid acoustic constitutive model was established by using different processing of flow stress, because the material was in the ultrasonic energy field and the activation energy required for deformation decreased, which was manifested in a decrease in flow stress.

Fig.1 Flowchart for ultrasonic constitutive model and experimental research of Ti3Al intermetallics.

2.1.K-M model

The physical variations in the rheological behavior of metallic materials during plastic deformation and manufacturing process were mirrored by the crystal plasticity theory, which was formed based on lattice rotation and slip mechanisms, and revealed the change in the stress–strain relationship owing to the dislocation motion within the material.29The proliferation,storage and annihilation of dislocations were followed by the material deformation process, especially for metals with dense hexagonal structures.On the one hand, dislocations produced active motion under the action of external forces.On the other hand, dislocations moved passively by overcoming obstacles under the act of thermal energy.The interaction between dislocations and dislocations or other material defects (e.g.,vacancy,grain boundaries,et al.)was macroscopically characterized as the rheological behavior of material deformation.The nature of the flow stress showed the ability of the material to impede dislocation movement.

The magnitude of the flow stress was understood as the superposition of the non-thermally activated stress component(σnt) inside the material induced by the dislocation motion overcoming the long-range potential barrier, and the equivalent thermally activated stress component(σet)caused by overcoming the short-range potential barrier,30as shown in Eq.(1):

where: f (έ, T) is the thermally activated function (<1) and is used to describe the influence factor of strain rate and temperature effects.The total flow stress(σ)depends on ε,έ,T and s.

The plastic strain rate(έ)was expressed utilizing the Arrhenius equation, which was simplified to a power exponential relationship by Estrin,31as shown in Eq.(2):

where:έ0is the leading frequency factor(s-1),also known as a strain rate of non-thermally activated component,i.e.,the constant associated with έ when σ = σnt.m is the material constant.

Fig.2 Procedure for establishment of Ultrasonic-K-M hybrid constitutive model.

The Kocks-Mecking (K-M) dislocation density evolution theory was used to research the variation of dislocation density with strain within metallic materials, while the change reason for dislocation density was attributed to the dislocation’s realtime storage or annihilation that happened during the motion of dislocations.32,33The material deformation was directly controlled by the dislocation density(ρ)in this theory assumption, and that work hardening and dynamic softening during deformation were caused by dislocation storage and dislocation annihilation, respectively.The dislocation density increment induced by the former was linearly related to the dislocation density of ρ1/2,while the dislocation density decrement caused by the latter was linearly related to the dislocation density ρ.34The dislocation density evolution law was expressed as Eq.(3):

where: M is the Taylor factor or orientation factor.k1is the work-hardening factor to reflect the dislocation storage property, also known as the dislocation storage coefficient, and was usually a constant.k2is the dynamic softening factor to reflect the dislocation annihilation property, also known as the dislocation annihilation coefficient, and depending on the strain rate and temperature.A general expression is k2=k20(έ/έ0)-1/n,where k20is material constant.The exponent n is related to the deformation temperature.

The expression for the dislocation density was obtained by integrating for Eq.(3), and was expressed as Eq.(4).Where ρ0represents the dislocation density inside the material under the initial stress.

Metallic materials generated deformation due to external loading, and the main obstacle to the dislocation slip motion within the grains was the forest dislocation of long-range potential barriers.According to the classical Taylor formula,the real-time relationship between the non-thermally activated flow stress (σnt) of material deformation and the dislocation density (ρ) was obtained,35as shown in Eq.(5):

Fracture failure of the material occurred at the instant when the flow stress reached the peak stress (σp), and it was clear that dσp/dε = 0.The expression of the dislocation density(ρp)inside the material under the peak stress and the initial dislocation density(ρ0)were obtained from Eq.(3)and Eq.(5),respectively.As shown in Eq.(7),the value of σ0takes 0.2%of the strain according to relevant studies.36

2.2.Stress reduction model with ultrasonic vibration-assistance

The crystal lattice of metal materials was divided into defectfree and defective lattice regions.The former was considered to be a uniform elastic–plastic body without impurities, while the latter had crystal defects such as dislocations,lattice distortion, vacancies and interstitial atoms, as shown in Fig.3.

When an ultrasonic energy field was applied during the material deformation, the inert dislocations were rearranged,stored and annihilated after the ultrasonic energy was absorbed by defective lattice regions.The dislocation motion was promoted to change the dislocation density, which ultimately reduced the activation energy required for material deformation.Conversely,the defect-free region was insensitive to the ultrasonic energy field and basically did not absorb energy.10However,the strain field in the material was periodic oscillation when the elastic loading and unloading cycles acted on the defect-free lattice regions by ultrasonic high-frequency vibration, inducing a small temperature rise phenomenon inside the material, which was macroscopically manifested in a decrease of flow stress.

For the two parts of crystal lattice regions of the material,the influence of ultrasonic vibration was attributed to the extrinsic and intrinsic mechanisms of action.It was referred to stress superposition effect, acoustic thermal softening effect and acoustic softening effect, acoustic residual hardening effect, respectively.The coupling of the four effects reduces the deformation activation energy of the material, and the resulting flow stress reduction (Δσ) is expressed as shown in Eq.(8).While due to the softening effect and residual hardening effect under ultrasound were interacting and competing in the process of material deformation,it was difficult to analyze individually.The two were considered as a whole to evaluate the stress variations caused by the intrinsic mechanism of ultrasound.

2.2.1.Stress reduction model considering stress superposition effect

When ultrasonic vibration was applied, the transducer vibrated under the excitation of the ultrasonic signal and its displacement formula was expressed as y(t) = Acos(ωt + φ) = Acos(2πft + φ).The defect-free lattice regionsinside the material were approximated as a desirable elastic–plastic body, and the additional displacement increment during the deformation process of the material was approved as the ultrasonic amplitude.Although high-frequency vibration caused periodic oscillations in the material strain field and stress superposition phenomena, the nature of material deformation was still elastic deformation.The flow stress was linearly related to the strain and elastic modulus according to the generalized Hooke law.Therefore, the relationship between the average stress reduction (Δσss) produced by the stress superposition effect under ultrasonic vibration and the true strain of material was expressed as Eq.(9):

Fig.3 Effect of ultrasonic vibration on different crystal lattice of metal material.

where:E is the elastic modulus(MPa).Asis the average ultrasonic amplitude of the metal material sample (μm).L0is the gauge length of the sample (mm).

After the ultrasonic energy generated by ultrasonic excitation underwent transmission and reflection during the propagation process, most of the ultrasonic energy was transmitted to the metallic material sample.37The expression of acoustic transmission coefficient (λ) was shown in Eq.(10), where the speed of sound chand csare calculated by (Eh/ρh)1/2and (Es/ρs)1/2.

where: Ahis the amplitude of the ultrasonic excitation source(μm), which is usually considered to be the amplitude at the output of the horn.ω is the angular frequency of vibration(rad/s).A general expression is ω = 2πf.

The average ultrasonic amplitude of the metal material sample (As) was obtained and shown in Eq.(12) due to Us= λUh.10

2.2.2.Stress reduction model considering acoustic thermal softening effect

It was found that in the UVAD technology for metallic materials, the internal temperature rise of the material sample increased significantly under the compression process.39,40However, the influence of the surface effect of the material was eliminated in the tension process, and only the volume effect was discussed and it was found that the temperature rise of the material’s surface was very small or negligible.22,25Meanwhile, the instantaneous vibration velocity of the material caused by high-frequency vibration was v(t) = 2πfAsin(2πft + φ), which inevitably led to a change in strain rate.The strain rate(έult)induced by superimposed ultrasonic vibration was expressed as:

where:vcis the beam displacement rate(mm/s).ΔL is the value of sample deformation (mm).

The deformation process of metal at high strain rates was accompanied by the phenomenon of adiabatic temperature rise inside the material,41and the numerical value of the adiabatic temperature rise (ΔT) was exponentially positively correlated with the strain rate.The heat increment per unit volume of the material was expressed as Q = ρsCpΔT, where Cpis the mass-specific heat capacity (J∙kg-1∙K-1) of the sample material.Obviously, the higher the instantaneous strain rate of the material was subjected to,the more significant the internal temperature rise and the larger heat was collected in the material.

The material was subjected to axial loading force in the tension process and its deformation rate was relatively slow,so it was considered that the sample was loaded under the static strain rate.The strain rate increased after superimposing ultrasonic vibration, έultwas 822.68 s-1according to Eq.(14) when the amplitude and frequency were 6.55 μm and 20 kHz.At the same time, the adiabatic temperature rise of Ti3Al was only 275 K when the instantaneous strain rate was 5500 s-1based on the high strain rate Hopkinson compression bar experiments.42The temperature rise caused by ultrasound was extremely small and insufficient to induce a significant drop in flow stress.Therefore, the flow stress reduction caused by the acoustic thermal softening effect was negligible.In other words, the expression of Δσatwas:

In the ultrasonic vibration-assisted subtractive machining of metal materials, the increment in the instantaneous strain rate to which the material was subjected was not only caused by ultrasonic vibration but also related to the material removal speed.The temperature inside the material rose by the coupling action of the two, which effectively promoted the material softening and was beneficial to further reducing the flow stress of the material deformation.

2.2.3.Stress reduction model considering acoustic softening and acoustic residual hardening effects

The defective lattice regions inside the material after applying ultrasonic vibration, such as dislocations began to absorb a large amount of ultrasonic energy due to the inelastic scattering mechanism, which made the dislocation activation energy decrease.In addition,proliferation,entanglement,and generation of relative motion of dislocation caused variations in dislocation density in the crystal and induced acoustic softening and acoustic residual hardening phenomena in the material.The storage and annihilation capacity of dislocations followed and changed with the ultrasound field.43The dislocations density evolution law in the ultrasonic energy field was expressed as:

where: ηk1and ηk2reflect the storage and annihilation properties of additional dislocations induced by ultrasonic vibration,respectively.The coefficients ηk1and ηk2represent the various ratios of k1and k2under the ultrasonic energy field, respectively,and the magnitudes are related to the amplitude and frequency of the ultrasonic excitation.

The expression for the dislocation density inside the material under the action of ultrasonic vibration(ρult)was obtained by integrating Eq.(16), as shown in Eq.(17):

where: η0is the variation coefficient of the initial dislocation density of the material under the ultrasonic energy field.

Combined with Eq.(5)and Eq.(17),when the acoustic softening effect and residual hardening effect were considered together,the material flow stress under the ultrasonic intrinsic mechanism (σult-im) was expressed as Eq.(18):

2.3.Ultrasonic-K-M hybrid acoustic constitutive model

The activation energy required for deformation decreased as the material was in an ultrasonic energy field, manifested in a decrease in flow stress.Based on Eq.(6), Eq.(13), Eq.(15)and Eq.(19), the Ultrasonic-K-M hybrid acoustic constitutive model of the material under ultrasonic vibration was established by using difference processing.The flow stress of the material under ultrasonic vibration (σult) was calculated integrated as follows:

Combining Eq.(7)and Eq.(17),the expressions of the initial dislocation density (ρult0) and the peak or fracture failure dislocation density(ρultp)inside the material after applying ultrasonic vibration was obtained and shown in Eq.(21).

where: k1, k2, m and ρ0are the parameters to be determined,which are obtained by fitting the material mechanics experiment without ultrasonic vibration.ηk1,ηk2and η0are the functions related to the amplitude of the horn (Ah), which are achieved by ultrasonic vibration-assisted tension mechanical response experiments.

3.Experimental schedule

3.1.Experimental device

Fig.4 showed the UVAT and UVAM of the Ti3Al experimental system.A self-develop device with ultrasonic vibration uniaxial tension for Ti3Al with a resonant frequency of 20 kHz was installed directly on the universal testing machine (YNS-300, SINOTEST, China), as shown in Fig.4(a).A support frame and a resonance system were composed in the device,and the former was connected to the upper chuck on the universal testing machine to make sure that the material was subjected to static tensile loads.The latter included an ultrasonic power source,transducer,a cylindrical-conical composite horn of the upper-end, a stepped horn of middle-end, a Ti3Al sample and a stepped horn of lower-end.A high-frequency electrical oscillation signal was supplied by ultrasonic power and was converted into mechanical vibration by the piezoelectric transducer.The vibration was amplified and transmitted to the inside of the Ti3Al sample by the upper-end and middle-end horns.The horn and sample were fixed through a threaded connection to transmit ultrasonic vibration amplitude.The lower-end horn was connected to the down chuck on the universal testing machine.The universal experiment machine adopted the force loading control method, the force speed was set to 0.2 kN/s,corresponding to a quasi-static strain rate of about 1×10-3s-1.A high-speed camera(VM-Z1,Keyence,Japan) was employed to real-time monitor the tensile process,and a data acquisition instrument and electro-hydraulic servo control system measurement and control software were deployed for data acquisition and treatment of the loading test force and displacement.

The experimental study on UVAM of Ti3Al was conducted by the vertical machine center VMC-850, as shown in Fig.4(b).The experiment instrument mainly consisted of an ultrasonic generator, a wireless transmission device, a longitudinal-torsional ultrasonic vibration system, coated milling cutters, workpiece Ti3Al, piezoelectric dynamometer(9257B,Kistler,Switzerland).A certain high-frequency electrical oscillation signal was generated by the ultrasonic generator and transmitted to the wireless transmission system which include the excitation coil fixed on the spindle and the induction coil set on the ultrasonic tool holder.A high-frequency mechanical vibration longitudinally was transformed by the piezoelectric transducer after receiving the electrical signal.A horn with spiral grooves was designed to amplify and convert the amplitude.The vibrating coated milling cutters were driven by the machine tool spindle to perform side milling on the workpiece Ti3Al.

Fig.4 UVAT and UVAM for experimental system Ti3Al.

3.2.Experimental material

The ingot with a nominal composition of Ti-22Al-24Nb-0.5Mo (at%) was prepared by the vacuum arc remelting method.The bar of a diameter of 40 mm was produced after one hot forging and twice hot rolling.Subsequently,the rolled bar was cut into a cylindrical shape of ∅15 mm × 90 mm.According to the dumbbell-shaped sample standard GBT 228 1–2010, the tensile sample and cuboid workpiece(20 mm × 15 mm × 10 mm) of Ti3Al were processed by considering the uniformity of vibration transmission, the space limitation of the experimental machine, and a connection between the sample and the horn, as shown in Fig.5.

The chemical composition of Ti3Al intermetallics was listed in Table 1.The original metallographic structure of the SEM image for Ti3Al was shown in Fig.6, and it belonged to the equiaxed organization in the typical three-phase structure,which consisted of α2phase (D019structure based on Ti3Al),O phase (Cmcm structure based on Ti2AlNb) and B2 phase(BCC structure based on allotropic titanium element), respectively.There was a small amount of equiaxed α2phase and a large amount of fine lamellar O phase was uniformly distributed in the B2 matrix.As shown in Fig.7, the phase analysis of original Ti3Al intermetallics was detected though an Xray diffractometer (D8 Advance, Bruker, Germany).

3.3.Experimental program

To analyze the action mechanism of Ti3Al in the UVAT process under ultrasonic energy field and vibration loading method on material deformation.Firstly, the mechanical behavior of Ti3Al at different amplitudes was investigated.Fig.8 revealed the relationships between Ah,Asand the output of ultrasonic power, where Ahwas the amplitude of horn in Ti3Al UVAT,and was directly measured by laser displacement sensor(LK-G10,Keyence,Japan).Aswas the amplitude of the Ti3Al sample in UVAT,according to the energy law of acoustic wave transfer between heterogeneous materials and Eq.(12).There was a linear positive correlation relationship between the amplitude of the Ti3Al sample and ultrasonic power.

Fig.5 Ti3Al sample and Ti3Al workpiece in UVAT and UVAM.

Table 1 Chemical composition of Ti3Al intermetallics.

Fig.6 Metallographic structure of original Ti3Al intermetallics.

Fig.7 Phase analysis of original Ti3Al intermetallics.

Secondly,the mechanical behavior of Ti3Al under different vibration loading methods was studied,such as a full vibration at the whole deformation region and an intermittent vibration at different deformation regions.The former referred to the application of ultrasound during the whole tensile process,while the latter referred to the application of vibration only in the elastic region or plastic region.As shown in Fig.4(a),intermittent vibration of Ti3Al was achieved by turning on or turning off the ultrasonic power source at the yield point and fracture point.Meanwhile,an ordinary tensile experimental study of Ti3Al was carried out and found that the material yield and fracture loads were 21.8 kN and 23.19 kN, respectively,and the corresponding true strains at yield and fracture were approximately 0.124 and 0.269.The experimental testing parameters were listed in Table 2.At least three sets of experiments were conducted under each process parameter to ensure the accuracy of the experimental results.

The tool parameters and machining parameters for UVAM of Ti3Al were listed in Table 3.The relationships between Atand the output percentage of ultrasonic power was shown in Fig.8,where Atwas the amplitude of the tool in Ti3Al UVAM and measured by the laser displacement sensor.As the amplitude measurement of the independent acoustic system (middle horn and the output end of milling cutter),Ahand Atwere easy to drift along with the variation of load after the acoustic system was fixed on a universal testing machine or machining center.While the trend of load to amplitude variation was consistent in the experimental systems of Ti3Al UVAT and UVAM.To reduce the difference between actual cutting conditions and tensile test experimental conditions, on the one hand,the influence of load change and flutter of universal testing machine and machining center on the acoustic system was ignored, i.e., the measured values of Ahand Atwere assumed to remain unchanged during the experiment.On the other hand, UVAT and UVAM experiments for Ti3Al were performed using the same ultrasonic power.For output percentage of ultrasonic power 20 % and 30 %, Asand Atwere 1.31 μm, 3.93 μm and 1 μm, 4 μm respectively.This assumption was beneficial to construct the Ti3Al constitutive model in UVAT and the verify the acoustic softening phenomenon of Ti3Al in UVAM.

Fig.8 Relationship between ultrasonic amplitude and ultrasonic power.

Table 2 Experimental testing parameters of Ti3Al in UVAT.

Table 3 Experimental testing parameters of Ti3Al in UVAM.

To explore the evolution law of Ti3Al microstructure caused by ultrasonic vibration, on the one hand, the microstructure of the processed surface of Ti3Al was characterized along the xoy plane, such as 2D-SEM (Merlin Compact,Zeiss, Germany), 3D morphology (OLS5100 Confocal, Olympus, Japan) and TEM (Tecnai G2 F30, FEI, USA).On the other hand, the metallographic specimens were prepared of workpiece Ti3Al along the feed speed (vf) direction, and the metallographic organization along the xoz plane was observed after slicing,inlaying,mechanical grinding,polishing and etching processes.The corrosion solution was the Kroll reagent with a ratio of 4 vol%HF + 5 vol%HNO3+ 91 vol%H2O,and the corrosion time was 15 s.Meanwhile,after wire cutting,mechanical grinding(thickness 50 μm),punching wafer(diameter 3 mm),double spray electrolytic thinning and liquid nitrogen cooling polishing, the TEM observations were performed at an accelerating voltage of 300 kV.The volume fraction ratio of perchloric acid,methanol and normal butanol in electrolyte formulation was 6: 60: 34.

4.Findings and results

4.1.The effect of ultrasonic vibration on the mechanical behavior

4.1.1.Influence of vibration method on mechanical behavior

The true stress–strain curve of Ti3Al and the maximum value of flow stress reduction during plastic deformation were shown in Fig.9, when ultrasonic vibration was applied during the whole deformation, elastic deformation and plastic deformation regions.

The material underwent significant softening and the amount of flow stress drop was 151.97 MPa when the vibration was applied in the whole deformation region of Ti3Al.Acoustic softening and acoustic residual hardening coexisted in the deformation process of the material after introducing vibration in the elastic deformation region of Ti3Al.Acoustic softening was manifested by the reduction of stress and earlier occurrence of yield and fracture points.Acoustic residual hardening was exhibited after the vibration was stopped,compared with that without ultrasonic vibration, the stress in the plastic deformation process of the material had a reverse increase trend.At this time, the flow stress decreased by-29.18 MPa.When vibration was applied to the plastic deformation region, the curve of Ti3Al during plastic deformation was parallel to the curve of As= 0 μm.The slope remained unchanged and suggested that ultrasonic vibration did not change the strain hardening rate of the material.

4.1.2.Influence of ultrasonic amplitude on mechanical behavior

The rheological curve after applying ultrasonic vibration in the whole deformation region was shown in Fig.10(a), compared with the curve of As= 0 μm, the true stress–strain curve of Ti3Al appeared an apparent overall downward deviation.The macroscopic rheological behavior of Ti3Al showed the phenomenon of flow stress reduction.

With amplitude increased, the variation law of the flow stress reduction in the elastic or plastic deformation region of the material was not consistent.As shown in Fig.10(b),in the curve of the plastic deformation region,the stress reduction of Ti3Al was monotonically increasing with amplitude,and the maximum stress reduction was 206.13 MPa under the Aswas 6.55 μm.However,in the curve of the elastic deformation region,the stress reduction of Ti3Al did not rise but fell with the increase of the amplitude.This revealed that there was a critical value for the deformation energy storage required to overcome material yielding and to overcome material fracture.When the deformation energy was lower than the critical value, the dislocation density increased with the increase of ultrasonic energy.After the critical dislocation density was reached,the dynamic recrystallization mechanism of the material was activated at the critical strain.When the deformation energy was higher than the critical value, with the ultrasonic energy increased, the deformation energy storage provided the driving force for dynamic recrystallization, which promoted the occurrence of dislocation cancellation and the rearrangement of the dislocation structure,resulting in dislocation reduction and dislocation density decreased.For this reason,the material flow stress reduction decreased with the increase of amplitude before the dynamic recrystallization, while the material flow stress reduction increased with the rose in amplitude after the dynamic recrystallization.This explanation was consistent with the variation trend of stress reduction with amplitude in Fig.10(a).

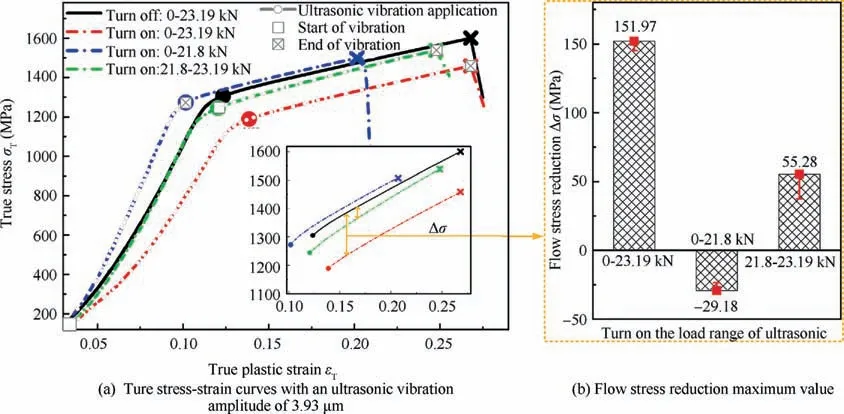
Fig.9 Ture stress–strain curves and flow stress reduction maximum value at different deformation regions.

Fig.10 Ture stress–strain curves and flow stress reduction maximum value of Ti3Al at different amplitudes.

4.2.Determination parameters of the ultrasonic-K-M model

4.2.1.Pending parameters and functional relationship

The coefficients such as k1, k2, m, ρ0in the Ultrasonic-K-M hybrid acoustic constitutive model were obtained by parameter identification in the mechanical response experiment of Ti3Al without ultrasonic vibration.The functions in the model reflecting the vibration characteristics,such as ηk1,ηk2,η0,were derived by fitting the data experimentally to the mechanical response of Ti3Al under different ultrasonic amplitudes.

The plastic segment of the Ti3Al flow stress–strain curve without ultrasonic vibration was taken,and the material rheological relationship between the equivalent plastic strain (εp)and the true stress was obtained by the treatment for the yield point strain to subtract from all strains.The undetermined coefficients in the K-M model were calculated according to the parameter identification of the experimental results and were listed in Table 425,44–46.

The relationship curves of Ti3Al between the flow stress,stress reduction and equivalent plastic strain were selected when the ultrasonic vibration was applied to the whole deformation.Firstly,nonlinear curve fitting was used to identify the numerical solutions of ηk1, ηk2and η0under different amplitudes.And then to develop the coupling relationship between the acoustic softening effect, the acoustic residual hardening effect and the amplitude.The polynomial fitting was used to build the functional relationship between ηk1, ηk2, η0and Ah,as shown in Eq.(22):

Table 4 Parameter values in K-M model.

4.2.2.Error analysis of model

The experimental conditions and acoustic parameters were substituted into Eq.(23),and the predicted curves of equivalent plastic strain and flow stress for Ti3Al at different amplitudes were plotted.According to the predicted data and experimental data, the average absolute relative error (AARE) at different amplitudes was calculated as Eq.(24)to verify the accuracy of the Ultrasonic-K-M model.The predicted curve,experimental data and the AARE were shown in Fig.11.

where Eiand Piare the experimental data and predicted value,respectively.

It was seen from Fig.11(a)that the predicted curves were in excellent agreement with the experimental data.The deviation between the predicted and experimental values increased with increasing amplitude.As shown in Fig.11(b),AARE was only 0.33 % when Aswas 0 μm, and AARE from 0.8 % to 1.57 %with Asincreased from 1.31 to 6.55 μm.Therefore, the established Ultrasonic-K-M hybrid acoustic constitutive model had satisfactory prediction accuracy and did effectively predict the deformation behavior of Ti3Al materials under the ultrasonic amplitude range 0–6.55 μm.When the amplitude exceeded 6.55 μm, possible deterioration of model prediction accuracy occurred due to the increased AARE, so it was necessary to make a comprehensive analysis in conjunction with the actual upper limit of relative error.As the fitted function shown in Fig.11(b), AARE increased along with the amplitude but it was less than 2 % (for As= 15 μm, AARE = 1.87 %), which demonstrated that the proposed constitutive model was applicable relatively for ultrasonic amplitudes beyond 6.55 μm.

4.3.Effect of ultrasonic vibration on material property

The variation of yield stress (YS) and ultimate tensile stress(UTS) with amplitude were shown in Fig.12(a), 12(b), and 12(c), when the ultrasonic vibration was applied to the elastic,plastic and whole deformation regions of the material, respectively.Compared with no ultrasonic vibration, the YS and UTS of Ti3Al decreased to different degrees after the applied vibration, and the reduction increased with the increase of amplitude.When the amplitude was 6.55 μm, the UTS reduction of Ti3Al in the elastic, plastic and whole deformation regions was 76.84 MPa,104.21 MPa,and 206.91 MPa,respectively, while the YS reduction ratio of Ti3Al in plastic and whole deformation regions were 10%and 16 %,respectively.This showed that the introduction of the ultrasonic energy field was beneficial to promote acoustic softening and plastic deformation of the material.The larger the amplitude, the more energy absorbed by the dislocation and the more pronounced the material softening effect.Meanwhile,the longer the deformation time applied by ultrasonic excitation, the more significant the elastic loading and unloading of the defect-free lattice region in the material,and the more intense the periodic oscillation of the strain field and the stress superposition phenomenon, which induced a greater reduction of YS and UTS.

Fig.11 AARE of experimental data and predicted curve under different amplitudes.

Fig.12 Material property of Ti3Al at different amplitudes.

The residual hardening or softening phenomenon caused by the ultrasonic plastic effect was used for the material elongation to reflect.The relationship between elongation of Ti3Al and amplitude was shown in Fig.12(d).The elongation fell first and then rose as amplitude enlarged under the vibration applied in the elastic region, but the numerical values were lower than the elongation of the material without ultrasonic vibration(14.58%).The decrease in elongation suggested that the residual hardening phenomenon occurred in the material by ultrasonic vibration, and this point was also confirmed by the stress reduction with a negative value in Fig.9(b).The elongation was 15.71 %, 14.59 % and 13.59 % under the vibration was applied in the plastic region, when the amplitudes were 1.31 μm, 3.93 μm and 6.55 μm, respectively.It showed that the ‘‘competitive”between acoustic softening and acoustic residual hardening existed in the material deformation under ultrasonic excitation.The acoustic residual hardening and acoustic softening effects were dominant at small and large amplitudes, respectively.The elongation rose first and then fell as amplitude enlarged under the vibration applied in the whole region, but it was still greater than 14.58 %.The elongation reached a maximum value of 15.67 % when the amplitude was 1.31 μm,which had 7%higher than that without ultrasound.The elongation and plastic deformation ability of Ti3Al were improved by the application of appropriate ultrasonic vibration, while excessive ultrasonic energy had an inhibitory role in enhancing the elongation of the material.It was worth noting that the change of material properties with the introduction of the ultrasonic energy field was dominated by the amplitude and the region of vibration application.On the other hand,there was no direct evidence that the ultrasonic frequency and vibration duration did not affect the ultrasonic softening effect.Therefore, to systematically explore the effect of the ultrasonic energy field on material properties,the subsequent research on the softening mechanism of materials under different ultrasonic frequencies should be considered.

4.4.Effect of ultrasonic amplitude on dislocation density

Fig.13 Dislocation density and TEM of Ti3Al with different amplitudes.

Fig.14 SEM of surface microstructure of Ti3Al under different amplitudes.

Fig.15 SEM of subsurface microstructure of Ti3Al under different amplitudes.

Based on the constructed Ultrasonic-K-M model, combined with Eq.(21)and Eq.(22),the theoretical calculation of the initial dislocation density (ρult0) and the fracture failure dislocation density (ρultp) in UVAM Ti3Al were shown in Fig.13(a).The dislocation density to be overcome for the initial deformation and fracture failure of the material without ultrasonic vibration assistance were 2.37 × 1011m-2and 8.87×1011m-2,respectively.The dislocation density proliferation of Ti3Al to achieve material removal was 6.50 × 1011m-2,indicating that a large number of dislocations were accumulated inside the material after fracture failure.The observation of dislocation on the processed surface of Ti3Al was shown in Fig.13(b),and it was found a large number of entangled dislocations and accumulation formed dislocation walls.

The initial deformation dislocation density and the fracture failure dislocation density of Ti3Al were significantly reduced after applying ultrasonic vibration.As the amplitude increases from 1 μm to 4 μm, the increment of dislocation density overcome by material removal decreased from 6.32 × 1011m-2to 4.73 × 1011m-2.Meanwhile, the winding dislocations of the machined surface evolved into parallel dislocations, as shown in Fig.13(c).This showed that the dislocation motion was promoted under the ultrasonic energy field, and the cancellation probability of dipole dislocations was expanded and the proliferation of dislocation density was reduced.Although the actual data on dislocation density was not obtained in the experimental test due to technical reasons.By comparing Fig.13(b) with Fig.13(c), it was intuitively found that the number of entangled dislocations distributed on both sides of the dislocation wall in Ti3Al was significantly reduced with ultrasonic vibration assistance.To some extent, it verified the established theory and the softening effect of the ultrasonic energy field in material deformation.

4.5.Effect of ultrasonic amplitude on microstructure

To further illustrate the softening effect of the ultrasonic energy field in material deformation, the microstructure of the machined surface and subsurface of Ti3Al were observed,as shown in Fig.14 and Fig.15, respectively.The 2D and 3D surface morphology and metallographic structure along the feeding direction of the material without ultrasonic vibration were shown in Fig.14(a),Fig.14(b)and Fig.15(a).It was found the large chips adhered to the linear tool marks on the machined surface.The surface roughness was 0.858 μm, and the depth of the disturbed area of the plastic deformation layer was 10.23 μm, whereas the depth of the highly disturbed area was 2.74 μm.

The surface morphology of the material after applying ultrasonic vibration was a wavy line processing texture.With the increase of amplitude, the depth of texture expanded,meanwhile, both the bonded swarfs of the machined surface and surface roughness decreased.It was indicated that the application of the ultrasonic energy field was beneficial to obtain a more excellent material surface.However, as the amplitude increased from 1 μm to 4 μm, the depth of the disturbed area of the plastic deformation layer in the material subsurface increased from 12.33 μm to 25.14 μm,and the highest depth of the highly disturbed area reached 5.24 μm.At the same time,the phase structure in the highly disturbed area was refined and stretched, and microcracks appeared in the α2phase and transformed into a defective α2phase.

This phenomenon was explained from the following two aspects: The brittle α2phase was easier to absorb ultrasonic energy,and was more likely to generate defects,which evolved into the primary position of material fracture failure.47In addition, according to Eq.(23) and Fig.11(a), the larger the ultrasonic amplitude, the more obvious the ultrasonic softening effect,resulting in that the material underwent more significant plastic deformation and appeared deeper depth of the disturbed area of the plastic deformation layer.

5.Discussion

The mechanical behavior and material property of the material were changed by the introduction of ultrasonic energy field during Ti3Al UVAT.Not only the macroscopic stress during deformation but the yield strength and ultimate tensile strength of Ti3Al showed a downward trend.The mechanism behind this experimental phenomenon was closely related to the promotion of dislocation movement and the opening of the slip system in Ti3Al.Random and disordered dislocations were distributed at the grain boundaries and generated entanglement and accumulation when the material was deformed without ultrasonic vibration.However, after the material deformation process was superimposed with ultrasonic vibration, the dislocations located in defective lattice regions began to absorb ultrasonic energy.On the one hand, more inert dislocations began to move actively and improved the average dislocation speed.On the other hand,the possibility of encountering dipole dislocations expanded to promote dislocation annihilation.The decrease in dislocation density at the grain boundaries resulted in a drop in the deformation energy storage that was overcome during Ti3Al deformation, which promoted the start-up of all slip systems.Meanwhile, the ultrasonic energy was positively correlated with the amplitude, and the larger amplitude, the more energy was available for dislocation absorption and the more plastic deformation was likely to occur.Therefore,the effect of the ultrasonic energy field made it easier for Ti3Al to overcome internal stresses and undergo material softening, yielding and fracture failure.

Due to the introduction of ultrasonic vibration in UVAM of Ti3Al, the processed surface showed wavy line textures,small surface roughness, deep plastic deformation layer and defective α2phase structure.The mechanism behind the experimental phenomena was discussed from both macro and micro perspectives.From a macroscopic point of view, the addition of ultrasonic vibration was equivalent to exerting highfrequency pulse impact on the processing system.The change of tool tip trajectory was the main reason for regular microtexture.The impact energy instantly softened the surface to be machined in the chip area, reduced the local deformation of Ti3Al during cutting, and achieved the uniform removal of materials.The deeper Ti3Al plastic deformation layer was caused by repeated impact and ironing effect.From the microscopic point of view,the dislocation motion was promoted and the dislocation morphology was changed under the ultrasonic energy field.The entangled dislocations were released and unfolded, and the cancellation probability of dipole dislocations was enlarged.Finally, the amount of dislocation density multiplication achieved by Ti3Al for material removal was reduced.

6.Conclusion

Based on the self-develop device with ultrasonic vibration uniaxial tension,the mechanical behavior of Ti3Al was performed when the ultrasonic excitations with different amplitudes were applied in the material whole deformation,elastic deformation and plastic deformation regions.The Ultrasonic-K-M hybrid acoustic constitutive model of Ti3Al was established to predict material deformation and failure behavior.Meanwhile, the microstructure research of ultrasonic vibration-assisted milling of Ti3Al was carried out to verify the correctness of the hybrid acoustic model.According to the experimental results and theoretical analysis, several conclusions were drawn as follows:

(1) Based on the dislocation density evolution theory and crystal plasticity theory, the Ultrasonic-K-M hybrid acoustic constitutive model of Ti3Al was established by considering the stress reduction under the coupling function of the stress superposition,acoustic thermal softening, acoustic softening and acoustic residual hardening effects.The predicted results from the model showed a good agreement with the experimental data.The average absolute relative error(AARE)was positively correlated with amplitude, and AARE was only 1.57 % when Aswas 6.55 μm.

(2) Acoustic softening and acoustic residual hardening coexisted in the deformation process of the material after applying vibration in the elastic deformation region of Ti3Al.It was found that the introduction of ultrasound did not change the strain hardening rate of the material when vibration was applied in the plastic deformation region of Ti3Al.

(3) The yield strength (YS) and ultimate tensile strength(UTS) both decreased after the ultrasonic vibration was introduced in the whole deformation region of the Ti3Al, and the reduction was positively correlated with amplitude.The maximum reduction ratio in YS of Ti3-Al was 16 % and the maximum reduction value in UTS was 206.91 MPa.As the vibration was applied in the whole deformation region, regardless of the magnitude of amplitude,the elongation rose first and then fell as amplitude enlarged, and the values always were greater than 14.58 % (the elongation of Ti3Al without ultrasonic vibration).

(4) The UVAM process significantly reduced the dislocation density increment to be overcome for Ti3Al material removal by 1.37 times (the dislocation density proliferation decreased from 6.50×1011m-2to 4.73×1011m-2as the ultrasonic amplitude increased from 0 μm to 4 μm).Under the action of the ultrasonic energy field,the twisted dislocations on the machined surface evolved into parallel dislocations distributed near the dislocation wall, and dislocation motion and dislocation cancellation were promoted.

(5) The disturbed area depth of the processed subsurface plastic deformation layer for Ti3Al material was only 10.23 μm without ultrasonic vibration assistance.As the amplitude increased to 4 μm, the depth of the disturbed area of the plastic deformation layer increased by a maximum of 2.5 times.The grains and phase structure on the highly disturbed area were more refined under the acoustic softening effect, and some α2phase evolved into the defective α2phase, which was the primary failure position for material removal.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (Nos.51875179 and 52275419).