基于PCA-GRD-LWR模型的海上油田中长期最大电力负荷预测

王艳松　申晓阳　李强　李雪

摘要：年最大負荷是合理配置电源、确定系统装机容量的重要理论依据，精确的预测结果可以减少海上油田平台的设备投资和运行成本。年最大负荷与油田产量、开采阶段等影响因素密切相关，分析影响负荷需求的特征量与最大负荷的内在联系及变化趋势，用主成分分析法对特征量进行处理，将相关性强的特征量转化为互不相关的主成分；计算各主成分与最大负荷之间的灰色关联度，根据关联程度确定回归模型的权重；建立基于灰色关联度的局部加权回归预测模型，并用粒子群算法优化局部加权回归模型的参数。以某海上油田的历史数据为例进行校验分析，结果表明，中长期负荷预测误差均小于3%，验证了所提方法的有效性，给出了未来10 a的最大负荷预测结果。

关键词： 海上油田； 电力负荷预测； 主成分分析； 灰色关联度； 局部加权回归； 粒子群优化

中图分类号：TM 715 文献标志码：A

引用格式：王艳松，申晓阳，李强，等.基于PCA-GRD-LWR模型的海上油田中长期最大电力负荷预测［J］.中国石油大学学报（自然科学版），2023，47（2）：129-135.

WANG Yansong， SHEN Xiaoyang， LI Qiang， et al. Forecasting of medium and long-term maximum power load for offshore oilfields based on PCA-GRD-LWR model ［J］. Journal of China University of Petroleum （Edition of Natural Science），2023，47（2）：129-135.

Forecasting of medium and long-term maximum power load for offshore oilfields based on PCA-GRD-LWR model

WANG Yansong1， SHEN Xiaoyang1， LI Qiang2， LI Xue3

（1.New Energy College in China University of Petroleum（East China）， Qingdao 266580， China; 2.CNOOC， Beijing 100010， China; 3.CNOOC Research Institute， Beijing 100028， China）

Abstract： The annual maximum load is an important theoretical basis for the reasonable allocation of power supply and determination of the installed capacity of the system. Accurate forecasting results can reduce the equipment investment and operating cost of the offshore platform. The annual maximum load is closely related to such influencing factors as the oilfield production and the mining stage. The internal connection and variation trend of each characteristic quantity which affect the power load demand and the maximum load were analyzed， and the principal component analysis （PCA） was used to process the characteristic quantities， transforming the characteristic quantities with strong correlation into unrelated principal components. The grey relational degree （GRD） between each principal component and the maximum load was calculated， which was used to distribute different weights to regression results. The locally weighted regression （LWR） forecasting model based on the grey relational degree was established， and the parameter in the LWR model was optimized by the particle swarm optimization （PSO）. The effectiveness of the proposed method was verified by analyzing the historical data of an offshore oilfield. The results indicate that the prediction error of the medium and long-term load forecasting is less than 3%， and the maximum load forecasting results in next 10 years are presented.

Keywords： offshore oilfield; power load forecasting; principal component analysis; grey relational degree; locally weighted regression; particle swarm optimization

相较于陆上电力系统，海上油田电力系统容量相对较小、工作环境恶劣，对供电可靠性要求高［1］，且用电需求与油田产量、开采阶段、油藏性质等多种因素相关。海上平台大多体积有限、电气设备比较集中，精确的中长期负荷预测可以指导进行合理的网络布局规划和调度策略的制定［2］，提高设备的运行效率，减少投资和运行成本。目前负荷预测方法主要分为传统方法与智能方法两类。传统方法主要有时间序列、回归分析法等，其建模简单但对原始数据平稳性要求高；智能方法主要有灰色预测、神经网络、支持向量机、组合预测法等，其建模复杂但对非线性数据处理能力强。Li等［3］用数据驱动的线性聚类方法对数据进行分类，对每个数据集分别采用时间序列进行预测，对各数据集的预测结果求和得到最终预测值。刘升伟等 ［4］对高斯过程回归进行改进，以准确捕捉电力负荷的时变特性。韦钢等［5-6］采用盲数理论改进传统的线性回归模型以描述负荷变化规律的不确定性，给出了预测值的可能区间及相应可信度。灰色预测模型所需建模信息少，适合处理小样本问题［7-9］。王宁等 ［10］采用网格搜索法对支持向量机模型参数进行优化，对年最大降温负荷进行预测。肖其师等［11］将分位数回归与神经网络相结合，给出了用电量的预测区间。组合预测法充分利用各种算法的优点，将几种算法有机结合，构建综合的预测模型。Fan等 ［12］提出了一种混合模型EMDSVRAR，综合了EMD的平滑去噪能力、AR模型预测未来趋势的能力和SVR的非线性学习能力。刘明等 ［13］将支持向量回归与多元线性回归进行组合，对负荷进行了区间预测，其权重可以根据最新的预测结果进行自适应调整。笔者以海上油田电力系统的年最大负荷为研究对象，以年为周期對其进行预测，已有的历史数据样本少、无周期性规律，各影响因素之间有较强的相关性。针对这些特征采用主成分分析法对影响最大负荷的特征量进行处理，将相关性强的原始变量转化为互不相关的新变量；将灰色关联度融入到局部加权回归模型中，在解决线性回归欠拟合问题的同时，充分考虑变量与负荷变化的相近程度对预测结果的影响；采用粒子群算法对局部加权回归模型中的参数进行优化以提高预测精度，用求得的最优参数进行建模，并对未来的年最大负荷进行预测。

1 主成分分析

主成分分析（principal component analysis， PCA）是一种用于数据压缩和特征提取的多元统计分析技术，其关键是通过坐标变换将一组存在相关性的原始变量转换为一组互不相关的新变量，使得新变量在维数降低的同时尽可能全地保留原始信息［14-15］。

4 算 例

以某海上油田2011—2019年的年最大负荷、年提液量、年产油量、年产气量、年产水量和年注水量历史数据为例进行分析。年最大负荷预测模型架构如图2所示。

4.1 特征量分析与处理

海上油田井口平台提取的井液经中心平台处理得到油、气、水三相。处理合格后的原油由输油泵经海底管道或游轮输送至陆地终端，分离出的天然气一部分输送至陆地终端，一部分经过压缩后供给平台的燃气轮机使用，分离出的水经由注水泵回注到井口。平台液、油、气、水的产量决定了相关电气设备的使用情况，影响电力负荷需求。

在油田开发前期油层本身的弹性能量足以使地层原油喷到地面，不需要人为补充能量。随着采出石油量不断增加，油层压力日益降低，此时需要对油田进行注水以补充地层能量，因此注水量也影响电力负荷需求。5个与油气开采相关的特征量和年最大负荷的变化曲线如图3（图中数值为归一化后的值）所示。

由图3可知，2011—2019年该平台年最大负荷变化较平稳，在2011—2015年期间提液量和产气量逐年升高，产油量较稳定，产水量逐年增多但维持在较低水平，平台处于开发的前中期。在2016—2019年期间产油量大幅度下降，产水量逐渐超过产油量，原油含水率增高，平台已进入开发后期。年注水量整体呈上升趋势，与产油量的变化趋势相反，在油田开发后期地层能量逐渐枯竭，因而注水量增加幅度较大。

由上述分析可知，年最大负荷与油气生产的特征量之间存在复杂的相互联系，油气生产存在减产不减电的特性。计算5个特征量的相关系数，结果如表1所示。

由表1可知，仅产油量与提液量、产气量与产油量之间的相关系数绝对值小于0.5，各特征量之间存在较高的相关性，如果直接用于建立预测模型会导致较大的误差，所以用主成分分析法对特征量进行预处理。首先求出样本协方差矩阵的特征值及相应特征向量，随后根据特征值的累积贡献率选取s个主成分，分别定义第i个特征值的贡献率gi与前s个特征值的累积贡献率G：

式中，λ为样本协方差矩阵的特征值。

计算得到5个特征值、贡献率和累积贡献率如表2所示。

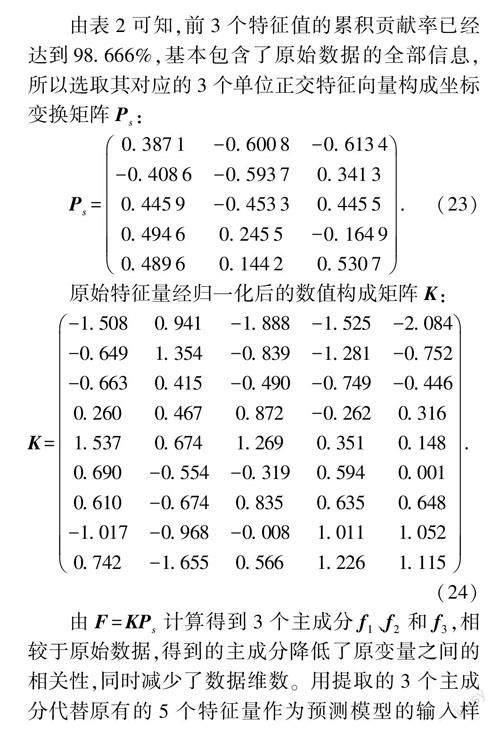
由表2可知，前3个特征值的累积贡献率已经达到98.666%，基本包含了原始数据的全部信息，所以选取其对应的3个单位正交特征向量构成坐标变换矩阵Ps：

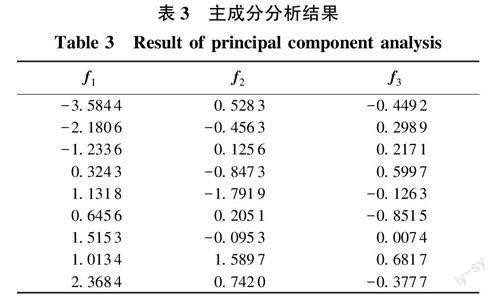
由F=KPs计算得到3个主成分f1、f2和f3，相较于原始数据，得到的主成分降低了原变量之间的相关性，同时减少了数据维数。用提取的3个主成分代替原有的5个特征量作为预测模型的输入样本，其数值如表3所示。

4.2 年最大负荷预测模型建立

根据历史数据计算各主成分与年最大负荷之间的灰色关联度及相应权重，结果如表4所示。

建立各主成分与最大负荷的一元局部加权回归模型，分别得到1，2，3，根据表4中相应权重应用式（20）求得最终预测值。设定粒子群算法参数如下：粒子种群规模50，最大迭代次数Jmax为200，学习因子c1=c2=1.5，最大惯性权重ωmax=0.8，最小惯性权重ωmin=0.4，限定参数k的取值范围为0.5～4，最终求得k=3.3。k分别为0.5、1.0、1.5、2.0、2.5和3.3时，预测结果的均方根误差分别为100.400、65.227、51.024、47.341、46.674和46.555 kW。

当k取值较小时，RMSE较大，预测效果差；当k逐渐增大时，RMSE开始减小，当接近最优值3.3时，不同k下的RMSE十分接近。在选取相同历史数据与建模参数的情况下，将所提方法与其他方法进行比较，选取相对误差ER与平均绝对百分误差EMAPE作为评价指标，二者表达式分别为

3种方法的校验结果对比如表5所示。

由表5可知，3种方法中用主成分分析处理特征量后采用多元线性回归模型的方法精度最低；未进行特征量处理而直接采用基于灰色关联度的局部加权回归模型的方法精度较高；在此基础上增加主成分分析对特征量的预处理使精度进一步提高。结果证明所提负荷预测方法有效。使用经粒子群算法求解得到的k，用2011—2019年的历史数据建模，对海上油田未来10 a的年最大负荷进行预测，2020—2029年最大负荷预测值分别为2 569、2 562、2 566、2 569、2 570、2 571、2 572、2 572、2 573和2 574 kW。

预测未来10 a的最大负荷变化幅度较小，这与相关特征量的预测数值变化较平缓是一致的。

5 结 论

（1）主成分分析法可以对多变量进行降维，同时减小变量之间的相关性，与直接建模相比较，用处理后的特征量建模可以进一步提高预测精度。

（2）根据主成分与最大负荷之间的关联度确定回归结果的权重，同时用粒子群算法对局部加权回归的中间参数进行优化求解，有效提高了中长期负荷预测精度。

参考文献：

［1］李雪，张安安，敬佳佳，等.海上平台电力系统研究综述［J］.电网与清洁能源，2016，32（2）：1-7.

LI Xue， ZHANG Anan， JING Jiajia， et al. Overview of offshore electric systems［J］. Power System and Clean Energy， 2016，32（2）：1-7.

［2］康重庆，夏清，张伯明.电力系统负荷预测研究综述与发展方向的探讨［J］.电力系统自动化，2004，28（17）：1-11.

KANG Chongqing， XIA Qing， ZHANG Boming. Review of power system load forecasting and its development［J］. Automation of Electric Power Systems， 2004，28（17）：1-11.

［3］LI Y Y， HAN D， YAN Z. Long-term system load forecasting based on data-driven linear clustering method［J］. Journal of Modern Power Systems and Clean Energy， 2018，6（2）：306-316.

［4］刘升伟，王星华，鲁迪，等.基于改进高斯过程回归的短期负荷概率区间预测方法［J］.电力系统保护与控制，2020，48（1）：18-25.

LIU Shengwei， WANG Xinghua， LU Di， et al. Electric load probabilistic interval prediction method based on improved Gaussian process regression ［J］. Power System Protection and Control， 2020，48（1）：18-25.

［5］韦钢，贺静，张一尘.中长期电力负荷预测的盲数回归方法［J］.高电压技术，2005，31（2）：73-75.

WEI Gang， HE Jing， ZHANG Yichen. Application of the unascertained number in the improvement of the regressive load forecasting model［J］. High Voltage Engineering， 2005，31（2）：73-75.

［6］王艳松，赵惺，李强，等.基于油气开采的海上油田中长期电力负荷预测［J］.中国石油大学学报（自然科学版），2021，45（2）：127-133.

WANG Yansong， ZHAO Xing， LI Qiang， et al. Medium and long term power load prediction of offshore oil field based on oil and gas exploitation［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2021，45（2）：127-133．

［7］陈先飞，何山，王杰，等.基于MGM（1，n，r）的主动配电网中长期负荷预测［J］.太阳能学报，2020，41（2）：188-193.

CHEN Xianfei， HE Shan， WANG Jie， et al. Mid-long term load forecasting of active distribution network based on MGM（1，n，r）［J］. Acta Energiae Solaris Sinica， 2020，41（2）：188-193.

［8］張红，袁铁江，谭捷.统一能源系统氢负荷中长期预测［J］.中国电机工程学报，2021，41（10）：3364-3372，3662.

ZHANG Hong， YUAN Tiejiang， TAN Jie. Medium and long-term forecast of hydrogen load in unified energy system［J］. Proceedings of the CSEE， 2021，41（10）：3364-3372，3662.

［9］叶莉莉，谢乃明，罗党.累积时滞非线性ATNDGM（1，N）模型构建及应用［J］.系统工程理论与实践，2021，41（9）：2414-2427.

YE Lili， XIE Naiming， LUO Dang. Construction of accumulative time-delay nonlinear ATNDGM（1，N） model and its application［J］. Systems Engineering：Theory & Practice， 2021，41（9）：2414-2427.

［10］王寧，谢敏，邓佳梁，等.基于支持向量机回归组合模型的中长期降温负荷预测［J］.电力系统保护与控制，2016，44（3）：92-97.

WANG Ning， XIE Min， DENG Jialiang， et al. Mid-long term temperature-lowering load forecasting based on combination of support vector machine and multiple regression［J］. Power System Protection and Control， 2016，44（3）：92-97.

［11］肖其师，刘哲.基于神经网络分位数回归的上海市长期用电负荷预测［J］.合肥工业大学学报（社会科学版），2019，33（3）：13-17.

XIAO Qishi， LIU Zhe. Long-term forecast of power load in Shanghai based on quantile regression neural network［J］. Journal of Hefei University of Technology （Social Sciences）， 2019，33（3）：13-17.

［12］FAN G F， QING S， WANG H， et al. Support vector regression model based on empirical mode decomposition and auto regression for electric load forecasting［J］. Energies， 2013，6（4）：1887-1901.

［13］刘明，王红蕾，索良泽.基于变权组合模型的中长期负荷概率密度预测［J］.电力系统及其自动化学报，2019，31（7）：88-94.

LIU Ming， WANG Honglei， SUO Liangze. Medium and long-term load probability density forecasting based on variable weight combination model［J］. Proceedings of the CSU-EPSA， 2019，31（7）：88-94.

［14］王依宁，解大，王西田，等.基于PCA-LSTM模型的风电机网相互作用预测［J］.中国电机工程学报，2019，39（14）：4070-4081.

WANG Yining， XIE Da， WANG Xitian， et al. Prediction of interaction between grid and wind farms based on PCA-LSTM model［J］. Proceedings of the CSEE， 2019，39（14）：4070-4081.

［15］陈修，徐守余，李顺明，等.基于支持向量机和主成分分析的辫状河储层夹层识别［J］.中国石油大学学报（自然科学版），2021，45（4）：22-31.

CHEN Xiu， XU Shouyu， LI Shunming， et al. Identification of interlayers in braided river reservoir based on support vector machine and principal component analysis［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2021，45（4）：22-31．

［16］赵佩，代业明.基于实时电价和加权灰色关联投影的SVM电力负荷预测［J］.电网技术，2020，44（4）：1325-1332.

ZHAO Pei， DAI Yeming. Power load forecasting of SVM based on real-time price and weighted grey relational projection algorithm［J］. Power System Technology， 2020，44（4）：1325-1332.

［17］MUDDINENI V P， BONALA A K， SANDEPUDI S R. Grey relational analysis-based objective function optimization for predictive torque control of induction machine［J］. IEEE Transactions on Industry Applications， 2021，57（1）：835-844.

（编辑 沈玉英）

收稿日期：2022-07-28

基金项目：国家重点研发计划（2018YFB0904800）

第一作者：王艳松（1965-），女，教授，博士，研究方向为电力负荷预测、综合能源规划与运行控制、配电自动化等。E-mail： wys@upc.edu.cn。

通信作者：申晓阳（1998-），男，硕士研究生，研究方向为电力负荷预测。E-mail： s20150051@s.upc.edu.cn。