融合机制与高斯混合回归算法的成品油管道顺序输送混油长度预测模型

袁子云　刘刚　陈雷　邵伟明　张钰晗

摘要：成品油管道順序输送过程中会出现混油现象，精确预测混油长度对油品批次切割具有重要意义，混油长度机制模型存在精度不高，数值计算量庞杂等问题。当前基于机器学习算法构建的全局预测模型未考虑实际工况多模态特性，预测精度受限；直接引入高斯混合回归算法辨识数据模态难以准确表征变量间复杂非线性关系。采用现有机制计算公式与高斯混合回归算法构建融合机制认知的局部建模算法，基于真实成品油管道顺序输送混油长度数据集进行不同模型预测结果对比试验。结果表明，融合机制认知与局部建模算法能有效表征变量间函数关系，新模型预测精度有明显优势。

关键词：成品油管道； 混油长度； 局部建模； 高斯混合回归； 机制-数据

中图分类号：TP 181 文献标志码：A

引用格式：袁子云，刘刚，陈雷，等.融合机制与高斯混合回归算法的成品油管道顺序输送混油长度预测模型［J］.中国石油大学学报（自然科学版），2023，47（2）：123-128.

YUAN Ziyun， LIU Gang， CHEN Lei， et al. Predictive model of mixed oil length for sequential transportation of multi-product pipeline by combining mechanism and Gaussian mixture regression algorithm ［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2023，47（2）：123-128.

Predictive model of mixed oil length for sequential transportation of multi-product pipeline by combining mechanism and

Gaussian mixture regression algorithm

YUAN Ziyun1，2 ， LIU Gang1，2， CHEN Lei1，2， SHAO Weiming2，  ZHANG Yuhan3

（1.College of Pipeline and Civil Engineering in China University of Petroleum（East China），  Qingdao 266580， China;2.Shandong Provincial Key Laboratory of Oil & Gas Storage and Transportation Safety， Qingdao 266580， China; 3.Qingdao Operation Area， Shandong Branch， PipeChina，  Qingdao 266400， China）

Abstract： The oil mixing phenomenon  occurs during the sequential transportation of the multi-product pipeline， and the accurate prediction of the length of the mixed oil is of great significance for the cutting batch segment. The mechanism model is faced with problems such as low accuracy and complex numerical simulation. In the current global predictive models derived from machine learning algorithms， the multi-mode characteristics of actual operating conditions are ignored， thus the predictive accuracy is limited. The Gaussian mixture regression algorithm cannot accurately characterize the complex nonlinear relationship among variables if it is directly introduced to identify the data mode. Based on the existing mechanism equation and the Gaussian mixture regression algorithm， we develop a local modeling algorithm that integrates the mechanism knowledge. Based on the real product oil pipeline sequential transportation mixed oil length data set， a comparison experiment  among different models was carried out， and the results show that the mechanism and local modeling algorithm can effectively characterize the functional relationship of variables， and the predictive accuracy of the new model has obvious advantages.

Keywords： multi-product pipeline; mixed oil length; local modeling; Gaussian mixture regression; mechanism-data

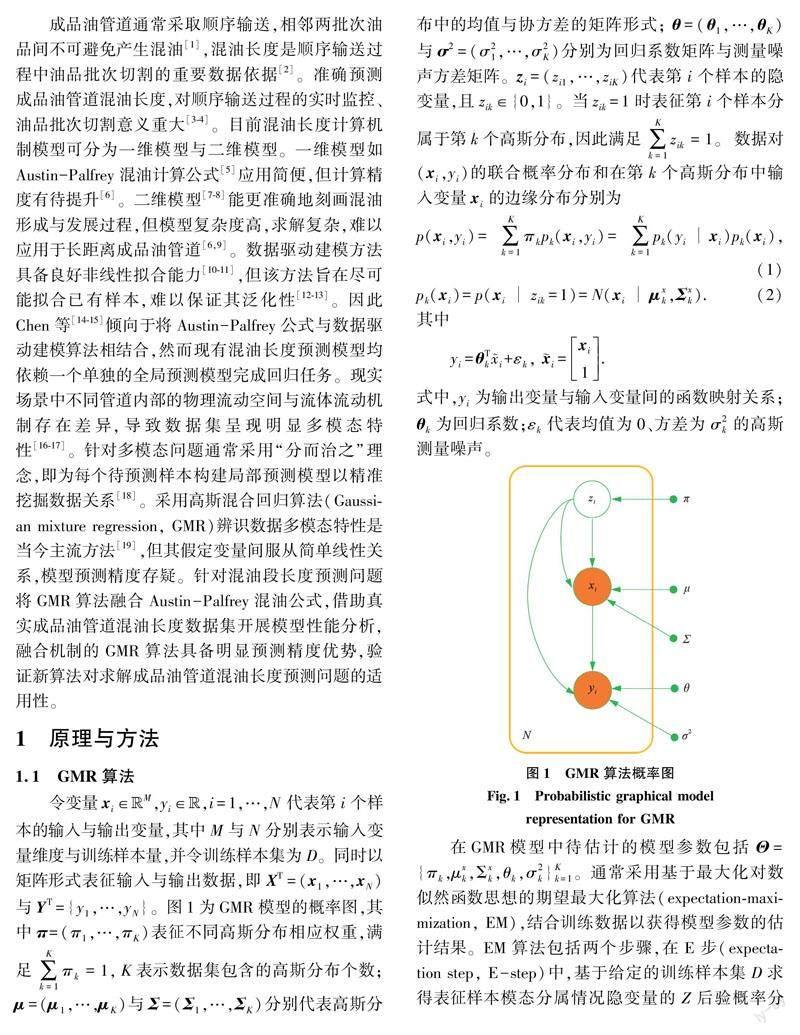
成品油管道通常采取顺序输送，相邻两批次油品间不可避免产生混油［1］，混油长度是顺序输送过程中油品批次切割的重要数据依据［2］。准确预测成品油管道混油长度，对顺序输送过程的实时监控、油品批次切割意义重大［3-4］。目前混油长度计算机制模型可分为一维模型与二维模型。一维模型如Austin-Palfrey混油计算公式［5］应用简便，但计算精度有待提升［6］。二维模型［7-8］能更准确地刻画混油形成与发展过程，但模型复杂度高，求解复杂，难以应用于长距离成品油管道［6，9］。数据驱动建模方法具备良好非线性拟合能力［10-11］，但该方法旨在尽可能拟合已有样本，难以保证其泛化性［12-13］。因此Chen等［14-15］倾向于将Austin-Palfrey公式与数据驱动建模算法相结合，然而现有混油长度预测模型均依赖一个单独的全局预测模型完成回归任务。现实场景中不同管道内部的物理流动空间与流体流动机制存在差异，导致数据集呈现明显多模态特性［16-17］。针对多模态问题通常采用“分而治之”理念，即为每个待预测样本构建局部预测模型以精准挖掘数据关系［18］。采用高斯混合回归算法（Gaussian mixture regression， GMR）辨识数据多模态特性是当今主流方法［19］，但其假定变量间服从简单线性关系，模型预测精度存疑。针对混油段长度预测问题将GMR算法融合Austin-Palfrey混油公式，借助真实成品油管道混油长度数据集开展模型性能分析，融合机制的GMR算法具备明显预测精度优势，验证新算法对求解成品油管道混油长度预测问题的适用性。

1 原理与方法

1.3 融合机制公式与GMR算法的GMR－M模型

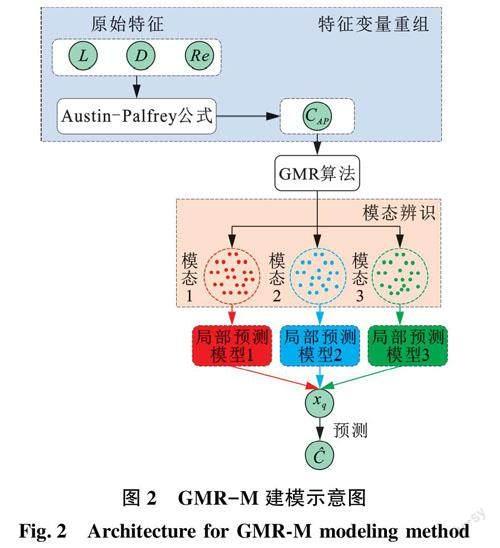
在GMR模型中假定第k个模态内输入输出变量间的函数关系为简单的线性关系。因成品油管道顺序输送过程受多因素耦合影响，且流体流动状态复杂多变，输入输出变量间应服从复杂非线性关系，完全基于GMR算法构建的预测模型将难以准确描述混油长度发展规律。因此考虑结合GMR算法与已有机制公式，将多维输入变量与对应输出变量间的复杂非线性关系简化为线性关系，再利用GMR算法辨识数据间隐含的多模态关系，在同一模态下构建局部预测模型，实现预测精度的有效提升。GMR-M建模具体流程如下，相应示意图见图2。

（1）基于式（5），将管道内径d、输送距离L以及运行雷诺数Re整合成变量CAP。

（2）结合GMR算法探寻不同模态条件下输入变量CAP与输出变量即混油长度C间的函数关系。

（3）输入待预测样本xq可预测相应混油长度预测值。

考虑到人工神经网络作为数据分析领域主流算法之一［21-22］及其对复杂非线性函数的优秀拟合能力，选择其为对照方法以验证GMR-M模型在混油长度预测问题上的优越性。此外为说明融合机制公式与考虑数据多模态特点的重要性，基于变量重组方式构建了ANN-M模型。相较于GMR-M模型，基于人工神经网络算法的ANN-M模型并未辨识数据多模态信息。单纯基于GMR，ANN构建的预测模型的输入变量信息为L、d、Re；GMR-M和ANN-M的输入变量信息为CAP。

2 实 例

采用真实混油长度数据集以验证GMR-M模型的适用性，以Austin-Palfrey公式，现有两种预测模型以及单纯基于GMR，ANN算法构建模型与ANN-M模型的预测结果作为基准，对比分析GMR-M模型在预测精度方面的表现。其中GMR-M与GMR模型模态数均设置为3，ANN与ANN-M隐藏层神经元个数设置为10。主要采用均方根误差（root mean square error， RMSE）、最大绝对误差（max absolute error， MAE）与决定系数R2作为评价模型的预测性能指标，评价指标分别为

式中，ERMS和EMA分别为均方根误差和最大绝对误差；yq、q与q分别为样本实际值、预测值与样本均值；Q为测试样本数量。

R2指标越大，表明预测值与实际值吻合程度更高。而RMSE与MAE指标越大，代表预测结果越偏离实际值。利用SCADA（supervisory control and data acquisition）系统采集的中国南方三条成品油管道生产运行数据作为样本来源，部分样本基本信息如表1所示。

前两条管道共计1 948个样本用于训练模型，第三条管道中528个样本用于构建测试数据集以评估不同预测模型的泛化性能。各模型相应预测指标列于表2。

由表2可知，对于现有预测模型，Chen模型的RMSE指标已超过Austin-Palfrey公式的预测结果，表明该模型预测值拟合样本实际值效果不佳。虽然Yuan模型表现出相对较优的预测性能，但未考虑数据多模态特性仍导致其出现预测失真，相比于现有机制计算公式难以显现出明显预测优势。由于神经网络具备复杂非线性拟合能力，ANN与ANN-M模型在混油长度预测问题上表现出较好的预测能力。从整体来看，二者的決定系数R2超过0.94，模型预测结果与实际值较为接近。相较于现有两种预测模型，基于ANN算法构建的预测模型具备一定优势。此外相较于ANN模型，基于已有计算公式重组输入变量得到的ANN-M能更精确捕捉变量间的函数映射关系，预测性能有一定的提升。但其MAE指标均约为900且超过了现有两种预测模型，说明基于神经网络构建的预测模型对个别样本出现了较严重的预测偏差，模型预测能力仍有待提升。可知，因忽略数据集内样本可能来源于不同模态导致变量间函数关系存在的差异，即使融合已有机制公式并采用具备拟合非线性能力的数据分析算法，全局建模方法预测分属不同模态样本时适用性仍欠佳，导致预测结果偏离实际情况。

对比GMR模型，由于未有机结合已有机制公式，模型无法有效表征输入变量与输出变量间的复杂非线性关系，预测结果不理想。反映在GMR表现出最高的RMSE和MAE指标，说明直接引入GMR算法难以解决混油长度预测问题。与之相对的，融合了机制表达形式且采用局部建模方法的GMR-M模型，预测结果更贴近真实情况。GMR-M模型的RMSE与R2预测指标均明显优于其他模型。具体而言，GMR-M是RMSE指标唯一低于200的模型，且表现出最低的MAE指标，充分表明GMR-M具备良好的预测精度。上述结果有效验证了融合机制公式与局部建模方法在准确预测成品油管道顺序输送混油长度预测问题中的重要性。

图3为各模型估计值与测试集样本实际值的拟合情况。由图3可以看到，相较于混油长度实际值，基于Austin-Palfrey公式得到的预测值偏低；因缺少模态识别步骤，Chen-和Yuan模型表现出明显的预测偏差；单纯基于GMR算法构建的预测模型，由于未有机融合机制公式，导致模型陷入过拟合，预测精度不理想；ANN和ANN-M预测值较接近实际值，然而融合了机制公式与多模态识别功能的GMR-M模型表现出最高的预测精度，预测值拟合实际值效果最好，表明模型精准捕捉到了输入输出变量间的函数映射关系。

3 结束语

为克服现有成品油管道顺序输送混油长度预测方法中存在的不足，提出了一种融合机制与GMR算法的成品油管道混油长度预测模型GMR-M。与现有预测模型以及ANN模型相比，因考虑了数据内部多模态特性并针对性地构建了多个局部预测模型完成回归任务，GMR-M模型能有效提高成品油管道混油长度预测精度；对比已有机制公式与单纯采用GMR算法构建的预测模型，通过耦合现场数据携带的关键信息与已有机制认知，GMR-M模型能更有效表征输入输出变量间的复杂函数关系，预测结果更接近于真实情况。

参考文献：

［1］HE Guoxi， LIN Mohan， WANG Baoying， et al. Experimental and numerical research on the axial and radial concentration distribution feature of miscible fluid interfacial mixing process in products pipeline for industrial applications［J］. International Journal of Heat & Mass Transfer， 2018，127：728-745.

［2］SHAHANDEH H， LI Z. Modeling and optimization of the upgrading and blending operations of oil sands Bitumen［J］. Energy & Fuels， 2016，30（JUL.SPEC.）：5202-5213.

［3］MORADI S， MIRHASSANI S A. Robust scheduling for multi-product pipelines under demand uncertainty［J］. The International Journal of Advanced Manufacturing Technology， 2016，87（9）：2541-2549.

［4］CAFARO V G， CAFARO D C， MNDEZ CA. Optimization model for the detailed scheduling of multi-source pipelines［J］. Computers & Industrial Engineering， 2015，88：395-409.

［5］AUSTIN J E，PALFREY J R. Mixing of miscible but dissimilar liquids in serial flow in a pipeline［J］. P Mech Eng B-J Eng， 1963，178：377-389.

［6］孙健飞，梁永图.成品油管道顺序输送混油模型研究进展［J］.油气储运，2019，38（5）：496-502.

SUN Jianfei， LIANG Yongtu. Research progress on the mixed oil models for the batch transportation in products pipeline ［J］. Oil & Gas Storage and Transportation， 2019，38（5）：496-502.

［7］夏增艳，刘青泉.顺序输送混油过程的二维数值分析［J］.力学与实践，2010，32（6）：13-17.

XIA Zengyan， LIU Qingquan. Numerical simulation of the contamination between batches in multi-product pipeline transport ［J］. Mechanics in Engineering， 2010，32（6）：13-17.

［8］馬钢，白瑞.成品油管道二维混油理论数值分析研究［J］.油气田地面工程，2018，37（7）：54-59.

MA Gang， BAI Rui. Study on the two-dimensional mixed oil theory numerical analysis for product oil pipelines ［J］. Oil-Gas Field Surface Engineering， 2018，37（7）：54-59.

［9］吳玉国.冷热原油顺序输送技术研究［D］.青岛：中国石油大学（华东），2010.

WU Yuguo. Research on technology of the batch transportation of cold and hot crude oils ［D］. Qingdao：China University of Petroleum（East China） ，2010.

［10］何玉荣，宋志超，张燕明，等.机器学习在水力压裂作业中的应用综述［J］.中国石油大学学报（自然科学版），2021，45（6）：127-135.

HE Yurong， SONG Zhichao， ZHANG Yanming， et al. Review on application of machine learning in hydraulic fracturing ［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2021，45（6）：127-135.

［11］王艳松，赵惺，李强，等.基于油气开采的海上油田中长期电力负荷预测［J］.中国石油大学学报（自然科学版），2021，45（2）：127-133.

WANG Yansong， ZHAO Xing， LI Qiang， et al. Medium and long term power load prediction of offshore oil field based on oil and gas exploitation ［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2021，45（2）：127-133.

［12］张黎明，陈昕晟，李国欣，等.基于集合和神经网络架构搜索的自动历史拟合方法［J］.中国石油大学学报（自然科学版），2022，46（2）：127-136.

ZHANG Liming， CHEN Xinsheng， LI Guoxin， et al. An automatic history matching method based on ensemble and neural architecture search ［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2022，46（2）：127-136.

［13］潘少伟，王朝阳，张允，等.基于长短期记忆神经网络补全测井曲线和混合优化XGBoost的岩性识别［J］.中国石油大学学报（自然科学版），2022，46（3）：62-71.

PAN Shaowei， WANG Chaoyang， ZHANG Yun， et al. Lithology identification based on LSTM neural networks completing log and hybrid optimized XGBoost ［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2022，46（3）：62-71.

［14］CHEN L， YUAN Z Y， LIU G， et al. A novel predictive model of mixed oil length of products pipeline driven by traditional model and data［J］. Journal of Petroleum Science and Engineering，2021，205：108787.

［15］YUAN Z Y， CHEN L， SHAO W M， et al. A robust hybrid predictive model of mixed oil length with deep integration of mechanism and data［J］. Journal of Pipeline Science and Engineering， 2021，1（4）：459-467.

［16］SOUZA F， RUI A. Mixture of partial least squares experts and application in prediction settings with multiple operating modes［J］. Chemometrics and Intelligent Laboratory Systems， 2013，130（2）：192-202.

［17］SHAO W， GE Z， SONG Z. Soft-sensor development for processes with multiple operating modes based on semisupervised Gaussian mixture regression［J］. IEEE Transactions on Control Systems Technology， 2019，27（5）：2169-2181.

［18］SHAO W， GE Z， SONG Z， et al. Data-driven predictive model based on locally weighted Bayesian Gaussian Regression：  2019 IEEE 8th Data Driven Control and Learning Systems Conference （DDCLS）［C］. Dali： IEEE， 2019.

［19］WANG J， SHAO W， SONG Z. Bayesian regularized Gaussian mixture regression with application to soft sensor modeling for multi-mode industrial processes：2018 IEEE 7th Data Driven Control and Learning Systems Conference （DDCLS）［C］. Enshi： IEEE， 2018.

［20］SHAO W， XIAO C， WANG J， et al. Real-time estimation of quality-related variable for dynamic and non-Gaussian process based on semisupervised Bayesian HMM［J］. Journal of Process Control， 2022，111：59-74.

［21］宋先知，朱碩，李根生，等.基于BP-LSTM双输入网络的大钩载荷与转盘扭矩预测［J］.中国石油大学学报（自然科学版），2022，46（2）：76-84.

SONG Xianzhi， ZHU Shuo， LI Gensheng， et al. Prediction of hook load and rotary drive torque during well-drilling using a BP-LSTM network［J］. Journal of China University of Petroleum（Edition of Natural Science），2022，46（2）：76-84.

［22］郑秋梅，商振浩，王风华，等.基于深度神经网络和支持向量机的海底管线水合物生成预测模型［J］.中国石油大学学报（自然科学版），2020，44（5）：46-51.

ZHENG Qiumei， SHANG Zhenhao， WANG Fenghua， et al. Prediction model of submarine pipeline hydrate formation based on deep neural network and support vector machines［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2020，44（5）：46-51.

（编辑 沈玉英）

收稿日期：2022-08-12

基金项目：国家重点研发计划（2021YFA1000104）；国家自然科学基金项目（52174068）；中央高校自主创新基金项目（22CX01001A-5）

第一作者：袁子云（1998-），男，博士研究生，研究方向为油气管网大数据分析。E-mail：yuanziyun@s.upc.edu.cn。

通信作者：刘刚（1975-），男，教授，博士，博士生导师，研究方向为油气管道系统数据挖掘与智能决策的应用。E-mail：liugang@upc.edu.cn。