索道吊具的偏心设计与平衡计算

马 胤 姜红旗

北京起重运输机械设计研究院有限公司 北京 100007

0 引言

在计算平衡状态时，常用的方法包括作图法和合重心法。作图法是最常用的方法之一，它需要将吊具各部分的重心位置和质量估算为质点，并通过反复作图来找到平衡状态下的摆角。这个方法直观但繁琐，特别是在考虑多种工况时需要进行大量的作图计算。合重心法通过计算各部分重心的合成重心确定不同工况下的摆角，通过合重心计算公式，可以得出各工况下吊具的合重心坐标，并取其摆角作为平衡状态的摆角。这种方法更适合考虑多种工况，可以精确地找出吊具的偏摆角度。

为了优化吊具的摆动量，可以使用变量参数和合重心法。通过引入设计偏心值作为变量，可以通过解析的方式找到最合理的设计偏心值。同时，通过列出各个物体的质量和重心坐标，并利用合重心公式，可以计算出不同工况下的合重心坐标，并取其摆角作为吊具的理论平衡摆动角度。

索道吊具的偏心设计与平衡计算是一个复杂的问题，可以通过作图法和合重心法来进行计算。合重心法可以更精确地确定吊具的平衡状态，并通过引入变量参数来优化吊具的设计偏心值。这些方法对于提高吊具的稳定性和乘客的乘坐感受非常重要。

1 计算平衡状态的方法

1.1 作图法

作图法是在设计吊具与吊杆偏心的过程中为最常用的方法，需要提前获知或估算出吊具各部分的重心位置与质量，可以把各组成部分简化为质点来考虑，图1 所示为吊具各组成部分的重心简化图。该图为最常见吊具的情况，即吊杆与吊具固定连接，不考虑各部分形变，可认为两者绕钢丝绳旋转时的摆动角度相同。

图1 吊具重心简化图

作图法首先需要画出理想状态下各部分的重心位置。图1a 为理想状态下的吊具状态，其不是吊具的满载或空载的自然平衡状态。这是由于吊具一般单侧有门(图示吊厢右侧黑线)导致其重心相对自身的中心有一小偏心Ld。图中Lp表示设计偏心值，即所探讨的偏心距离对象。设计偏心的选取原则应使整体吊具系统在空载与满载的情况下摆角近似相同，同时尽量保证两者摆角之和最小，即θ'≈θ''且min(θ'+θ'')。

在绘制平衡图时，整个系统按照以钢丝绳为中心旋转进行考虑(不考虑钢丝绳的扭转刚度)。在空载时，钢丝绳左侧的重力矩之和(即抱索器重力矩与吊杆重力矩之和)一般大于钢丝绳右侧的重力矩之和(空厢重力矩)，为了找到空载状态下吊具的平衡角度，可先将整体逆时针旋转一角度θ'后作图(见图1b)，测量各部分新位置的重心到钢丝绳水平距离的分量，即Lxb'、Lxg'、Lxd'，然后分别乘以各自部分的质量，将钢丝绳左右各部分的重力矩之和进行比较，如果钢丝绳左侧重力矩仍大于右侧重力矩，则继续逆时针旋转作图，直到左右重力矩近乎相同，取该状态的摆角θ'，即为吊具系统在空载时平衡状态的摆角。

在满载时，由于人的质量影响，一般钢丝绳右侧的重力矩大于左侧的重力矩，整个系统需要顺时针旋转才能达到平衡。在计算承载人员时，可以将左右两侧的乘客分别考虑（见图1c），也可以将承载人员的重力作为一个整体简化考虑，作用于吊厢对称中心线上（需要注意的是简化考虑并不十分精确，因为实际上半载乘客只坐在吊厢的一侧时，偏转角度可能进一步增大），具体过程不再赘述。

在通常情况下，由于带载情况下系统的总质量增加，使得吊具更不容易发生偏摆，即带载吊具的平衡状态更加稳定，摆动角度一般相对于空载时更小。这在受到风载和其他作用时对满载吊具的影响比空载吊具要小，并且载荷越大，整体平衡偏转角度越小。

然而，该作图方法需要进行反复的作图迭代计算，尽管直观，但相对繁琐，尤其在不确定乘客载荷位置的不同工况下，需要进行大量的作图核算工作。为了提高效率和准确性，在设计吊具时可能需要借助计算机辅助设计软件辅助进行计算和模拟分析，以减少繁琐的手工作图过程，提高设计的精确性和效率。

1.2 合重心法

对于多个物体的平衡计算也可以通过计算其合重心的方法确定不同工况下的摆角。合重心计算时无需进行摆动作图，只需将不同工况下的各部分的重心位置在理想状态图上全部表示出来即可。

根据合重心的计算公式，假设有3 个物体A、B 和C，其质量分别为M1、M2和M3，物体重心的坐标分别为G1(X1，Y1)，G2(X2，Y2)，G3(X3，Y3)，则吊具整体系统合重心的X坐标为

吊具整体系统合重心的Y坐标为

如图1 所示，以钢丝绳中心为原点建立坐标系，水平向右方向作为x轴，垂直向下方向作为y轴，列出或估算出各种工况下各物体的重心点位置坐标，包括抱索器重心坐标、吊杆重心坐标、吊厢重心坐标和乘客重心坐标等。然后，通过上述公式分别求出不同工况下吊具系统合重心的X及Y坐标值。(X/Y)取arctan(X/Y)即可得到不同工况下吊具的理论静态平衡时的摆动角度。

相比于作图法，合重心法可以非常精确地计算出吊具的理论静态平衡角度，省去了重复作图的工作，并且更适用于多种工况的考虑。在计算过程中，只需根据实际运行情况考虑包括或排除人载荷部分的重心影响，就可以获得不同工况下的合重心位置和平衡摆动角度。

另外，作图法虽然更精确，但对于吊具系统整体最优的偏摆距离选择不够直观，其只能求出不同工况下的合重心位置与相应的摆动平衡角度，却不能体现出偏心距离的选取对不同工况下摆动量的影响。

2 基于合重心法的优化方法

2.1 变量参数

为了使吊具在各种工况下的摆动量尽可能小，需要找到最合理的设计偏心值。通过作图法几乎不可能实现这一目标，且每选取一个设计偏心值都需要进行摆动作图，工作量巨大。然而，结合合重心法并通过定义变量来进行解析吊具的摆动问题，有助于找出最合理的设计偏心值。

以某个4 人抱索器吊厢的偏心设计计算为例，首先需要绘制出全工况下各部分的理想状态重心位置图(见图2)。假设设计偏心值为变量Lp，已知抱索器质量Mb和抱索器重心坐标Gb。由于偏心值的选取直接影响吊杆的质量与其重心的位置，所以先估算吊杆质量为Mg，并估算吊杆的大致重心坐标为Gg。已知吊厢质量为Md，吊厢重心坐标为Gd，可以通过设计偏心值Lp导出其坐标x(Gd)，y坐标y(Gd)亦可以直接估算出来。

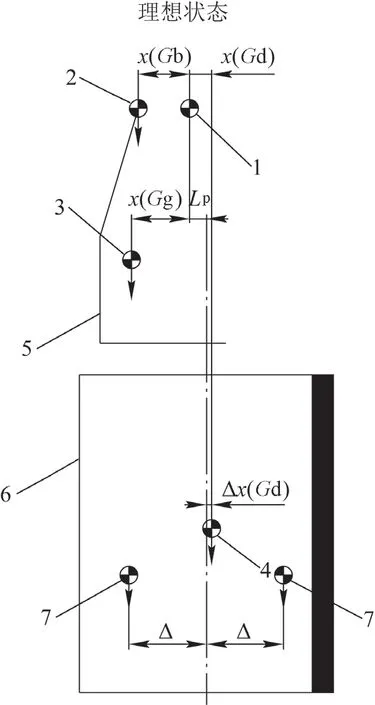
图2 全局工况下的理想重心图

吊厢的重心x坐标为

已知乘客质量为Mr，乘客重心坐标为Gr。Gr可以通过设计偏心值Lp导出其坐标x(Gr)和y(Gr)。乘客距离吊厢中心的偏心值可以估算为Δ。

吊厢左侧乘客重心x坐标为

吊厢右侧乘客重心x坐标为

控制系统变量，定义抱索器质量为Mb，坐标为Gb。吊杆质量为Mg，坐标为Gg。吊厢质量为Md，坐标为Gd。人(左) 质量为Mr，坐标为GrL。人(右) 质量为Mr，坐标为GrR。

以上参数的所有物体的质量与重心坐标已知，或可以粗略估算出来。变量只有设计偏心值Lp。然而实际上吊杆的质量和重心位置也是变量，它随着设计偏心值的增大而增大，只是它对整体系统的影响比例一般较小，可以先不进行精确的考虑。当吊杆的质量影响较大时，如质量接近抱索器或吊厢等，在选择设计偏心值后须再次进行平衡摆动角度的校核。

2.2 不同工况的合重心坐标分量表达式

2）半载工况(左右各坐1 名乘客)

3）半载工况(左边座2 名乘客)

4）半载工况(右边座2 名乘客)

5）满载工况(座4 名乘客)

2.3 预处理

在计算以上表达式时，可以借助可视化的数学工具进行实时作图计算，这将节省大量的计算时间。通过可视化工具，可以直观地观察不同参数对系统的影响，从而更快地找到最合理的设计偏心值。

为了简化计算过程，可以近似理解全局工况下的最小摆角之和等同于全局工况下合重心分量的最小x坐标之和。尽管也可以按照arctan(X/Y)进行考虑，但这种方法会严重影响计算和显示速度，故不推荐使用。

通过引入一个新的表达式x(G)，用于表示不同工况下合重心的x坐标之和。在该表达式中，每种工况的x坐标表达式后乘以系数1，代表考虑该种工况的影响。还可以乘以系数0，代表不考虑该种工况的影响。选择不同的系数将导致曲线相应地变化。由于各工况下合重心的x坐标可能位于钢丝绳左侧或右侧，即各工况下合重心x的表达式有正负之分，故取其绝对值。

另外，还可以引入另一个新的表达式x(M)，用于表示空载与满载平衡时x分量的差值。该差值可以帮助找到空载摆角与满载摆角相同时的设计偏心值。通过调整设计偏心值，使空载和满载时的摆角相等，作为在选择吊具偏心值时的参考内容之一。

对于预制混凝土与现浇混凝土之间的模拟，采用两种模型相互结合，即内聚力-库伦摩擦模型.当相对位移较小，面面之间存在黏结作用时，切向应力由内聚力模型提供.随着相对位移的增加，黏结力刚度开始减小，两个模型共同作用提供切向作用力.在对内聚力模型定义时，需要定义法向的弹性刚度Κnn，切向刚度Κss、Κtt；继续定义面面之间的损伤作用[16]，确定法向的峰值应力切向峰值应力损伤启动准则采用最大应力准则，即满足公式(1)，就开始发生损伤.

通过上述扩展和引入新的表达式，可以更深入地分析吊具的设计偏心值问题，并且通过计算和可视化工具来优化计算过程，提高效率。这将有助于更好地设计吊具，减小摆动量，提高工作安全性和效率。x(G)和x(M)表达方式为

2.4 结果分析

在绘制x(G)和x(M)曲线时，x轴为设计偏心值，y轴为全局工况下合重心分量的x坐标之和。上曲线x(G)为各种工况下吊具重心到钢丝绳中心的x分量之和，下曲线x(M)代表空载与满载平衡时合重心的x分量的差值。从上曲线可以观察到，在全局工况下，偏摆的x分量之和存在一个极小值。这意味着接近该点的横坐标取值会使得吊具在所有工况下的摆动角度之和最小。同时，从下曲线可以看出存在一个零点，即说明在空载和满载工况下具有相同摆角的偏心取值存在。因此，在进行吊具的偏心设计时，应该选择接近这2 条曲线上各自最优点的设计偏心值。

然而，在确定设计偏心值之前，需要确定对吊杆质量和重心的估算是否准确。因此，应该在确定设计偏心值之后进行摆动角度的综合考虑。这样可以更精确地评估吊杆的受力情况。

在选择设计偏心值时，还必须考虑吊杆的强度问题。盲目地增大设计偏心值会增加吊杆的应力，故必须优先确保结构的安全强度要求。

通过综合考虑上述影响因素，能够设计出更安全、更稳定的吊具，以满足实际工程需求。同时减小吊具在运行过程中的不确定性，并提高吊具的整体性能和可靠性。

x(G)表达式曲线图如图3 所示。

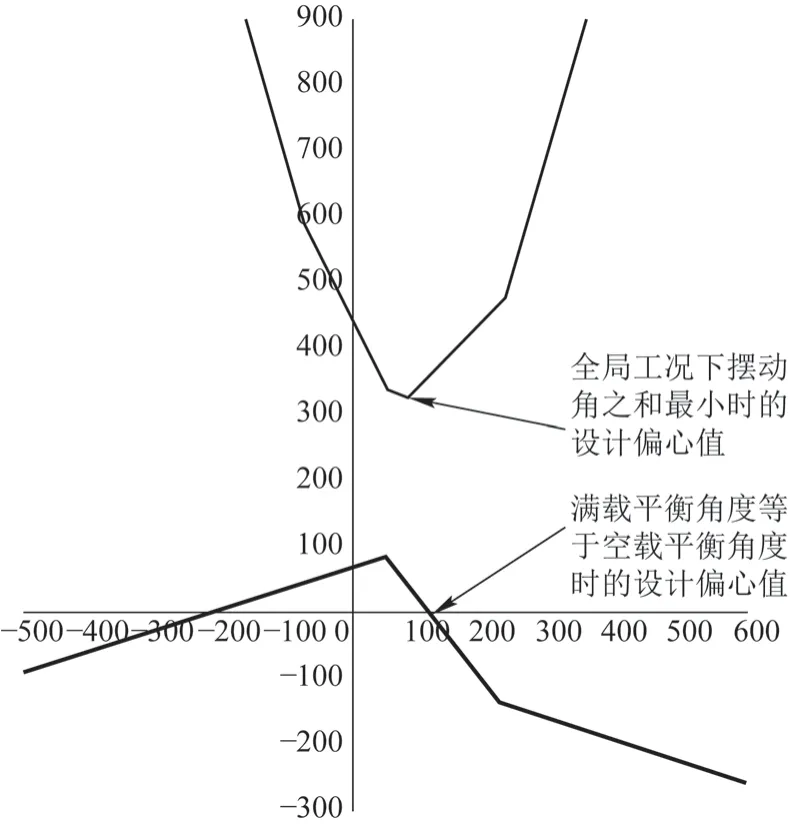
图3 x(G)表达式曲线图

3 探讨与扩展

前文所述的计算方法与过程是在吊具绕钢丝绳自由转动的状态下进行考虑的。实际上，在吊具平衡摆动的过程中，钢丝绳自身的扭转刚度对于吊具自身的平衡摆动也是有一定影响的，当钢丝绳没有释放掉自身的扭转应力时，可能会偏置吊具整体的摆动方向，如增大满载摆动减小反方向空载摆动，抑或相反，其与钢丝绳捻方向，盘绕方向，索道转动方向等有关。而当钢丝绳释放掉了自身扭转应力时，此时的钢丝绳扭转刚度起到抗吊具扭转的效果，能使双方向摆动量减小。

同时，在考虑吊具摆动的问题时，吊架与吊具之间有时并不是刚性连接，往往配置有可活动的阻尼减震装置，使得吊具、吊架和吊杆无法简单看作一整体，3 者之间均存在相对摆动，应引入结构间的阻尼与相对摆动影响，且当运行时整个索道系统的激振与吊具自身的固有频率影响，可能会进一步增加实际摆动量，有待进一步进行研究及探讨。