以学科融合促进学生数学思维的深度发展
2023-09-02吴葆蓉
吴葆蓉
(福建省厦门市新翔小学)
基于深度学习的理论,数学综合实践课程应有意识地培养学生“见解独到、了解深入、抨击怀疑”的思维品质,完成培养学生独立思考的目标。在课堂实践中,教师应始终坚持学科本质为先,聚焦数学思维,深化思维力,以学科融合促进学生的深度学习。本文以人教版数学教材五年级下册“分数的意义”为例进行探讨。
一、融合文学分析,找到思维的起点
在学习分数时,教师应分多阶段进行教学。早在三年级时,学生便接触了分数。而“分数的意义”便是基于之前的知识,使学生深入学习并认知分数,如分数单位、分数的产生、单位“1”的含义,等等。
《义务教育数学课程标准(2022 年版)》(以下通称“新课标”)中提到,学生所学的数学知识应当是有价值的、有意义的。在开展数学学习活动时,除了要考虑学生现有知识经验外,还要兼顾学生的实际认知发展水平。可见,在设计教学时,教师必须做到全面掌握学情。为了解学生对旧知识的掌握情况、对新知识的感知程度以及寻找新旧知识的生长点,笔者设计了一份前测练习,以期更准确地诊断出学生在学习“分数的意义”过程中的难点,并设计出更有针对性的教学方案,提高教学效果。
问题一:下面各图中的涂色部分如果能用分数表示的,请写出相应的分数。


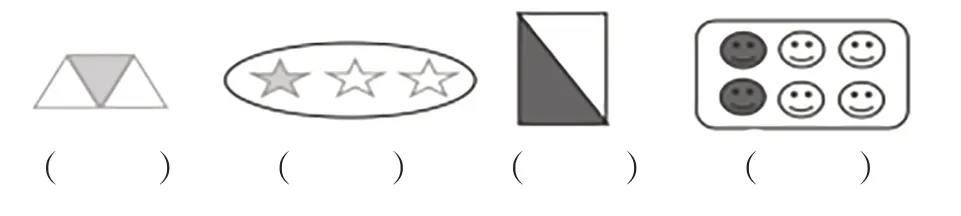
学生对问题一和问题三的完成效果较好,说明他们对于分数已基本掌握。学生在对问题二的描述中基本没有使用“平均分”,也不能完整表述的意思,说明他们还不能准确描述分数的意义。对于问题四,大多数学生只会把一个物体或一个图形平均分成4 份,取其中1 份。仅有3 位学生会用4 个图形平均分成4 份,取1 份。没有学生用多个图形表示,说明学生思维不够丰富。
【分析与思考】
学生通过前测的自我剖析,能明白自己思维的“最近发展区”,为后续新知的学习起点找准方向。不同学生的思维起点不一样,教师精准地把握学情,了解学生对旧知和新知掌握的真实状态,有利于改进教学设计。
二、融合美育辨析,发现思维的本质
在深度学习过程中,学生深度探究活动的开展是一个大项目,教师必须实时关注学生学习的实效性、主动性和策略多样性。教师的设计要关注学生的差异性和多样化学习的倾向,依据学情检测中学生表现出的共性与个性需要及多元智能的要求,让学生会用自己喜欢的方式来表达出自己的理解,并与深层理解达成平衡,最终构建深度的思维模式。
【教学片段一】
师:聪明的古人会用绳子来量一段长度,就像下图这样。我们把一段绳子的长度看作单位“1”,用线段表示。

师:把线段平均分成5 段,每段是这根绳子的多少?
师:那下面这一段是多长呢?
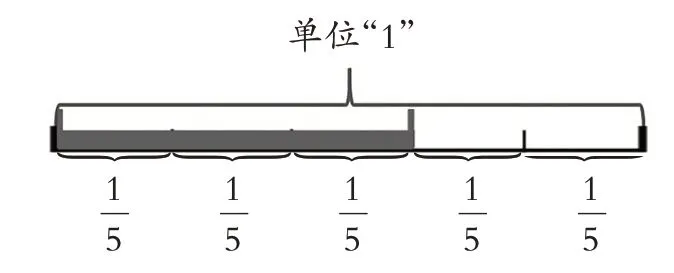
师:你是怎么想的?
师:那下面这两段分别是多长呢?

师:刚才这几个分数都是以什么为计数单位数出来的?
师生小结:单位“1”便是整体,把其分为多份,而分数单位特指其中一份的数。
学生利用已有的知识经验,实现知识迁移,借助“数一数”,从度量的意义上来理解分数单位,理解得更深刻、透彻:分数单位和整数的计数单位一样,一个个分数单位累积形成了更多的分数。教师由整数计数单位过渡到分数单位,使学生更容易把分数单位这一新知识同化到原有的知识结构中。
【分析与思考】
在教师设计好教学方案后,课堂教学便是教学方案的实际再现。在这一环节中,师生互动是少不了的。如此,便会有各种教学资源的生成。鉴于此,教师必须要把控好课堂整体节奏,发挥教育机智,构建高效数学课堂。
三、融合实践分析,聚焦思维进阶
在深度学习的二维纵向横断面中,“深度”展现的是启智增慧、凝心铸魂。深度学习的核心目标是转识成智、由智生慧。教师要聚焦学生“心事”,启发学生思维,设计有利于聚焦思维进阶、任务性强的综合实践活动。
【教学片段二】
问题一:填上合适的分数。
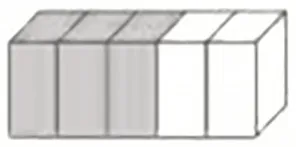
(1)涂色部分是这个长方体的( )

(2)每段是这条线段的( )

(3)每个茶杯是这套茶杯的( )

(4)每次吃的药是这瓶药的( )
问题二:把100颗糖平均分成5份,表示其中的3份的分数是( ),它的分数单位是( ),单位“1”是( )颗糖,其中的1份是( )颗糖。
问题四:猜猜谁的萝卜多?
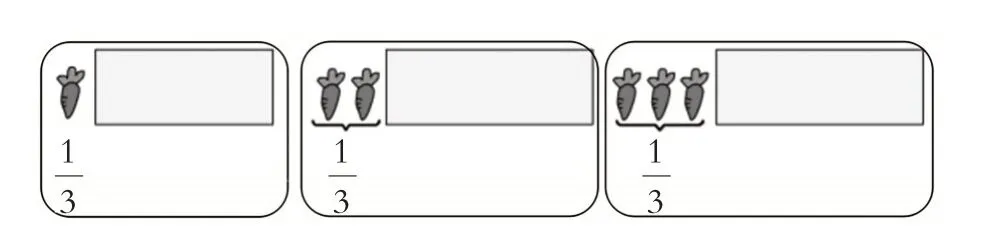
【分析与思考】
在结束授课后,教师应复盘反思教学行为,而学生在后测练习中的完成情况则对本节课的教学效果起着评价作用。根据本节课的教学目标和教学重难点,笔者设计了一份后测练习,以期从中了解本次课堂教学行为存在的不足之处。
问题一的前3 个小题以及问题二的解答正确率高达92%,由此可知,学生对于“整体和部分的关系”以及“分数的意义”这两个知识点掌握得较好。问题一中第4 个小题的解答正确率偏低,也就是说,学生对于“一个计量单位可看作单位1”这一知识点还存在困惑。
问题三是动手操作题,重点考查学生对单位“1”的掌握情况。本题的解答正确率是62%,说明还有部分学生没弄清楚“爸爸吃的是以整个西瓜为单位‘1’,浩浩吃的是以半个西瓜为单位‘1’。当单位‘1’变化时,相应分数所对应的数量也在随之变化”。
问题四是变式思辨的练习,难度较大,逆向考查学生对分数的理解。本题学生的解答正确率较高,为84%,也就是说,学生通过本节课的学习,能深刻地把握分数的意义,达到了深度学习的效果。
教师要引导学生通过纵向比较,确定同一个知识要点的发展方向,聚焦萌发点与连接点,在有限的时间内抓住关键环节,促进学生深度学习。
