变形核中的晕现象与形状退耦合

孙向向 周善贵,3,4,5

1（中国科学院大学 核科学与技术学院 北京 100049）

2（中国科学院理论物理研究所 中国科学院理论物理前沿重点实验室 北京 100190）

3（中国科学院大学 物理学院 北京 100049）

4（湖南师范大学 量子效应及其应用协同创新中心 长沙 410081）

5（中国科学院理论物理研究所 北京航空航天大学彭桓武科教合作中心 北京 100191）

随着世界范围内放射性核束物理的快速发展，在远离β 稳定线的原子核中发现了很多奇特核现象，包括集团结构、中子晕和质子晕、中子皮，以及传统幻数的消失和新幻数的出现等［1-5］。对晕等奇特现象的研究是目前核物理的前沿领域。1985年，科学家们在11Li中首次观察到了原子核中的晕现象［6］，这项研究工作开启了奇特核研究的热潮。之后，人们在实验室先后发现了约20 例晕核［1］。近些年来，又先后发现了31Ne［7-8］、37Mg［9］、17，19B［10-11］和29F［12］等晕核。此外，也有一些工作结合实验结果和理论描述致力于解释晕的形成机制［9，13］。例如，通过单中子剔除反应和壳模型计算，Nakamura 等［9］揭示了31Ne 是变形的并且具有p-波导致的晕结构，31Ne 也是第一例实验上确定的变形晕核。虽然通过实验理论结合的方式已经解释了若干个晕核的性质，但大多数晕核的性质及其形成机制依然有待探索。最早发现的晕核11Li 是一个球形晕核［14］。但大多数开壳核都是变 形 的。很 多 晕 核（包 括17，19B、22C、29F、31，34，36Ne、37，42，44Mg）被证实或被预言是变形的［9-10，15-19］。特别是处于N= 20反转岛附近的晕核，例如29，31F和31Ne，其性质与壳演化、形变效应、连续谱以及这三者之间的耦合密切相关，亟须进一步深入研究。除此之外，在一些滴线原子核或者是晕核里观测到了激发态［1］。对包括晕核在内的弱束缚原子核低激发谱性质的研究，也是目前理论和实验核物理的前沿之一。

研究晕结构的理论方法主要有：晕有效场理论［20］、反对称分子动力学模型［21］、少体模型［22］、Gamow壳模型［23］、从头（abinitio）计算［24-25］以及密度泛函理论（Density Functional Theory，DFT）［26-29］。这些模型各具特色。其中。DFT 建立在原子核内禀系，基于全局的有效核子-核子相互作用，可以微观自洽地研究晕的形成机制，同时包含形变效应；但对激发谱的研究需要引入对称性恢复方法。DFT是描述原子核性质最成功的理论之一。早在1996年，孟杰和Ring 就在DFT 框架下，针对球形晕核，利用包含连续谱的相对论Hartree-Bogoliubov（Relativistic Continuum Hartree-Bogoliubov，RCHB）理论微观解释了11Li 中双中子晕结构［14］。利用RCHB 理论，也预言了Ca和Zr同位素链中的巨晕现象［30-31］。此外，文献［32-36］基于DFT研究了球形晕。变形晕核的微观自洽描述由形变的包含连续谱贡献的相对论Hartree-Bogoliubov（Deformed Relativistic Hartree-Bogoliubov in continuum，DRHBc）理论实现［17］。之后，采用非相对论DFT 也研究了变形晕的性质［28，37-39］。DRHBc 理论也预言了在变形晕核中，晕核的晕和核芯有不同的形状，这种奇特现象称之为形状退耦合［17］。

在上述基于密度泛函理论的研究中，大多数工作都是研究变形晕核的基态性质，少有工作去探索晕核的激发态特别是转动激发态性质。在密度泛函理论框架下，原子核谱学研究必须考虑从实验室系到内禀系的自发对称性破缺，包括U（1）对称性和SO（3）对称性。通常用粒子数投影和角动量投影去恢复破缺的U（1）和SO（3）对称性。另外，原子核是一个量子多体系统，其基态附近的集体自由度涨落需要用生成坐标方法处理。基于相对论或者非相对论平均场模型的超越平均场方法已经广泛地用于研究原子核的低激发谱［40-41］。基于相对平均场模型，这些超越平均场方法也用于研究具有轴对称形变［42-43］、三轴形变［44-45］、八极形变［46］以及更复杂形变［47］原子核的激发谱。但这些模型均在谐振子基空间求解，无法恰当地描述波函数在远离核心处的渐近行为，因此不适合于描述晕核。最近，基于DRHBc 理论，引入角动量投影，实现了变形晕核转动激发的微观自洽描述［48-49］。该模型可以自洽地给出变形晕核基态以及低激发态的性质。本文将总结近十余年来基于DRHBc 理论研究变形晕核的一些进展。

1 DRHBc理论和角动量投影

DRHBc 理论基于介子交换的或者点耦合的核子-核子有效相互作用［18，50-51］，忽略核子之间的交换作用（Hartree 近似），并用Bogoliubov 变换处理由对关联诱导的连续谱贡献，体系的准粒子波函数由Dirac-Hartree-Bogoliubov（DHB）方程给出。对于晕核，由于其价核子波函数在空间上可以延伸到远离核心的位置，对晕核的描述需要恰当地处理这样的渐近行为。对于球形晕核，可以直接在一维坐标空间 采 用 打 靶（shooting）法［26］、有 限 元 方 法［52］、Lagrange-mesh 法［53］等方法求解DHB 方程。但是对于轴对称变形原子核，在坐标空间直接求解DHB方程数值上比较困难。可以用基展开的方法去求解，通常采用的完备基包括谐振子基［54］、Dirac Woods-Saxon（DWS）基［55］或者变换后的谐振子基［56］。在DRHBc 理论中，采用DWS基去求解变形的DHB方程。与谐振子基相比，DWS基的优势在于它可以保证弱束缚轨道波函数的渐近行为。在DWS基中，可以通过对角化变形体系的DHB 矩阵来得到准粒子波函数和相应的准粒子能量。利用准粒子波函数，可以计算系统基态性质，包括能量、半径、密度分布等，进而与实验比较或者预言奇特原子核的性质［18］。

DRHBc 理论只能给出原子核在本体系下的基态性质，无法用于研究激发态性质。这是由于，对于变形原子核，实验室系下的SO（3）对称性在本体系下自发破缺。需要把破缺的SO（3）对称性恢复后，才能描述原子核的激发态。在密度泛函框架中，通常采用角动量投影技术去恢复SO（3）对称性。为了研究晕核这类弱束缚原子核的激发态性质，我们在DRHBc 理论基础上以变分后投影的方式实现了角动量投影［48-49］。值得一提的是，之前密度泛函理论框架下的几乎所有超越平均场计算都是基于谐振子基实现，在DRHBc 理论基础上，我们实现了基于DWS基的超越平均场计算。作为孤立体系，原子核的角动量是好量子数。然而，由于对称性自发破缺，本体系下的平均场波函数是具有不同角动量波函数的叠加。通过角动量投影技术，便可以把具有确定角动量（好量子数）的态投影出来，给出原子核的基态和低激发谱。

2 变形晕结构以及变形晕核的转动激发

本节主要介绍DRHBc理论对硼、碳和镁同位素链中晕核的描述以及超越平均场方法对变形晕核激发态的研究。在DRHBc 理论研究不同质量区的原子核时，数值条件可能略有不同。在绝大部分计算中［15，17-19，57-58］，采用密度依赖的零程对力，其对应的准粒子空间的能量截断是60 MeV。对力强度通常通过拟合实验对能隙或者是原子核质量的奇偶差决定。数值求解DWS基波函数时［59］，径向坐标截断到20 fm，步长为0.1 fm。单粒子DWS基的角动量截断为21/2ℏ。费米海中单粒子DWS 基的能量截断为100 MeV，狄拉克海中的DWS基波函数的数目与费米海中的数目保持一致。经检验，这样的数值条件在计算轻质量原子核的性质时能达到恰当的精度。

2.1 镁同位素链中的变形晕

DRHBc 理论的一个重要应用是研究镁同位素链中的变形晕结构。利用NL3 有效相互作用［60］，DRHBc预言了在丰中子镁同位素中，46Mg是该同位素链的中子滴线原子核［17］，44Mg 是一个变形晕核。44Mg 的双中子分离能S2n非常小，只有0.44 MeV，四极形变参数β2为0.32，也即基态呈长椭形变。图1（a）展示了44Mg 的质子、中子二维密度分布，z轴是对称轴，红点表示圆形。44Mg 是一个弱束缚的极端丰中子原子核，所以其中子密度比质子密度在空间上延展得更远。在平均场模型中，分析价中子的轨道成分可以给出晕核的组态以及晕的形成机制。图2 展示了44Mg 在正则基中邻近中子费米能级（λn）的中子单粒子能级图。每条能级用角动量z-分量Ω和宇称π 标记，横线长度正比于该能级上中子的占据数。n表示能级次序。在图右侧，给出了一些能级的主要球形DWS 基分量。短划线代表利用BCS 公式和平均对能隙求得的占据数。在中子费米能级以下，价中子占据弱束缚的3/2-、1/2-能级，在费米面以上的连续谱中，也有部分占据的能级。通常，晕核的形成是由于弱束缚的或者是处于连续谱的低轨道角动量（s或者是p波）波函数导致的。在44Mg 的价核子波函数中，能级n=3，4，6中有p波贡献并且p波轨道的核子占有数约为2，这导致了该原子核的晕结构。

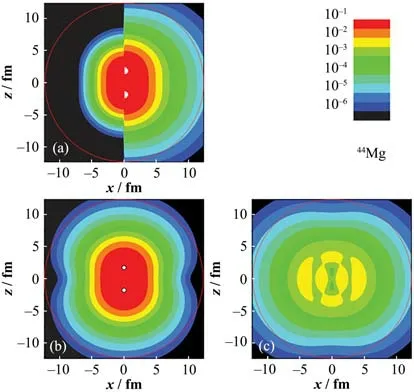
图1 44Mg的二维密度分布图[17](a) x<0的区域对应质子密度，x>0的区域是中子密度，(b) 对应中子核芯的密度，(c) 对应中子晕的密度分布Fig.1 Density distributions of 44Mg[17](a) The proton (x<0) and the neutron (x>0) densities, (b) The density of the neutron core, (c) The density of the neutron halo

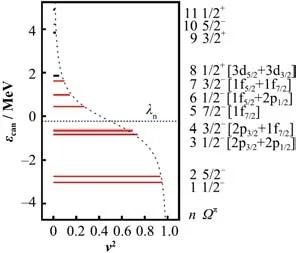
图2 44Mg的正则基中的中子单粒子能级图[17]Fig.2 Single neutron levels of 44Mg in the canonical basis[17]

根据中子的能级结构，可以把中子对密度的贡献分成两个部分：能级1和2及能量更低的能级上的中子形成中子的核芯；能级3 及能量更高的能级上占据的中子则形成中子晕。根据这样的划分，所有中子的密度也可以分为中子核芯和中子晕两部分。这两部分的二维密度分布见图1（b）和（c），可见，中子核芯的形状具有长椭形变，而中子晕则呈扁椭形变。因此，变形晕核中晕和核芯可以有不同的形变，这个现象被称为变形晕核中的“形状退耦合”。核芯和晕的形状源于内禀波函数的性质。就44Mg 的中子晕而言，p波轨道的空间角分布包含球谐函数Y10（θ）和Y1±1（θ）的贡献，其中，前者呈长椭形状而后者呈扁椭形状。在44Mg 的价核子波函数中，Y1±1（θ）的成分更大，所以该原子核的中子晕为扁椭形状。

在DRHBc理论对镁同位素的描述中，42Mg也是一个变形的双中子晕核［18，58］，它的晕结构是由弱束缚的价核子轨道中含有p波成分导致的。但目前，实验上观测到最重的镁同位素是40Mg，因此42，44Mg中的变形晕依然有待实验验证。在40Mg 中是否含有变形晕结构，依然是一个开放性问题。DRHBc理论预言40Mg不是一个变形晕核。在镁同位素中，实验上已经观测到37Mg的单中子晕［9］。利用考虑奇核子堵塞效应和奇时间场贡献的DRHBc 理论研究表明，37Mg是一个变形的单中子晕核［61］。

2.2 硼和碳同位素链中的变形晕结构

在硼和碳同位素链中，实验观测表明，在17B、19B、15C、19C 和22C 中有中子晕，这些原子核中晕的形成机制和性质以及是否存在变形晕等问题依然是未解决的。本节简要给出利用DRHBc 理论对这些晕核的描述。表1 给出了针对这些原子核，DRHBc 理论计算的形变值、中子分离能、核物质半径，并与已有的实验结果进行了比较。结果表明，DRHBc理论计算与实验符合较好。

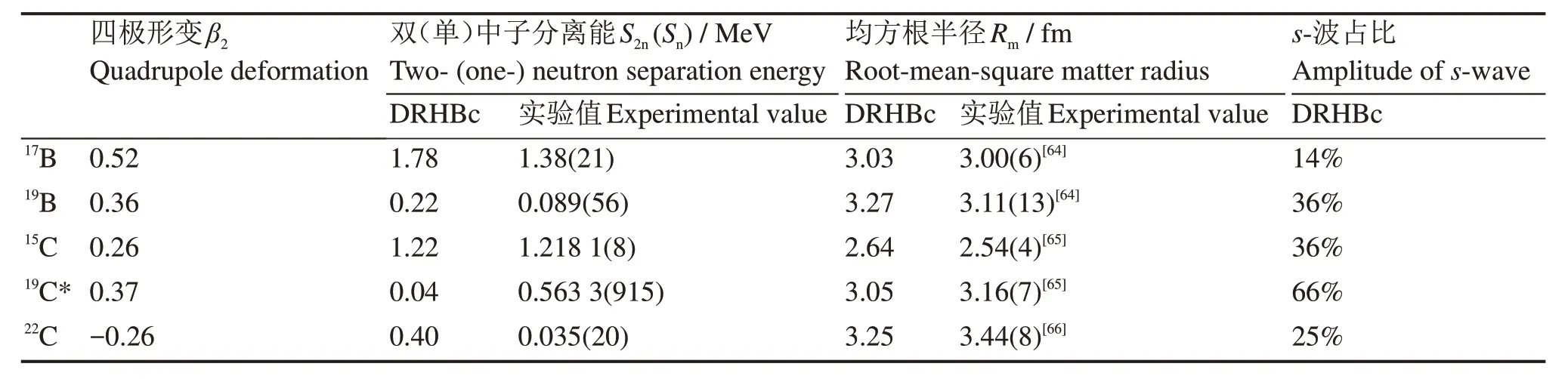
表1 采用PK1密度泛函[62]进行DRHBc理论计算得到的硼和碳同位链中晕核性质（四极形变值、双中子晕核的双中子分离能、单中子晕核的单中子分离能、均方根半径、s波轨道占比）以及与实验的比较。中子分离能的实验值来自AME2020[63]Table 1 Quadrupole deformation parameter, two- or one- neutron separation energy, root-mean-square matter radius, and the amplitude of s-wave components of the halo nuclei in born and carbon isotopes from the DRHBc calculations with the density functional PK1[62]. Available experimental values are included for comparison. The experimental data of neutronseparation energies are taken from AME2020[63]

在硼同位素链中，DRHBc 理论预言17B 和19B 都存在变形晕［10，15］，晕中子部分占据s轨道。其中，实验上通过中子剔除反应得到17B 的两个价中子中，s-波的成分只有9（2）%。这也是目前实验上发现的低角动量轨道占比最小的晕核。基于变形晕机制，DRHBc 理论计算表明该原子核是变形核，s-波占比为14%。DRHBc 理论得到的中子分离能和半径也与实验较为符合。2020年，实验上在库仑破裂反应中测量到的19B 的B（E1）激发谱表明该原子核有中子晕，但是其晕结构和形成机制有待进一步探索［11］。假设双中子分离能为0.5 MeV，三体模型的计算结果表明19B是一个由s-波导致的双中子晕核，其占比为35%。DRHBc理论的计算表明19B是一个变形的双中子晕核，s-波占比与三体模型计算一致［15］。除此之外，双中子晕核17，19B 都有形状退耦合现象：长椭形状的中子核芯以及扁椭形状的中子晕。

DRHBc理论预言在碳同位素链中，15，22C基态都存在变形晕结构［19，57］。15C基态呈长椭形状并具有s-波单中子晕核。其中子核芯是近球形而中子晕是长椭形状，这表明在单中子晕核中，也存在形状退耦合这一奇特核结构。最近，基于含时密度泛函的计算表明15C 的变形晕结构导致熔合反应15C+232Th 库仑位垒以下截面的增强［67］。对于22C，目前实验上仅有半径的数据和破裂反应中核芯的动量分布测量结果，尚未有B（E1）跃迁的相关实验结果。DRHBc理论计算揭示出22C中可能存在多种奇特核现象，包括形变晕（“收缩晕”）、单粒子能级反转导致的壳结构变化、形状退耦等，解释了该原子核的双中子分离能、半径和组态相关的疑难［19，57］。对于19C，DRHBc计算给出的基态呈扁椭球形，没有中子晕。自旋宇称是3/2+，与实验值1/2+不符。但在DRHBc计算中，19C 的长椭形变的同核异能态（标记为19C*）的自旋宇称是1/2+，并且具有单中子晕结构。

DRHBc 理论除了预言和探索变形晕的基态性质外，还被用于研究经典禁区之外的粒子数以表征晕结构［58］、探索滴线外束缚的原子核［68-70］、重核中的形状共存和气泡结构［71-72］等。质量是原子核最基本的性质之一。最近基于DRHBc理论，正在构建高精度的、同时包含形变和连续谱效应的原子核质量表［51，73-74］。此外，夏学伟等［75］基于点耦合密度泛函，利用DWS基展开方法，求解了偶偶核的包含固定对能隙的三轴相对论Hartree-Bogoliubov 方程。张开元等［76］分别基于点耦合和介子交换密度泛函，采用密度依赖的零程对力，考虑奇核子的堵塞效应，发展了三轴相对论连续谱Hartree-Bogoliubov 理论并探索了三轴形变对晕核性质的影响。DRHBc 理论中不包含核子交换相互作用，耿晶等人引入Fock 项，发展了包含连续谱贡献的形变相对论Hartree-Fock-Bogoliubov理论［77］。

2.3 变形晕核的转动激发

变形晕核是否有激发态？如果有，其激发模式是什么？有什么性质？这些都是变形晕核研究中的热点问题。在以上的讨论中，仅研究了变形晕核基态的性质。在DRHBc 理论基础上发展角动量投影方法，便可以去探索变形晕核转动激发的性质［48-49，78］。基于DRHBc 理论计算得到的44Mg 本征系波函数，通过角动量投影可以得到激发态波函数，进而研究激发态性质。计算表明，基于变形的44Mg基态波函数得到的激发谱符合原子核转动激发的规律，即激发能与角动量的平方呈线性关系。求解单体密度算符在投影波函数下的期望值，便可以得到激发态的密度分布。对于单体密度算符，在本征系所引入的中子核芯和晕的划分依然可以应用在投影激发态中。图3展示了0+、2+和4+态的中子晕、中子核芯以及中子的密度分布。对于0+态，原子核的密度分布呈球形，因此中子晕和核芯密度都是球形。在2+和4+态中，晕结构依然存在，核芯和晕的形状退耦合得到保持。究其根本，在原子核转动激发中，单粒子组态几乎没有改变，导致本体系中的内禀性质依然在转动激发态中得以保持。因此，在本体系中存在的变形晕结构和形状退耦合，在其低激发转动态中依然保持。这个预言有待实验验证。

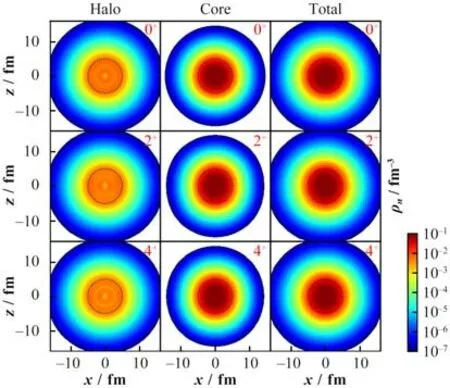
图3 DRHBc角动量投影计算得到的44Mg的0+、2+和4+态的中子晕、中子核芯以及所有中子的密度分布Fig.3 Neutron halo, neutron core, and neutron density distributions of 0+, 2+, and 4+ states of 44Mg by using the DRHBc theory with angular momentum projection

3 总结与展望

本文总结了基于协变密度泛函理论对变形晕核的描述。DRHBc理论通过自洽包含形变效应、连续谱贡献可以给出在本体系下变形晕核的结构和性质。利用DRHBc 理论：1）预言了42，44Mg 中p波导致的变形晕核，这个结论尚待实验验证；2）基于变形晕机制解释了硼同位素17，19B 中发现的晕现象；3）15，22C的晕结构可以用DRHBc理论解释，特别地，DRHBc计算表明，22C中晕的性质与壳结构和变形效应密切相关。此外，上述晕核中都存在晕与核芯的形状退耦合。基于DRHBc理论发展的超越平均场方法，可以用于探索变形晕的激发态性质。角动量投影的计算表明，本体系中存在的晕结构在转动激发态中依然得以保持。

晕核的性质与原子核的形状密度相关。目前基于DRHBc理论，可以研究反射对称形变的轴对称和三轴形变原子核，但是还没有考虑反射不对称形变。因此有必要将DRHBc 理论扩展到发展包含反射不对称形变。因为超子不需遵从核子的泡利不相容原理，可以利用超子作为“探针”去探测原子核的性质，例如探索超子对变形晕核性质的影响。这需要在DRHBc 理论基础上考虑超子自由度。在基于DRHBc理论的超越平均场计算中，目前只包括了角动量投影。加入粒子数投影考虑粒子数涨落的影响以及用生成坐标方法处理集体自由度的涨落，以实现变形晕核基态到激发态的微观自洽描述，也是今后工作的主要目标。

作者贡献声明孙向向负责文章起草撰写、修改以及文章资料的查阅及整理；周善贵负责文章框架、整体把握和最终版本的修订。