同位旋标量对力对42Ca中自旋-同位旋跃迁的影响
2023-08-31牛一斐
郭 亮 牛一斐
1(兰州大学 核科学与技术学院 兰州 730000)
2(兰州大学 稀有同位素前沿科学中心 兰州 730000)
在多体关联体系中,配对是一种普遍存在的现象。对于由质子和中子通过强相互作用[1-2]组成的原子核体系,核子之间的对相互作用可分为同位旋矢量(T= 1)与同位旋标量(T= 0)道。同位旋矢量对相互作用存在于质子-质子、中子-中子与质子-中子之间,其中,质子-质子与中子-中子间的对相互作用[3]对开壳核大块性质的描述[4-5]以及弱束缚体系的形成[6-8]十分重要。由于核力[9]的电荷无关性,同位旋矢量的质子-中子对力应等于质子-质子或中子-中子之间的对力[10]。同位旋标量对相互作用则仅存在于质子-中子之间,目前实验上还没有能够直接联系同位旋标量对力的可观测量。对于质子数与中子数不相等(N≠Z)的体系,由于质子与中子的费米面位于不同的单粒子轨道,原子核基态的质子-中子对力通常不起作用。然而,对于原子核的自旋-同位旋激发,即使对于N≠Z的体系,也需要考虑质子-中子对相互作用[10]。
原子核的自旋-同位旋激发可以对核力信息提供有效限制。原子核自旋-同位旋激发的主要模式包括伽莫夫-泰勒(Gamow-Teller,GT)激发和自旋-偶极(Spin-dipole,SD)激发。实验上,Fujita 等[11-12]通过电荷交换实验42Ca→42Sc 发现,其GT 跃迁的大部分跃迁强度集中在42Sc 位于0.6 MeV 的最低激发态,从而发现了低能量GT 声子激发的存在。这反映了42Ca 中SU(4)对称性的恢复,这一低能量激发态被称为超级GT 态。为了解释这一实验现象,Bai等[13]利用自洽的Skyrme Hartree-Fock-Bogoliubov+准粒子无规相位近似(SHFB+QRPA(Quasi-particle Random Phase Approximation))模型进行计算,表明了同位旋标量对力的引入能够重现42Sc中低能量超级GT 态。Sun 等[14]通过大规模壳模型计算也得出了相同的结论,即同位旋标量对力对于42Sc 中态的形成十分重要。对于原子核中的SD跃迁,同位旋标量对力的研究尚十分缺乏。Yoshida 等[15]采用三体模型研究了零程同位旋标量对力对SD 跃迁强度分布的影响,表明同位旋标量对力对于SD跃迁中具有较高轨道角动量且主量子数相同的组态影响较大。
无规相位近似(Random Phase Approximation,RPA)理论可以研究核素图上除少数轻核之外的所有原子核,被广泛应用于原子核集体激发的研究。在RPA理论中,模型的自洽性要求采用同一个能量密度泛函对原子核的基态和激发态进行描述。自洽性是恢复被平均场近似破坏的对称性、去除物理激发态中的假态以及将理论结果外推到实验未知区域的关键[16-17]。根据不同的密度泛函,RPA 理论可分为非相对论RPA[18-21]和相对论RPA[22-24]。协变密度泛函理论对于原子核的基态和激发态的研究都取得了巨大的成功[25-29]。基于相对论Hartree-Bogoliubov(RHB)或相对论Hartree-Fock-Bogoliubov(RHFB)模型,建立了质子-中子QRPA模型[30-31],并探讨了同位旋标量对力对GT 跃迁[30-33]与β 衰变的影响[32-35]。然而,同位旋标量对力对SD 跃迁的影响以及N≈Z原子核中的低能量超级GT 态尚未被研究。因此,本文将利用RHB+QRPA 模型研究同位旋标量对力对42Ca中β-方向的GT(GT-)跃迁和SD(SD-)跃迁的影响。
1 理论框架
1.1 QRPA方程
相对论的QRPA 方程可以由时间依赖的RHB模型通过小振幅近似得到[23],其等价于线性Bethe-Salpeter 方程[17]。线性Bethe-Salpeter 方程在动量空间或坐标空间为积分方程。由于QRPA方程一般写在正则单粒子基空间,此时积分变为了对正则基指标的求和。对于球形偶偶核,角动量耦合形式的质子-中子相对论QRPA(PNQRPA)方程可写为:
矩阵AJ和BJ的矩阵元在正则基下的表达式为
其中:p和n分别表示正则基下的质子态和中子态;up,n和vp,n为正则基下单粒子轨道的非占据与占据振幅;Hpp'和Hnn'由单核子哈密顿量hD以及对场Δ组成,其形式为(κκ'=pp'或者nn')。
为了保证QRPA 模型的完备性,其组态空间不仅考虑了来自费米海中的质子-中子对,还包含了由费米海中完全占据或部分占据态与狄拉克海中的负能态所组成的质子-中子对。狄拉克海中负能态的组态的考虑对于Ikeda 求和规则的满足十分重要[36,30]。在PNQRPA方程(1)中,Eν为激发态|νJ的本征能量,而和则为激发态|νJ的两准粒子跃迁振幅。矩阵AJ和BJ中的为质子和中子之间的粒子-空穴剩余相互作用矩阵元,由单粒子哈密顿量对质子中子密度ρpn求导得到。在RHB计算中,当不包含Fock 项时,由于宇称守恒,π 介子的贡献为0。然而对于自旋自由度相关的激发,π介子的贡献十分重要,因此被包含在QRPA 计算中。为了消除由于引入π 介子产生的发散项,需引入零程的Landau-Migdal 项,其强度g'为自由参数,可以通过重现208Pb 的GT 共振能量来确定。对于相互作用DD-ME2[37],g'= 0.52。为质子和中子之间的粒子-粒子剩余相互作用矩阵元。对于同位旋矢量道(T= 1),采用了与RHB 模型中相同的对相互作用形式,即Gogny对力,选取的参数组为D1S[38]。对于同位旋标量道(T= 0),我们采用了高斯型对相互作用[10]:
其中:μ1=1.2fm,μ2=0.7fm,g1= 1,g2=-2。S=1,T=0为投影到具有量子数S=1和T=0的质子-中子耦合态的投影算符;V0表示同位旋标量对力的强度。由于正则单粒子波函数一般写在坐标空间,故剩余相互作用矩阵元的计算需要对坐标进行积分,该积分由径向积分与角向积分的乘积所组成。
1.2 跃迁强度
通过求解QRPA 方程(1),可将由β-方向的自旋-同位旋算符所引发的跃迁强度表示为:
为了得到连续的响应函数R(E),我们可以引入洛伦兹函数平滑分离的跃迁强度Bν:
式中:Γ为平滑宽度,在计算中取为1 MeV。对于β-方向的跃迁,可以定义某一组态对应的跃迁振幅[13]:
对于给定的原子核激发态,该跃迁振幅可以用来评估其中某一质子-中子组态的贡献。
对于GT-跃迁和SD-跃迁,相应的自旋-同位旋算符分别为[39-40]:
2 结果和讨论
利用QRPA模型,我们计算得到了42Ca中GT跃迁和SD 跃迁强度分布。对于基态RHB 方程的求解,我们采用了球谐振子基,并将谐振子的主壳层数取为20。在QRPA 模型中,对于来自Fermi 海和Dirac 海的组态的能量截断分别取为200 MeV 和2 000 MeV,占据因子乘积upvn或者unvp的最低截断取为0.01。
2.1 GT跃迁
图1 给出了不同同位旋标量对力强度下42Ca 中GT-跃迁的强度分布。该结果由RHB+QRPA模型计算得到,采用的相互作用为DD-ME2,同位旋标量对力强度分别取为V0=0 MeV, 100 MeV, 200 MeV,250 MeV。当同位旋标量对力强度取为0时,出现了两个GT 激发态,分别位于能量8.12 MeV 和15.46 MeV,在图中分别标记为A和B。当同位旋标量对力的强度取为100 MeV 时,出现了位于能量13.62 MeV 的GT 激发态,标记为C,此时,激发态B的强度明显下降,而激发态A的强度则有所上升,且其激发能向低能量处移动。随着同位旋标量对力强度继续增加到200 MeV,GT激发态A的强度进一步上升,其激发能也朝着更低能量处移动。对于GT激发态C,其强度出现了下降现象,并且其激发能也随之降低。而对于激发态B,其强度和激发能的变化都很小。当同位旋标量对力强度增强到250 MeV时,激发态A的强度继续上升,其激发能也继续朝着更低能量处移动,而激发态C 几乎消失不见。图1中同时给出了实验上发现的低能量超级GT态[11-12]。当同位旋标量对力强度取为200 MeV 时,GT-态的强度主要集中于激发态A处,与实验符合较好,这表明同位旋标量对力的引入可以重现实验上的低能量超级GT 态,从而恢复42Ca 中SU(4)对称性。然而,此时的能量相比于实验过低,这可能是由于粒子-空穴道相互作用选取的原因。
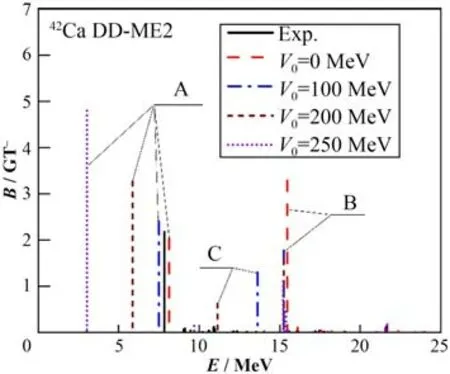
图1 基于RHB+QRPA模型,采用DD-ME2相互作用得到的42Ca的GT-跃迁强度分布与实验[7-8]的比较Fig.1 GT- strength distributions in 42Ca obtained via RHB+QRPA calculations for the DD-ME2 interaction in comparison with experimental results[7-8]
为了理解42Ca 中GT-跃迁强度分布随着同位旋标量对力强度的演化行为,我们对各激发态的组态进行了分析。在图1中,GT激发态A、B、C的主要两准粒子组态分别为(ν1f72,π1f72)、(ν1f72,π1f52)和(ν1f52,π1f72)。根据式(2),粒子-空穴剩余相互作用与粒子-粒子剩余相互作用部分的贡献分别与矩阵AJ中 系 数 cfph=vpunvp'un'+upvnup'vn'和cfpp=upunup'un'+vpvnvp'vn'的大小有关。表1 给出了由组态(ν1f72,π1f72)、(ν1f72,π1f52)和(ν1f52,π1f72)组成的pnp'n'两体矩阵元的系数cfph 和cfpp。从表1 中可以看出,GT 激发态C 的主要两准粒子组态(ν1f52,π1f72)相关的剩余相互作用矩阵元系数cfpp远大于cfph,这表明该组态主要受粒子-粒子剩余相互作用的影响,而受粒子-空穴剩余相互作用的影响较小。当不考虑同位旋标量对力时,即V0=0 MeV,组态(ν1f52,π1f72)相关的QRPA矩阵非对角元很小,因此,该组态与其他组态不发生混合。由于该组态对应的占据因子乘积upvn仅为0.08,故该组态贡献的跃迁强度很小,GT 激发态C 的跃迁强度几乎为0。
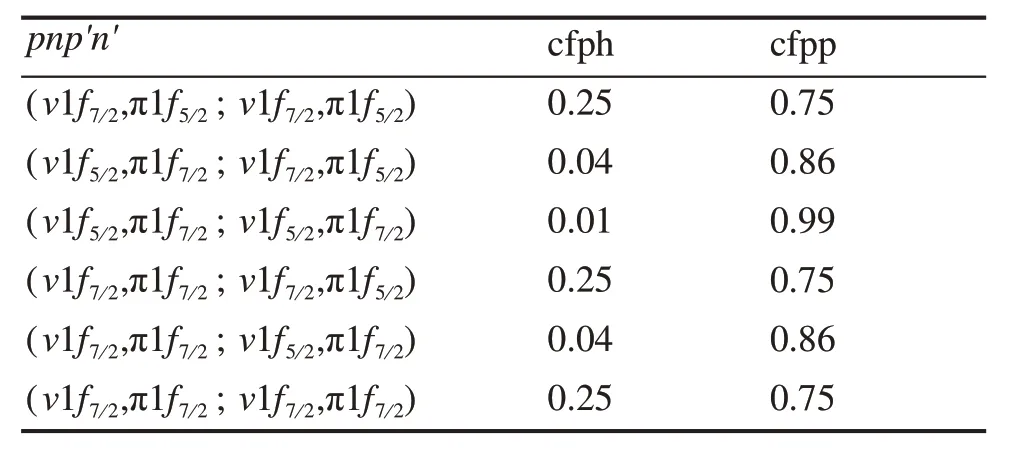
表1 基于RHB+QRPA模型,采用DD-ME2相互作用得到的剩余相互作用矩阵元对应的系数cfph和cfppTable 1 Coefficients cfph and cfpp in front of the residual interaction matrix elements obtained using the RHB+QRPA model for the DD-ME2 interaction
当V0=100 MeV 时,两准粒子组态(ν1f52,π1f72)相关的QRPA矩阵非对角元增大,使得GT激发态C的主要组分(ν1f52,π1f72)与激发态B 的主要组分(ν1f72,π1f52)构成的QRPA矩阵非对角元增大,导致激发态C 与B 的组分发生相互混合,从而激发态C的跃迁强度增加,激发态B的跃迁强度降低。同时,同位旋标量对力的增强也会使得GT 激发态A 的主要组分(ν1f72,π1f72)与GT 激发态B 的主要组分(ν1f72,π1f52)构成的QRPA矩阵非对角元增大,从而使激发态A 与B 的组分发生相互混合,导致激发态A 的跃迁强度增加。此外,由于同位旋标量对力的吸引性质,其贡献的粒子-粒子剩余相互作用矩阵的对角元小于0,使得激发态A 和B 朝着低能量处移动。然而,对于激发态B,由组态(ν1f72,π1f52)和组态(ν1f52,π1f72)构成的QRPA 矩阵非对角元大于0,抵消了大部分QRPA 矩阵对角元的减小,因此激发态B的能量移动很小。
当同位旋标量对力增强到200 MeV 时,激发态A中组态(ν1f72,π1f52)的混合占比继续增大,其激发强度也进一步增强。粒子-粒子剩余相互作用矩阵元进一步减小,激发态A 的激发能也进一步降低。同时,激发态C 中进一步混入了激发态A 的主要组态(ν1f72,π1f72),由于该组态贡献的跃迁振幅与激发态B 的主要组分(ν1f72,π1f52)贡献的跃迁振幅相位相反,从而使得态C 的跃迁强度降低。而同位旋标量对力的吸引性质同样会使得激发态C 的激发能降低。
当同位旋标量对力强度增强到250 MeV 时,由于相同的原因,态A的跃迁强度变得更强,态C的跃迁强度变得更小,他们的激发能也变得更低。
为了考察模型相关性,我们还采用了相对论点耦合相互作用PC-PK1 进行了同样的计算,其结果表明,同位旋标量对力对42Ca中GT态的影响与DDME2相互作用是一致的。而两者的区别在于42Ca中GT 态的高能峰与低能峰的激发能量和跃迁强度不一样,这与剩余相互作用矩阵元的模型依赖性有关。
2.2 SD跃迁
为了研究同位旋标量对力对42Ca 中SD-跃迁的影响,图2 给出了0-、1-和2-跃迁在不同同位旋标量对力强度下的强度分布。该结果同样由RHB+QRPA模型计算得到,并采用了DD-ME2相互作用,同位旋标量对力强度分别取为0 MeV、150 MeV、300 MeV 和500 MeV。可以看出,随着同位旋标量对力强度的增强,0-、1-和2-跃迁的强度分布变化较小。这是因为42Ca 中SD-主要跃迁组态所构成的粒子-粒子剩余相互作用矩阵元都比较小,因此,当改变同位旋标量对力强度时,QRPA 矩阵元的变化很小,从而导致最终SD-跃迁中各峰的强度以及激发能的变化不大。其中,0-和1-跃迁中主峰的主要组态为(ν1d52,π1f52),而2-跃迁中主峰的主要组态为(ν1d52,π1f72)。此外,当同位旋标量对力强度非常大,取为500 MeV时,0-和1-跃迁中才会发生一定程度的组分混合,导致低能区出现了新的低强度小峰。其中0-跃迁中该峰的主要组分为(ν1f72,π2g72),1-跃迁中该峰的主要组分为(ν1f72,π1g72) 和(ν1f72,π2g92)。
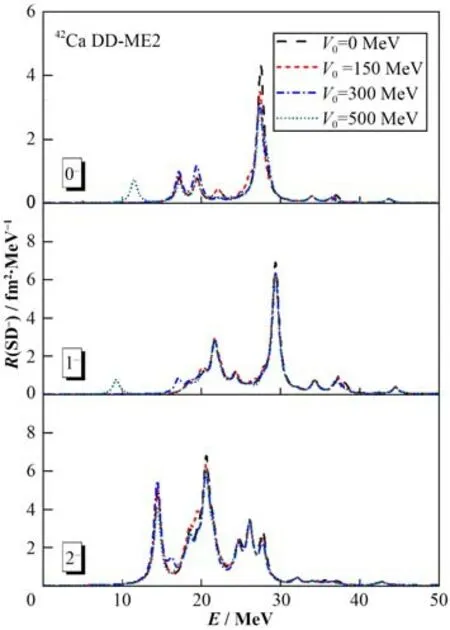
图2 基于RHB+QRPA模型,采用DD-ME2相互作用得到的42Ca中SD-跃迁强度分布Fig.2 SD- strength distributions in 42Ca obtained via RHB+QRPA calculations for the DD-ME2 interaction
3 结语
本文利用RHB+QRPA 模型研究了高斯型同位旋标量对力对42Ca 中GT-跃迁和SD-跃迁的影响。对于GT-跃迁,同位旋标量对力的增强会使得不同GT激发态的主要组分之间发生混合,从而导致低能峰的增强和高能峰的降低。由于同位旋标量对力的吸引特性,使得GT-跃迁强度分布朝着低激发能方向移动,其中由组态(ν1f72,π1f72) 和组态(ν1f52,π1f72)所主导的GT激发态的移动比较明显。当同位旋标量对力强度为200 MeV 时,GT-跃迁与实验得到了较好的符合,从而证实了同位旋标量对力对于恢复SU(4)对称性的重要作用。对于SD-跃迁,由于0-、1-和2-跃迁中各峰的主要组态所构成的粒子-粒子剩余相互作用矩阵元都比较小,同位旋标量对力强度的改变并不会引起SD-跃迁强度的分布的显著变化。
作者贡献声明郭亮完成理论计算并撰写了论文第一稿;牛一斐审阅修改论文。
